Similar presentations:
Корреляционный анализ. Оценка коэффициента корреляции
1.
Основыкорреляционного анализа
2.
Многие объекты исследования характеризуются неодним, а множеством параметров, которые формируются
в виде матрицы:
X n k
x11
...
xi1
...
x
n1
... x1 j
... ...
... xij
... ...
... xnj
хij – i-ое наблюдение j-ого фактора.
... x1k
... ...
... xik
... ... , где
... xnk
3.
Основная задача – выявление взаимосвязимежду случайными переменными.
Задачи:
отбор факторов, оказывающих наиболее
существенное влияние на результативный
признак;
обнаружение ранее неизвестных причинных
связей.
Основные средства анализа данных:
парные коэффициенты корреляции,
частные коэффициенты корреляции и
множественные коэффициенты корреляции.
4.
Парный корреляционный анализ5.
Если X и Y − СВ, то теоретическая ковариация :cov( X , Y ) M ( X M ( X ))(Y M (Y ))
Если X и Y − независимы, то cov( X , Y ) 0 .
Выборочная ковариация – статистическая
взаимосвязи двух переменных.
При наличии n наблюдений:
мера
1 n
cov( X , Y ) ( xi x )( yi y ) , где
n i 1
( x1 , y1 ), ( x2 , y2 ),...,( xn , yn ) – фактические значения X и Y,
1 n
y yi .
n i 1
1 n
x xi .
n i 1
cov( X , Y ) xy x y .
6.
Коэффициент парной корреляциии проверка его значимости
Для X и Y теоретический коэффициент корреляции:
ρx,y
cov( X , Y )
2
x
2
y
cov( X , Y )
x y , где
x 2 , y 2 - дисперсии СВ X и Y, cov( X , Y ) – их ковариация.
Свойства:
1. 1 ρx,y 1 .
2. При ρxy=±1 СВ X и Y связаны линейной
зависимостью, т.е. Y=αX+β.
связь
корреляционная
линейная
ρxy=0
3. При
отсутствует.
7.
Оценка коэффициента корреляции – выборочныйпарный коэффициент корреляции r:
n
cov( X , Y )
r
Sx S y
r
( x x )( y
i 1
i
n
n
i 1
i 1
i
y)
2
2
или
)
y
y
(
)
x
x
(
i
i
xy x y
x x y y ,где
2
2
2
2
n
n
1
1
2
2
2
2
S
(
y
y
)
S x ( xi x )
y
i
,
n i 1
n i 1
дисперсии величин X и Y.
– выборочные
8.
Оценка тесноты связи можно переменнымиВеличина коэффициента корреляции
при наличии
Теснота связи
прямой связи (+) обратной связи (−)
Связь отсутствует
r 0
r 0
Связь очень слабая
0 r 0,3
0,3 r 0
Связь слабая
0,3 r 0,5
0,5 r 0,3
Связь средняя
0,5 r 0,7
0,7 r 0,5
Связь сильная
0,7 r 0,9
0,9 r 0,7
0,9 r 1
1 r 0,9
r 1
r 1
Связь очень сильная
Полная функциональная
9.
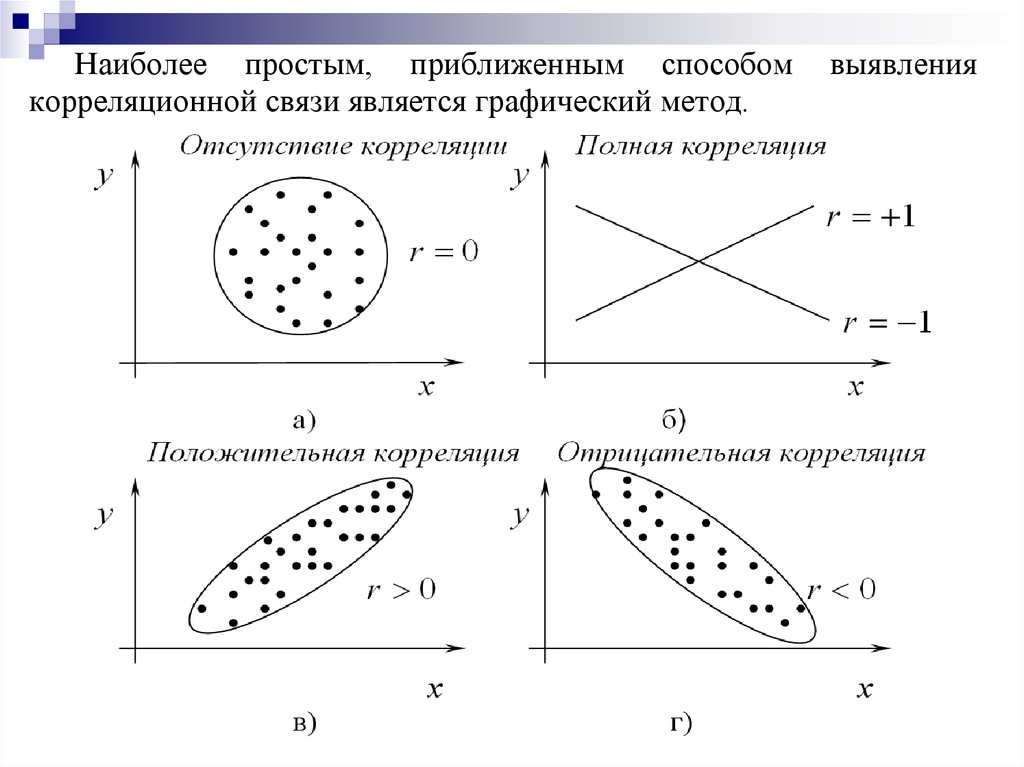
Наиболее простым, приближенным способомкорреляционной связи является графический метод.
выявления
10.
ОЦЕНКА ЗНАЧИМОСТИ КОЭФФИЦИЕНТА ПАРНОЙКОРРЕЛЯЦИИ
H 0 : 0 – значение коэффициента корреляции для
генеральной совокупности равно нулю, т.е. в генеральной
совокупности отсутствует корреляция.
H1 : 0 .
Оценка значимости осуществляется с помощью tкритерия Стьюдента:
r
n 2
t набл
r
Sr
1 r 2 , где
1 r 2
Sr
n 2 – ошибка коэффициента корреляции.
11.
Строится двусторонняя критическая область, границыкритической области которой находят из условия:
P tнабл t
P tнабл t
.
,n 2
,n 2
2
2
2
tнабл сравнивается с tкр ; для двусторонней
критической области, которое берется с учетом
заданного уровня значимости α и числа степеней свободы
n 2 (функция Excel СТЮДРАСПОБР (α; n 2 )).
Если tнабл tкр , v n 2 , то полученное значение
коэффициента корреляции признается значимым (т.е. Н0
отвергается).
Вывод: с доверительной вероятностью γ=1–α можно
утверждать, что между исследуемыми переменными есть
линейная статистическая зависимость.
12.
КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕИ ПРОВЕРКА ЕГО ЗНАЧИМОСТИ
В случае нелинейной зависимости тесноту связи между
величинами оценивают по величине корреляционного
отношения:
n
1
2
ˆ
(
y
y
)
i i
i 1
n
2 , 0 1 , где
(
y
y
)
i
i 1
yi – наблюдаемые значения,
yˆ i – расчетные значения результативной переменной.
Величина
η2 ,
называемая
коэффициентом
детерминации, показывает, какая часть общей вариации Y
обусловлена вариацией Х.
13.
H 0 : 0– в генеральной совокупности отсутствует
корреляция.
H1 : 0 .
Для проверки гипотезы вычисляется статистика:
2 (n k )
F
~ F ( , 1 k 1, 2 n k )
2
, где
(1 )( k 1)
k – число факторов, n – количество наблюдений).
Строится критическая область ( Fкр, ; ) , для этого границы
критической области находят из условия:
P Fнабл F ,v1,v2
(функция Excel FРАСПОБР ( , 1 k 1, 2 n k )).
Можно утверждать с доверительной вероятностью γ=1–α,
что корреляционное отношение η значимо отличается от нуля,
если Fнабл Fкр ( , 1 k 1, 2 n k ) .
14.
Множественныйкорреляционный анализ
15.
Для измерения силы линейных связей одной переменной Xi ссовокупность других (k-1) переменных из их множества
(X1,…,Xn) также используются коэффициенты парной
корреляции.
Матрица коэффициентов парной корреляции R:
1
rx x
R rx x
...
r
xx
rx x
rx x
3 1
1
rx x
rx x
1
k 1
...
rx x
...
rx x
2 1
1 2
3 2
k 2
1 3
2 3
k 3
... rx x
1 r12
... rx x
r21 1
r
R
r32
... rx x
31
или
... ...
... ...
r
k1 rk 2
... 1
1 k
2 k
3 k
r13
r22
1
...
rk 3
... r1k
... r2 k
... r3k
... ... , где
... 1
rij – выборочный парный коэффициент корреляции,
характеризующий тесноту линейной связи между показателями
Xi и Xj.
16.
Многомерный корреляционный анализ решаетдве задачи:
1. Определение тесноты связи одной переменной с
совокупностью остальных (k – 1) величин,
включенных в анализ;
2. Определение
тесноты
связи
между
переменными при фиксировании (исключении)
влияния остальных.
Эти задачи решаются с помощью коэффициентов
множественной
и
частной
корреляции,
соответственно.
17.
Выборочный коэффициент множественнойкорреляции и проверка его значимости
Выборочный
коэффициент
множественной
корреляции
R j ,1, 2, j 1, j 1,... k
R
1
R jj , где
R – определитель корреляционной матрицы R;
R jj – алгебраическое дополнение элемента rjj матрицы R.
R
2
j ,1, 2, j 1, j 1,..., k
называют
выборочным
множественным коэффициентом детерминации,
который показывает, какую долю вариации исследуемой
j-ой величины объясняет вариация остальных (k–1)
величин.
18.
Значимость множественного коэффициента корреляциипроверяется по F – критерию Фишера.
H 0 : R 2 0 , т.е. в генеральной совокупности отсутствует
корреляция.
H1 : R 2 0 .
Для проверки гипотезы вычисляется статистика:
R 2 (n k )
R 2 (k 1)
Fнабл
Fнабл
2
или
(1 R 2 ) (k 1) .
(1 R ) (n k )
Для критической области ( Fкр, ; ) критические значения
статистики находят из условия:
P( Fнабл Fкр ( , 1 k 1, 2 n k ))
(функция Excel FРАСПОБР ( , 1 k 1, 2 n k )).
Множественный
коэффициент
корреляции
значимым, если выполняется неравенство: Fнабл Fкр .
считается
19.
Частный коэффициент корреляции и проверка его значимостиВыборочный частный коэффициент корреляции Xj и Xi, при
фиксированных значениях остальных переменных (k–2)
определяется по формуле:
r ji 1, 2, ,k
R ji
R jj Rii
, где
R ji , R jj , Rii – алгебраические дополнения к соответствующим
элементам корреляционной матрицы R.
R ji ( 1) j i M ji , где M ji – минор элемента rji (определитель
матрицы, получаемой путем вычеркивания j-й строки и i-го
столбца из матрицы R).
Частный коэффициент корреляции, так же как и парный
коэффициент корреляции изменяется от –1 до +1.
20.
Для вычисления коэффициентов частной корреляции можноиспользовать рекуррентную формулу:
.
В частности, для случая трех переменных, выборочный
частный коэффициент корреляции между переменными X и Y
при фиксированных значениях переменной Z равен:
rxy z
rxy rxz ryz
(1 rxz2 )(1 ryz2 )
21.
Оценка значимости коэффициента частнойкорреляции осуществляется с помощью t-критерия
Стьюдента:
r
n l 2
tнабл
(n l 2) r
2
Sr
1 r
1 r 2 , где
r2
r – соответственно оценка частного коэффициент
корреляции;
l – число фиксируемых факторов.
H0 : R2 0
– в генеральной совокупности
отсутствует корреляция.
H1 : R 2 0 .
22.
Строится критическая область, границы которойнаходят из условия:
P t набл t
P t набл t
.
,n 2
,n 2
2
2
2
tнабл сравнивается с критическим t кр ; для
двусторонней критической области (функция Excel
СТЮДРАСПОБР (α; n l 2 )).
Если tнабл tкр , v , то коэффициент корреляции
признается значимым (т.е. Н0 отвергается).
Вывод: с вероятностью 1 можно утверждать,
что между исследуемыми переменными есть линейная
статистическая зависимость.





















 mathematics
mathematics








