Математические модели. Концепция экономико-математического моделирования

1. Математические модели

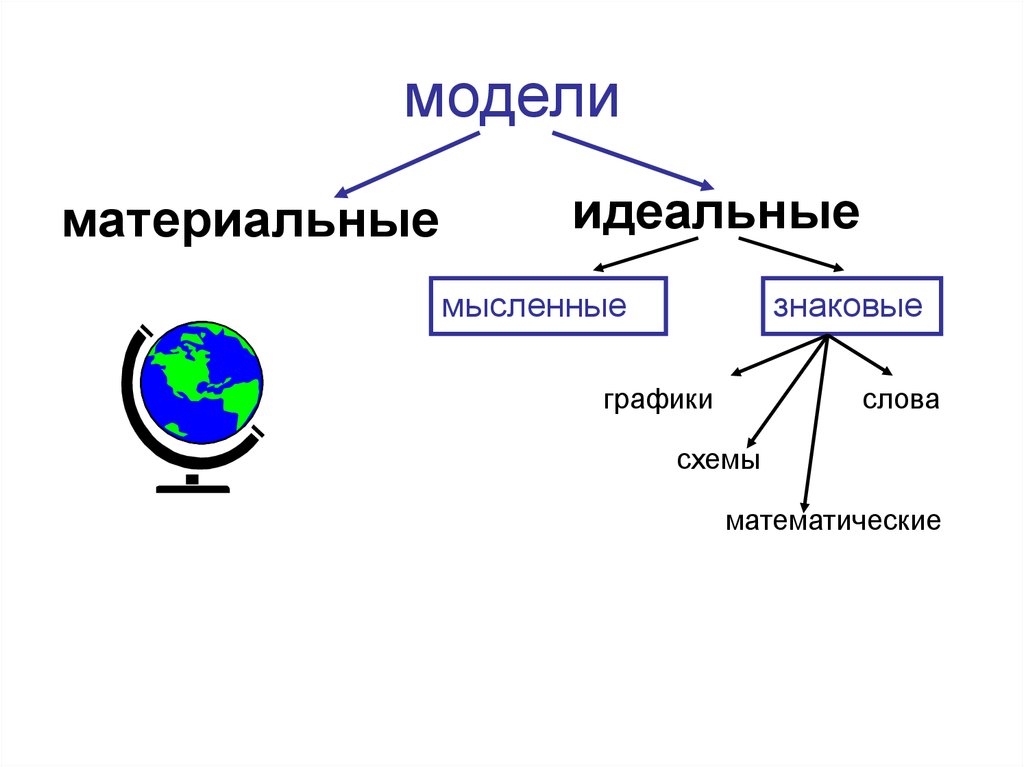
2. модели

материальные
идеальные
мысленные
знаковые
графики
слова
схемы
математические

3. модели

Познавательные
отражают существующие реальные
объекты
модель
объект
Прагматические
Нормативные
Идеал несуществующего объекта
модель
объект

4. модели

Статические
(состояние системы)
Динамические
(изменение системы
во времени)

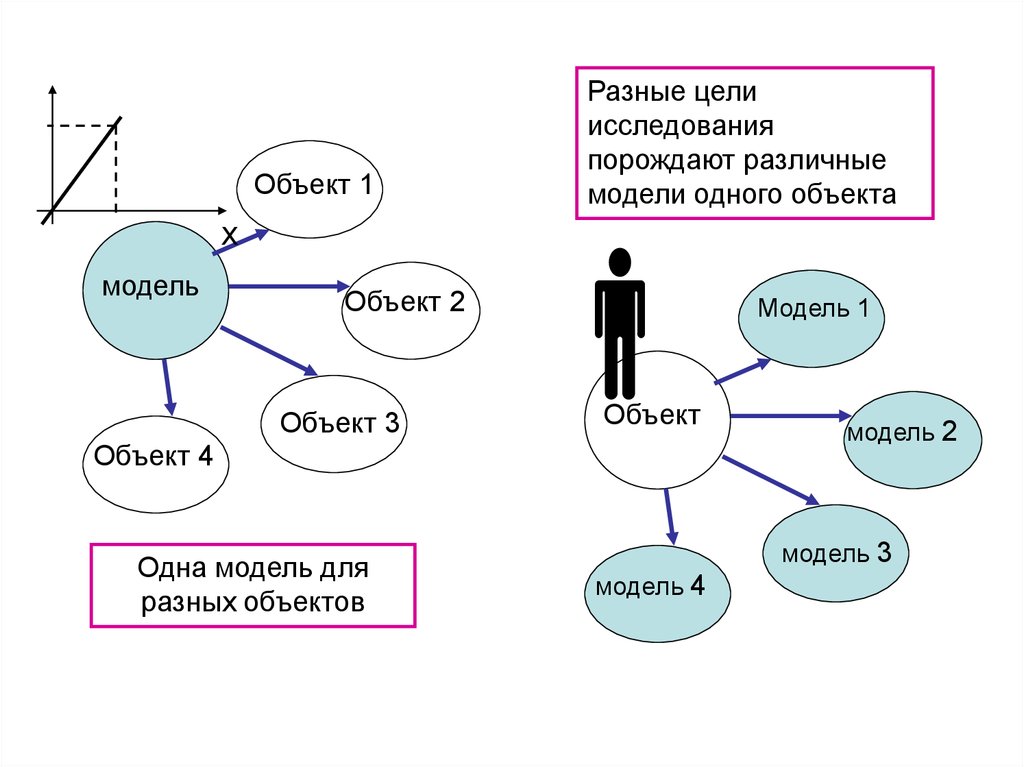
5.

Объект 1
Разные цели
исследования
порождают различные
модели одного объекта
х
модель
Объект 2
Объект 3
Модель 1
Объект
Объект 4
Одна модель для
разных объектов
модель 2
модель 3
модель 4

6.

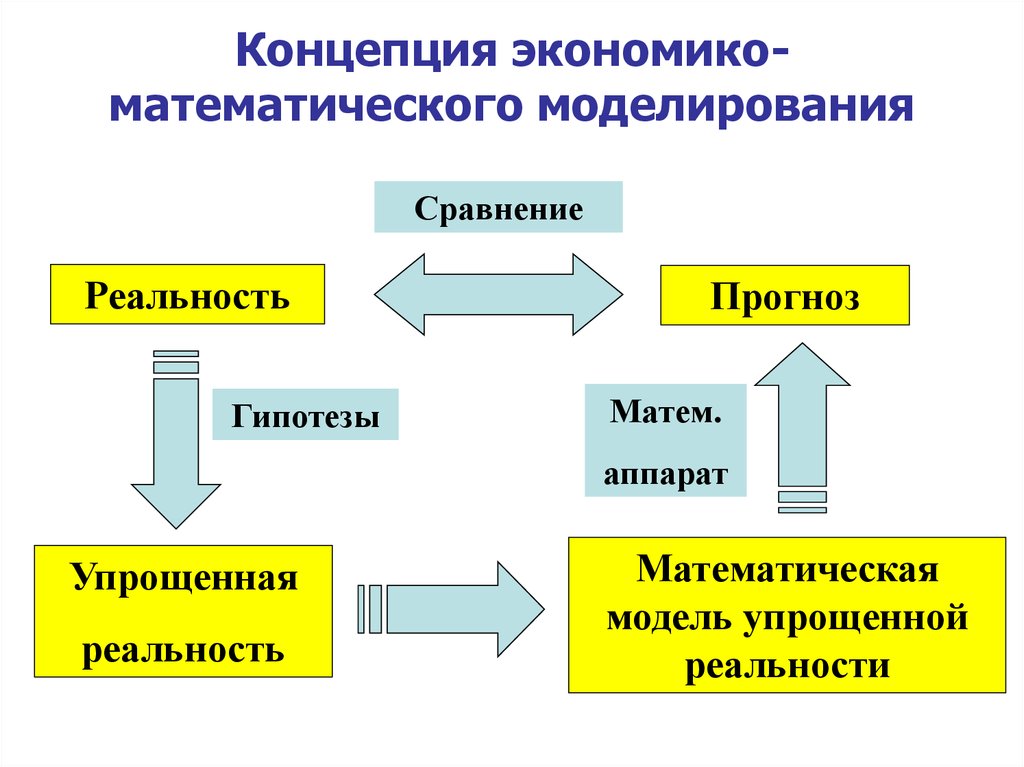
Концепция экономикоматематического моделирования
Сравнение
Реальность
Гипотезы
Прогноз
Матем.
аппарат
Упрощенная
реальность
Математическая
модель упрощенной
реальности

7.

Алгоритм экономикоматематического моделирования
Шаг 1
Выделить переменные, поведение которых в рамках поставленной
подлежит исследованию
задачи
Переменные, поведение которых подлежит
исследованию, называются эндогенными.

8.

Леонтьев В.В.
1906-1999
"Основными переменными, с помощью которых описывается экономическая система, являются объемы различных товаров и услуг,
которые производятся и потребляются, … а также цены, по которым
продаются и покупаются товары и
услуги“[*, с. 48].
* Леонтьев В.В. Применение математики в экономике // В
кн. «Экономические эссе». – М., 1990.

9.

Алгоритм экономикоматематического моделирования
Шаг 2
Выделить переменные, изменение которых
влечет изменение эндогенных переменных
Переменные, изменение которых влечет изменение эндогенных переменных, называются экзогенными.

10.

Проблема идентификации экзогенных
переменных
Переменные, находящиеся
фирмы:
P – цена товара;
под
контролем
Cv – средние переменные издержки (подразумевается, что увеличение их связано с улучшением качества продукции, снижением времени
поставки, улучшением сервиса);
M – затраты на маркетинг;
….

11.

Проблема идентификации экзогенных
переменных
Переменные, находящиеся вне контроля фирмы:
доходы и, отчасти, предпочтения целевых потребительских групп;
цены конкурентов;
затраты на маркетинг конкурентов;
….

12.

Алгоритм экономикоматематического моделирования
Шаг 3
Выдвинуть гипотезы,
экономическую реальность
упрощающие
Поскольку выделить все переменные, от которых зависит
изменение эндогенных переменных, обычно невозможно,
попытки непосредственно построить модель экономической реальности обречены на неудачу. В связи с этим
принимаются ряд тех или иных предложений (гипотез) об
экономической реальности, после чего строится математическая модель уже не исходной, а упрощенной экономической реальности.

13.

Алгоритм экономикоматематического моделирования
Шаг 4
Построить математическую модель
упрощенной экономической реальности

14.

Дедуктивный подход к экономикоматематическому моделированию
В рамках этого подхода математическая модель строится, как правило, только на основании гипотез об экзогенных переменных и механизме их воздействия на эндогенные. Затем, с
помощью построенной теоретической моде-ли,
пытаются объяснить имеющиеся частные
статистические данные (Дедукция – метод рассуждений от общего к частному).

15.

Индуктивный подход к экономикоматематическому моделированию
В рамках этого подхода, выделив переменные,
собирают исходные статистические данные для
построения модели: фиксируют значения экзогенных переменных и соответствующие им
значения эндогенных. После этого выбирается
такая форма связи переменных, которая наилучшим образом объясняет собранные данные
(Индукция – метод рассуждений от частного к
общему).

16.

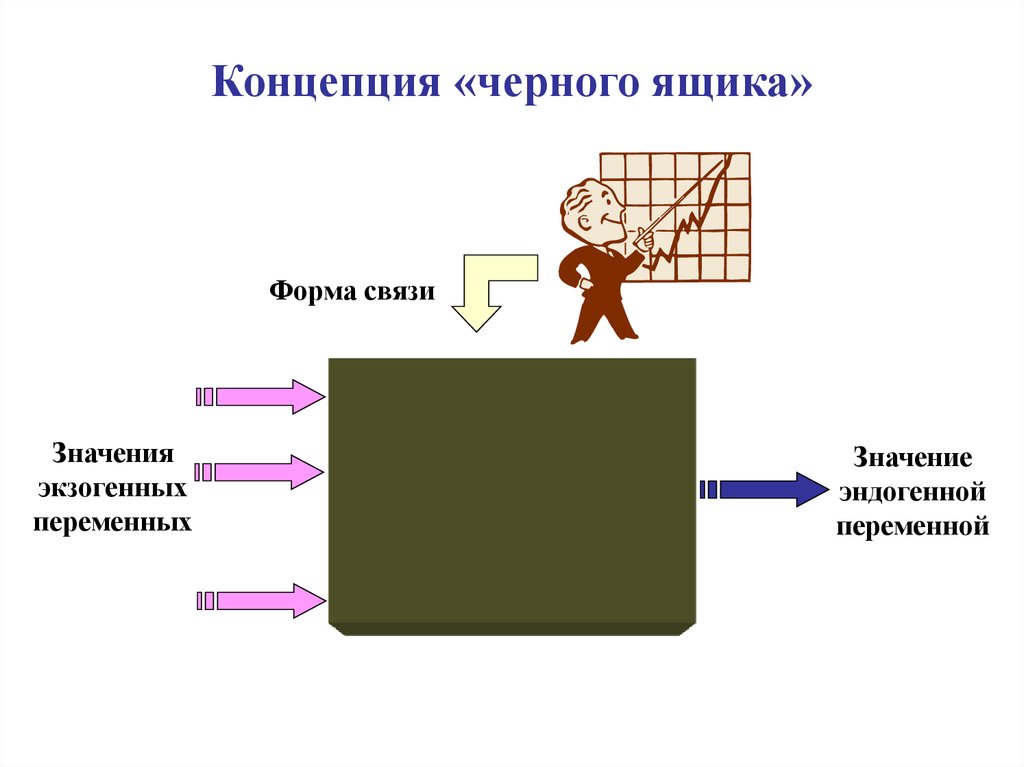
Концепция «черного ящика»
Форма связи
Значения
экзогенных
переменных
Значение
эндогенной
переменной

17.

Алгоритм экономикоматематического моделирования
Шаг 5
Использовать математическую модель
для
выдвижения
прогноза
об
экономической
реальности
(значениях
эндогенных переменных)

18.

Планирование от достигнутого

19.

Алгоритм экономикоматематического моделирования
Шаг 6
В зависимости от результатов сравнения
прогноза и реальности скорректировать
построенную модель

20.

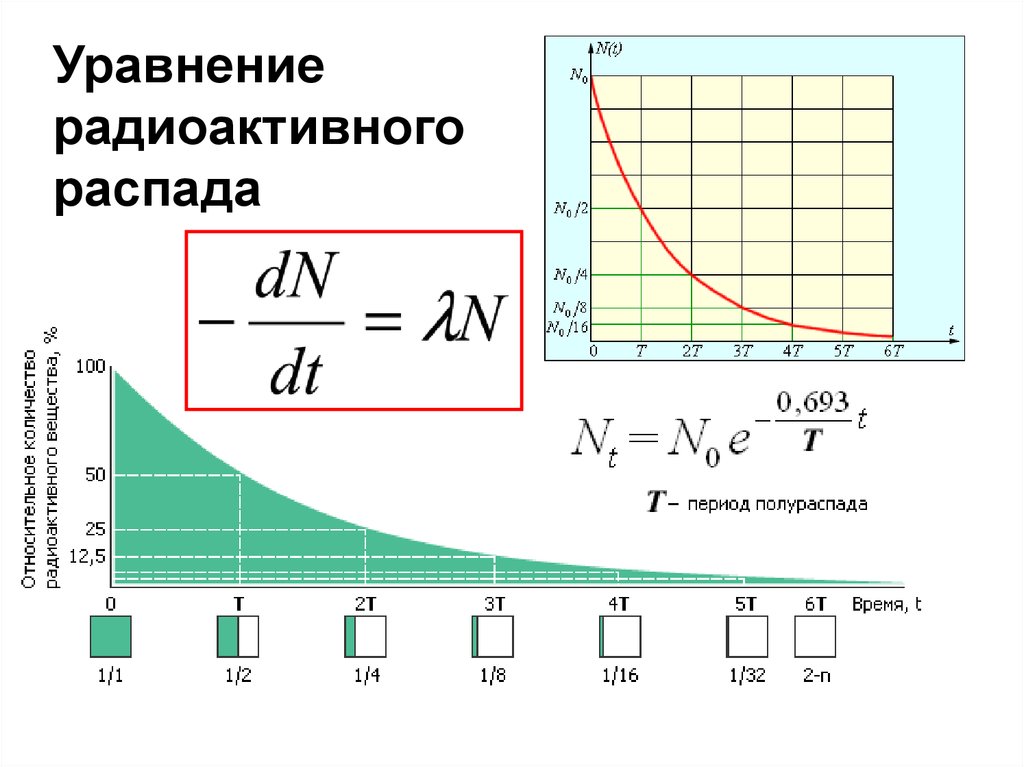
Уравнение
радиоактивного
распада

21.

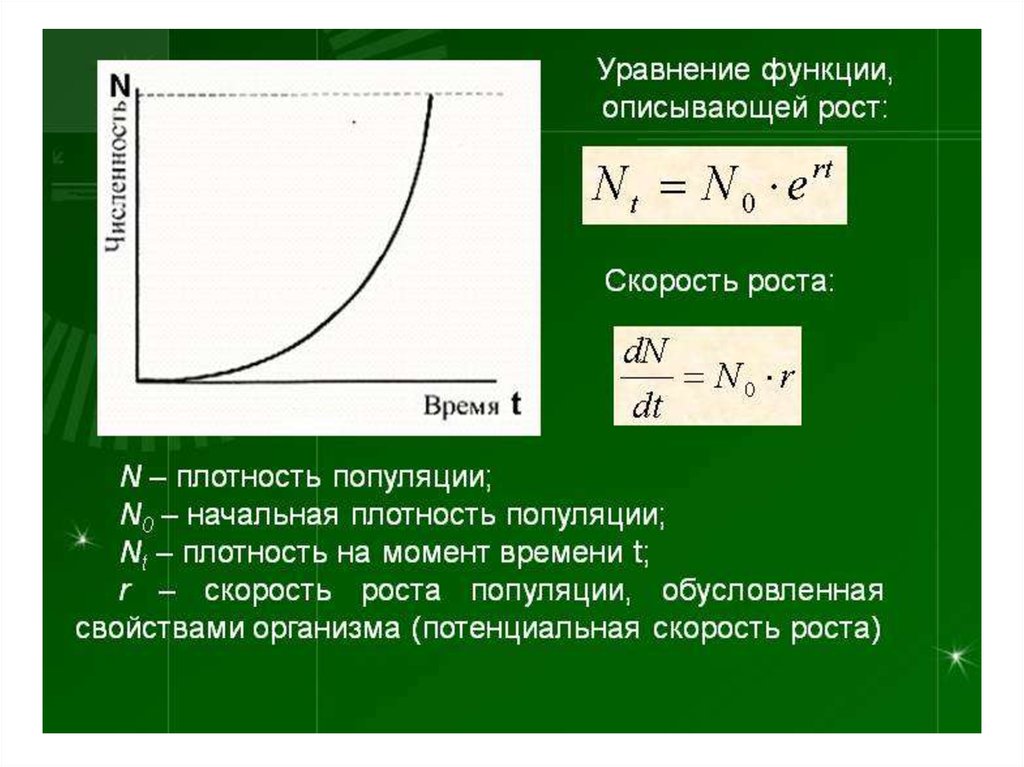
22.

23.

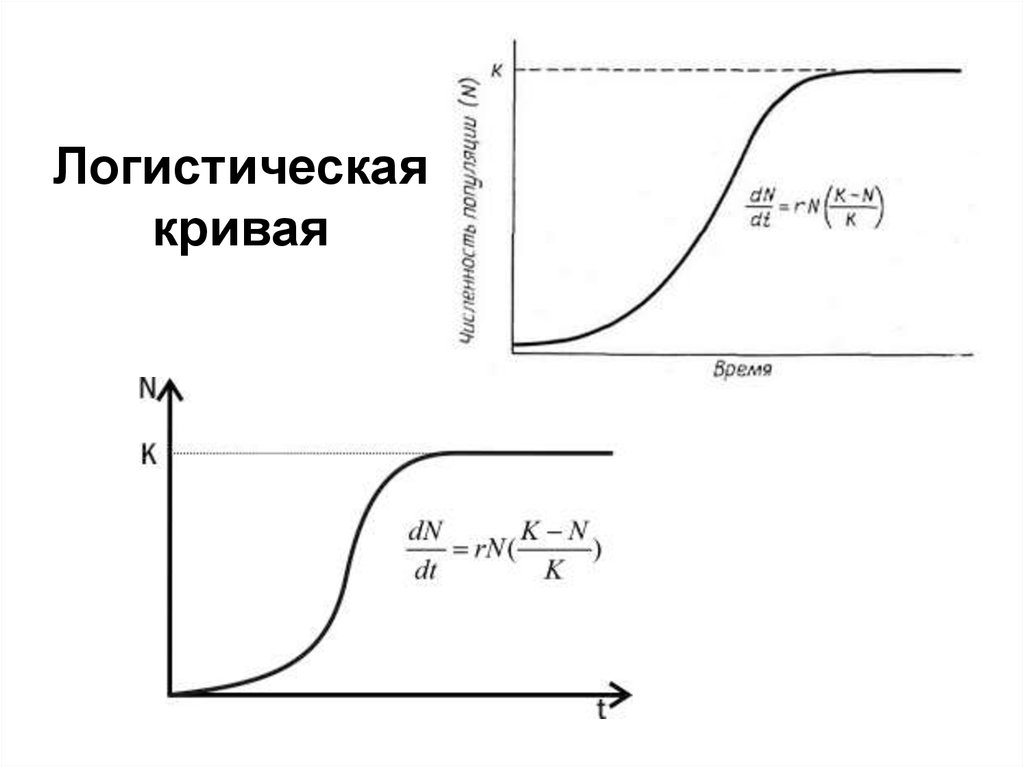
Логистическая
кривая

24. Эластичность функции

25. Абсолютные и относительные изменения

Пример: y=x2, x=10,
Пусть x = 2 – это абсолютный прирост.
Относительные приращения и их смысл:
• x/x = 0,2 – показывает, что значение
аргумента изменилось на 20% процентов;
• y/y =0,44 – показывает, что значение
функции изменилось на 44% процента;
• ( y/y)100 – показывает, на сколько процентов
изменилось значение функции.

26. Эластичность функции

y=f(x), не равной нулю и дифференцируемой в точке x 0, - число
x
Ex y
f x .
f x
f x x f x
x
f x x f x
f x
Ex y
lim
lim
.
x
0
x
0
x
f x
x
x
f x x f x
f x x f x
f x
Ex y
100
x
f x
x
Предположим, что при x/x=0,01 погрешность применения приближенной
формулы будет допустимой.
эластичность функции показывает, на сколько примерно процентов
изменится значение функции, если значение аргумента
изменится на 1%.

27. Свойства эластичности

1) Эластичность – безразмерная величина, значение которой не
зависит от того, в каких единицах измеряются переменные.
2) Если эластичности сомножителей существуют, эластичность
произведения также существует и равна сумме эластичностей
сомножителей:
Еx(f g)= Еx(f)+Еx(g)
3) Если эластичности делимого и делителя существуют,
эластичность частного также существует и равна разности
эластичностей делимого и делителя:
Еx(f/g)= Еx(f)–Еx(g)
4) Эластичности взаимно обратных функций – взаимно обратные
величины
1
Ex ( y )
E y ( x)
5) Эластичность можно представить в форме
«логарифмической производной»
d ln y
Ex ( y)
d ln x

28. Пример. Функция спроса и её эластичность

Пример. Функция спроса x 200 2 p
и её эластичность
ограничения
p 0,100 , x 0,200
прямая функция спроса
обратная функция спроса p=100 - 0.5x
x' 2
P
100
если увеличить цену на 1рубль (абсолютный прирост)
p 1
то спрос уменьшится на 2кг
R=p0x0 – доход
(выручка)
p0
x 2
Производная отражает абсолютную величину
падения спроса при повышении цены.
R
0
x0
200
X
Рис 1. Кривая спроса.
p
p
p
2
E p x
x p
x p
200 2 p
100 p

29. Ценовая эластичность спроса

• Как реагируют потребители определенного товара на изменение
его цены или цены заменяющего его товара?
• Каким образом производитель решает проблему назначения цены
на произведенный им товар?
Эластичность функции спроса
p
E p x
x p
x p
называется ценовой эластичностью спроса при цене р.
• Поскольку функция спроса является убывающей, то
Еp(x) 0.
Экономический смысл: ценовая эластичность спроса
показывает, на сколько примерно процентов
уменьшится (увеличится) объем спроса, если цена
товара увеличится (уменьшится) на 1%.
В экономической литературе эластичность берут по
модулю, т.е. со знаком плюс.
Обозначим E p x e

30. Идентификация типа спроса

Из уравнения Еp(x) = –1 найдем цену, при которой спрос нейтральный:
p
1 p 100 p 2 p 100 p 50
100 p
По цене 50 будет продано х = 200 – 2*50 = 100 кг сахара. Продавец
получит в этом случае максимальный доход (выручку) 100*50 = 5000
рублей.
В диапазоне цен от 0 до 50 спрос является неэластичным.
Например: при цене p = 20:
p
20
E p x p 20
Это означает, что если при этой цене
продавец понизит цену на 1%, то
спрос является эластичным при
ценах от 50 до 100.
p 20
100 20
1
4
СПРОС
спрос увеличится всего на
0.25%, что приведет к уменьшению
выручки, а это невыгодно продавцу.
Наоборот, продавцу выгодно при
неэластичном спросе увеличивать цену.
100 p
неэласт.
e<1
0
нейтр.
e=1
эласт.
e>1
50
Рис 2. Идентификация типа спроса.
100 P

31. Дуговая эластичность

• Оценка ценовой эластичности спроса при
неизвестной функции спроса
x p1 x p2
0,5 x p1 x p2 x1 x2 p1 p2
E p x
p1 p2
x1 x2 p1 p2
0,5 p1 p2
Пример.
x(3)=300,
x(3,15)=270,
если в качестве базовой цены взять 3, то Еp(x) –2,
а если 3,15, то Еp(x) –2,33
дуговая эластичность Еp(x) –2,16.

32. Коэффициенты эластичности выпуска по затратам ресурсов

• определяются следующими формулами:
x1
f ( x1 , x2 )
x2
f ( x1 , x2 )
e x (q)
e x (q)
2
1
f ( x1 , x2 )
x2
f ( x1 , x2 )
x1
• Коэффициенты эластичности равны отношению
предельной отдачи ресурса к средней отдаче
ресурса:
MPi
e xi (q)
APi
• Экономический смысл: коэффициент эластичности
выпуска по затратам первого ресурса показывает, на
сколько примерно процентов изменится выпуск
продукции, если затраты первого ресурса увеличить
на 1%.

33. Перекрестная ценовая эластичность

характеризует влияние цены одного товара
на спрос другого товара.
функции спроса от цен двух товаров:
x1=x1(p1, p2), x2=x2(p1, p2).
вектор цен в текущей рыночной ситуации p0=(p10, p20).
• Перекрестной ценовой эластичностью спроса на
первый товар называется число
p2
x 1 p1, p2
ep2 x 1 e12
.
x 1 p1, p2
p2
p p
0
• Аналогично вводится e21.

34. Товары замещающие и дополняющие

e12 > 0
e12 < 0
первый товар является
замещающим по отношению ко
второму (с ростом цены второго
товара спрос на него падает, а на
первый товар растет).
e12 > 0 e21 > 0
взаимозамещающие
товары
первый товар является
дополняющим по
отношению ко второму.
e12 < 0
Взаимодополняющие
товары
e12 = 0 и e21 = 0
Несвязанные
товары
e21 < 0

35. Пример

В некотором регионе недельный спрос на чай и кофе
задан формулами:
x1=40p2p1-1, x2=10p1p2-1.
• Вычислим перекрестные ценовые эластичности
спроса
e12
p 2 x1 p 2 p1 40
p x
p p
1 e 21 1 2 1 2 10 1
x1 p 2
40 p 2 p1
x 2 p1
10 p1 p 2
• независимо от цен, обе перекрестные эластичности
равны 1. Это означает, что увеличение цены одного
из товаров на 1% всегда приводит к увеличению
спроса на другой товар тоже на 1%. Товары являются
взаимозамещающими.