Понятие множества. Урок 1. 5 класс

1. Понятие множества Урок 1 5 класс

Математика
Понятие множества
Урок 1
5 класс

2.

Немного истории
Леонард Эйлер
(1707 – 1783)
Одним из первых, кто использовал для
решения задач круги, был выдающийся
немецкий математик и философ Готфрид
Вильгельм Лейбниц (1646 – 1716). В его
черновых набросках были обнаружены
рисунки с кругами. Затем этот метод
основательно развил швейцарский
математик Леонард Эйлер (1707 – 1783).
Леонард Эйлер, крупнейший математик XVIII
века, родился в Швейцарии. В 1727г. по
приглашению Петербургской академии наук
он приехал в Россию. Эйлер попал в круг
выдающихся математиков, получил большие
возможности для создания и издания своих
трудов. Он работал с увлечением и вскоре
стал, по единодушному признанию
современников, первым математиком мира.

3.

«Множество есть
многое, мыслимое
нами как единое»
основатель теории множеств
Георг Кантор

4. Понятия теории множеств

Понятие множества является одним из
наиболее общих и наиболее важных
математических понятий. Оно было введено
в математику немецким ученым Георгом
Кантором (1845-1918).Следуя Кантору,
понятие "множество" можно определить так:
Множество- совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.

5. Придумай название для предметов и животных, собранных вместе:

НАБОР
КОЛЛЕКЦИЯ МАРОК КАРАНДАШЕЙ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
СТАЯ ПТИЦ
СТАДО КОРОВ

6.

Множество – совокупность объектов,
объединенных по какому–нибудь признаку.
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество,
называются элементами множества.

7.

множество
элемент
Множество
четырехугольников
Трапеция, параллелограмм, ромб,
квадрат, прямоугольник
Пространственные тела
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
Натуральные числа
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
Квадраты чисел
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
…
Цифры десятичной
системы счисления
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные
числа
10, 12, 14, 16 … 96, 98

8. Пустое множество

Множество, которое не содержит ни
одного элемента, называется пустым
множеством и обозначается (∅).
Примеры пустых множеств:
множество млекопитающих, имеющих
шесть ног;
множество пятилетних мастеров спорта;
множество правильных треугольников, у которых
углы не равны;
множество чисел, которые больше 10, но
меньше 1.

9.

Z
Q
R
N

10.

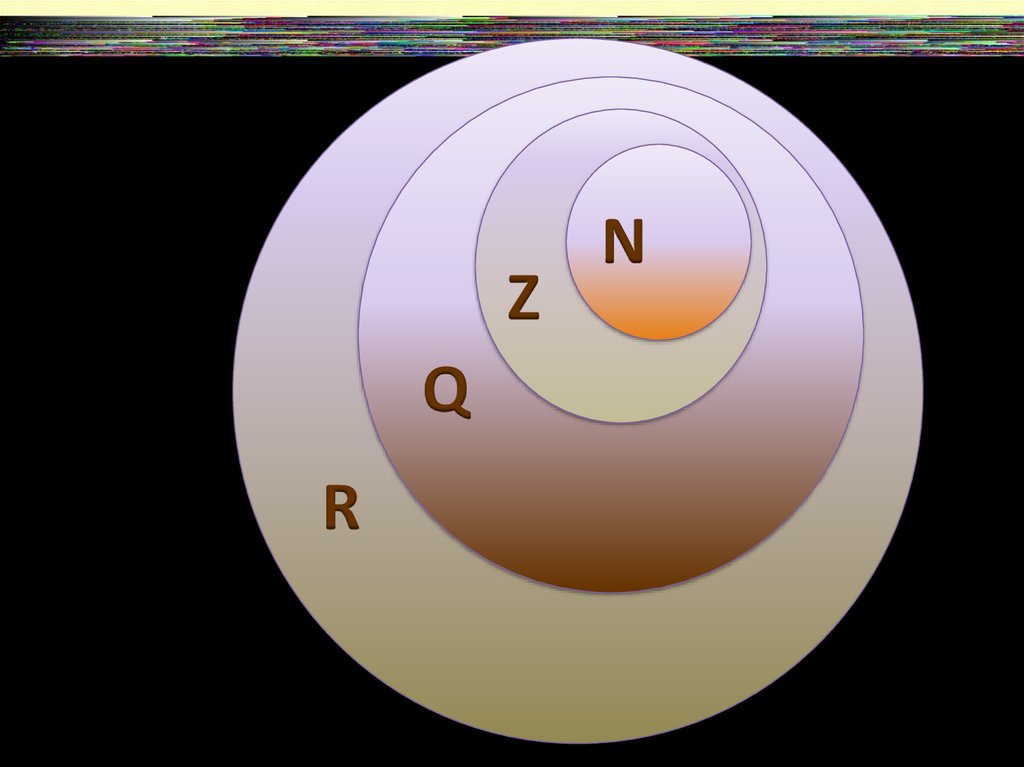
Обозначения некоторых
числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.

11. Условные обозначения

Множества:
• Заглавные буквы латинского алфавита или их
сочетание: N, Z, GR,…
• Графическое изображение – круги Эйлера ,
диаграммы Венна
Элементы множества:
• строчные буквы латинского алфавита: a, b, c,…
• натуральное изображение элемента множества:
5, лисица,
, ……
• перечисление элементов: А = {a1, a2,... , an}
∈ −значок принадлежит
∈ −значок НЕ принадлежит

12. Стандартные обозначения