Создание трёхмерной математической модели по снимкам

1.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ
Кафедра Аэрофотогеодезии
Аналитические основы создание
Тема 8_2.
трёхмерной математической модели по
снимкам
Пантюшин
Валерий Алексеевич
кандидат технических наук

2.

Учебные вопросы
1. Автоматический выбор характерных точек в стандартных
областях на снимках.
2. Автоматическая идентификация соответственных точек
(корреляция) на перекрытиях.
3. Аналитические основы трехмерного моделирования по
снимкам.
Литература
1.
2.
3.
4.
Лобанов А.Н. Аналитическая пространственная
фототриангуляция. -М.: Недра,1991.
Назаров А.С. Фотограмметрия. – М. ТетраСистемс, 2006 г
Урок фотограмметрии. 3-d моделирование.
https://vk.com/@devgam-photogrammetry
3D-моделиование с помощью программы Reality Capture
https://www.youtube.com/watch?v=9OXz6GFtABs

3.

В основе трехмерного моделирования лежат следующие
аналитические алгоритмы обработки изображений:
•автоматический выбор характерных контурных (особых) точек в
стандартных областях снимков стереопары;
•автоматическая идентификация соответственных особых точек
на стереопарах цифровых снимков (корреляция);
•взаимное ориентирование снимков исходя из условия
компланарности соответственных векторов;
•блочную или многомаршрутную фототриангуляцию (сгущение
сети особых точек), создание TIN-модели (облака точек);
•поверхностное моделирование объекта (создание ЦМР):
•текстурировние поверхностной модели (наложение текстуры на
ЦМР).

4.

1. Автоматический выбор характерных точек в стандартных областях на снимках
Под стандартными областями для выбора точек сети
фототриангуляции понимаются части снимков, расположенные на
перекрытиях в границах рабочих площадей, в местах
обеспечивающих наиболее высокую точность определения
элементов взаимного ориентирования при решении уравнений
взаимного ориентирования (например, для первой системы ЭВзО)
x1 y x2 y y 2
1 2 f 2 x1 1 x2 2 q 0,
f
f
f
Параметры стандартного расположения могут быть определены
из данного уравнения, связывающего элементы взаимного
ориентирования
(ЭВзО)
снимков
с
координатами
соответствующих
точек
стереопары
и
параллаксами,
измеренными на стандартно расположенных точках.
Исходные зависимости, определяющие значения координат
центров областей поиска образов связующих точек, могут быть
представлены в следующем виде:

5.

N центра
области
Xл
Yл,п
1
X0+b-(l/2+C)+dx/2
X0-l/2+C-dx/2
ly/2
2
X0+b-(l/2+C)+dx/2
X0-l/2+C-dx/2
a
3
X0+b-(l/2+C)+dx/2
X0-l/2+C-dx/2
-a
4
X0+l/2-C-dx/2
X0-b+(l/2-C)-dx/2
ly/2
5
X0+l/2-C-dx/2
X0-b+(l/2-C)-dx/2
a
6
X0+l/2-C-dx/2
X0-b+(l/2-C)-dx/2
-a
b= l (100%-p%);
lx
C
2
1
Xп
a
b
3
5
4
6
p
a=(ly/2-C)-dy/2;
где:
b - базис фотографирования;
а - параметр стандартного расположения
центра области;
ly lx, ly-длина стороны снимка по осям x и y;
p - величина перекрытия снимков;
dx,dy- размеры областей поиска образов
точек;

6.

7.

1. Автоматический выбор характерных точек в стандартных областях на снимках
Границы областей поиска задаются максимально возможными
линейными смещениями (dx,dy) относительно заданного центра
области поиска. Величины линейных смещений (размеры
областей поиска) зависят от размеров сторон фотоснимков (lx,ly),
координат центров областей поиска, а также от допустимой
величины (C) удаления точки от края снимка.
dx=p0-2C;
dx
;
p0=100%-k*(100%-p%);
dy
ly/2-C
po
dy =
(ly / 2 2C )
2
P0 -величина продольного перекрытия снимков,
bпр
k=
; bпр - базис проектирования;
b

8.

Последовательность автоматического выбора образов точек в
стандартных областях на цифровом снимке.
Цифровой
снимок
Область
поиска
Совокупность
образов
Информативный
образ

9.

Под образом точки цифрового снимка будем понимать двумерный
массив значений яркости ЭИ текстура и структура которых имеет
отличительные особенности.
В целях выбора на цифровом снимке совокупности образов точек,
не являющихся изображением фона, использують критерии,
базирующиеся на положении теории вероятности о максимальной
информации
при
наибольшей
неопределенности
(равновероятности) распределения элементов изображения,
составляющих образ точки. Среднее количество информации о
вероятности появления в образе точки ЭИ с разными значениями
оптической плотности может быть вычислено по формуле
n
Шеннона:
H pj log pj
j 1
nj
где pj n - вероятность появления j-того значения яркости ЭИ.
Вычисленное значение энтропии, близкое к единице, позволяет
выделить совокупность образов, не являющихся изображением
фона (рис.1 фрагменты б, в, г, д, е, ж, к).

10.

Вычисленное значение энтропии, близкое к единице,
позволяет выделить совокупность образов, не являющихся
изображением фона. В таких образах элементы
изображения, имеющие разные значения оптической
плотности, занимают примерно равные площади.

11.

Оценка текстуры (особенности пространственного размещения
элементов изображения, составляющих образ точки) выполняется
с учетом статистической зависимости смежных элементов
изображения, составляющих группу.
Величина, характеризующая текстуру образа точки, вычисляется
по формуле приближения к энтропии:
Gvj
где
mv
p( B ) * log p( B )
i
i
i 1
Gvj - v- тое приближение к энтропии j-того фрагмента
образа точки;
Bi – группа из v ЭИ, в которой каждый элемент может
принимать любую из m градаций КОП;
m- число уровней квантования оптической плотности
изображения;
mv – возможное число групп ЭИ;
p(Bi) – вероятность появления i-той группы ЭИ;

12.

Оценка
структуры
(характеристики
величины
пространственной взаимосвязи между группами ЭИ,
составляющих образ) выполняется на основе анализа
статистической избыточности R во фрагментах образа
Gv
точки:
R 1
H max
а)
б)
в)
г)
Значение показателя информативности R вычисленное по
данному критерию, позволяет выделить более "четкую" с
визуальной точки зрения структура образа, составленного
из элементов изображения (образ точки б).

13.

2. Автоматическая идентификация соответственных точек (корреляция) на перекрытиях
Идентификация точек на паре снимков рассматривается как
статистическая задача распознавания изображений при
наличии помех и искажений и решается на основе
динамической теории зрения с использованием оптикоэлектронных или программных блоков, называемых
корреляторами.
Опознавание точки левого снимка на правом сводится к
выбору некоторого образа R на левом снимке и поиску на
правом снимке такого образа Rꞌ, чтобы расстояние между
ними было минимальным: | R - Rꞌ'| = min.
(1)

14.

2. Автоматическая идентификация соответственных точек (корреляция) на перекрытиях
Практически для автоматического опознавания точки
необходимо:
1. Выбрать на левом снимке образ R в виде области
размером nхn пикселов, в центре которой размещена
опознаваемая точка, и определить его характеристикуэталон, на основе которой будет выполняться проверка
условия (1);
2. Определить на правом снимке зону поиска размером mхm
пикселов (m»n) вероятного расположения искомой точки с
координатами центра
3. Последовательным перемещением области размером nхn
в границах зоны поиска на один пиксел вначале по оси х, а
затем по оси у создать на правом снимке серию образов Rꞌ и
определить характеристики каждого из них.

15.

2. Автоматическая идентификация соответственных точек (корреляция) на перекрытиях
4.Сопоставить характеристики каждого образа Rꞌ с характеристикойэталоном вектора R. Искомая точка на правом снимке будет
расположена в центре образа R, для которого выполняется условие (1).
Установление степени соответствия векторов R и Rꞌ может быть
выполнено различными путями, из которых наиболее распространенным
является расчет коэффициентов корреляции между яркостями
элементов образа R и каждого из образов Rꞌ на правом снимке с
использованием формулы:
где ро и р'о - средние яркости элементов зон (фрагментов), соответст­
вующих образам левого R и правого Rꞌ снимков.
Коэффициенты, подсчитанные для сочетаний образа R со всеми
образами Rꞌ образуют корреляционную матрицу: максимальное
значение ее элемента соответствует наиболее тесной связи яркостей
сравниваемых участков левого и правого снимков, и, следовательно,
выполнению условия (1). Так что искомая точка лежит в центре образа
Rꞌ с максимальным коэффициентом корреляции.

16.

2. Автоматическая идентификация соответственных точек (корреляция) на перекрытиях
4.Сопоставить характеристики каждого образа Rꞌ с характеристикойэталоном вектора R. Искомая точка на правом снимке будет
расположена в центре образа R, для которого выполняется условие (1).
Установление степени соответствия векторов R и Rꞌ может быть
выполнено различными путями, из которых наиболее распространенным
является расчет коэффициентов корреляции между яркостями
элементов образа R и каждого из образов Rꞌ на правом снимке с
использованием формулы:
где ро и р'о - средние яркости элементов зон (фрагментов), соответст­
вующих образам левого R и правого Rꞌ снимков.
Коэффициенты, подсчитанные для сочетаний образа R со всеми
образами Rꞌ образуют корреляционную матрицу: максимальное
значение ее элемента соответствует наиболее тесной связи яркостей
сравниваемых участков левого и правого снимков, и, следовательно,
выполнению условия (1). Так что искомая точка лежит в центре образа
Rꞌ с максимальным коэффициентом корреляции.

17.

3. Аналитические основы создания 3-D моделей по снимкам.
В основе методов трехмерного моделирования положены аналитические
основы фототриангуляции - метода определения координат и высот точек
местности, посредством засечек по перекрывающимся снимкам. Выполняется
путем построения и уравнивания системы пространственных треугольников,
включающих одноименные проектирующие лучи и базис фотографирования.
Координаты точек получают путем построения фотограмметрических моделей
объекта (местности) по снимкам, принадлежащим одному или нескольким
перекрывающимся маршрутам.
Элементарное звено фототриангуляции - одиночная модель (связка
проектирующих лучей) образуется в результате взаимного ориентирования
стереопар фотоснимков. Соединение элементарных звеньев в единую сеть
выполняется по связующим точкам – соответственным точкам соседних
моделей. В результате соединения отдельных звеньев образуется свободная
фотограмметрическая сеть.

18.

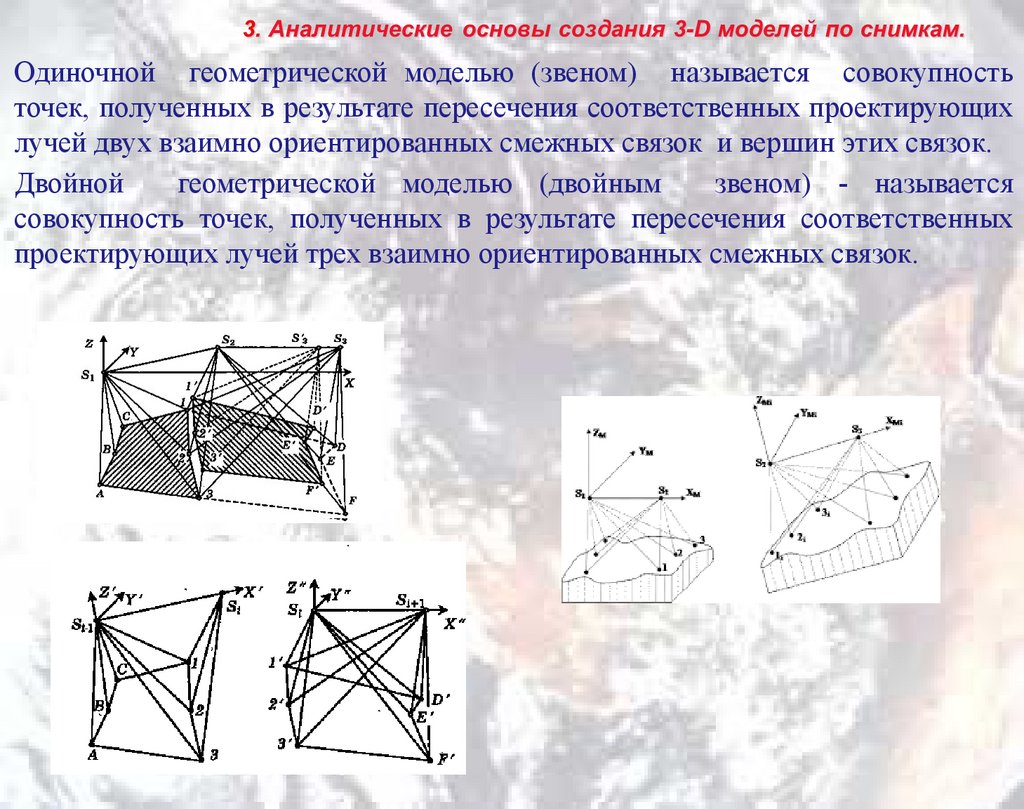
Одиночной геометрической моделью (звеном) называется совокупность
точек, полученных в результате пересечения соответственных проектирующих
лучей двух взаимно ориентированных смежных связок и вершин этих связок.
Двойной
геометрической моделью (двойным
звеном) - называется
совокупность точек, полученных в результате пересечения соответственных
проектирующих лучей трех взаимно ориентированных смежных связок.

19.

3. Аналитические основы создания 3-D моделей по снимкам.
Три смежных снимка, принадлежащие двум смежным стереопарам и имеющие
зону тройного продольного перекрытия, образуют фотограмметрический
триплет. Средний снимок Si и точки тройного продольного перекрытия входят
как в предыдущую стереопару (Si-1), так и в последующую (Si+1).
Фотограмметрический триплет строится в координатной системе SiXYZ,
начало которой совмещено с центром фотографирования среднего снимка Si,
а оси X и У параллельны осям координат его внутренней координатной
системы оху. Взаимное ориентирование снимков триплета выполняется в
линейно-угловой системе; дополнительно к условиям компланарности
соответствующих векторов в обеих стереопарах используется масштабное
условие, требующее равенства длин проектирующих лучей для связующих
точек, расположенных в зоне тройного продольного перекрытия.

20.

Вопрос 3_1. Способы маршрутной фототриангуляции.
Построение фотограмметрической модели можно выполнить в произвольной
координатной системе, выбор которой не связан ни с базисом
фотографирования, ни со снимками стереопары (рис.1), в линейно-угловой
(рис.2) системе , или в базисной (рис.3).
Рис.3
Рис. 1
Рис. 3
Рис. 2
Во всех случаях взаимное ориентирование выполняется2 строгим способом по
x1 y
x y
y
избыточному числу точек,
1 2 2 f 2 x1 1 x2 2 q 0,
f
f
f
а определение пространственных координат точек в избранной координатной
системе - с произвольно выбранным базисом В и на основе формул прямой
фотограмметрической засечки (9.3) и (9.5)
R0 ( r1 r2 ) 0.
N
BY Z 2 BZ Y2 BZ X 2 BX Z 2 BX Y2 BY X 2
(9.3)
Y1 Z 2 Y2 Z1
X 2 Z1 X 1 Z 2
X 1 Y2 X 2 Y1
N
B
B
(9.5)
0
0
p0
x1 x2
X 1
X Xs
Y Ys N Y1
Z
Z Zs
1
R2 r2 0.
R1 N r1
R2 R1 R0

21.

Вопрос 3_1. Способы маршрутной фототриангуляции.
Способ независимых моделей
Объединение одиночных модели в общую модель маршрута выполняют
последовательным соединением: вторая модель присоединяется к первой так,
чтобы соответствующие связующие точки совпали; третья модель — ко второй
и так до последней модели.
X X 0 X X 0 a1a2 a3 X X Г0
X
Y Y0 Y Y0 b1b2b3 * Y t YГ0 A Y t
Z Z Z Z c c c Z
Z
0 0 1 2 3 Z Г0
X, Y, Z— координаты точки второй модели в системе S1XXYZ первой;
Х0, Y0, Z0 — координаты центра проекции S2 в системе S1XXYZ первой;
Значения ΔХ, ΔY, ΔZ— приращения координат точки второй модели относительно
центра проекции S2
X', Y', Z'— координаты точки второй модели в системе S1XYZ
аi, bi сi, — направляющие косинусы, зависящие от углов поворота углов ζ. η и θ
второй модели относительно первой;
t —масштабный коэффициент.

22.

Вопрос 3_1.Способы маршрутной фототриангуляции
Способ независимых моделей
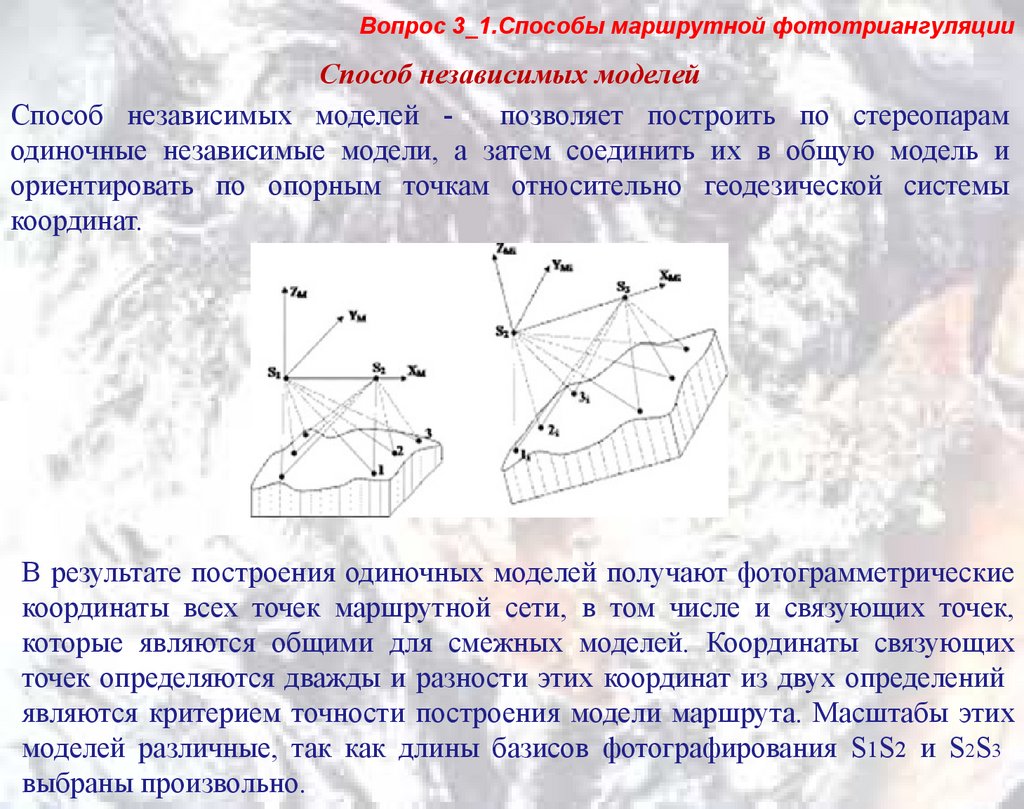
Способ независимых моделей позволяет построить по стереопарам
одиночные независимые модели, а затем соединить их в общую модель и
ориентировать по опорным точкам относительно геодезической системы
координат.
В результате построения одиночных моделей получают фотограмметрические
координаты всех точек маршрутной сети, в том числе и связующих точек,
которые являются общими для смежных моделей. Координаты связующих
точек определяются дважды и разности этих координат из двух определений
являются критерием точности построения модели маршрута. Масштабы этих
моделей различные, так как длины базисов фотографирования S1S2 и S2S3
выбраны произвольно.

23.

Вопрос 3_1. Способы маршрутной фототриангуляции.
Способ частично зависимых моделей
Основу этого способа составляет последовательное построение по стереопарам
частично зависимых моделей в единой заранее установленной
фотограмметрической системе координат и приведение их к общему масштабу.
Первую модель получают взаимным ориентированием снимков, произвольно выбирая
элементы внешнего ориентирования левого снимка (первого снимка маршрута).
Вычисляют дирекционный угол и угол наклона базиса фотографирования, а также
элементы внешнего ориентирования правого снимка. При этом длину базиса
фотографирования выбирают произвольно.
Последующие модели строят аналогично, но в качестве элементов внешнего
ориентирования левого снимка второй (последующей) стереопары принимаются не
произвольные величины, а полученные при обработке первой (предыдущей)
стереопары.

24.

Вопрос 3_1.Способы маршрутной фототриангуляции.
Способ связок
В способе связок фотограмметрическая сеть строится и уравнивается
одновременно по всем снимкам данного маршрута.
В основу рассматриваемого способа положены уравнения коллинеарности
векторов (1) , приведенные к линейному виду (2).
X*
a ( X X S ) b1 (Y YS ) c1 ( Z Z S )
x x0 f * f 1
Z
a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
Y*
a ( X X S ) b2 (Y YS ) c2 ( Z Z S )
y y0 f * f 2
Z
a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
X xвыч xизм
x*
X XS
*
T
(1), где y A Y YS
*
Z Z
z
S
x
x
x
x
x
x
x
x
x
X s
Ys
Z s
f
x0
y0 ;
X s
Ys
Z s
f
x 0
y0
y
y
y
y
y
y
y
y
y
y yвыч yизм
X s
Ys
Z s
f
x0
y0
X s
Ys
Z s
f
x 0
y0
(2)
Для каждой опорной точки составляются уравнения поправок:
X l X X
Y lY Y
Z lZ Z
где
l 0
l Y 0
l z 0
X,Y,Z – измеренные координаты
–приближенные
значения
координат

25.

Вопрос 3_2. Способы блочной фототриангуляции.
Способ связок
С геометрической точки зрения сеть фототриангуляции по методу связок
строится под условием пересечения соответственных проектирующих лучей
связок в точках объекта Уравнения поправок, соответствующие условным
уравнениям уравнения коллинеарности имеют вид:
a1 X S a2 YS a3 Z S a4 a5 a6 a7 X a8 Y a9 Z l x x
.
b1 X S b2 YS b3 Z S b4 b5 b6 b7 X b8 Y b9 Z l y y
Для каждой планово-высотной опорной точки составляются уравнения поправок: X l
X
X
Y lY Y
Z lZ Z
Если с помощью системы GPS были определены координаты центров
проекций снимков S и угловые элементы внешнего ориентирования снимков
, , , то для каждого снимка составляются уравнения поправок:
X S l Xs Xs
YS lYs Ys
Z S lZs Zs
где
l s So S
l s So S ,
l s So S
где
o
o ,
o

26.

Вопрос 3_2. Способы блочной фототриангуляции.
Полученную таким образом систему уравнений поправок решают методом
приближений по методу наименьших квадратов под условием PV=min.
В результате решения находят значения элементов ориентирования снимков
сети и координаты точек сети
S1
m1
n1
l3
m2
n2
m3
S6
S5
S4
n4
S3
S2
m4
n5
m5
k3
l6
m6
k6
L
M
K
N
Общее количество неизвестных, определяемых при построении и уравнивании
блочной сети, можно определить по формуле:
N 6n 3k ,
где
n – количество снимков в сети;
k – количество определяемых точек (включая опорные геодезические
точки).

27.

Вопрос 3_2. Способы блочной фототриангуляции.
S1
m1
n1
l3
m2
n2
m3
S6
S5
S4
n4
S3
S2
m4
n5
m5
k3
l6
m6
k6
L
M
K
N
Общее количество уравнений поправок можно определить по формуле:
M 2m 3c 2i l 3 S 3 j
в которой:
m – общее количество измеренных на снимках точек;
c - количество планово-высотных опорных точек;
i - количество плановых опорных точек;
l – количество высотных опорных точек;
S – количество центров проекций снимков, координаты которых были определены с
помощью системы GPS.
Ј – количество снимков, угловые элементы которых были определены.
Для блочной сети, изображенной на рис
N 6 8 3 20 108
n=8, а k=20, поэтому