Similar presentations:
Нерозгалужене коло з активним опором та індуктивністю
1. Лекція 4
Нерозгалужене коло з активнимопором та індуктивністю
Лекція 4
Теоретичні основи електротехніки
1
2. Електричне коло змінного струму характеризують трьома параметрами
активним опором,індуктивністю
ємністю
Таким чином, у колах змінного струму
існують наступні види навантаження:
Активне
Індуктивне
Ємнісне
Лекція 4
Теоретичні основи електротехніки
2
3. Активний опір
Розглянемо коло змінного струму з одним активним опором іуявимо, що вплив індуктивності та ємності на процеси
незначний.
У колі з резистивним елементом при синусоїдній напрузі
u U m sin t
проходе синусоїдний струм, так як по закону Ома:
i
U
u
m sin t I m sin t
R
R
Тобто, у будь-який момент часу миттєве значення струму
пропорційно миттєвому значенню напруги і графіки струму та
напруги будуть співпадати за напрямом.
У колах з активним опором струм й напруга збігаються за
фазою (синфазні):
0
u
Лекція 4
Теоретичні основи електротехніки
i
3
4. Активний опір
Спад напруги на активному опорі тежзбігається за фазою зі струмом.
Закон Ома для усіх значень струму та
напруги в цьому колі буде:
U I R,
U m I m R,
u i R
Лекція 4
Теоретичні основи електротехніки
4
5. Активний опір
Хвильова та векторна діаграми струму інапруги у колі з резистивним елементом
приведенні на рис.3
u,В
IR
i,А
UR
ωt, рад
Рисунок 3 - Хвильова та векторна діаграми струму і напруги у
колі з резистивним елементом
Лекція 4
Теоретичні основи електротехніки
5
6. Індуктивний опір
Індуктивність у колах змінного струмувраховують
реактивним
індуктивним
опором, величина якого збільшується з
ростом частоти:
x L L 2 fL,
де L - індуктивність котушки, Гн
- кутова частота, с-1
f - частота струму, Гц
Лекція 4
Теоретичні основи електротехніки
6
7. Індуктивність
u eL Ld ( I m sin t )
di
d (sin t )
L
LI m
LI m cos t x L I m cos t U m cos t
dt
dt
dt
Відомо, що синусоїда випереджує косинусоїду на 90º cos
sin( 90)
R 0
u U m cos t U m sin( t 90 ) e L u E Lm sin( t 90 ) E Lm sin( t 90 )
А зсув за фазою між напругою та струмом буде:
u i 90 0 90
R 0
Таким чином, напруга у колі з ідеальною котушкою
випереджує струм на 90º (чи струм, витках котушці, відстає
від прикладеної напруги на 90º).
Лекція 4
Теоретичні основи електротехніки
7
8. Коло з індуктивністю
i, u, eLi
u
UL
ω
eL
IL
ωt, рад
π
2π
φ
T
EL
Рисунок 5 - Хвильова та векторна діаграми струму, напруги,
ЕРС самоіндукції у колі з індуктивним елементом
Лекція 4
Теоретичні основи електротехніки
8
9. Ємнісний опір
Активнийопір
та
індуктивність
конденсаторів так малі, що ними можна
знехтувати. Ідеальний ємнісний елемент
(конденсатор)
має
ємність,
яка
характеризує
його
здатність
накопичувати
електричні
заряди
і
створювати
електричне
поле.
Позначення ємнісного опору в схемах та
його залежність від частоти струму
вказані на рис.6.
Лекція 4
Теоретичні основи електротехніки
9
10. Коло з індуктивністю
XС,Омc
i
~u
f,Гц
Рисунок 6 - Позначення ємнісного опору в
схемах (1) та його залежність від частоти
струму (2)
Лекція 4
Теоретичні основи електротехніки
10
11. Коло з ємнісним опором
Конденсатор характеризується реактивнимємнісним опором:
1
1
xC
,
c 2 fc
Лекція 4
Теоретичні основи електротехніки
11
12. Коло з ємнісним опором
Відомо, що синусоїда випереджуєкосинусоїду на 90º: i I m sin( t 90)
Тоді зсув за фазою між напругою та
u i 90
струмом буде:
Таким чином, напруга у колі з ємністю
відстає від струму на 90º (чи струм
випереджує напругу 90º). Побудуємо
діаграми струму і напруги для кола з
чисто ємнісним елементом - рис.7.
Лекція 4
Теоретичні основи електротехніки
12
13. Коло з ємнісним опором
i, uu
і
IC
φ
ωt, рад
π
2π
ω
UС
T
Рисунок 7 - Хвильова та векторна
діаграми струму, напруги у колі з
ємнісним елементом
Лекція 4
Теоретичні основи електротехніки
13
14. Нерозгалужене коло з активним опором та індуктивністю
Рядкотушок
спричиняють
активний
опір
проходженню струму (тобто мають втрати енергії) і
разом з тим струм породжує в них магнітне поле.
Прикладом,
такого
пристрою
є
котушка
з
ізольованого дроту. Кожний її виток володіє
активним опором і разом з тим зчеплений з
магнітним полем. Таким чином, реальна котушка
електротехнічного пристрою має два параметра:
активний опір та індуктивність. Тому у схемі
заміщення реальну котушку можна представити
активним і реактивним індуктивним елементами,
з’єднаними послідовно.
Лекція 4
Теоретичні основи електротехніки
14
15. Нерозгалужене коло з активним опором та індуктивністю
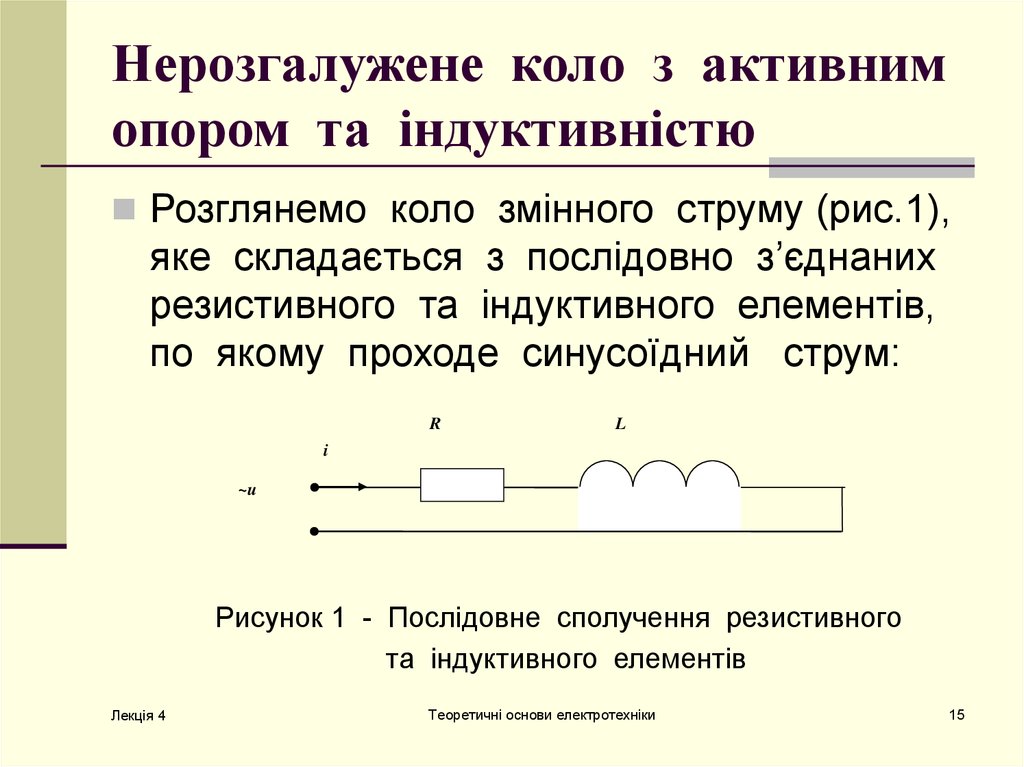
Розглянемо коло змінного струму (рис.1),яке складається з послідовно з’єднаних
резистивного та індуктивного елементів,
по якому проходе синусоїдний струм:
R
L
i
~u
Рисунок 1 - Послідовне сполучення резистивного
та індуктивного елементів
Лекція 4
Теоретичні основи електротехніки
15
16. Нерозгалужене коло з активним опором та індуктивністю
Діючий струм однаковий на усіх елементах,так як вони з’єднанні послідовно. Вияснимо,
якою буде напруга прикладена до кола, яка
витрачається у двох опорах:
спад напруги на активному опорі збігається
за фазою зі струмом і його миттєве
значення буде: u A I m R sin t U mA sin t
діюче: U A IR
Спад напруги на активному опорі називають
активною напругою
Лекція 4
Теоретичні основи електротехніки
16
17. Спад напруги на індуктивному опорі випереджає за фазою струм на кут 90º і його миттєве значення:
u L I m L sin( t 90 ) U mL sin( t 90 )діюче: U L I L Ix L
•Спад напруги на реактивному опорі називають
реактивною напругою.
• За ІІ законом Кірхгофа миттєве значення повної
напруги (на зажимах кола) у будь-який час дорівнює
геометричній сумі падінь напруги на окремих
елементах:
u
u
u
I
R
sin
t
I
L
sin(
t
90
)
A
L
m
m
Лекція 4
Теоретичні основи електротехніки
17
18. Рисунок 2 - Векторна діаграма (1), трикутники напруг (2), опорів (3) та потужностей (4) у колі з послідовним сполученням резистивного та індуктивн
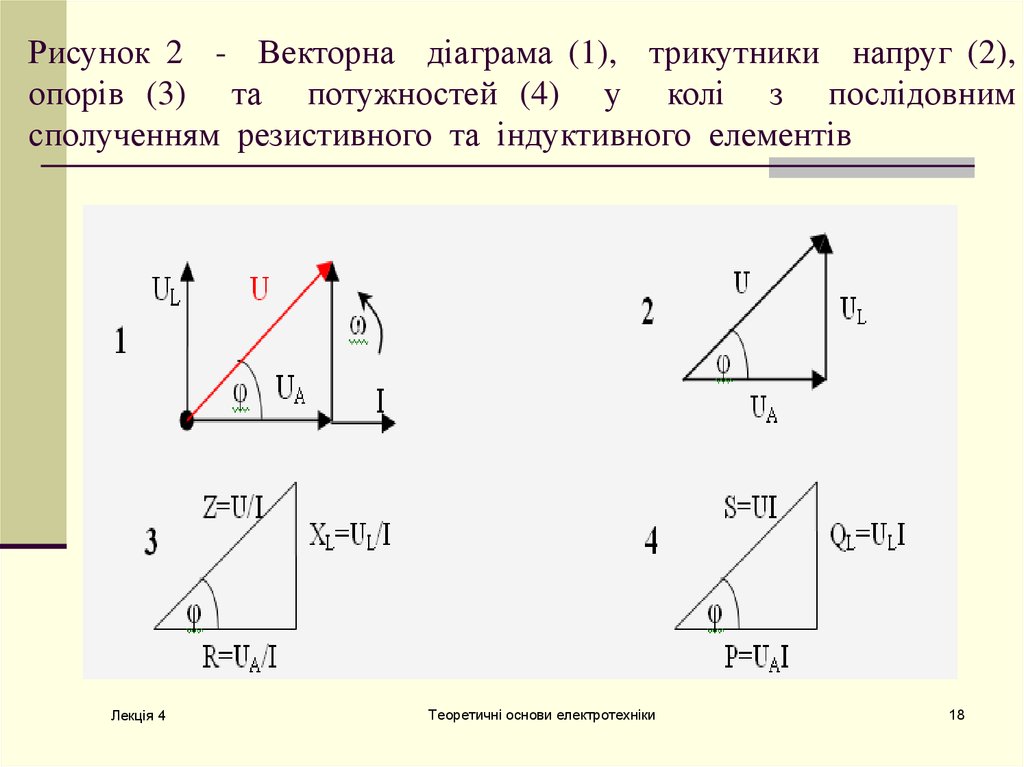
Рисунок 2 - Векторна діаграма (1), трикутники напруг (2),опорів (3) та потужностей (4) у колі з послідовним
сполученням резистивного та індуктивного елементів
Лекція 4
Теоретичні основи електротехніки
18
19. Підсумок
Розглянуто основні параметриланцюгів з активним опором та
індуктивністю.
Розглянуто векторні діаграми.
ДЗ – СР№13
Лекція 4
Теоретичні основи електротехніки
19

















 physics
physics








