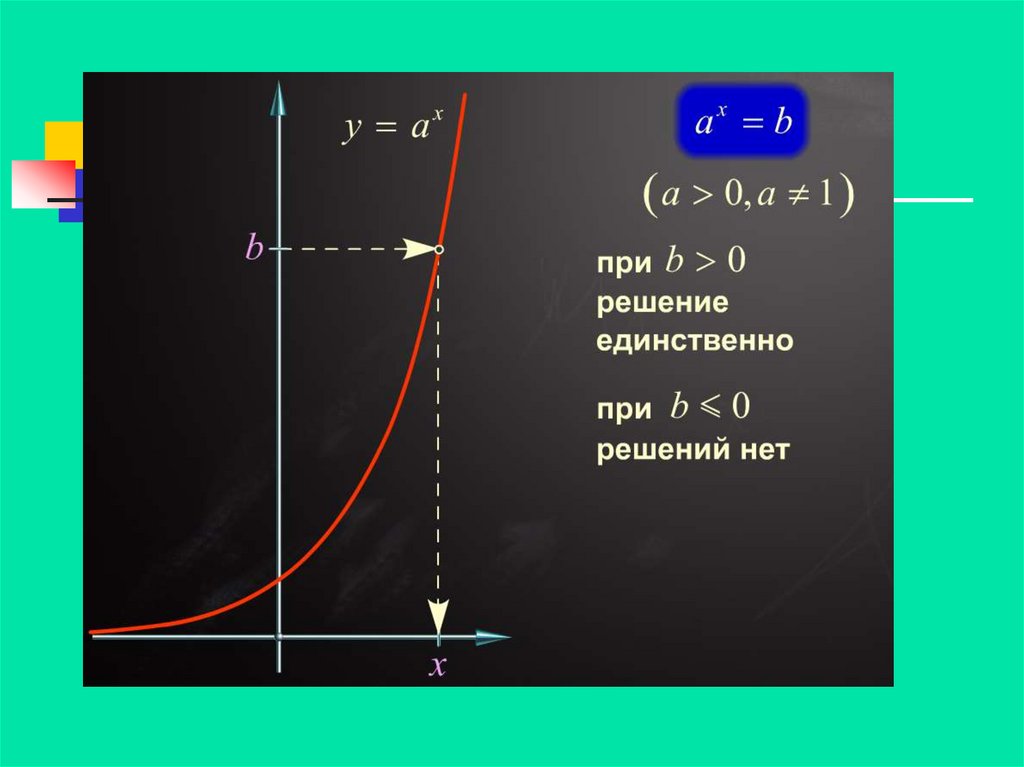
Показательные уравнения

1. Показательные уравнения

2. Показательная функция. Способы решений показательных уравнений

3.

Показательной функцией является функция
вида:
y a
x
где а>0, а≠1
y – функция
a – основание
x – показатель

4.

Исследование функции
1. Д ( f ) – любое
2. Е ( f ) – ( 0 ; + ∞ )
3. нет
4. не обладает
четностью и
нечетностью
5. монотонная
6. ↑ при а > 1
↓ при а < 1
y ax
7. ограничена снизу
8. периодична
9. обратима
10. непрерывна
11. график функции
проходит через
точку ( 0 ; 1 )
Обратим внимание на 1 и 2 пункт

5.

6.

1. Основной
Все остальные способы решения сводятся к этому
способу. Это способ приведения обеих частей
уравнения к одному основанию.
х
4 ∙ 2 = 1 │: 4
х 1
2 =4
х
–2
2 =2
х=-2
Ответ: х = - 2

7. Реши сам:

8.

9. Использование основного лог. тождества

2 7
3x
2 2
3x
ОДЗ: х – л. ч
log 2 7
52 x 1 9
5
2 x 1
ОДЗ: х – л.ч.
5
log 5 9
3 x log 2 7
2 x 1 log 5 9
1
x log 2 7
3
2 x log 5 9 1
log 5 9 1
x
2

10.

Применение формул ах ∙ bх = ( аb )х
3х
х
2 ∙ 3 = 576
х х
8 ∙ 3 = 576
х
24 = 576
х
2
24 = 24
х=2
Ответ: х = 2

11.

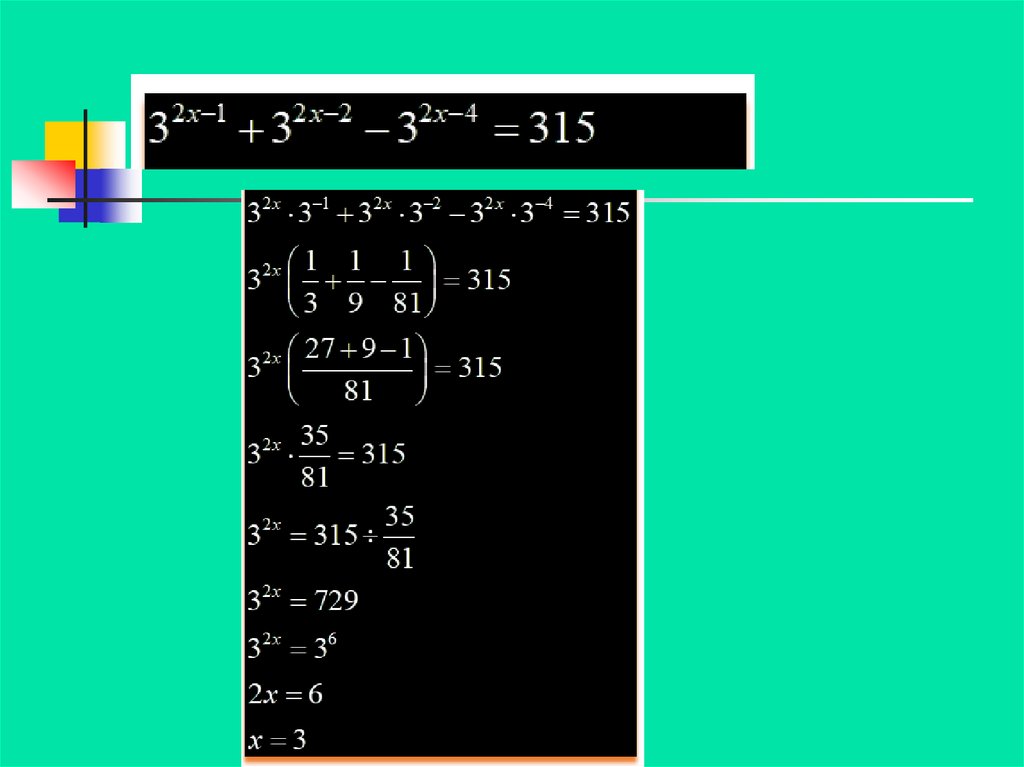
2. Вынесение общего множителя за
скобки
3
х 1
2 3
х 2
25
3x
32

12. Реши сам

ОДЗ: х – л.ч.
Ответ х=1

13.

3. Деление обоих частей уравнения на одну
из показательных функций
а) 3х = 7х │: 7х
3
=
1
7
х
х
(
3
7
)х = (
3
7
)0
х=0
Ответ: х = 0
б) 3х = 7х │: 3х
7
=
1
3
х
х
(
7
3
)х = (
7
3
)0
х=0
Ответ: х = 0

14.

4. Способ группировки
3 2
х 1
2 5
х 2
5 2
2
2 5
х
6 2 5
4
25
х
х
х
х
х 2

15.

16.

17.

5 Введение новой переменной
3
х 2
4 3 45 0
х

18.

19. Реши сам

20.

6. Логарифмирование
х
5 =3
х
log5 5 = log5 3
x∙log55= log5 3
х = log5 3
Ответ: х = log5 3

21.

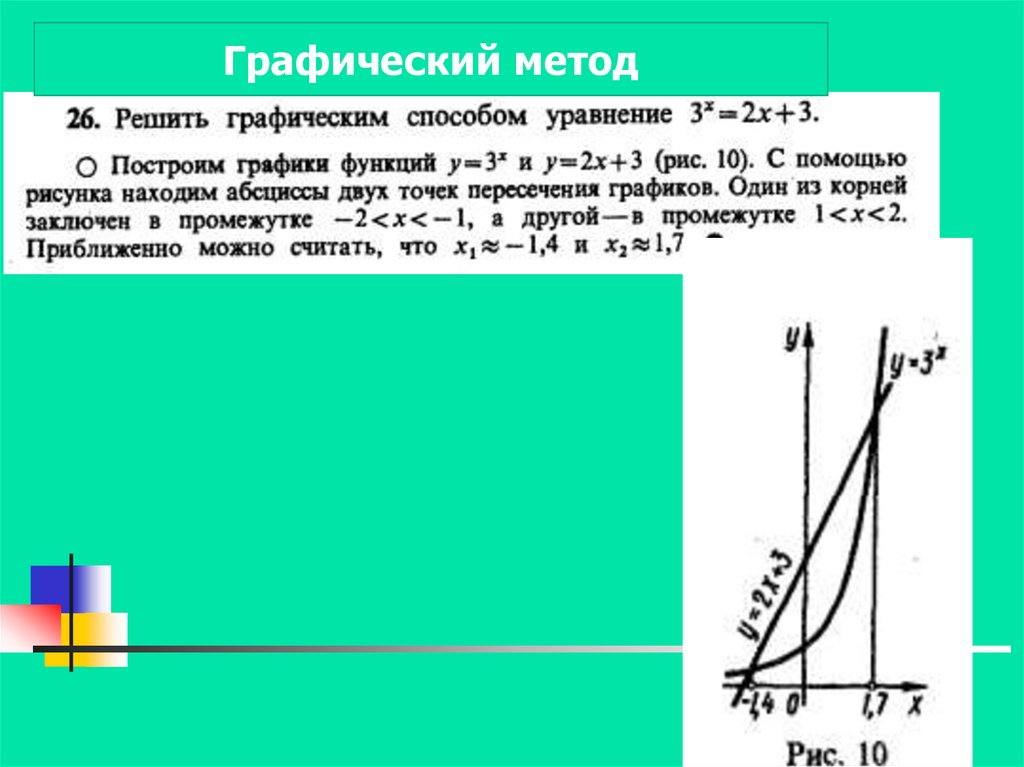
Графический метод

22. упражнения

23.

Домашнее задание(примеры
взять с преведущего слайда)
самопроверка на следующем
уроке ,мне отчет не
отправляем.
27(3,4)
28(2)
29(1,2)(4*)
30(1)(2*)
31 (1)