Similar presentations:
Геометрия. Задание №12
1. Задание №12
2. 1) Площадь четырёхугольника можно вычислить по формуле S=d1d2sinα / 2, где d1 и d2 — длины диагоналей четырёхугольника, α —
угол междудиагоналями. Пользуясь этой формулой, найдите длину
диагонали d1, если d2=7, sinα=2/7, a S=4.
3.
Решение:S = d1d2sinα / 2
2S = d1d2sinα
d1 = 2S / d2sinα
d1 = 2*4 / 7∙2 / 7
d1 = 2*4 / 2
d1 = 4
Ответ: 4.
4. 2) Площадь четырёхугольника можно вычислить по формуле S=d1d2sinα / 2, где d1 и d2 — длины диагоналей четырёхугольника, α —
угол между диагоналями.Пользуясь этой формулой, найдите длину диагонали d1,
если d2=12, sinα=5/12, a S=22,5.
5.
Решение:S=d1d2sinα / 2
2S=d1d2sinα
d1 = 2S / d2sinα
d1 = 2∙22.5 / 12∙5 / 12
d1 = 2∙22.5 / 5
d1 = 9
Ответ: 9
6. 3) Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F) пользуются формулой F= 1,8C плюс 32,
3) Чтобы перевести значение температуры по шкалеЦельсия (t °C) в шкалу Фаренгейта (t °F) пользуются
формулой F= 1,8C плюс 32, где С — градусы Цельсия,
F — градусы Фаренгейта. Какая температура (в градусах)
по шкале Фаренгейта соответствует 20° по шкале
Цельсия?
7.
Решение:F = 1.8*20+32 = 68
Ответ: 68
8. 4) Площадь четырёхугольника можно вычислить по формуле S=d1d2sinα / 2, где d1 и d2 — длины диагоналей четырёхугольника, α —
угол междудиагоналями. Пользуясь этой формулой, найдите
длину диагонали d2, если d1=17, sinα=1/3, a S=51.
9. Рішення: S = d1d2sinα / 2 2S = d1d2sinα d2 = 2S / d1sinα d2 = 2∙51 / 17∙1/3 d2 = 2∙51∙3 / 17 d2 = 18 Ответ: 18
10. 5) Центростремительное ускорение при движении по окружности (в м/с 2 ) можно вычислить по формуле a=ω2R, где ω — угловая
скорость (в с −1 ), а R —радиус окружности. Пользуясь этой формулой, найдите
радиус R (в метрах), если угловая скорость равна 8,5 с
−1, а центростремительное ускорение равно 289 м/с2.
11.
Решение:a=ω2R
R = a / ω2 = 289 / 8,5 2 = 289 / 72,25 = 4
Ответ: 4
12.
6) Площадь четырёхугольника можно вычислить поформуле S=d1d2sinα / 2, где d1 и d2 — длины
диагоналей четырёхугольника, α — угол между
диагоналями. Пользуясь этой формулой, найдите длину
диагонали d1, если d2=16, sinα=5/8, a S=45.
13.
Решение:S=d1d2sinα / 2
2S=d1d2sinα
d1 = 2S / d2sinα
d1 = 2∙45 / 16∙5 / 8
d1 = 2∙45 / 10
d1 = 9
Ответ: 9
14.
7) Центростремительное ускорение при движении поокружности (в м/с 2 ) можно вычислить по формуле
a=ω2R, где ω — угловая скорость (в с −1 ), а R — радиус
окружности. Пользуясь этой формулой, найдите радиус R
(в метрах), если угловая скорость равна 4 с −1, а
центростремительное ускорение равно 64 м/с2.
15.
Решение:a=ω2R
R = a / ω2 = 64 / 4 2 = 64 / 16 = 4
Ответ: 4
16.
8) Закон Кулона можно записать в виде F=k⋅q1q2/r2, где F— сила взаимодействия зарядов (в ньютонах), q1 и q2 —
величины зарядов (в кулонах), k — коэффициент
пропорциональности (в Н ⋅ м 2 /Кл 2 ), а r — расстояние
между зарядами (в метрах). Пользуясь формулой, найдите
величину заряда q1 (в кулонах), если k=9⋅109 Н ⋅ м 2 /Кл 2,
q2=0,004 Кл, r=500 м, а F=1,008 Н.
17.
Решение:F = k⋅q1q2 / r2
q1 = Fr2 = k⋅q2
1,008 * 500^2 / 9 * 109 * 0.004 = 0.007
Ответ: 0.007
18.
9) Площадь четырёхугольника можно вычислить поформуле S=d1d2sinα / 2, где d1 и d2 — длины диагоналей
четырёхугольника, α — угол между диагоналями.
Пользуясь этой формулой, найдите длину диагонали d2,
если d1=6, sinα=3/7, a S=18.
19.
Решение:S=d1d2sinα / 2
2S=d1d2sinα
d2 = 2S / d1sinα
d2 = 2∙18 / 6∙3/7
d2 = 2∙18∙7 / 18
d2 = 14
Ответ: 14
20.
10) Площадь четырёхугольника можно вычислить поформуле S=d1d2sinα / 2, где d1 и d2 — длины
диагоналей четырёхугольника, α — угол между
диагоналями. Пользуясь этой формулой, найдите длину
диагонали d2, если d1=10, sinα=1/11, a S=5.
21.
Решение:S=d1d2sinα / 2
2S=d1d2sinα
d2 = 2S / d1sinα
d2 = 2∙5 / 10∙1/11
d2 = 2∙5∙11 / 10
d2 = 11
Ответ: 11














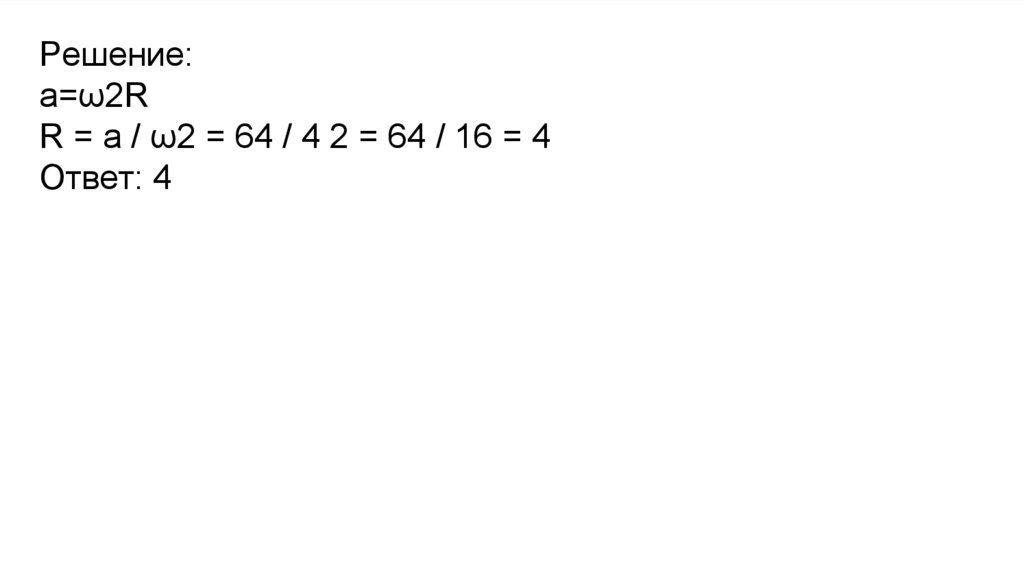






 mathematics
mathematics








