Параллельные и перпендикулярные прямые. Расстояние

1. параллельные и перпендикулярные прямые. Расстояние.

ПАРАЛЛЕЛЬНЫЕ И
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ.
РАССТОЯНИЕ.
Проект Филиной Полины 6А класс

2. Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно

ПРЯМА́Я — ОДНО ИЗ ФУНДАМЕНТАЛЬНЫХ
ПОНЯТИЙ ЕВКЛИДОВОЙ ГЕОМЕТРИИ. ПРИ
СИСТЕМАТИЧЕСКОМ ИЗЛОЖЕНИИ ГЕОМЕТРИИ
ПРЯМЫЕ ЛИНИИ ОБЫЧНО ПРИНИМАЮТСЯ ЗА
ОДНО ИЗ ИСХОДНЫХ) ПОНЯТИЙ, ИХ СВОЙСТВА
И СВЯЗЬ С ДРУГИМИ ПОНЯТИЯМИ
(НАПРИМЕР, ТОЧКИ И ПЛОСКОСТИ)
ОПРЕДЕЛЯЮТСЯ АКСИОМАМИ ГЕОМЕТРИИ И
ОТНОСИТСЯ К ЧИСЛУ ДРЕВНЕЙШИХ
ГЕОМЕТРИЧЕСКИХ ФИГУР

3. Прямые на плоскости могут пересекаться, совпадать или не пересекаться вообще. При пересечении прямые образуют смежные и

вертикальные углы,
Сумма двух смежных углов равна 180 градусам, а
вертикальные углы равны между собой. Самый
простой пример пересекающихся прямых - это буква
«Х». При таком пересечении образуются, в основном,
два острых угла и два тупых.
Также прямые могут пересекаться и под прямым
углом – тогда их называют перпендикулярными и
при этом образуется четыре прямых угла в точке
пересечения. Пример такого пересечения – значок
«+». Для них есть условное обозначение – значок
перпендикуляра – «⊥».

4. Свойства перпендикулярных прямых:

Из любой точки, не лежащей на данной прямой,
можно опустить перпендикуляр на эту прямую и
притом только один. Соответственно углы будут
равны 90 градусам.

5. Свойства перпендикулярных прямых:

Перпендикуляр из точки к прямой – это
отрезок, соединяющий точку с прямой, и
перпендикулярный к этой прямой. Наклонных
перпендикуляров может быть множество, а
вертикальный- только один.

6.

Для построения перпендикуляров нам, обычно,
требуется транспортир, но иногда проще бывает
воспользоваться чертежным угольником,
имеющим прямой угол.

7. Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжали.

Соответственное правило есть и для
отрезков - Отрезки называются параллельными, если
они лежат на параллельных прямых. Для таких
прямых тоже есть условное обозначение – значок
параллельности – «ll».
Существует аксиома параллельных прямых, которая
звучит: «через точку, не лежащую на данной
прямой, проходит только одна прямая,
параллельная данной.» Это правило, которое не
требует доказательства.

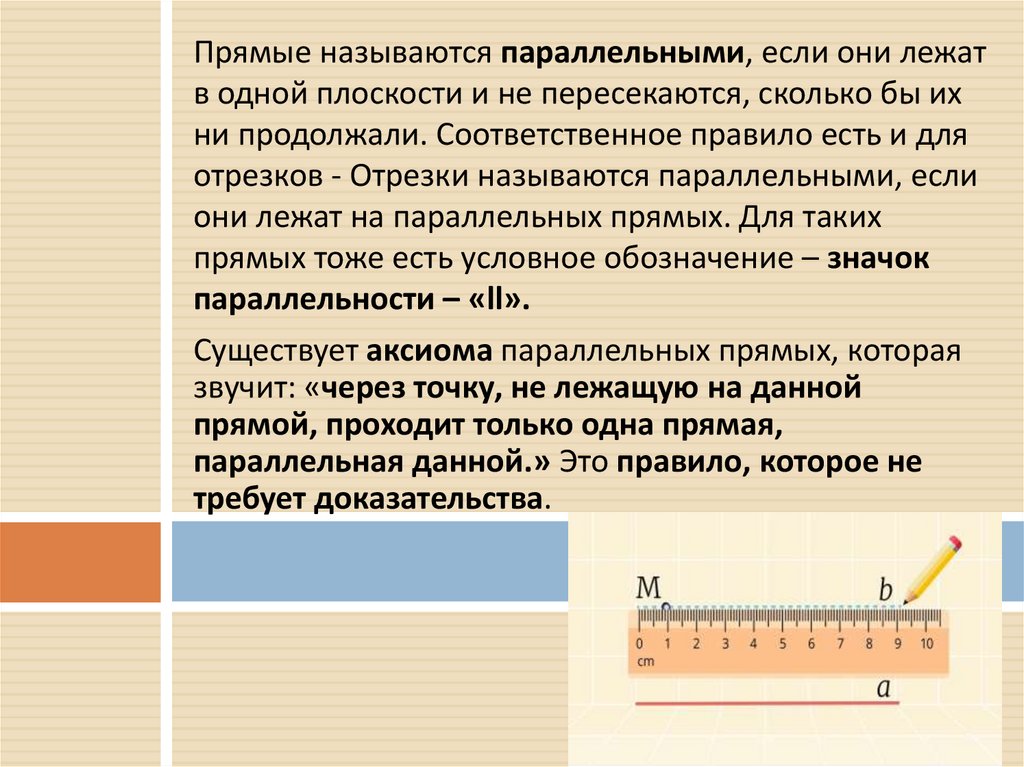
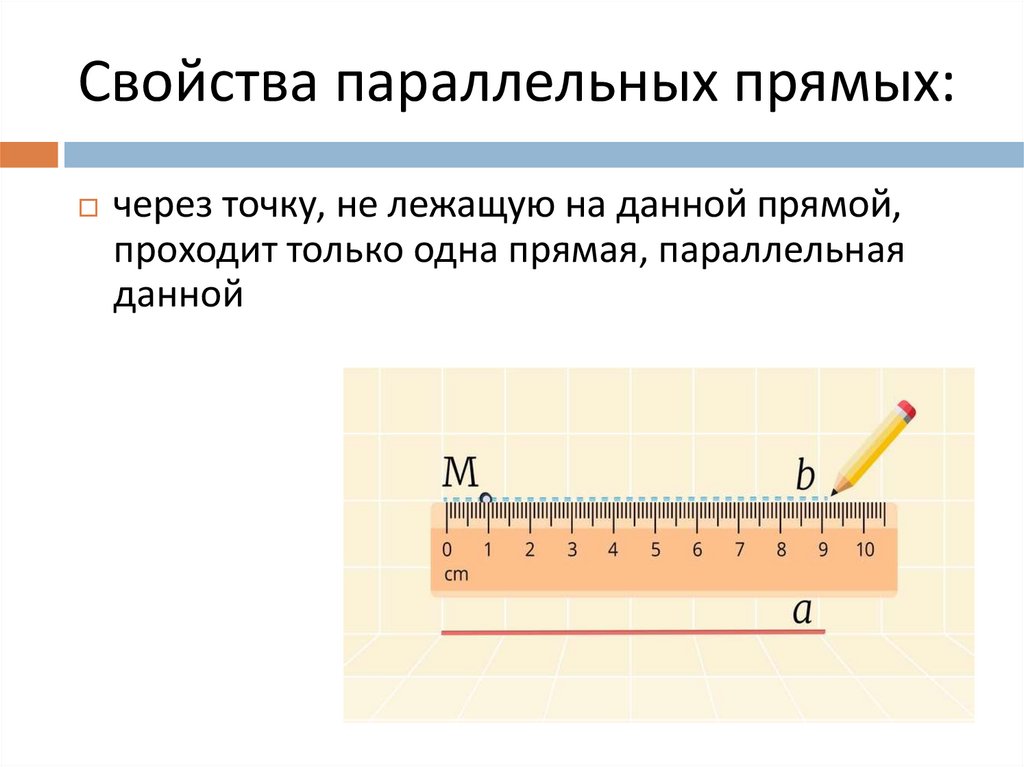
8. Свойства параллельных прямых:

через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная
данной

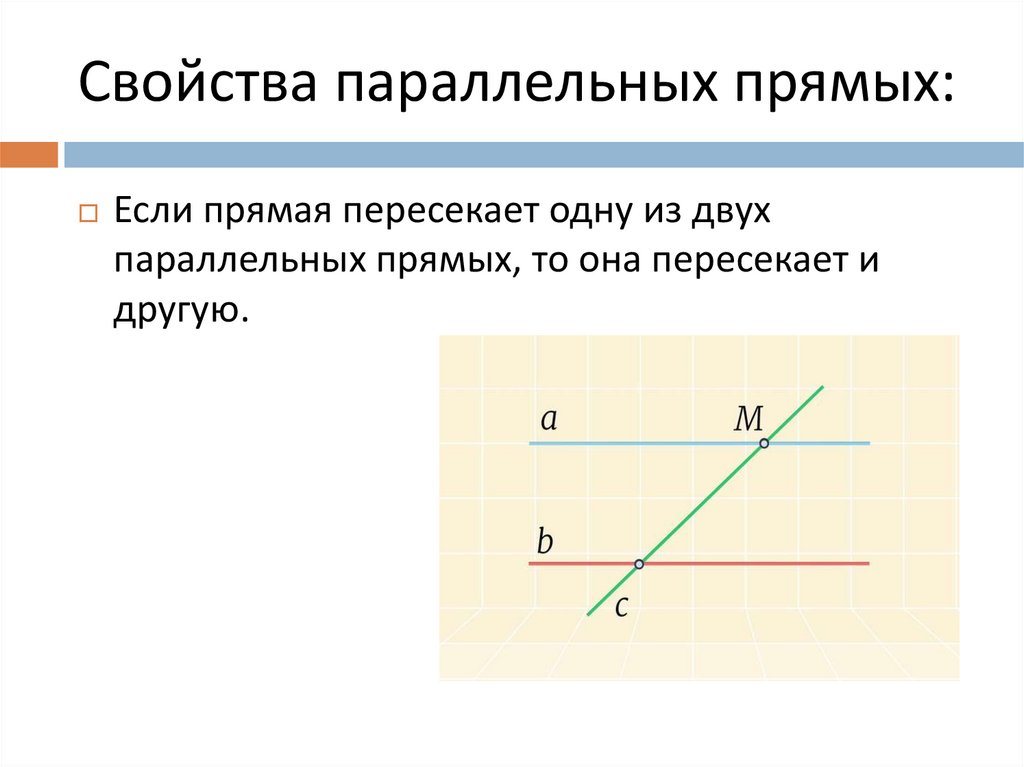
9. Свойства параллельных прямых:

Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и
другую.

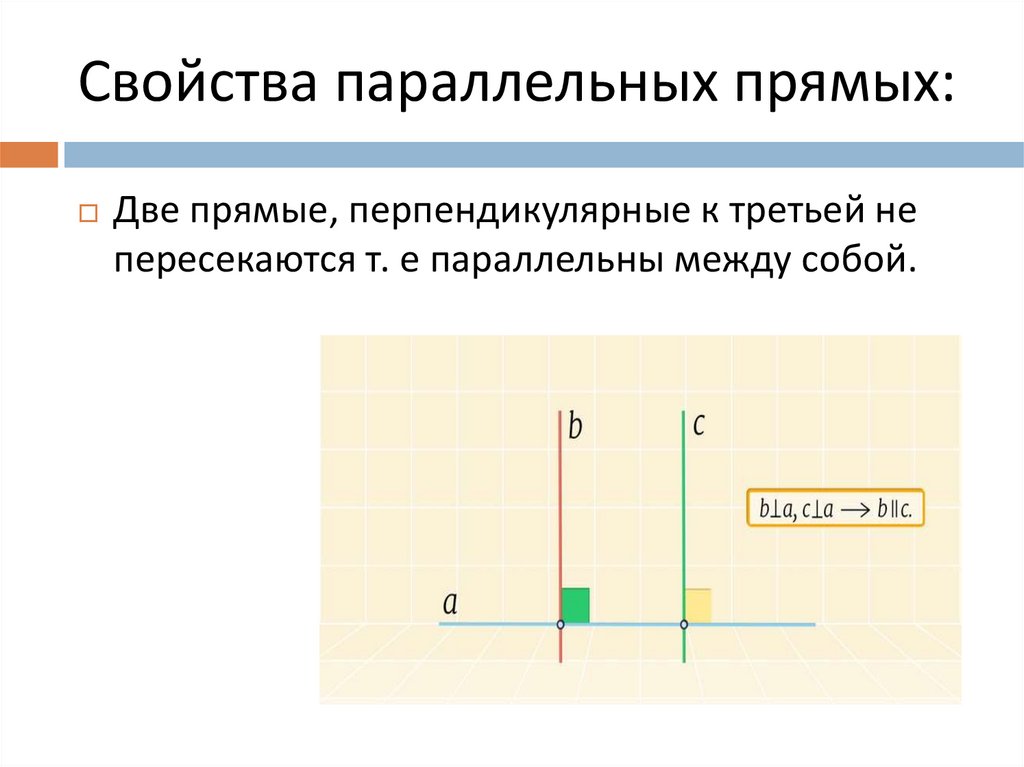
10. Свойства параллельных прямых:

Две прямые, перпендикулярные к третьей не
пересекаются т. е параллельны между собой.

11. Свойства параллельных прямых:

Если две прямые параллельны третьей, то они
параллельны

12. Расстояние – это длина отрезка. Расстояние от точки до прямой можно узнать, посчитав длину перпендикуляра, соединяющего

заданную точку с прямой.
Также легко найти Расстояние
между параллельными прямыми
— это длина перпендикуляра,
соединяющего эти прямые .

13.

Спасибо
За
внимание