Similar presentations:
Преобразование подобия
1.
Преобразованиеподобия
Выполнила
ученица 11а класса
Ширяева Анастасия
2.
евклидовапространства, при
котором для любых двух
точек A, B и их образов
A', B' имеет место
соотношение | A'B' | = k
| AB | , где k —
положительное число,
называемое
коэффициентом
подобия.
3.
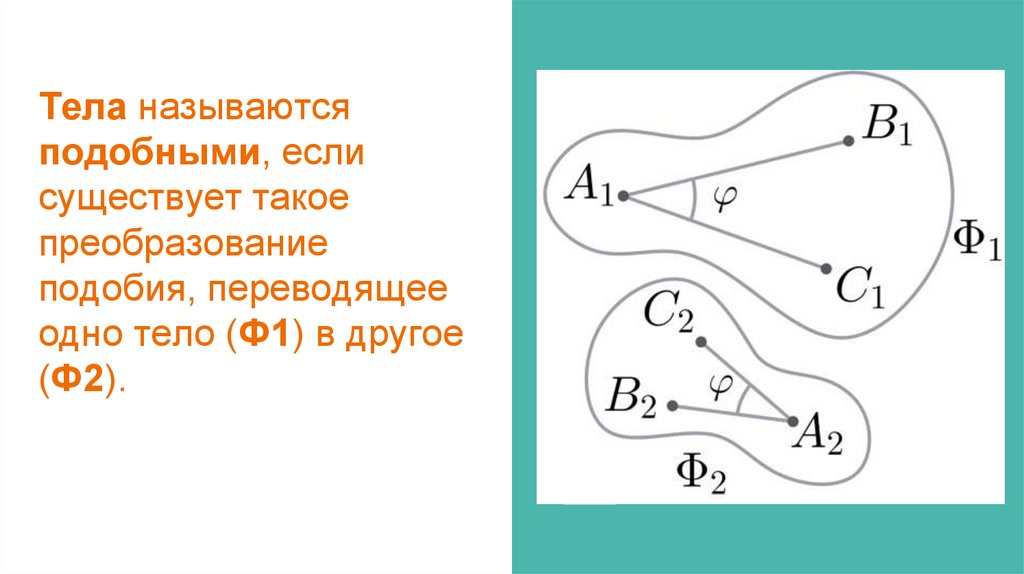
Тела называютсяподобными, если
существует такое
преобразование
подобия, переводящее
одно тело (Ф1) в другое
(Ф2).
4.
Примерыпреобразования
подобия
5.
На практике подобныефигуры можно
получить, например,
поместив под лампой
вырезанную из куска
картона фигуру F,
плоскость которой
параллельна
поверхности стола; в
таком случае тень F',
отбрасываемая этой
фигурой на стол,
будет подобна фигуре
6.
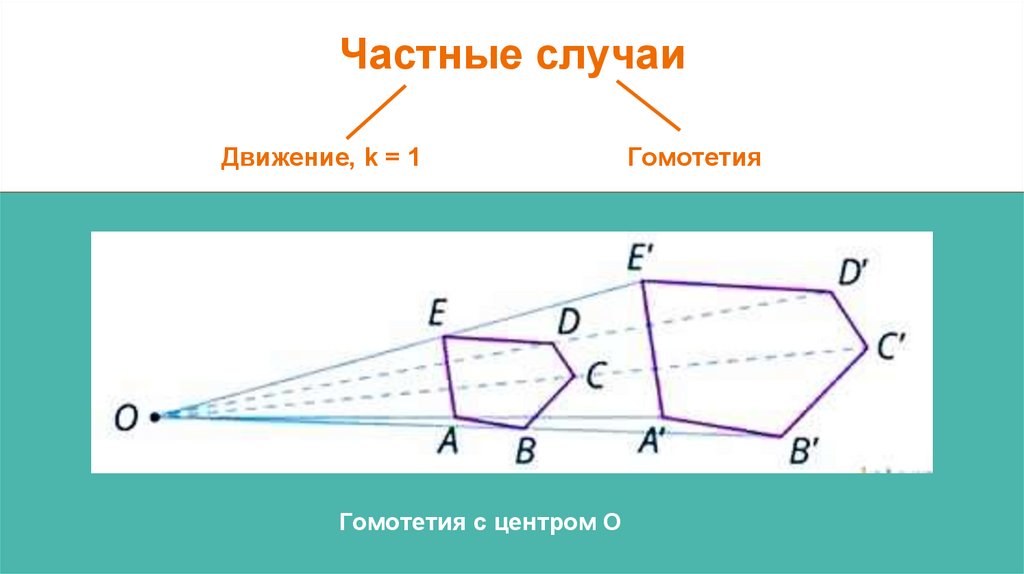
Частные случаиДвижение, k = 1
Гомотетия с центром О
Гомотетия
7.
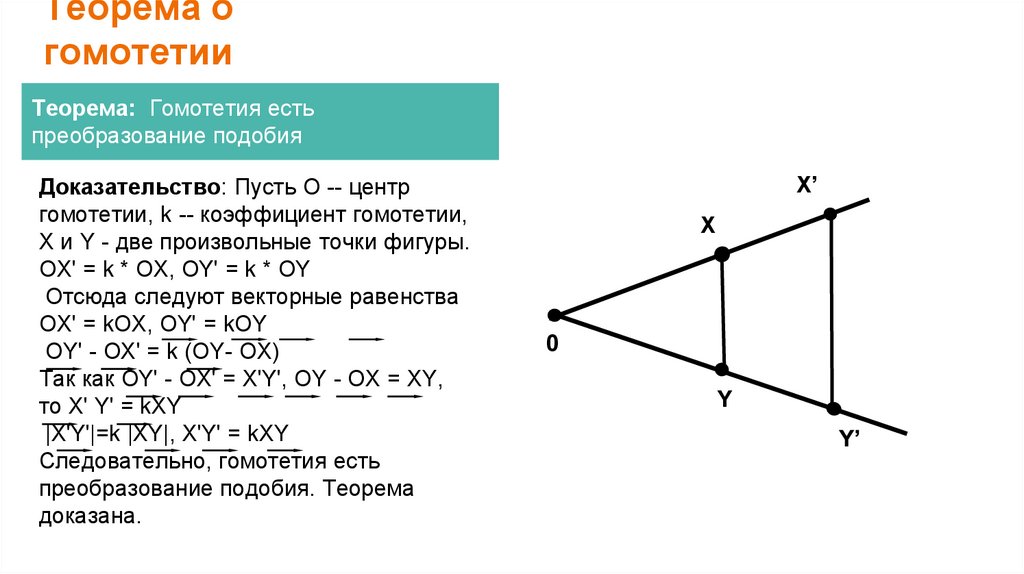
Теорема огомотетии
Теорема: Гомотетия есть
преобразование подобия
Доказательство: Пусть О -- центр
гомотетии, k -- коэффициент гомотетии,
X и Y - две произвольные точки фигуры.
OX' = k * OX, OY' = k * ОY
Отсюда следуют векторные равенства
ОХ' = kOX, OY' = kOY
OY' - OX' = k (OY- OX)
Так как OY' - OX' = X'Y', OY - OX = XY,
то Х' Y' = kХY
|X'Y'|=k |XY|, X'Y' = kXY
Следовательно, гомотетия есть
преобразование подобия. Теорема
доказана.
X’
X
0
Y
8.
При преобразовании подобия углы сохраняютсвою величину.
A2
A
B
C
C
2
A1
B
1
C
Пусть угол ABC преобразованием подобия
с коэффициентом k переводится в угол
А1В1С1.
Подвергнем
угол
ABC
преобразованию гомотетии относительно
его вершины В с коэффициентом гомотетии
k. При этом точки А и С перейдут в точки
А2 и С2. Треугольники А2ВС2 и А1В1С1
равны по третьему признаку. Из равенства
треугольников следует что угол А2ВС2
равен углу А1В1С1. Значит, углы ABC и
А1В1С1 равны, что и требовалось
доказать.
9.
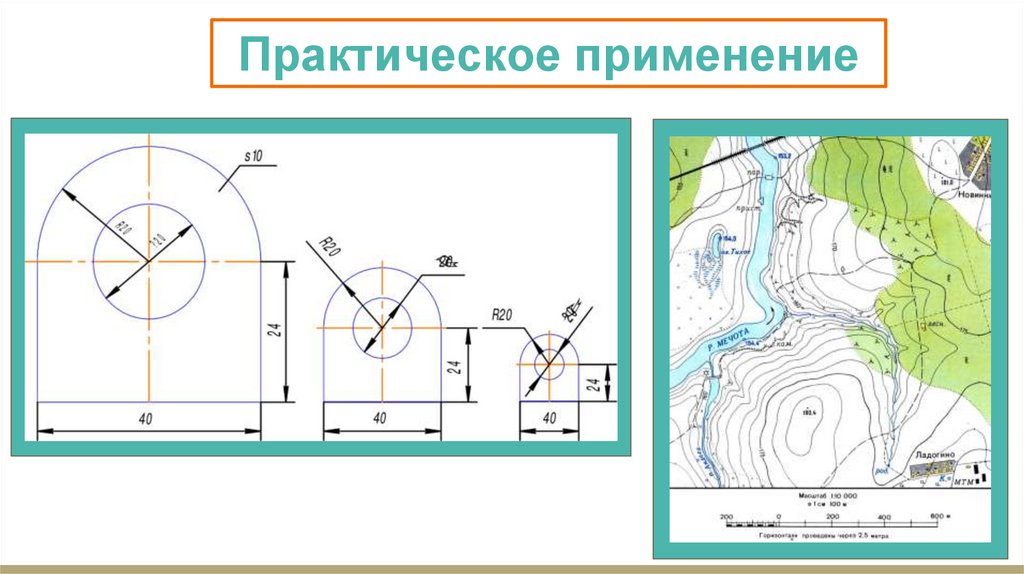
Практическое применение10.
Спасибо завнимание!






 mathematics
mathematics








