1.55M

Category: $mathematics$ mathematics

Решение квадратных неравенств

3.

№1
Решите неравенство:
х 2 5 х 36 0
х 2 7 х 30 0
х 2 4,6 х 2,4 0
2х 7х 6 0
2
2 х 2 50 х 0
4 х 2 49 0
4 х 12 х 9 0
2
х 2 14 х 49 0
5х2 2 х 1 0
9 х 2 30 х 25 0

№1
1)
Решите неравенство:
х 2 5 х 36 0
2)
х 2 7 х 30 0
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох: (–4; 0) и (9; 0)
Ох: (–4; 0) и (9; 0)
х 2 5 х 36 0
х 2 7 х 30 0
х
х
-4
- 10
9
3
х1 х2 5; х1 х2 36 х1 х2 7; х1 х2 30
х1 (–
; хU
х1 4;Ответ:
х2 9) 9
2
(– 4;
∞;10
–10]
Ответ:
[3;3+∞)

5.

№1
3)
Решите неравенство:
х 2 4,6 х 2,4 0
4)
2 х2 7 х 6 0
a < 0 → ветви вниз
a < 0 → ветви вниз
Ох: (0,6; 0) и (4; 0)
Ох: (1,5; 0) и (2; 0)
х 4,6 х 2,4 0х
0,6
4
2
D b 4ac; D 11,56
2
2 х2
7
х
6
0
х
2
2 1,5
D b 4ac; D 1
х1 1,5
х1 0,6
b
D
b
D
Ответ:
U; (4; +∞) х
Ответ:
[1,5;;2]
х12 (– ∞; 0,6)
12
x
4
x2 2
2
2a
2a

6.

№1
5)
Решите неравенство:
2 х 2 50 х 0
6)
4 х 2 49 0
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох: (0; 0) и (25; 0)
Ох:(–3.5; 0) и (3,5; 0)
2 х 50 х 0
4 х 2 49 0
х
0
-3,5
3,5
25 х
2х x 25 0
2x 7 2x 7 0
х1(– ∞;
0;0]
хU2 [25;
25+∞) х1 3,5;(–Ответ:
2 3,5
Ответ:
3,5;х3,5)
2

7.

№1
7)
Решите неравенство:
4 х 2 12 х 9 0
8)
х 2 14 х 49 0
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох: (1,5; 0)
Ох: (7; 0)
4 х 12 х 9 0
2
2 x 3 1,5 0 х
х Ответ:
1,5U (1,5; +∞)
(– ∞; 1,5)
2
х 14 х 49 0
2
x 7 7 0
х(– Ответ:
7 +∞)
∞;
2
х

8.

№1
9)
Решите неравенство:
5х2 2 х 1 0
10)
9 х 2 30 х 25 0
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох: НЕТ
Ох: НЕТ
5х 2 х 1 0
2
D b 4ac; D 0 х
нет корней
(–Ответ:
∞; +∞)
2
9 х 30 х 25 0
2
D b 4ac; D 0 х
нетНет
корней
Ответ:
решений
2

9.

№2
Решите неравенство:
х2 9
х2 5
5 х 2 10 х
3 х 2 75
0,6 х 18 x
2
7 х 2 28

10.

№2
Решите неравенство:
1)
2)
х2 9
х2 5
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох: (–3; 0) и (3; 0)
5 ;0 и 5 ;0
Ох:--------------------
х 9 0
-3
3
x 3 х 3 0
х1 3;Ответ:
х23] 3
[– 3;
2
х
х2 5 0
х
5
5
x 5 x 5 0
х1 ; 5Ответ:
;5 х 2 5 ; 5

11.

№2
3)
Решите неравенство:
4)
5 х 2 10 х
3 х 2 75
a < 0 → ветви вниз
a < 0 → ветви вниз
Ох: (0; 0) и (2; 0)
Ох: (–5; 0) и (5; 0)
5 х 20 10 х 2 0
5х х 2 0
х1 0;Ответ:
2 2
[0;x2]
х
х-52 25 5
x 5 x 5 0
х
х1(–∞;
5–5)
; U
x2 (5;
5+∞)
Ответ:

12.

№2
5)
Решите неравенство:
6)
0,6 х 2 18 x
7 х 2 28
a > 0 → ветви вверх
a < 0 → ветви вниз
Ох: (–30; 0) и (0; 0)
2; 0 и 2 ;0
Ох:--------------------
0,6 х 2 18 x 0
-30
0
0,6x х 30 0
х1 30(–Ответ:
; 30;
х2 0)
0
х
7 х 2 28
х
2
22
x 4
х1 2;; Ответ:
2 х22; 2

13.

№3
Найдите множество решений
неравенства:
3х 1 х 2 6
3х 1 2 16 1 2 х 2
x 3 x 4
1
5
8
2
3x 11
37 x
10
8
6
2
2

14.

3х 2 5 х 8 0
2
Найдите
D b 4acмножество
; D 121 решений
№3
2
неравенства:
b D х1 2
х12
;
3 2
3х 5 x 8 0
3х 1 2хa 2 6
x2 1
1)
a > 0 → ветви вверх
2
1; 0 и 2 ; 0
Ох:------------------- 3
2
1; 2
Ответ:
3
1
2
2
3
х

15.

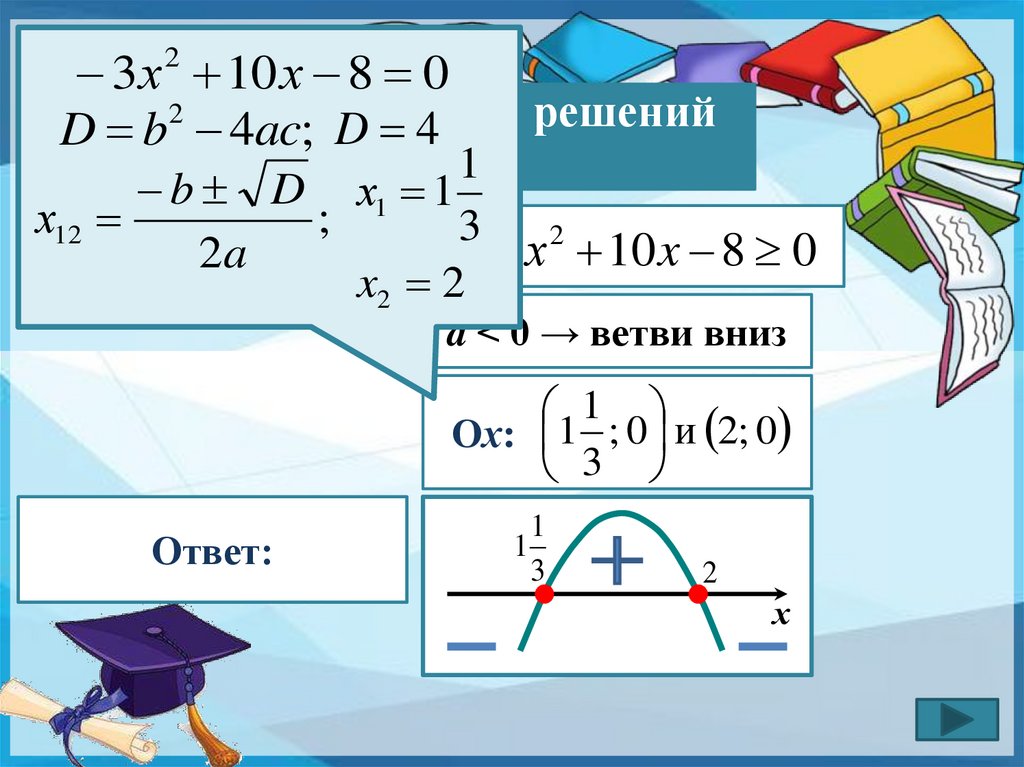
№3 3 х 2
10 х 8 0
2
Найдите
решений
D b 4acмножество
; D 4
1
неравенства:
b D х1 1
х12 2
; 2 3 2
3х 10 x 8 0
2a 1 2 х
3х 1 16
x2 2
2)
a < 0 → ветви вниз
1
Ох:------------------- 1 ; 0 и 2; 0
3
1
Ответ:
1 3 ; 2
1
1
3
2
х

16.

№3 5 х 2
8х 4 0
2
Найдите
D b 4acмножество
; D 144 решений
неравенства:
2
b D х1
х12
;
2
5 5 х 2 8 x 4 0
x 3 2xa 4
1x 2
2
5
8
3)
a < 0 → ветви вниз
2
Ох:------------------- ; 0 и 2; 0
5
2
2;
; Ответ:
5
2
5
2
х

17.

№3
Найдите множество решений
4)
неравенства:
3x 11 х 3725
x
10
8 х 5
6х 5
2
2
2
1
2
5 х 125 0
2
a > 0 → ветви вверх
Ох:--(–5; 0) и (5; 0)
Ответ:
(–5;
5)
5
5
х

18.

№4
Найдите целые решения
неравенства:
х 6х 0
2
0,25 х 3х 7 0
2
х 2 2,6 х 1,2 0
6 х2 7 х 2 0

19.

№4
1)
Найдите целые решения
неравенства:
2)
х 6х 0
2
0,25 х 3х 7 0
2
a > 0 → ветви вверх
a < 0 → ветви вниз
Ох: (–6; 0) и (0; 0)
14; 0 и 2 ;0
Ох:--------------------
х 6х 0
х х -6 6 0 0
х1 6; х2 0
2
0,25 х 14 3x 7
2
2
0
х
D b 4ac; D 16
х2 2
х1
14
;
–13;Ответ:
–12; … ; 1
2
х
–6;–5;–4;–3;–2;–1;
Ответ:
0

20.

№4
Найдите целые решения
неравенства:
3)
х 2,6 х 1,2 0
2
6 х2 7 х 2 0
a > 0 → ветви вверх
a < 0 → ветви вверх
Ох: (0,6; 0) и (2; 0)
2
; 0 и 0,5 ;0
Ох:------------------- 3
х 2,6 х 1,2 0
х
0,6
2
х1 х2 2,6; х1х2 1,2
х1 0,6;Ответ:
1; 2х2 2
2
4)
2
3
6х 7x 2 0
х
2 0,5
D b 4ac; D 1 2
х2
х1Нет
0целых
,5;Ответ:
решений3
2

21.

№5
Найдите область определения
функции:
у х 3х 40
2
у
х 2
3 х 12 х
2

22.

№5
Найдите область определения
1) х 2 3 х функции:
40 0
х1 х22 3; х1х2 40х 2 3x 40 0
у х 3х 40
х1 8; х2 5
a > 0 → ветви вверх
8; 0 и 5; 0
Ох:--------------------
; Ответ:
8 5;
8
5
х

23.

№5
Найдите область определения
2)
2
функции:
3 х 12 х 0
2
х 42х 0
3
х
1
3x 12 х 0
у
х1 3 х 0 ;12 хх22 0,25
a > 0 → ветви вниз
0; 0 и 0,25; 0
Ох:-------------------Ответ:
(0;
0,25)
х
0
0,25

24.

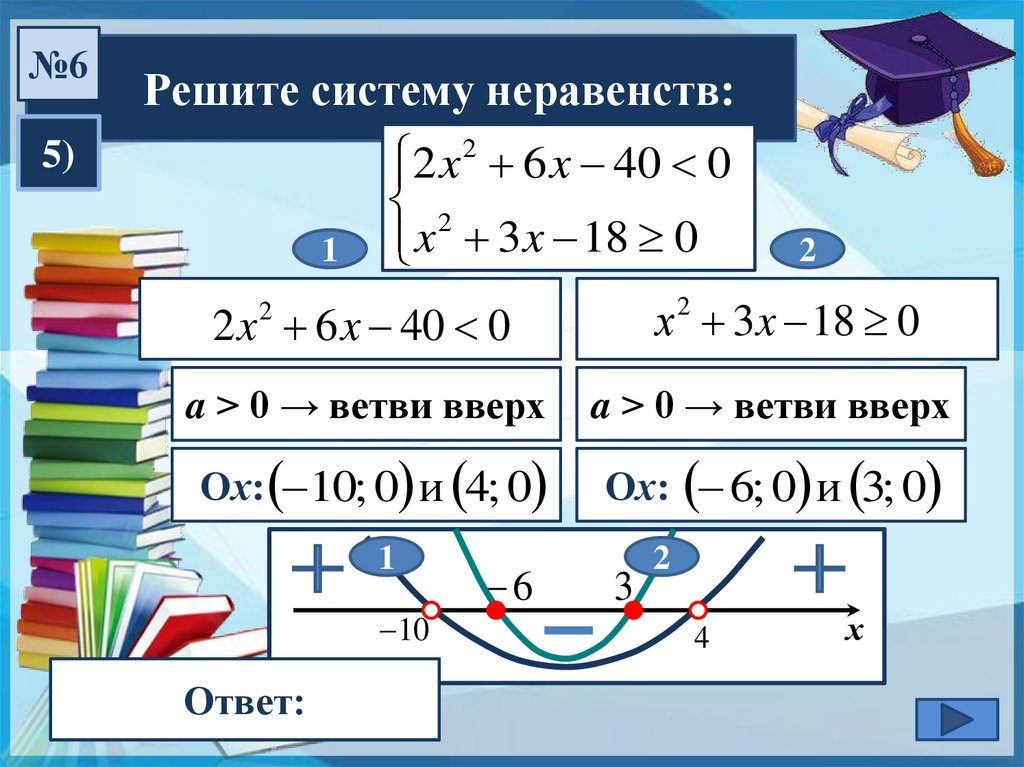
№6
Решите систему неравенств:
x2 x 6 0
x 0
3x 2 8 x 3 0
x 10
2 x 2 13x 7 0
15 3x 0
x 2 x 12 0
8 2 x 0
2
2 x 6 x 40 0
2
x 3 x 18 0
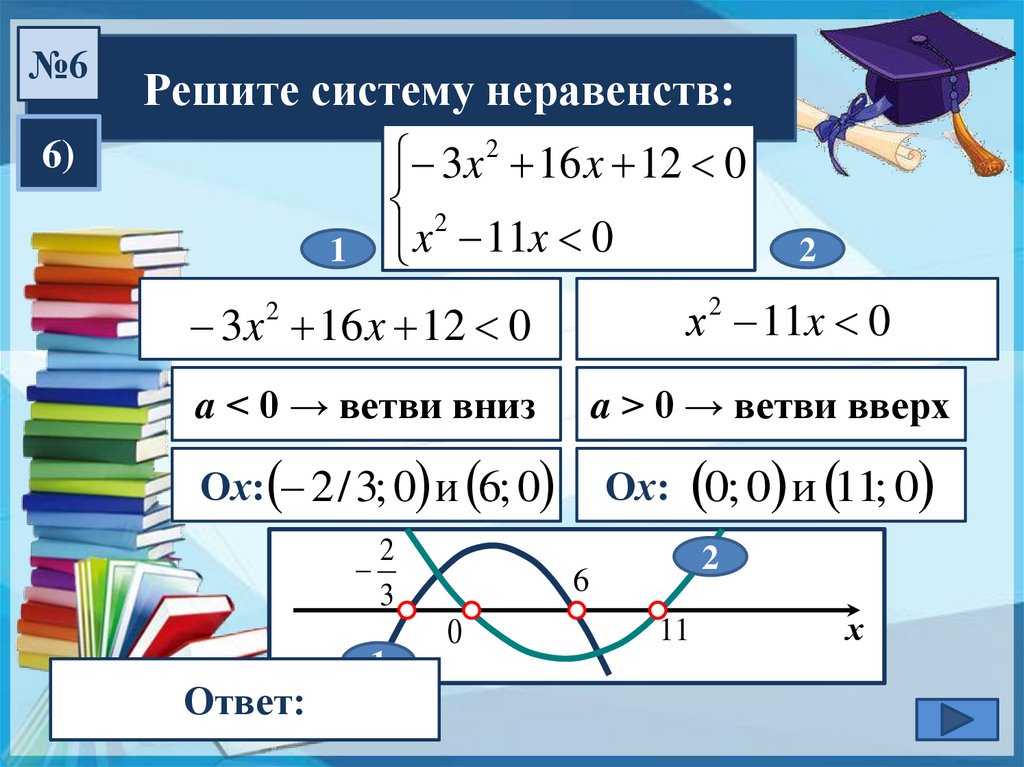
3x 2 16 x 12 0
2
x 11x 0

25.

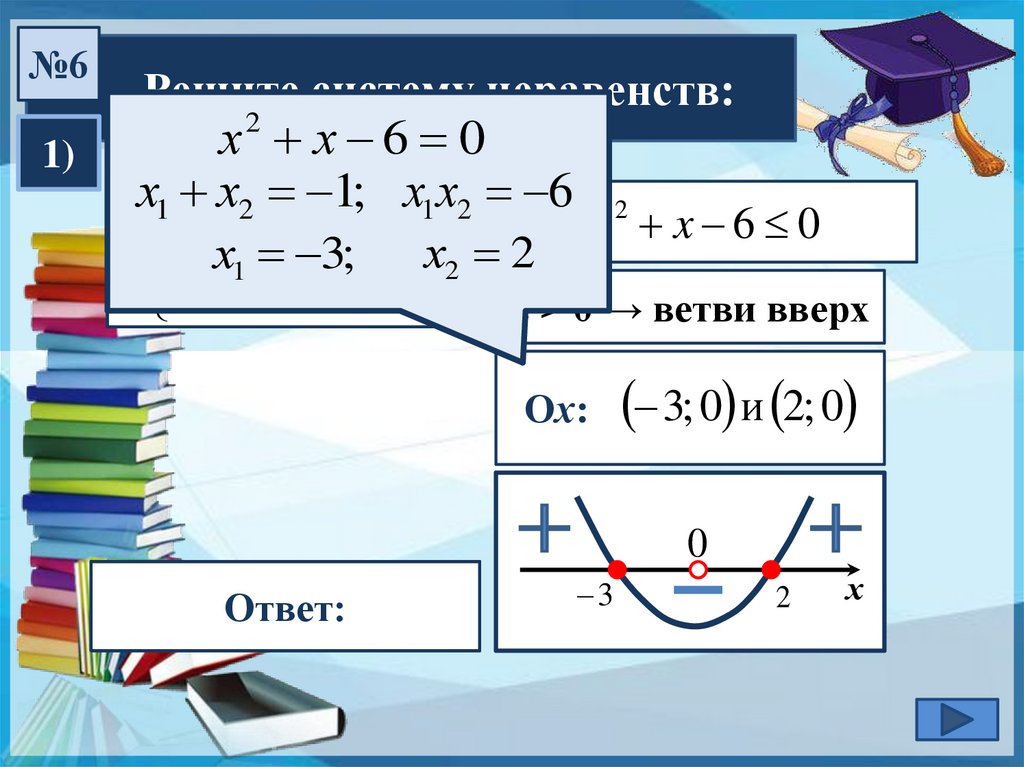
№6
Решите систему неравенств:
х х 6 0
х1 2 х2 1; х1х2 6
2
1)
2
x x 6 0
х x 6 0
х1 3; х2 2
x 0
a > 0 → ветви вверх
3; 0 и 2; 0
Ох:--------------------
Ответ:
0; 2
0
3
2
х

26.

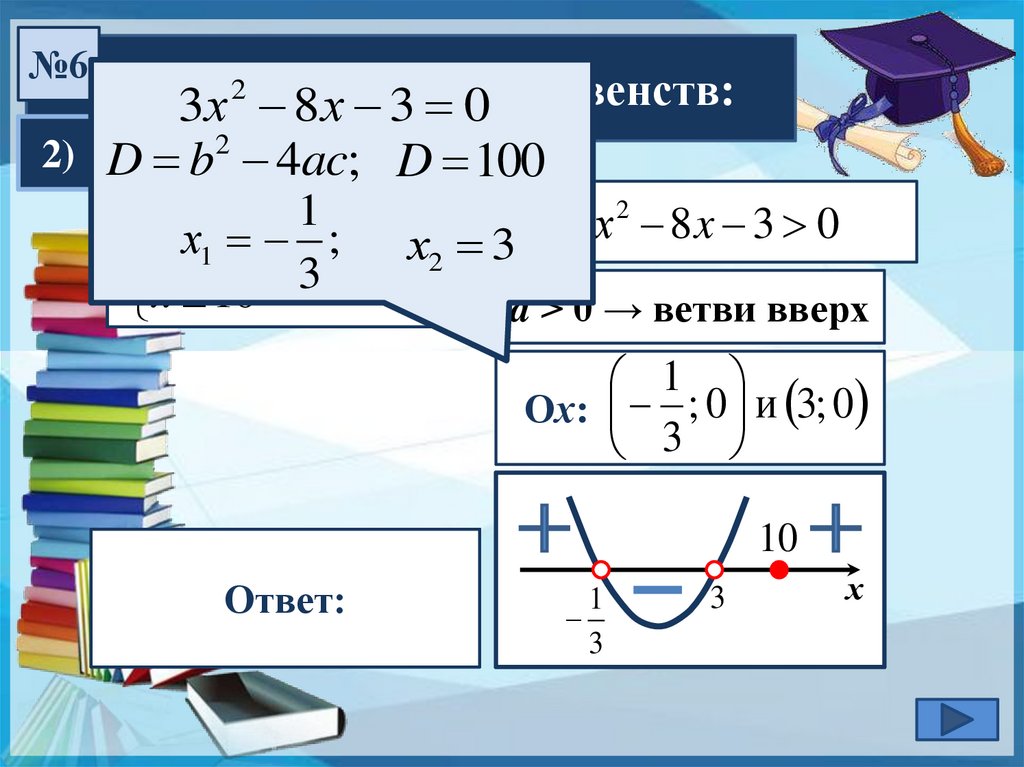
№6
2)
2
Решите
3х 8систему
х 3 0неравенств:
D b 4ac; D 100
2
2
3xх2 8 x 1 ;3 0
3х 8 x 3 0
х
3
2
1
3
x 10
a > 0 → ветви вверх
1
; 0 и 3; 0
Ох:------------------- 3
1
; Ответ:
3; 10
3
10
1
3
3
х

27.

№6
3)
Решите систему неравенств:
2 х 2 13 х 7 0
2
2
2
D
2 x b13 x4 ac
7 ; 0D 2252 х 13 x 7 0
х31x 07; х2 0,5
15
a > 0 → ветви вверх
15 3x 0
x 5
7; 0 и 0,5; 0
Ох:-------------------5
НЕТОтвет:
решений
7
0,5
х

28.

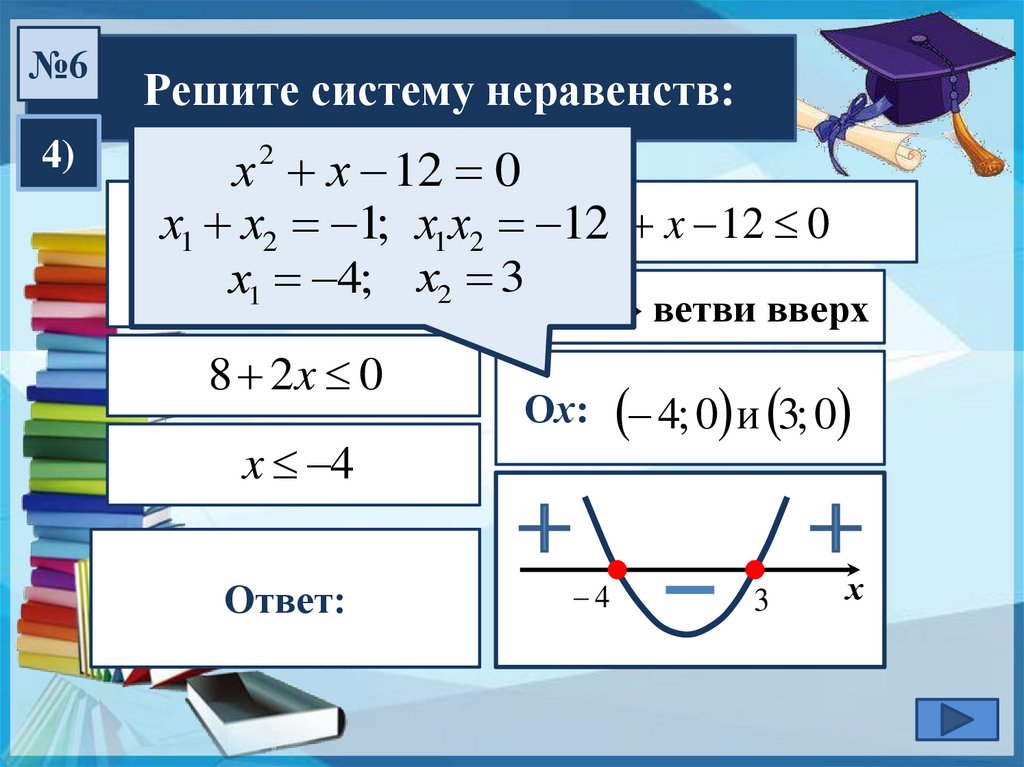
№6
4)
Решите систему неравенств:
х 2 х 12 0
2
хx12 хx2 12 1;0 х1х2 12
х x 12 0
хx1
4; х2 3
8
2
0
a > 0 → ветви вверх
8 2x 0
Ох:------------------- 4; 0 и 3; 0
x 4
Ответ:
{–4}
4
3
х

29.

№6
Решите систему неравенств:
2 x 6 x 40 0
2
x 3 x 18 0
2
5)
1
2
х 3x 18 0
2 x 6 x 40 0
2
2
a > 0 → ветви вверх
a > 0 → ветви вверх
Ох:------------------- 10; 0 и 4; 0
Ох:------------------- 6; 0 и 3; 0
1
10
(–10; Ответ:
–6] U [3; 4)
6
3
2
4
х

30.

№6
Решите систему неравенств:
3x 16 x 12 0
2
x 11x 0
2
6)
1
2
х 11x 0
3x 16 x 12 0
2
2
a < 0 → ветви вниз
a > 0 → ветви вверх
Ох:------------------- 2 / 3; 0 и 6; 0
Ох:------------------- 0; 0 и 11; 0
2
3
6
0
Ответ:
(6;
11)
1
2
11
х

31.

№7
Найдите, при каких значениях а
не имеет корней уравнение:
x a 2 x 4 0
2
a 1 x2 3ax 4a 0
10 2a x a 5 x 1 0
2
a 1 x2 2 a 1 x 3a 3 0

32.

№7 Найдите, при каких значениях а
1)
не имеет
корней уравнение:
2
a 4a 12 0
a
21 a2 4; a1a2 122
a 4a 12 0
x a 2 x 4 0
уравнение не
2
a1 6; а2 Квадратное
имеет
корней,
если
2
ветви
вверх
D a 4a 12
дискриминант меньше нуля!
( D6;<0 0и) 2; 0
Оa:--------------------
Ответ:
6; 2
6
2
a

33.

№7 Найдите, при каких значениях а
2)
не имеет
корней уравнение:
2
a 2a 15 0
a1 2 a2 2; a1a2 152
a 2a уравнение
15 0 не
10 2a x a a 53 ;x 1a 0Квадратное
5
2
1
имеет корней, если
ветви вверх
D a 2a 15дискриминант
меньше нуля!
( D3;<0 0и) 5; 0
Оa:-------------------2
Ответ:
3; 5
3
5
a

34.

№7 Найдите, при каких значениях а
3)
не имеет2 корней уравнение:
a 1 x
2
a a 2 0
D 9
a уравнение
a 2 0 не
2 a 1 x 3a 3 Квадратное
0
a1 2; a2 1
имеет корней, если
2
Ветви вниз
D a a дискриминант
2
меньше нуля!
2
( D
2<; 00 )и 1; 0
Оa:--------------------
; Ответ:
2 1;
2
1
a

35.

№7 Найдите, при каких значениях а
4)
не имеет корней уравнение:
2
a
7
a
16
0
7a 16
a 0 не
a 1 x 3ax 4a 0Квадратное
уравнение
2
2
a2 2
a1 0;2
имеет
корней,
если
ветви
вниз
7
D 7 a 16a
дискриминант меньше нуля!
( D2< 0 )
Оa:------------------- 2 ; 0 и 0; 0
7
2
; 2Ответ:
0;
7
2
2
7
0
a

36.

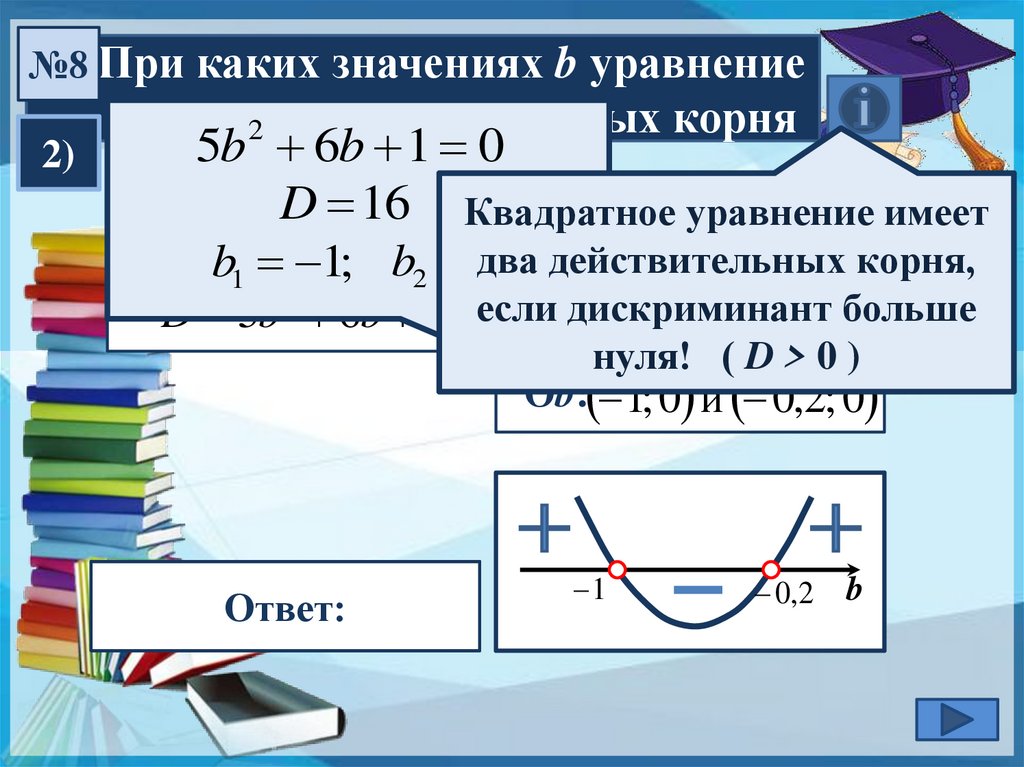
№8
При каких значениях b уравнение
имеет два действительных корня
x 4bx 3b 1 0
2
bx 3b 1 x b 0
2
b 1 x
2
2 b 1 x 3b 2 0
3b 2 x 5b 2 x 5b 1 0
2

37.

№8 При каких значениях b уравнение
1)
имеет два
действительных корня
2
4b 3b 1 0
2
D
25
2
Квадратное
4b 3bуравнение
1 0 имеет
x 4bx 3b 1 0
два
1 действительных корня,
b1 0,25; b2
ветви вверх больше
D 4b 2 3b 1 если дискриминант
нуля! ( D > 0 )
Оb:------------------- 0,25; 0 и 1; 0
; - Ответ:
0,25 1;
0,25
1
b

38.

№8 При каких значениях b уравнение
2)
имеет два
действительных корня
2
5b 6b 1 0
2
2
D
16
Квадратное
5b 6bуравнение
1 0 имеет
bx 3b 1 x b 0
0,2действительных корня,
b1 1; b2 два
ветви вверх больше
D 5b 2 6b 1 если дискриминант
нуля! ( D > 0 )
Оb:------------------- 1; 0 и 0,2; 0
; 1Ответ:
0,2;
1
0,2
b

39.

№8 При каких значениях b уравнение
имеет два действительных корня
4b 2 3b 3 0
2
2
Квадратное
4b 3bуравнение
3 0 имеет
b 1 x 2 b 1D x 3 b37
2 0
3)
нет2 корней два действительных корня,
ветви вверх больше
D 4b 3b 3 если дискриминант
нуля! ( D > 0 )
Оb:-------НЕТ---------
Ответ:
;
b

40.

№8 При каких значениях b уравнение
4)
2
имеет
два
корня
35b действительных
72b 4 0
D 4624
2
Квадратное
2
b 4 0 имеет
3b 2 x b5b 2 x ;5b 1 b 0 2 35b 72уравнение
2 два действительных корня,
1
35
ветви вниз больше
D 35b 2 72b 4 если дискриминант
2
нуля! ( D > 0 )
2
; 0 и 2; 0
Оb:------------------- 35
2
; 2
Ответ:
35
2
35
2
b

41.

Титульный слайд
Магистр
Шапочка выпускника
Школьные учебники-1
Школьные учебники-2
Школьные учебники - 3

English Русский Rules