Similar presentations:
Физические основы прочности
1. Лекция 3 Физические основы прочности
Теории деформационного упрочненияметаллов
1
2.
Наблюдаемые малые значения напряжения началатечения
металлических
кристаллов
связаны
с
перемещением дислокаций. Поэтому справедливо
полагать, что
последующее упрочнение происходит
вследствие затруднения движения дислокаций через
кристалл. Для продолжения деформации требуется
приложение больших напряжений. Движению дислокаций
препятствует ряд различных факторов, важнейшими из
которых являются следующие:
1) другие дислокации;
2) границы зёрен и субзёрен;
3) атомы растворенных веществ;
4) частицы второй фазы;
5) поверхностные пленки.
2
3.
Известно, что монокристаллы даже очень чистых металловзаметно упрочняются при деформации, то становится
очевидным, что другие дислокации являются наиболее
важными препятствиями. Поэтому этот фактор упрочнения,
необходимо рассмотреть в первую очередь.
Представляется
логичным
рассмотреть
последовательность
формирования
подходов
для
описания деформационных процессов на первой, второй и
третьей стадиях деформационного упрочнения. Из теории
дислокаций
следует,
что
когда
две дислокации
приближаются друг к другу, возникает притягивающее или
отталкивающее упругое взаимодействие. Понятие об этом
взаимодействии
лежит
в основе
ранних
общих
дислокационных теорий упрочнения.
3
4.
2. Ранние теорииПервая общая теория упрочнения, оперирующая
дислокационными представлениями, была предложена
Тейлором в 1934 г. К этому времени было, установлено, что
кривые деформации металлических
кристаллов, таких, как алюминий, в первом приближении
можно считать параболическими; это
учитывалось моделью Тейлора.
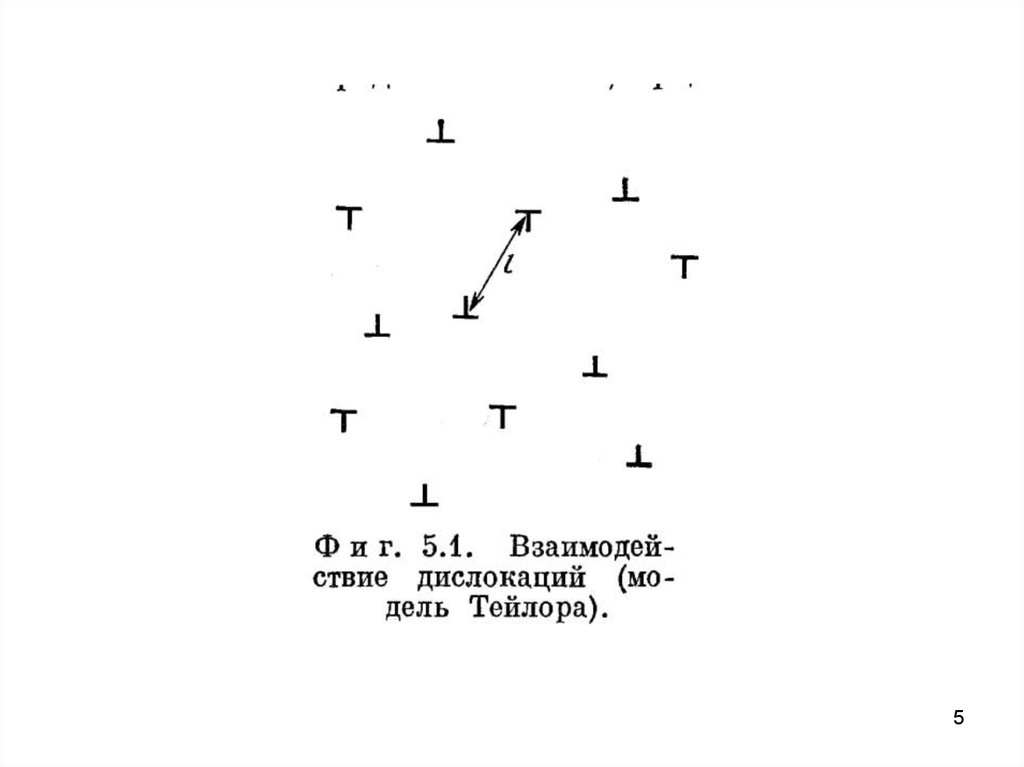
В этой модели принято, что многие дислокации не достигают
поверхности кристалла, упруго взаимодействуя с другими
дислокациями, закрепляются внутри кристалла, образуя сетку
(рис. 5.1). Такой процесс непрерывно развивается по мере
продолжения деформации, и концентрация дислокаций
постепенно увеличивается, а напряжение, необходимое для
продвижения последующих сдвигов дислокаций возрастает.
4
5.
56.
Расстояние между дислокациями I равно1/ D
и они упруго взаимодействуют с соседними. Эффективное
внутреннее напряжение являющееся результатом этого
взаимодействия, соответствует напряжению, необходимому
для прохождения одной дислокации мимо другой, и
выражается в виде
6
7.
78.
Тейлоррассмотрел
расположение
дислокаций,
образующих трехмерную решетку в кристалле. Скорость
упрочнения
зависит
от
величины
L,
которая,
по
предположению
Тейлора,
определяется
мозаичной
структурой, не позволяющей дислокациям двигаться через
кристалл. Величина L составляет около 10-4 см, и если это
значение подставить в выражение 5.1 для относительно
больших деформаций, порядка 100%, то плотность
дислокаций получается 1012 см-2, что в общем согласуется с
экспериментальными
по
определениями
данной
характеристики в сильно наклепанных металлах.
8
9.
Модель Тейлора не согласуется с экспериментами в томотношении,
что
деформация
в
действительности
осуществляется не путем перемещения отдельных готовых
дислокаций, а в результате испускания большого их
количества из источников, например типа Франка Рида, и
движения по плоскостям скольжения. Другим возражением
является то, что застопорившие друг друга пары
дислокаций могут продвигаться дальше под воздействием
других дислокаций.
9
10.
Мотт преодолел некоторые из затруднений теорииТейлора, заменив взаимное влияние индивидуальных
дислокаций
взаимодействием
между
группами
дислокаций в плоских скоплениях. Подобные группы он
представлял себе как дислокации, испускаемые из
источника Франка Рида в одной плоскости скольжения
и скапливающиеся у таких препятствий, как сидячие
дислокации (рис. 5.2). Это приводит к увеличению
внутреннего напряжения в голове скопления, что
вызывает действие источников по некоторым вторичным
системам. Дислокации, образующиеся в таких системах,
взаимодействуют с первичными дислокациями в
скоплениях. В результате реакций взаимодействия
дислокации в скоплениях оказываются запертыми при
снятии внешнего напряжения.
10
11.
1112.
Дислокационные скопления можно рассматривать каксверхдислокации с вектором Бюргерса nb, где n число
дислокаций в скоплении; напряжение в голове скопления в
n раз больше приложенного напряжения .
Соответственно расстояние между скоплениями может
быть значительно больше, чем между отдельными
дислокациями в модели Тейлора, и может быть порядка
расстояния
между
полосами
скольжения.
Если
предположить, что дислокации, порождаемые одним
источником, скапливаются по обе стороны от него, так что
общая длина скопления составляет 2L (каждый отрезок
дислокации продвигается на расстояние L), а расстояние
между плоскостями скольжения равно Р, то плотность
групп скоплений равна 1/LP, а среднее расстояние между
ними равно (LP)1/2. Среднее напряжение , создаваемое
каждым скоплением, определяется выражением.
12
13.
Пластическаядеформация
определяется
простым
суммированием деформации от каждого скопления и является
произведением величины nbL на плотность скоплений 1/LP;
отсюда
Комбинируя выражения (5.5) и (5.6), получаем
13
14.
. Более новые теории упрочненияДетальному
рассмотрению
определенных
стадий
упрочнения металлических кристаллов логично предпослать
выяснение вопроса о величине напряжения, необходимого
для первоначального движения дислокаций, т. е. вопроса о
напряжении начала течения. В гл. 3 было показано, что
критические приведенные напряжения сдвига зависят от
определенных важных переменных факторов, одним из
которых является температура. Зегер предположил, что
напряжение начала течения определяется не только
взаимодействием друг с другом первых дислокаций,
возникших на выбранной системе скольжения, но и их
взаимодействием с дислокациями, существовавшими в
отожженном металле. По-видимому, эти дислокации «роста»
распределены
случайно и многие из них пересекают
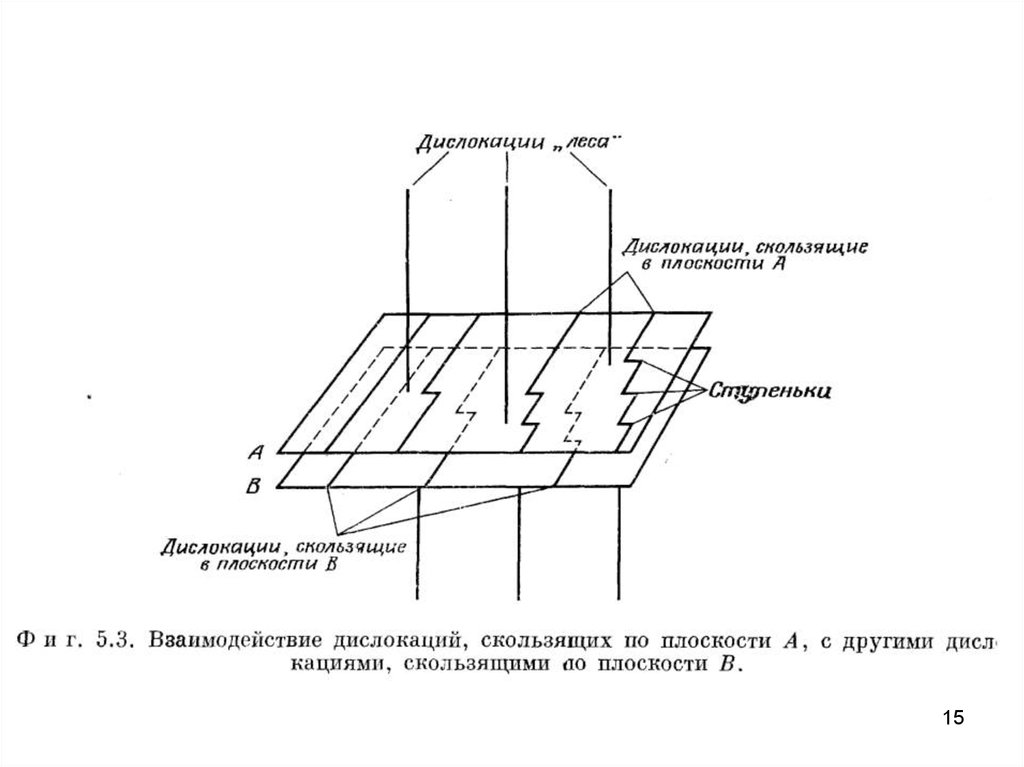
первичные плоскости скольжения. На рис. 5.3 показана
идеализированная модель, в которой имеются скользящие
дислокации в двух соседних полосах скольжения 14 и
некоторые дислокации «леса».
15.
1516.
1617.
1718.
• Первая стадия упрочнения18
19.
Предполагается, что имеется N источников дислокаций наединицу объёма, каждый из которых испускает n
дислокационных петель по достижении напряжения .
Каждая дислокационная петля перемещается на большое
расстояние L через кристалл, тогда как петли на
примыкающих плоскостях скольжения расположены на
расстоянии d друг от друга, значительно меньшем, чем L.
Возрастание напряжения происходит в результате
увеличения числа петель на n, что приводит к
увеличению деформации на величину ,
которая
выражается в виде
19
20.
Величину N также можно определить через d и L:так что
1
N 2
dL
b n
d
Gb n
B
2 L
20
21.
2122.
• Вторая стадия упрочненияНаиболее
значительная
доля
упрочнения
в
гранецентрированных кубических металлах приходится на
вторую стадию, которая подобно первой стадии линейна, но
характеризуется значительно большим коэффициентом
упрочнения, приблизительно равные 2 10-3G (см., например,
рис. 4.13). Кроме того, этот коэффициент на второй стадии
относительно
независим
от
температуры.
Кривые
деформации различаются тем, что при повышении
температуры третья стадия, или стадия параболического
упрочнения, начинается раньше. Поэтому протяженность
второй стадии сокращается. Это показывает, что сильное
увеличение напряжения течения на второй стадии связано
преимущественно с температурнонезависимым вкладом от
полей напряжений дислокаций на первичных плоскостях
скольжения, а не с компонентой, относящейся к
взаимодействию с «лесом» дислокаций, которая зависит 22
от
23.
Наблюдения линий скольжения на второй стадиипоказывают, что они становятся все более коротким. Это
является результатом увеличения концентрации барьеров
Ломер — Коттрела.
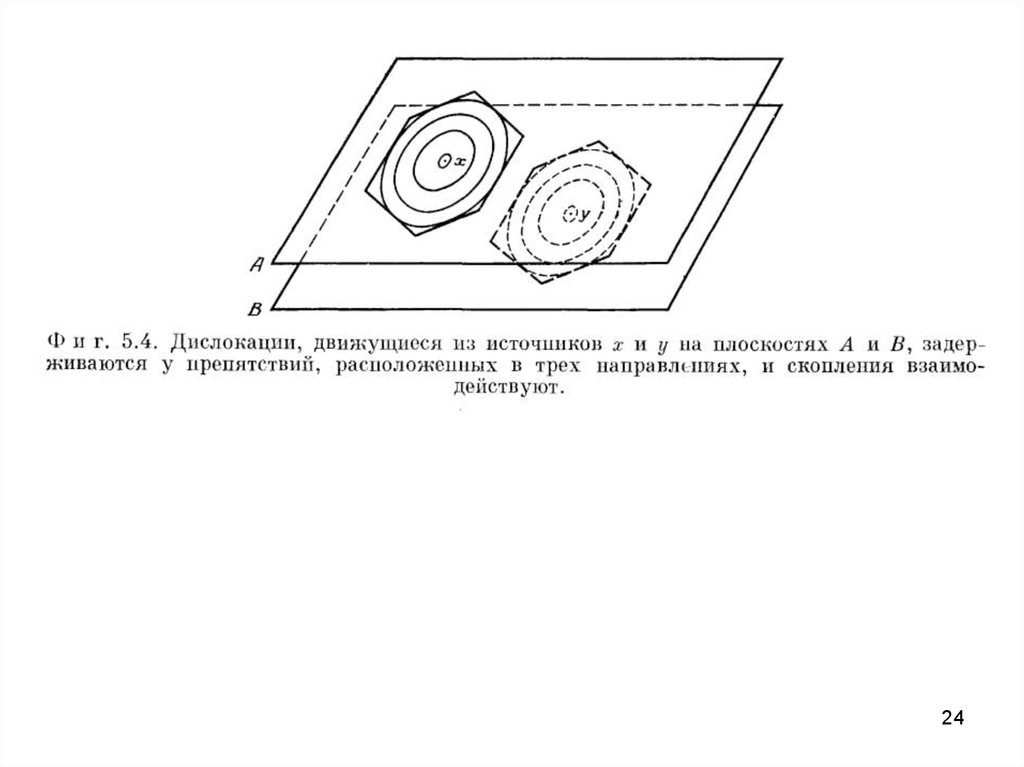
Считается, что дистанция скольжения дислокаций в
скоплении постоянна, но число дислокаций в каждом
скоплении пропорционально напряжению. Дислокации
генерируются источниками Франка Рида. Упрочнение
возникает благодаря дальнодействующим напряжениям от
этих скоплений дислокаций, которые взаимодействуют
друг с другом (рис. 5.4).
23
24.
2425.
Если в каждом скоплении имеется n дислокаций и полное числотаких скоплений в единице объема составляет N, а длина линий
скольжения принимается постоянной и равна R, то получаем
следующее выражение' для деформации:
= N R2nb
(5.18)
Для расчета напряжения группы дислокаций в скоплениях
принимаются за сверхдислокации. Такие группы находятся друг
от друга на расстоянии
1
l
2NR 1/ 2
Тогда
напряжение , требуемое для движения дислокации через
R
bG напряжений, определяется выражением
поле
n k
1 Gbn
2 l
Число дислокаций в скоплениях зависит от напряжения согласно
основному соотношению Эшелби, Франка и Набарро
n k
R
bG
25
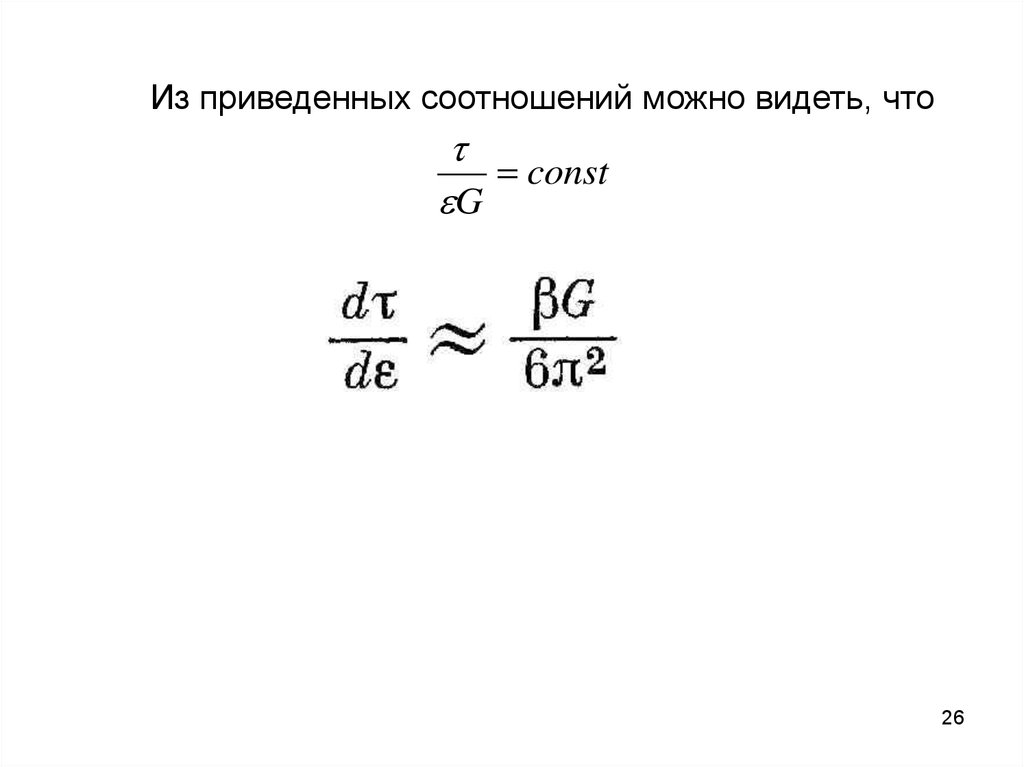
26.
Из приведенных соотношений можно видеть, чтоconst
G
26
27.
Попытка дальнейшего развития теории второй стадииупрочнения гранецентрированных кубических металлов
принадлежит Мотту, который так же основывался на том,
что в этом процессе температура не играет значимой роли.
Дополнительно он принял следующие три положения:
1. Процесс в монокристаллах и поликристаллах протекает
сходным образом.
2. Отношение (d /d )/G мало отличается при переходе от
одного кристалла к другому. Это отношение приближенно
равно 0.03, но может изменяться вдвое в зависимости от
изменения ориентировки.
3. На второй стадии упрочнения линии скольжения
значительно короче, чем на первой стадии, и их средняя
длина уменьшается с увеличением деформации.
27
28.
Мотт не согласился с теорией Зегера по несколькимпричинам.
Во-первых, следует ожидать, что большие напряжения в
голове скоплений должны рассасываться вследствие
скольжения по другим системам, и в любом случае трудно
объяснить, почему скопления дислокаций не стекают
обратно в источник при снятии внешних напряжений. Кроме
того, должен существовать механизм, объясняющий
стремительное
образование
полос
скольжения,
наблюдаемое на поверхности деформируемого кристалла,
а также сложные сплетения дислокаций, которые
обнаруживаются методом электронной микроскопии тонких
металлических фольг.
28
29.
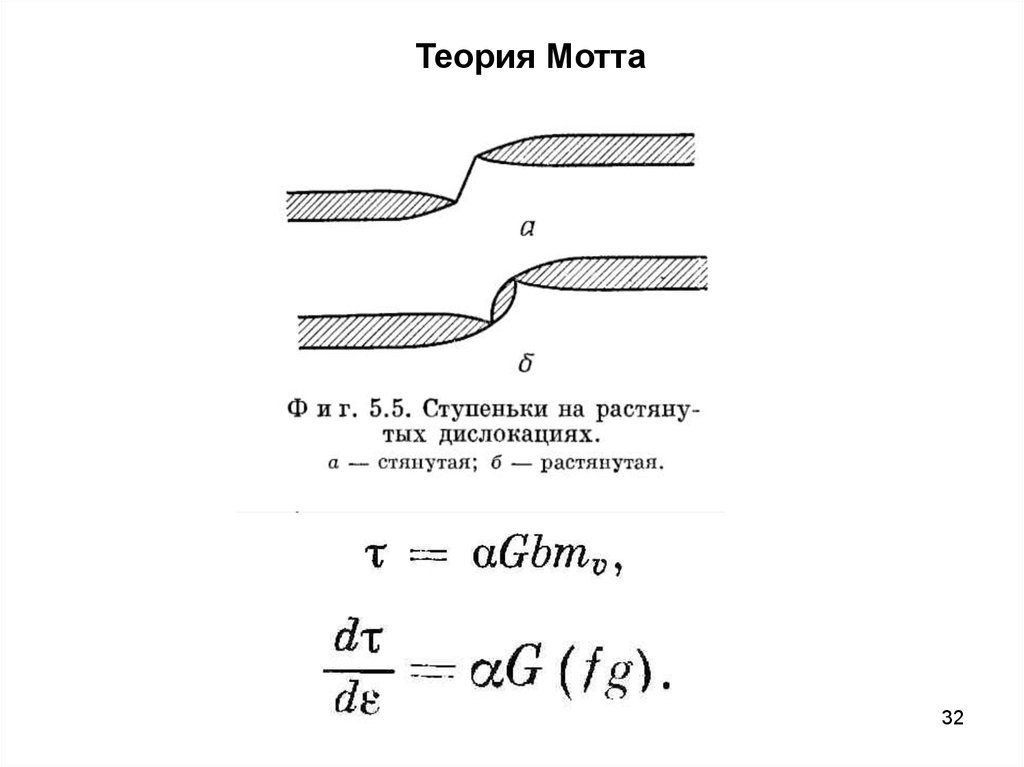
Мотт и Хирш развили теорию, в которой предполагается, чтосопротивление течению обусловлено сидячими ступеньками
на дислокациях.
Показано, что ступеньки на дислокациях появляются при их
пересечении. Во многих случаях ступеньки способны
двигаться вместе с остальной частью дислокации (ступеньки
образовались на краевой дислокации), но для винтовых
дислокаций неконсервативное движение ступенек вместе с
дислокационной линией должно быть энергетически
невыгодным, так как при этом порождаются вакансии или
междоузельные атомы. Считается, что ступеньки склонны
диссоциировать на частичные дислокации, разделенные
дефектами упаковки,
29
30.
Если подобные ступеньки тянутся за движущимисядислокациями, то образуются диполи. С другой стороны,
если напряжение и (или) температура достаточно высоки,
то ступеньки могут стягиваться и оказываются способными
скользить вдоль оси винтовых дислокаций консервативным
образом.
Ступеньки, которые должны порождать междоузельные
атомы, если их вынудить двигаться неконсервативно, могут
скользить консервативно вдоль дислокации в том случае,
когда они стянуты. С другой стороны, ступеньки,
приводящие к образованию вакансий, не стягиваются под
действием приложенных напряжений и поэтому являются
более трудными препятствиями, если температура
недостаточно высока для того, чтобы вакансии могли легко
диффундировать от ступенек.
30
31.
Мотт положил, что дислокационные источники на первичныхплоскостях скольжения содержат ступеньки благодаря
влиянию дислокаций, находящихся на вторичных системах, и
что для разблокировки дислокационного источника со
ступеньками
необходимо
напряжение
течения
определяемое выражением
Gbm
v
31
32.
Теория Мотта32
33.
Возвращаясь теперь к скольжению по вторичным плоскостям,примем, что оно происходит в g раз чаще, чем по первичной
плоскости; тогда если m — число ступенек на единицу длины, то
мы имеем
dm = g R2dN
(5/27)
33
34.
Но из числа ступенек dm лишь малая частьпредставляет собой вакансионные ступеньки, т. е.
dmv
dmv = fdm
Тогда из соотношений (5.25) и (5.27) получаем
Используя выражение (5.26), запишем
d
G fg
d
34
35.
Эта теория успешно объясняет ряд важных характерныхчерт второй стадии упрочнения гранецентрированных
кубических
металлов.
Упрочнение
обусловлено
увеличением плотности ступенек на первичных источниках
скольжения, и после разблокировки этих источников
образуются линии скольжения. Ступеньки могут быть
термически активируемыми, что объясняет меньшие
напряжения течения при повышенных температурах. Теория
согласуется также с экспериментом в том отношении, что
краевые дислокации движутся на большие расстояния, чем
винтовые, на поведении которых больше сказывается
образование вакансионных ступенек.
35
36.
С другой стороны, теория требует протекания вторичногоскольжения в довольно значительном масштабе (g 1/3);
кроме того, теоретическая длина пути скольжения меньше,
чем наблюдаемая. Далее, на практике коэффициент
упрочнения на второй стадии в зависимости от
ориентировки кристалла изменяется сравнительно слабо,
хотя склонность к протеканию вторичного скольжения при
этом существенно различна, что по теории должно
приводить к заметным изменениям величины II.
36
37.
Хиршем сделана попытка развить общую теорию второйстадии упрочнения, в
которой основное внимание
уделено
рассмотрению
наблюдаемых
длин
пути
скольжения и того факта, что при исследовании в
электронном микроскопе тонких фольг в них наблюдаются
сгущения
дислокаций.
Они
являются
главным
препятствием для дальнейшего скольжения. Затем
действуют
новые
источники,
и
дислокации,
скапливающиеся около препятствий, также релаксируют и
пополняют наблюдаемые сгущения. Таким образом,
количество препятствий прямо связано с числом
источников
37
38.
3839.
3940.
Несмотря на значительное число теоретических иэкспериментальных работ, посвященных изучению второй
стадии упрочнения, общей приемлемой теории этой стадии
пока нет и появление ее в ближайшем будущем
маловероятно.
40
41.
Третья стадия упрочненияГлавными
особенностями
этой
стадии
являются
уменьшение скорости упрочнения (по параболическому
закону) и тенденция к снижению напряжения её с
повышением температуры. Согласно общепринятой точке
зрения, барьеры, возникшие на второй стадии упрочнения,
на третьей стадии разрушаются. Если считать приемлемой
общую картину образования барьеров Ломер — Коттрела
на второй стадии, то третья стадия наступает тогда, когда
влияние барьеров преодолевается одним из следующих
двух способов:
а) разрушение барьеров путем рекомбинации частичных
дислокаций, составляющих сидячую дислокацию Ломер
Коттрелла (имеется несколько возможных механизмов
такого процесса);
б) обход барьеров путем поперечного скольжения по
плоскостям, имеющим общее направление сдвига41 с
первичной плоскостью скольжения.
42.
Наступление третьей стадии характеризуется появлениемгрубых полос скольжения с частым поперечным
скольжением. Степень развития этого явления зависит от
величины энергии дефекта упаковки данного металла.
Металлы с относительно малой энергией дефекта упаковки
для поперечного скольжения требуют высокой энергии
активации, так как прежде, чем может произойти локальный
акт поперечного скольжения, широкий дефект упаковки
между частичными дислокациями должен сжаться, образуя
отрезок нерастянутой дислокации. Так, для получения
заметной скорости поперечного скольжения в меди при
комнатной температуре необходимо приложить очень
высокое напряжение
42
43.
.Сдругой стороны, в металле с большой энергией дефекта
упаковки, таком, как алюминий, при комнатной температуре
деформации третья стадия упрочнения появляется очень
рано, поскольку дислокации не растянуты, вследствие чего
поперечное скольжение может
происходить при
значительно меньшем приложенном напряжении. Важно
отметить, что на третьей стадии длина линий скольжения
не увеличивается, как можно было бы ожидать в случае
разрушения барьеров Ломер Коттрела.
43
44.
Предложено следующее выражение для напряжения сдвига, необходимого для слияния частичных дислокаций в
лидирующей дислокации скопления:
где энергия дефекта упаковки, n число дислокаций в
скоплении.
Напряжение соответствует напряжению III начала
третьей стадии при температуре, достаточно низкой для
того,
чтобы
исключить
термическую
активацию.
Используя значения III для свинца и алюминия при 4 К
44
получаем n 25.





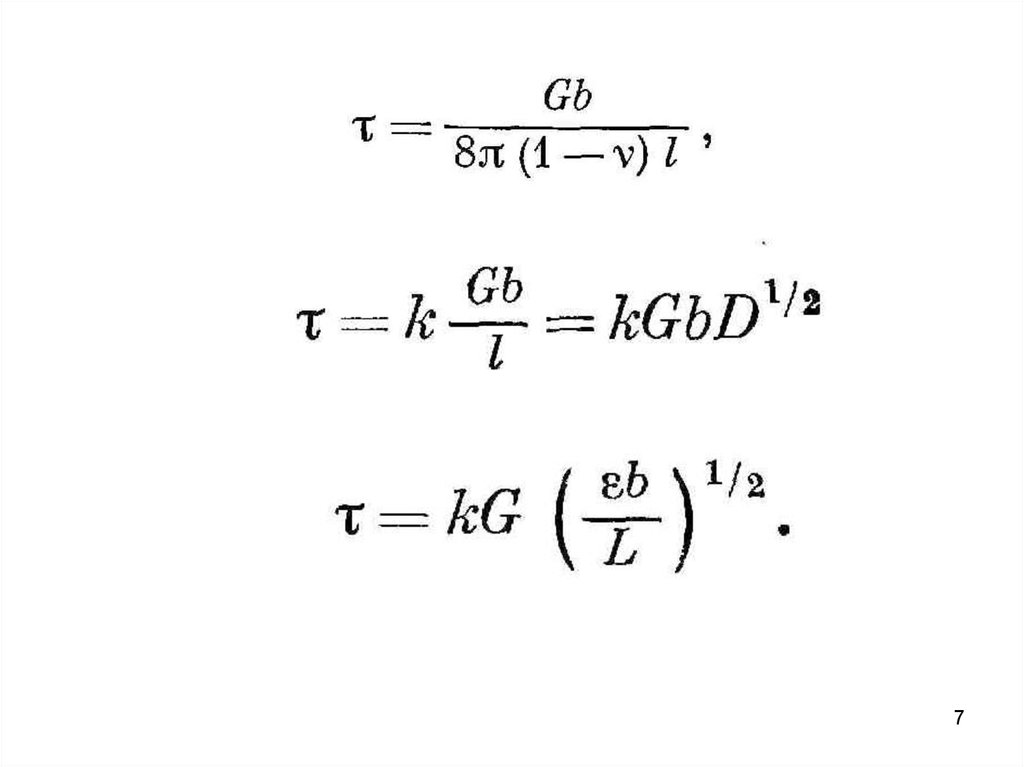







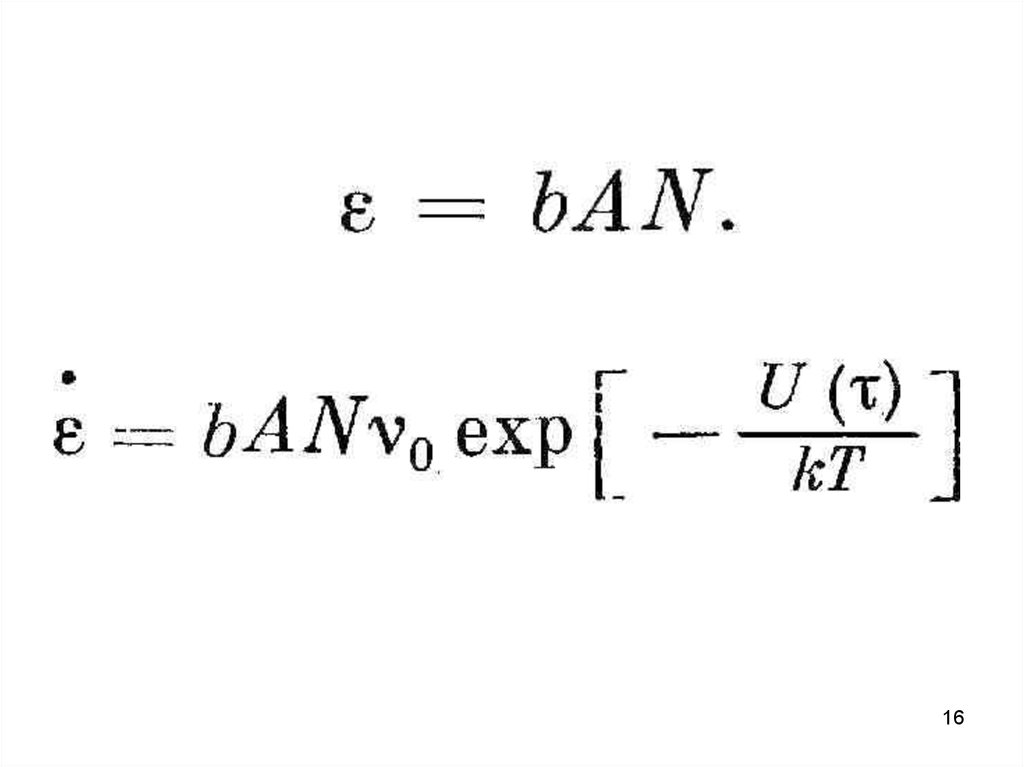
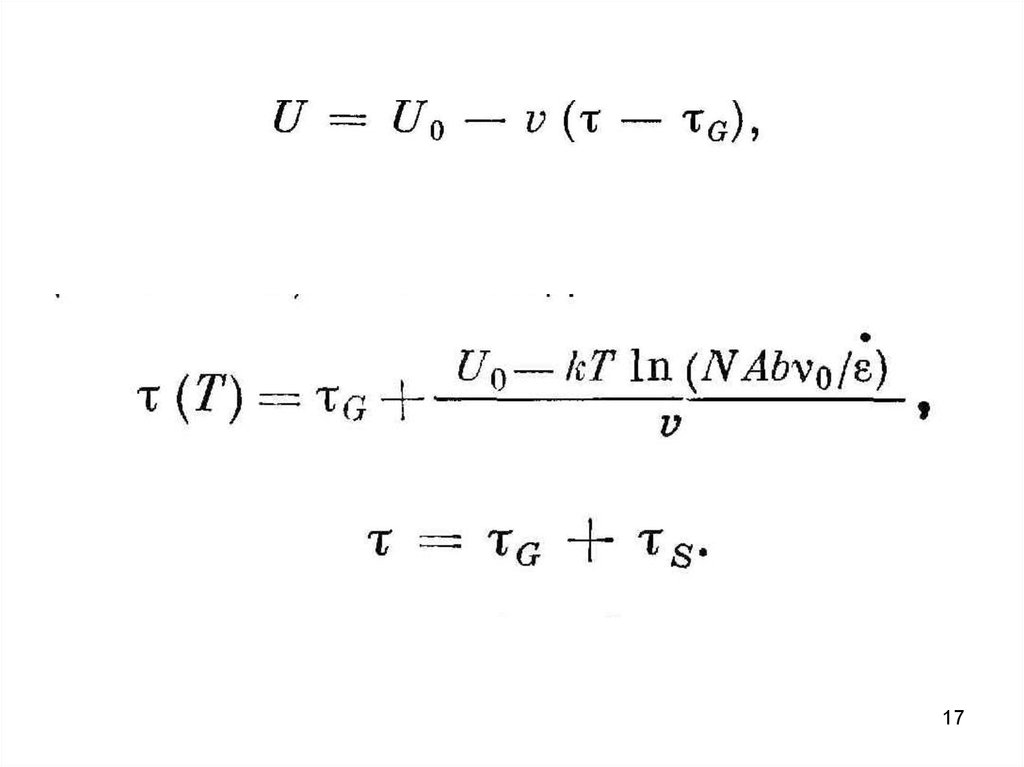



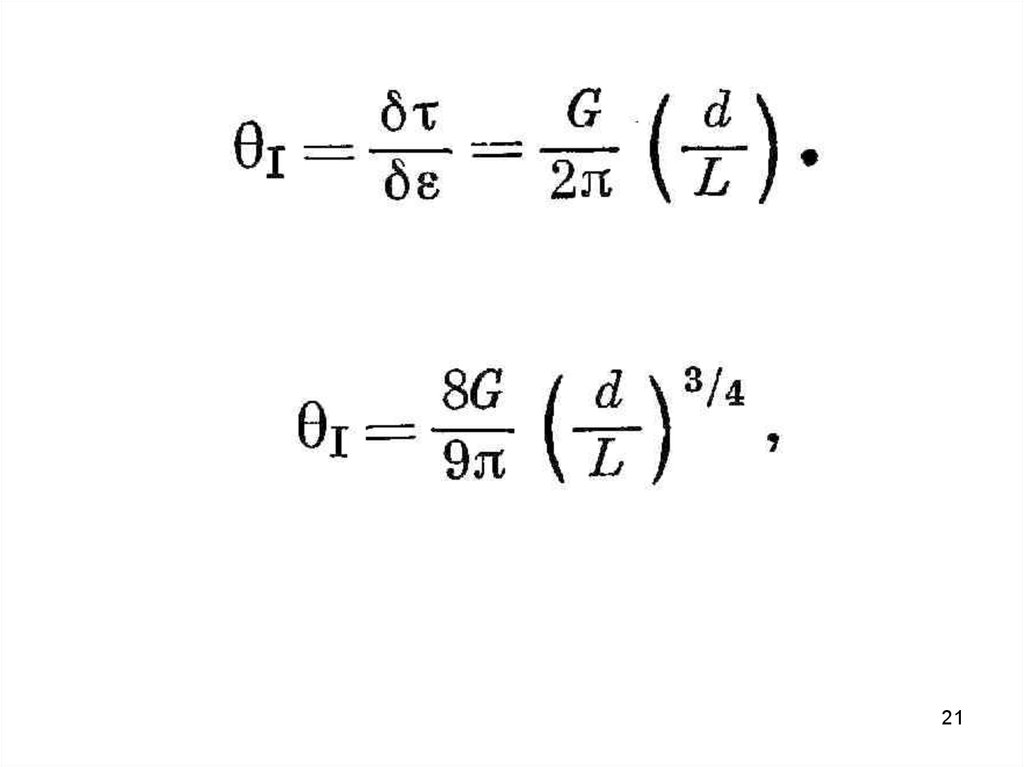




















 physics
physics








