Similar presentations:
Жидкости. Строение и свойства жидкостей
1.
2. Жидкости2.1. строение и свойства жидкостей. Энергия
поверхностного слоя. Поверхностное натяжение
Жидкость
является
агрегатным
состоянием вещества, промежуточным между
газообразным и твердым.
В
жидкостях
имеет
место
называемый
ближний
порядок
расположении частиц.
так
в
Каждая молекула в течение некоторого
промежутка времени колеблется около
определенного положения равновесия.
1
2.
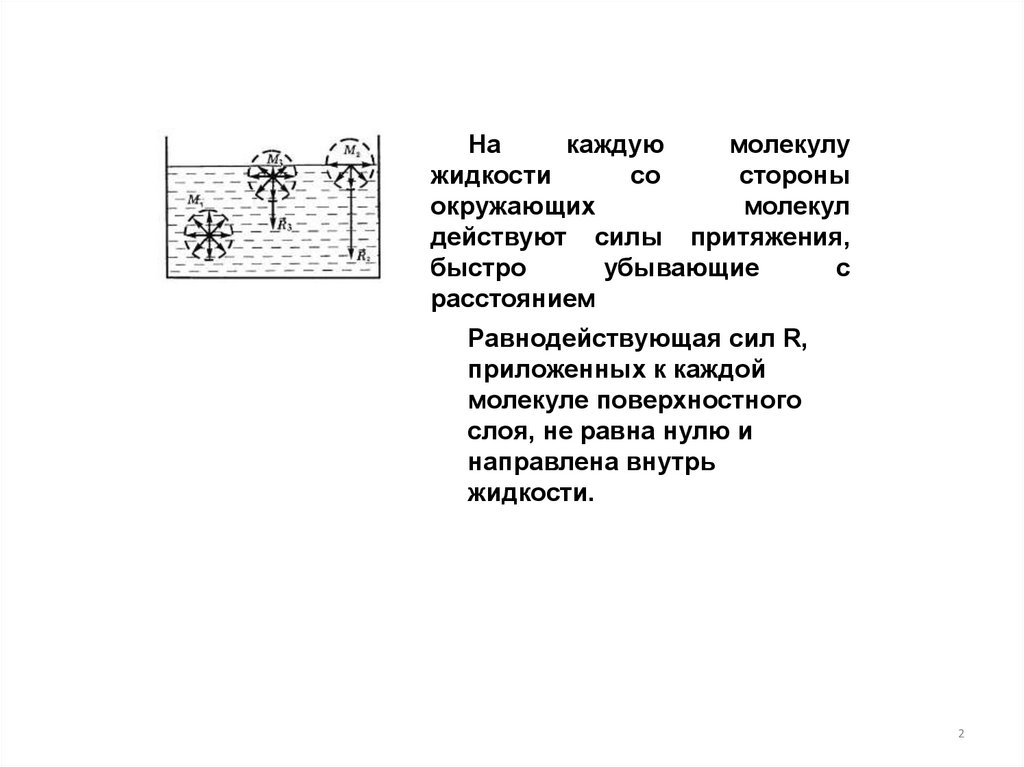
Накаждую
молекулу
жидкости
со
стороны
окружающих
молекул
действуют силы притяжения,
быстро
убывающие
с
расстоянием
Равнодействующая сил R,
приложенных к каждой
молекуле поверхностного
слоя, не равна нулю и
направлена внутрь
жидкости.
2
3.
Молекулы жидкости, находящиеся в еёповерхностном слое, втягиваются внутрь жидкости,
их потенциальная энергия больше, чем у молекул
внутри жидкости.
Эту дополнительную потенциальную энергию молекул
поверхностного слоя жидкости называют свободной
энергией или поверхностной.
Она пропорциональна площади слоя S:
E S ,
— поверхностное натяжение.
Равновесное состояние характеризуется минимумом
потенциальной энергии.
Поверхность жидкости стремится сократиться.
3
4.
Рассмотрим поверхность жидкости,ограниченную замкнутым контуром.
Под действием сил поверхностного
натяжения поверхность жидкости
сократилась и рассматриваемый
контур переместился в новое
положение.
Силы, действующие со стороны
выделенного участка на граничащие
с ним участки, совершают работу
A f l x ,
f — сила поверхностного натяжения, действующая на единицу
длины контура поверхности жидкости.
4
5.
Поверхностная сила, приходящаяся на единицудлины
контура,
называется
коэффициентом
поверхностного натяжения:
Единица поверхностного натяжения — (Н/м) .
5
6.
2.2. Давление под искривленной поверхностьюжидкости
Сферическая выпуклая поверхность производит на
жидкость дополнительное давление, определяемое силами
натяжения:
6
7.
2p
,
R
R – радиус сферы.
В общем случае избыточное давление для
произвольной поверхности определяется
формулой Лапласа:
1
1
p
,
R1 R2
R1 и R2 — радиусы
кривизны двух любых
взаимно перпендикулярных
нормальных сечений
поверхности жидкости.
7
8.
2.3. Явление на границе жидкости и твердого тела. Смачивание.Смачивание
–
явление,
возникающее
при
соприкосновении жидкости с поверхностью твёрдого
тела или другой жидкости.
В первом случае говорят, что жидкость смачивает твердую
поверхность, во втором — не смачивает ее.
В смачивающей жидкости силы притяжения между молекулами
жидкости и твердого тела больше, чем между молекулами самой
жидкости.
Для несмачивающей жидкости силы притяжения между
молекулами жидкости и твердого тела меньше, чем между молекулами
жидкости.
8
9.
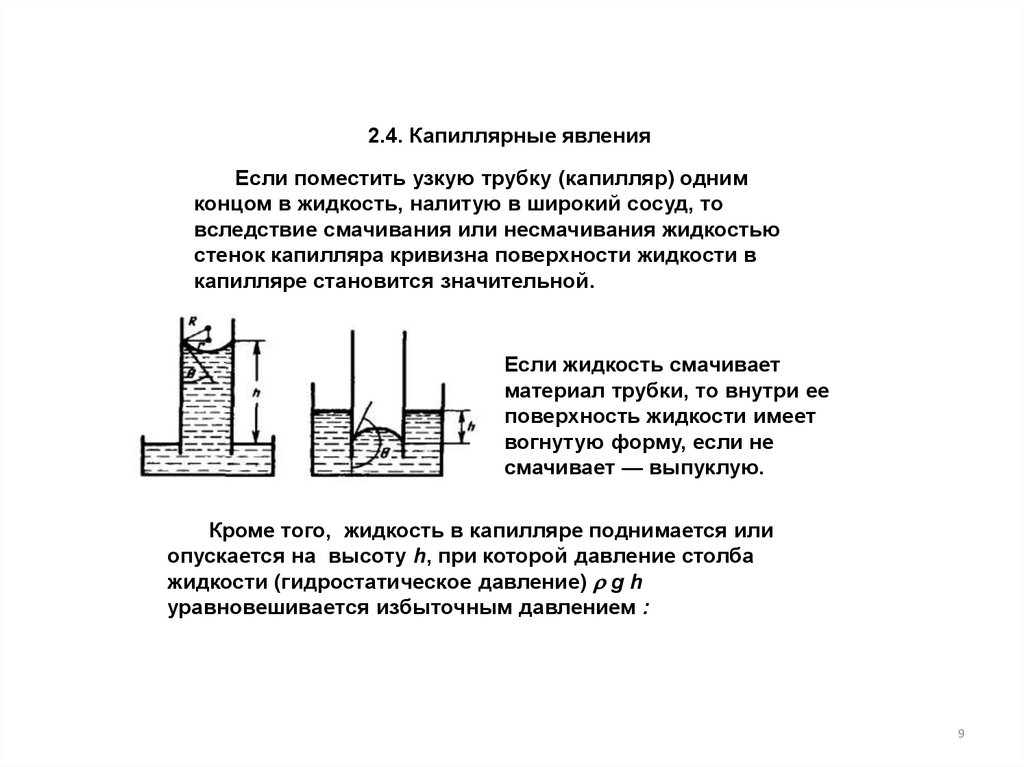
2.4. Капиллярные явленияЕсли поместить узкую трубку (капилляр) одним
концом в жидкость, налитую в широкий сосуд, то
вследствие смачивания или несмачивания жидкостью
стенок капилляра кривизна поверхности жидкости в
капилляре становится значительной.
Если жидкость смачивает
материал трубки, то внутри ее
поверхность жидкости имеет
вогнутую форму, если не
смачивает — выпуклую.
Кроме того, жидкость в капилляре поднимается или
опускается на высоту h, при которой давление столба
жидкости (гидростатическое давление) g h
уравновешивается избыточным давлением :
9
10.
Определение высоты столба жидкости.2
g h,
R
— плотность жидкости,
g — ускорение свободного падения.
Если r — радиус капилляра, — краевой угол, то:
2 cos
g h,
r
2 cos
h
.
gr
В тонких капиллярах жидкость поднимается достаточно
высоко. При полном смачивании вода ( =1000 кг/м3, = 0,073 Н/м)
в капилляре диаметром 10 мкм поднимается на высоту h 3 м.
10








 physics
physics








