Вращающиеся тросовые космические системы

1.

ВРАЩАЮЩИЕСЯ
ТРОСОВЫЕ
КОСМИЧЕСКИЕ
СИСТЕМЫ
Видеоролики о работе:
https://youtu.be/jm8u2EgKOGA
https://youtu.be/DZI0r_NWbsk
https://youtu.be/YNtzB8CiioY
Екимовская Анна Алексеевна,
ученица 10 класса, дружный кружок «Юный физик –
умелые руки», Благотворительный фонд «Образование+»
при МБОУ «Гимназия №5» города Королёва (Юбилейный)
Московской области, МАОУ «Средняя
общеобразовательная школа №40» города Череповца
Вологодской области, 8-996-513-61-49,
[email protected]
Научный руководитель Лебедев Владимир Валентинович,
доктор технических наук,
Центр физико-математического образования Московского авиационного института (НИУ),
Заслуженный деятель науки и техники Московской области,
руководитель школьного кружка «Юный физик – умелые руки»,
Тел. 8-903184-45-31, 8-925-717-14-37, [email protected], личный сайт CFMO.UCOZ.RU
Работа проводится при поддержке Благотворительного фонда «Образование+»

2.

Анализ литературы и направление исследований

3.

Идея – одна школьная задача статики
Это исследовательская
задача

4.

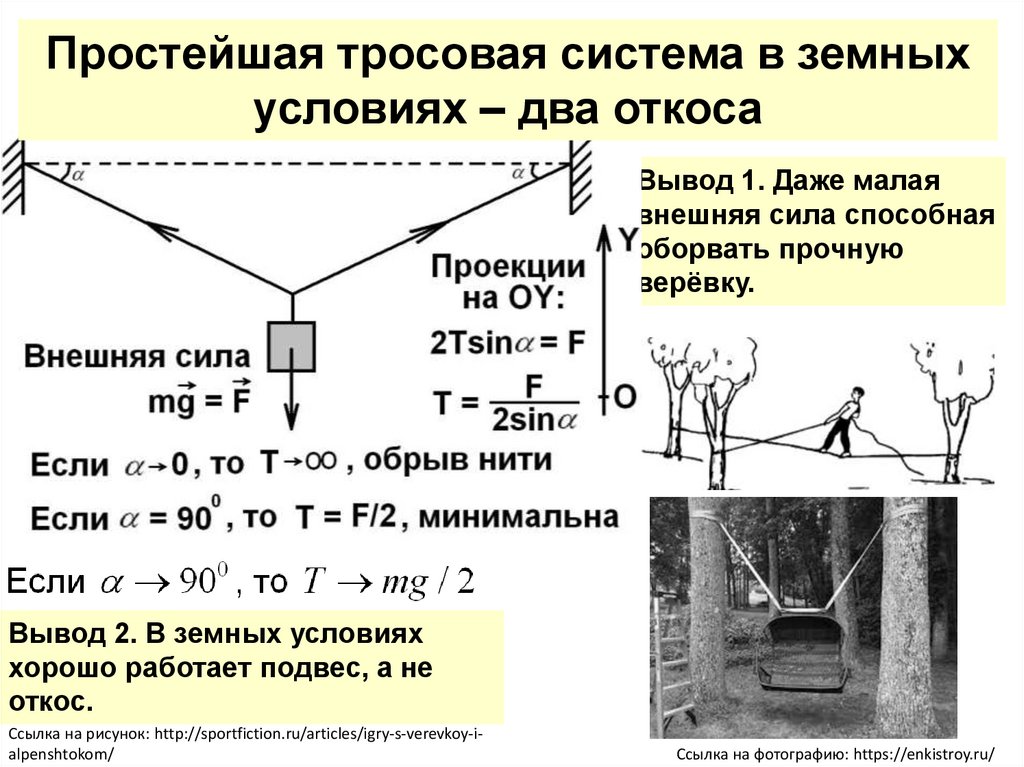
Простейшая тросовая система в земных
условиях – два откоса
Вывод 1. Даже малая
внешняя сила способная
оборвать прочную
верёвку.
Вывод 2. В земных условиях
хорошо работает подвес, а не
откос.
Ссылка на рисунок: http://sportfiction.ru/articles/igry-s-verevkoy-ialpenshtokom/
Ссылка на фотографию: https://enkistroy.ru/

5.

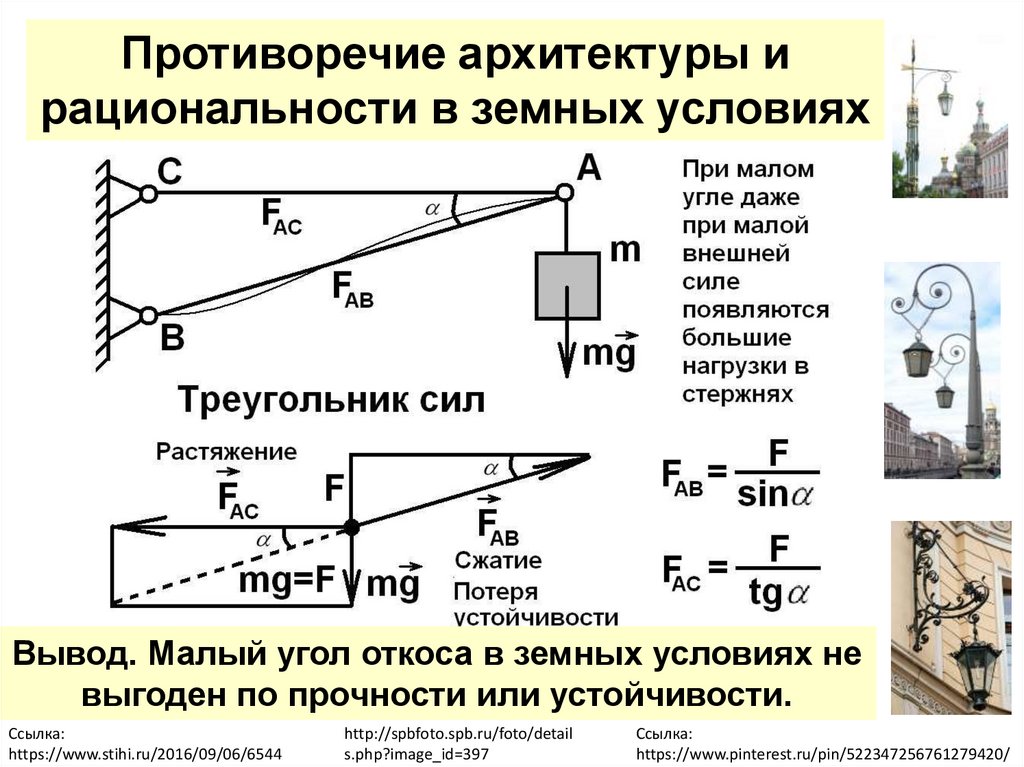
Противоречие архитектуры и
рациональности в земных условиях
Вывод. Малый угол откоса в земных условиях не
выгоден по прочности или устойчивости.
Ссылка:
https://www.stihi.ru/2016/09/06/6544
http://spbfoto.spb.ru/foto/detail
s.php?image_id=397
Ссылка:
https://www.pinterest.ru/pin/522347256761279420/

6.

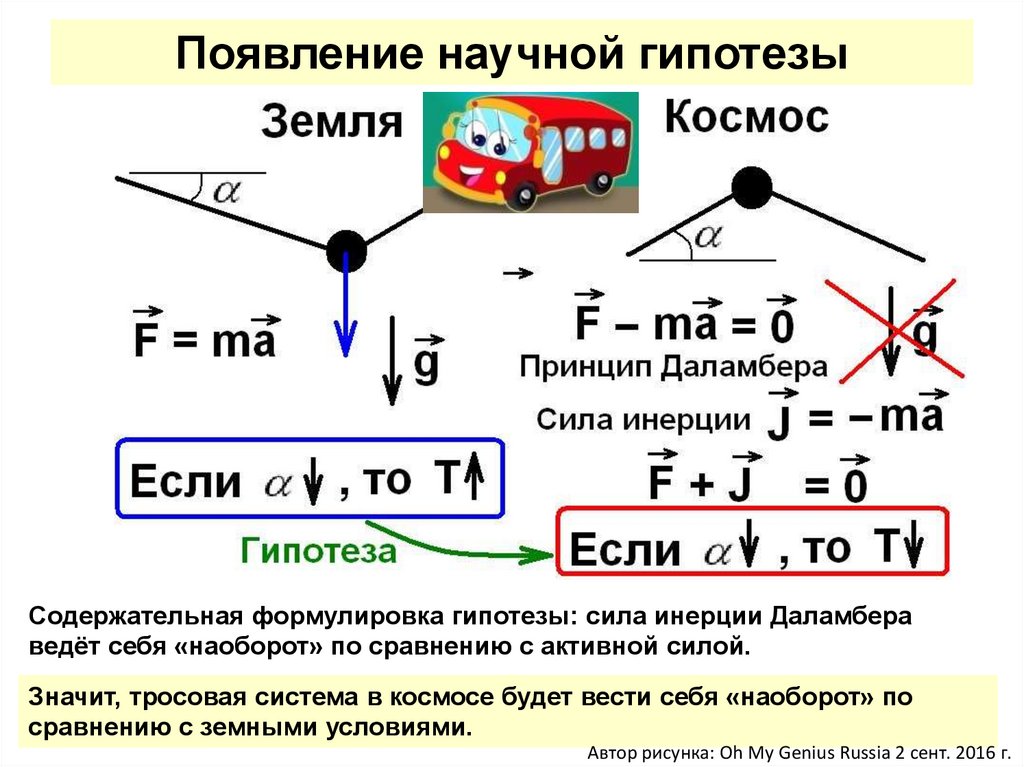
Появление научной гипотезы
Содержательная формулировка гипотезы: сила инерции Даламбера
ведёт себя «наоборот» по сравнению с активной силой.
Значит, тросовая система в космосе будет вести себя «наоборот» по
сравнению с земными условиями.
Автор рисунка: Oh My Genius Russia 2 сент. 2016 г.

7.

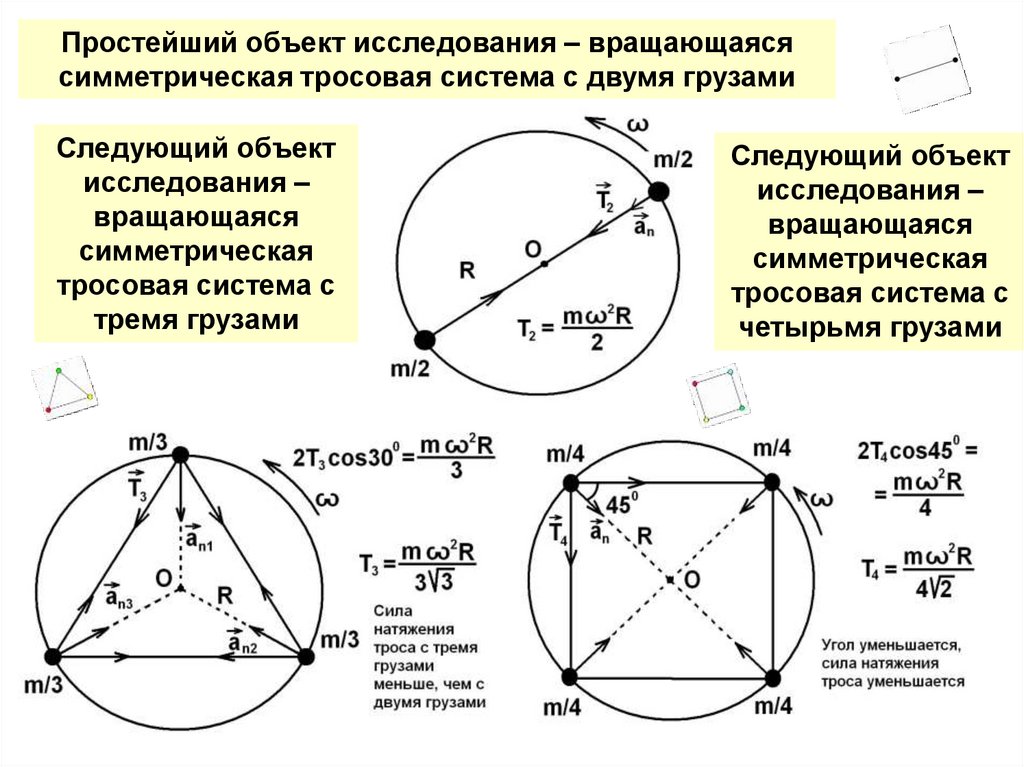
Простейший объект исследования – вращающаяся
симметрическая тросовая система с двумя грузами
Следующий объект
исследования –
вращающаяся
симметрическая
тросовая система с
тремя грузами
Следующий объект
исследования –
вращающаяся
симметрическая
тросовая система с
четырьмя грузами

8.

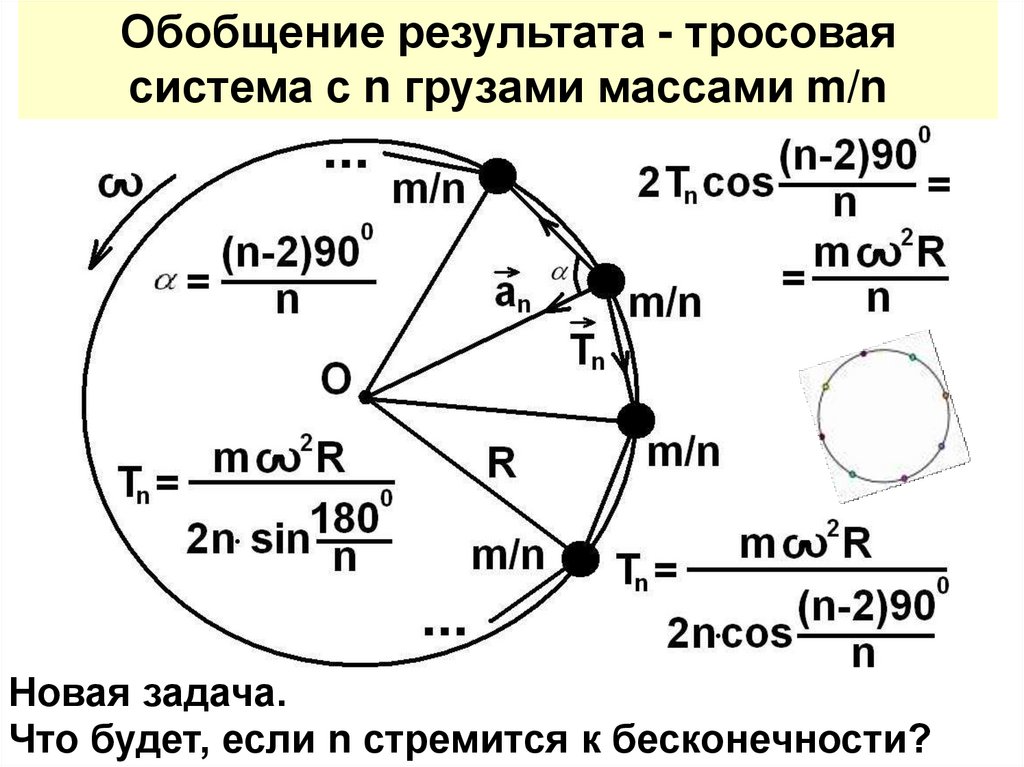
Обобщение результата - тросовая
система с n грузами массами m/n
Новая задача.
Что будет, если n стремится к бесконечности?

9.

Первый способ решения
(математический)
Теоретическая основа
Результат решения
задачи – предельного
перехода (асимптотики)

10.

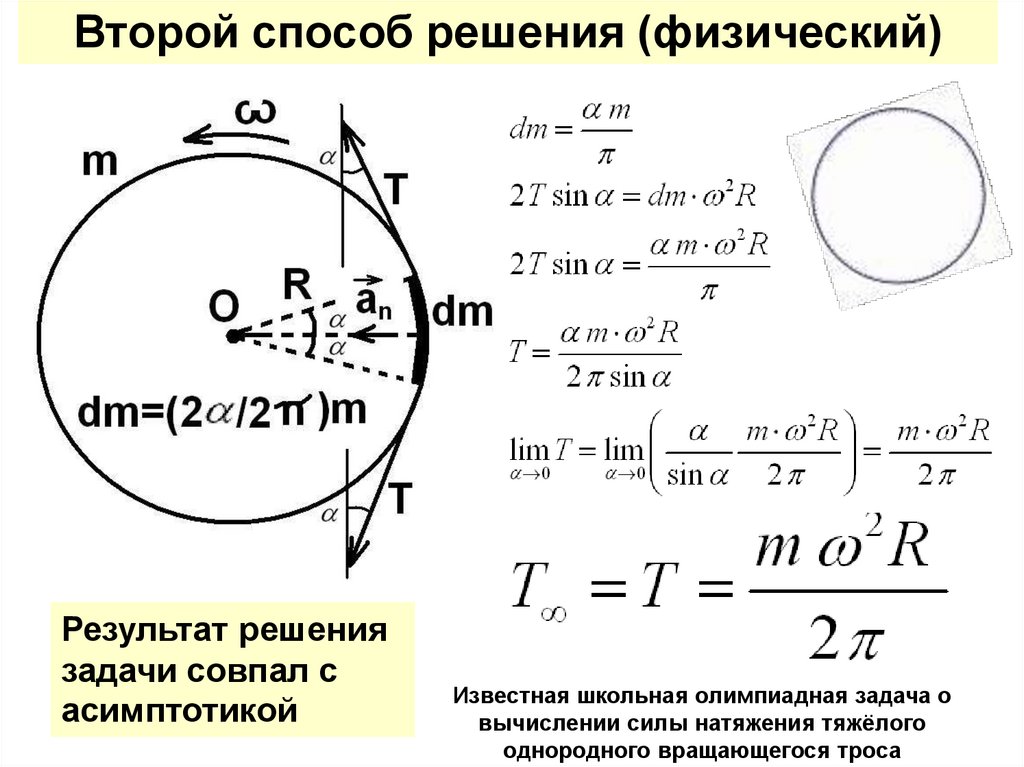
Второй способ решения (физический)
Результат решения
задачи совпал с
асимптотикой
Известная школьная олимпиадная задача о
вычислении силы натяжения тяжёлого
однородного вращающегося троса

11.

Основное различие в нагрузке
1) На Земле при уменьшении угла откоса нагрузка возрастает
2) В космосе при уменьшении угла откоса нагрузка уменьшается
Распределённые массы уменьшают нагрузку более чем в три раза

12.

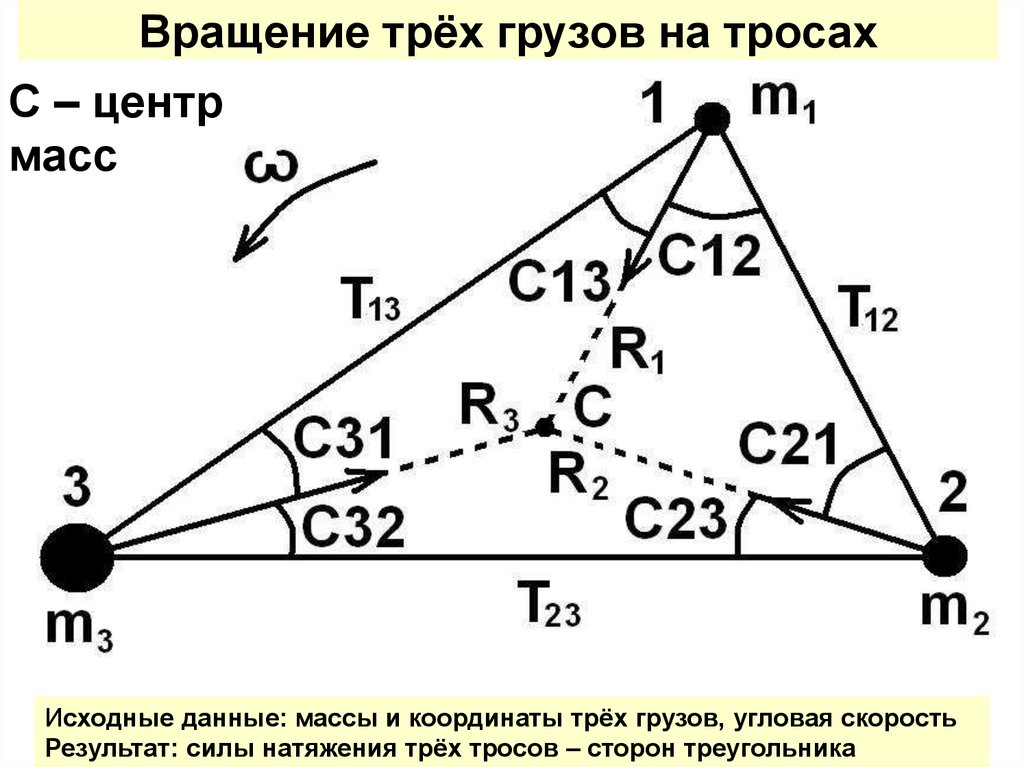
Вращение трёх грузов на тросах
С – центр
масс
Исходные данные: массы и координаты трёх грузов, угловая скорость
Результат: силы натяжения трёх тросов – сторон треугольника

13.

Методика решения задачи
Исходные данные: массы и координаты трёх грузов, угловая скорость
Результат: силы натяжения трёх тросов – сторон треугольника
1) Определить положение центра масс системы:
2) Определить радиусы вращения:
3) Определить центростремительные ускорения:

14.

4) Определить шесть углов при вершинах треугольника:
методы векторной алгебры, скалярное произведение векторов, длина вектора.
Проверка: сумма шести углов равна 180 градусов – сумма углов треугольника.

15.

5) Составить систему уравнений для определения сил:
6) Решить систему уравнений, определить три силы
1) Метод Гаусса (самый «мощный»)
2) Метод Крамера («хорошие» системы)
3) Метод обращения матрицы (в школе не изучают)
Метод Крамера
В физических задачах удаётся предсказать
существование и единственность решения
(корректность задачи по А.Н.Тихонову)

16.

Решение системы линейных уравнений методом Крамера
Результат решения

17.

Программа расчёта натяжения трёх тросов
треугольной системы (Excel)
Исходные данные: массы и координаты трёх грузов, угловая скорость
Результат: силы натяжения трёх тросов – сторон треугольника

18.

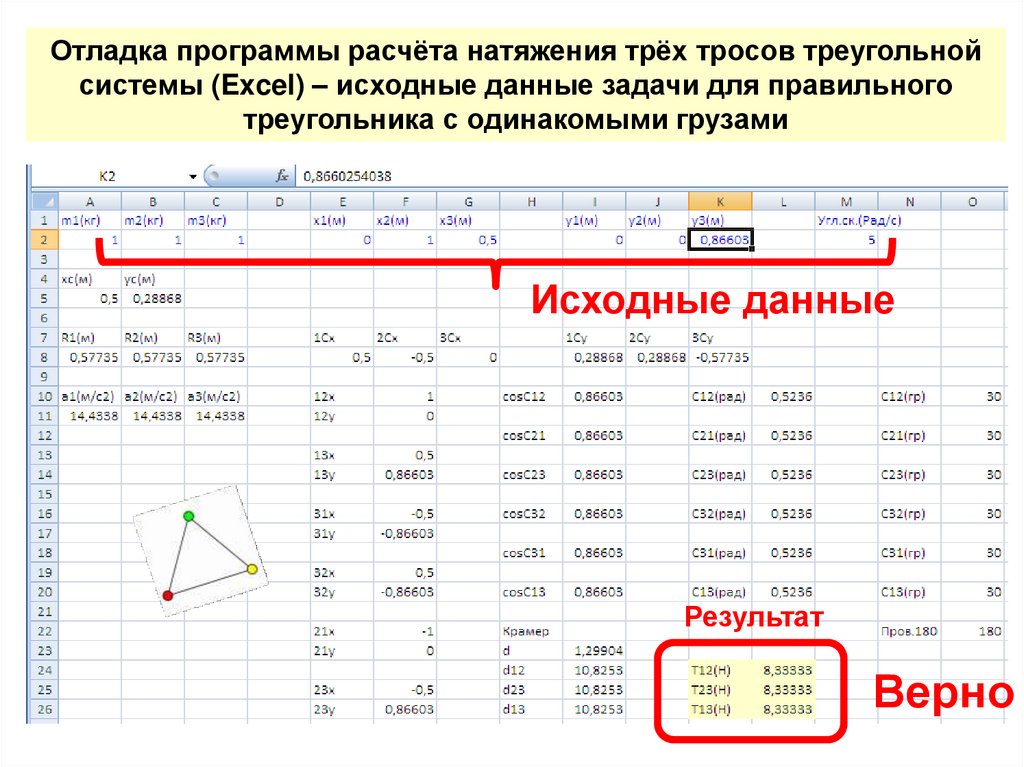
Отладка программы расчёта натяжения трёх тросов треугольной
системы (Excel) – исходные данные задачи для правильного
треугольника с одинакомыми грузами
Исходные данные
Результат
Верно

19.

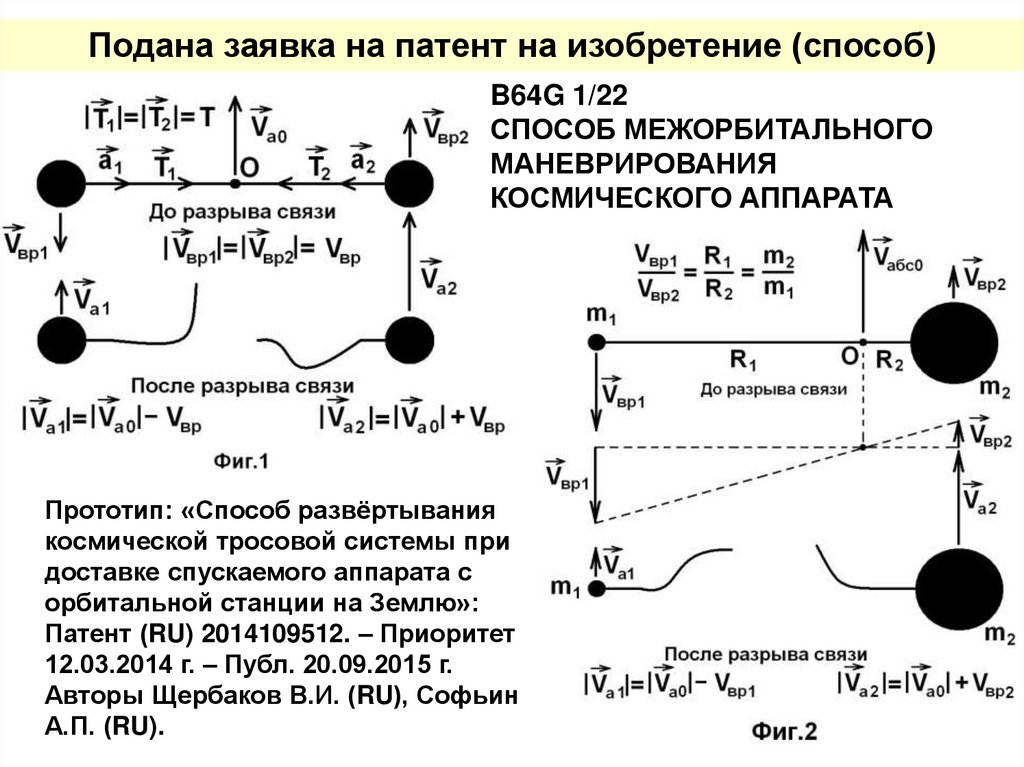
Подана заявка на патент на изобретение (способ)
B64G 1/22
СПОСОБ МЕЖОРБИТАЛЬНОГО
МАНЕВРИРОВАНИЯ
КОСМИЧЕСКОГО АППАРАТА
Прототип: «Способ развёртывания
космической тросовой системы при
доставке спускаемого аппарата с
орбитальной станции на Землю»:
Патент (RU) 2014109512. – Приоритет
12.03.2014 г. – Публ. 20.09.2015 г.
Авторы Щербаков В.И. (RU), Софьин
А.П. (RU).

20.

Выводы
Методологический вывод
Доказано, что космические вращающиеся тросовые системы с позиции
нагрузки конструкции ведут себя противоположно земным условиям.
Методические выводы
1. Решена задача о силе натяжения тросов в произвольной
вращающейся космической системе.
2. Предложен метод математического предельного перехода для
изучения вращения непрерывно распределённой массы троса.
3. Новизна! Впервые решена задача о силе натяжения тросов в
произвольной треугольной космической системе.
Практические выводы
1. Предложена рабочая программа для расчёта силы натяжения тросов
в произвольной треугольной космической системе.
2. Подана заявка на патент на изобретение «Способ межорбитального
маневрирования космического аппарата» с применением тросовой
системы.
Определён перспективный план изучения космических тросовых систем