Similar presentations:
Линейное программирование. Двойственные задачи
1.
Задания на Лабораторную Работу (практическое занятие) 1.Двойственные задачи ЛП.
Графический способ решения.
Двойственные задачи ЛП.
Признак оптимальности в краткой форме.
2.
Графический метод решения задачи ЛП.Основные этапы графического метода решения
1. Построить прямые, уравнения которых получаются в результате замены
в ограничениях (5) знаков неравенства на знаки равенства.
2. Найти полуплоскости заданные неравенствами.
3. Найти область допустимых решений (ОДР).
4. Построить вектор n = { c1, c2} нормальный к прямым μ(x)=с1 х1 + с2 х2 .
5. Построить линию уровня h=с1 х1 + с2 х2 проходящую через ОДР.
6. Передвинуть линию уровня в направлении вектора n , в результате найти точку
или установить неограниченность функции сверху или снизу.
7. Определить координаты точки, т.е. Оптимальное решение.
Филиппова А.С., каф. ИТ, БГПУ
2
3.
1. Решить графически задачу линейного программирования:а) Максимизировать:
μ(х1, х2) = 2х1 + 3х2
х = (х1, х2)
х1 ≥ 0, х2 ≥ 0,
4х1 – 3х2 ≤ 4,
1.6 х1 + х2 ≤ 2,
2.5 х1 + 5х2 ≤ 5
б) Минимизировать:
μ(х1, х2) = – х1 – х2
х = (х1, х2)
х1 ≥ 0, х2 ≥ 0,
3х1 – 4х2 ≤ 6,
х1 + 2х2 ≤ 8,
– 6 х1 + 8х2 ≤ 5
в) Максимизировать:
μ(х1, х2) = 7х1 + х2
х = (х1, х2)
х1 ≥ 0, х2 ≥ 0,
х1 + х2 – 1 ≥ 0,
3х1 – х2 – 1 ≥ 0,
7х1 - 3х2 – 1 ≥ 0,
– х1 + 3х2 – 1 ≥ 0,
4.
Основная задача ЛП:Филиппова А.С., каф. ИТ, БГПУ
4
5.
Двойственная задача ЛП:Филиппова А.С., каф. ИТ, БГПУ
5
6.
2. Записать двойственную задачуа) Максимизировать:
μ(х) = 2х1 + х2 – х3 + х4
х = (х1, х2, х3, х4, х5 )
х2 ≥ 0, х4 ≥ 0, х5 ≥ 0,
3х1 + 2х2 – 3х4 + х5 + 20 ≥ 0,
2х1 + х3 + х4 – 6х5 + 30 = 0,
х1 + х2 + х3 + х4 + х5 + 15 = 0,
7.
б)в)
г)
8.
Следствие 1Достаточный признак оптимальности в краткой
форме. Для оптимальности допустимого вектора (2) в
задаче I достаточно, чтобы в задаче I* нашелся допустимый
вектор (7), удовлетворяющий условию
μ(x) = ν(y)
при этом допустимый вектор (7) является оптимальным в
задаче I*.
Филиппова А.С., каф. ИТ, БГПУ
8
9.
3. Записать двойственную задачу и используя признак оптимальности (вкраткой форме) найти оптимальные вектора x и y
Максимизировать:
μ(х) = – 3х1 – 8х2
х = (х1, х2)
х2 ≥ 0,
х1 + 2х2 + 1 = 0,






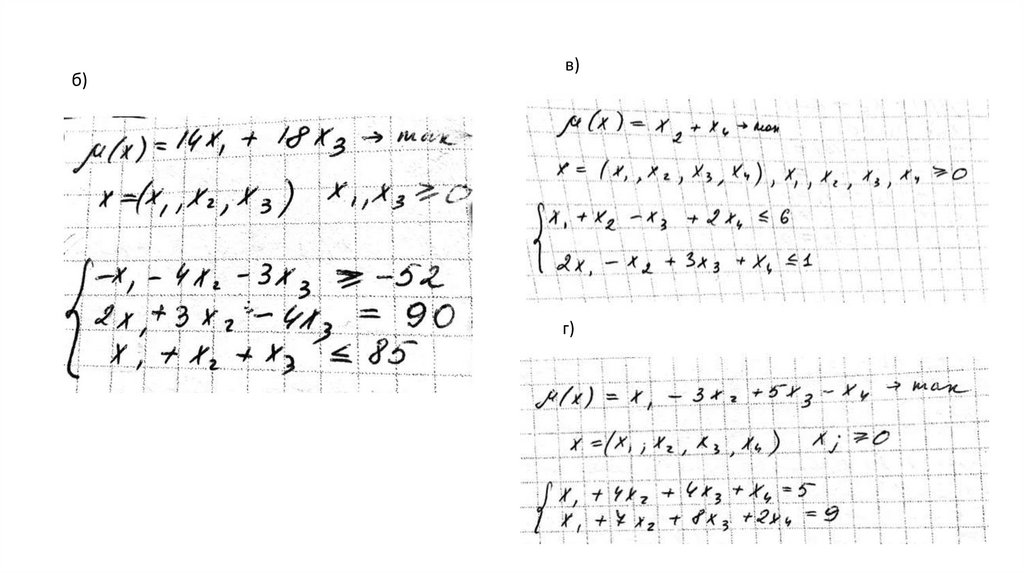


 mathematics
mathematics








