Методика изучения трехмерных геометрических фигур. Тела вращения: цилиндр, конус, шар, сфера

1.

Методика изучения трехмерных
геометрических фигур. Тела
вращения: цилиндр, конус, шар,
сфера.
Выполнил:
студентка группы ЗНОЛу-117
Коробова О.В.
Владимир, 2020

2.

Цель начального математического
образования
формирование геометрических представлений об образах геометрических
фигур, их элементов, отношений между фигурами и их элементами;
выработка практических умений и навыков в измерениях и построении
простейших геометрических фигур с помощью чертежных инструментов;
развитие
пространственных
представлений,
воображения
и
пространственного мышления учащихся;
обогащение математического словарного запаса, развитие речи учащихся.

3.

«Геометрия для младших школьников»
под редакцией В.А. Панчинщиной
от трехмерного пространства к двухмерному;
от
наглядных
изображений
схематическим и обратно;
от одной системы отсчета к другой.
к
условно-

4.

Программы для изучения темы
«Тела вращения»
3D Studio MAX позволяет представить тела вращения в пространстве,
рассмотреть подробно их сечение.
Microsoft PowerPoint программа для создания и проведения
презентаций, помогает наглядно представлять тела вращения.
Google SketchUp 7 программа для моделирования относительно
простых трёхмерных объектов, позволяет построить тела вращения,
сечение тел вращения.

5.

Схема изучения геометрических фигур
получение фигуры;
название фигуры ;
распознавание фигуры в окружающей
обстановке;
построение фигуры;
изучение свойств.

6.

Программой распределения
геометрических понятий по классам:
1 класс - Точка. Линия. Прямая и кривая линии. Отрезок.
2 класс - Углы. Прямой угол.
Прямоугольник. Квадрат. Периметр прямоугольника и квадрата. Ломаная.
Звенья
ломаной. Длина ломаной.
3 класс - Луч. Треугольник. Равносторонний треугольник. Прямоугольный
треугольник. Тупоугольный треугольник. Остроугольный треугольник.
4 класс - Представление о телах: куб, призма, пирамида, конус, цилиндр,
шар, сфера.

7.

Тела вращения —
объемные тела,
образующиеся
из-за вращения
плоской фигуры,
ограниченной
кривой, вокруг
оси.

8.

Тела вращения— объёмные тела,
возникающие при вращении
замкнутой линии вокруг оси,
лежащей в той же плоскости, что и
вращающееся тело.

9.

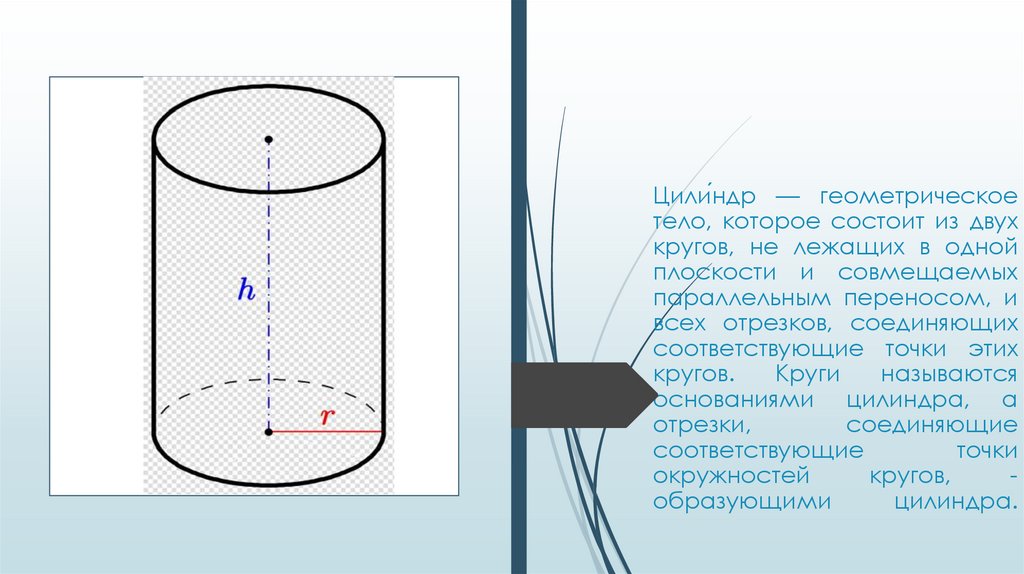
Цили́ндр — геометрическое
тело, которое состоит из двух
кругов, не лежащих в одной
плоскости и совмещаемых
параллельным переносом, и
всех отрезков, соединяющих
соответствующие точки этих
кругов.
Круги
называются
основаниями цилиндра, а
отрезки,
соединяющие
соответствующие
точки
окружностей
кругов,
образующими
цилиндра.

10.

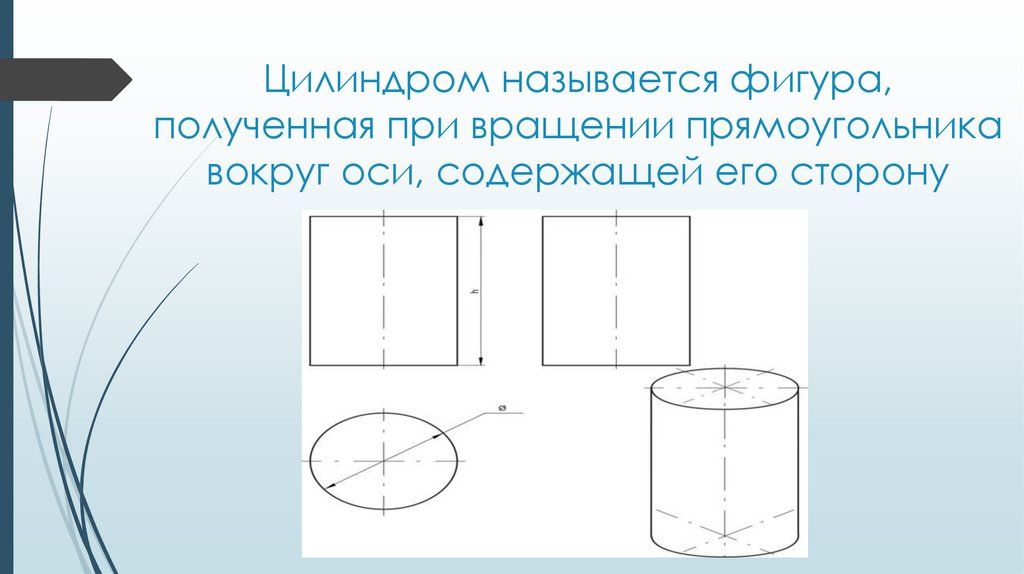
Цилиндром называется фигура,
полученная при вращении прямоугольника
вокруг оси, содержащей его сторону

11.

Тела, имеющие форму цилиндра

12.

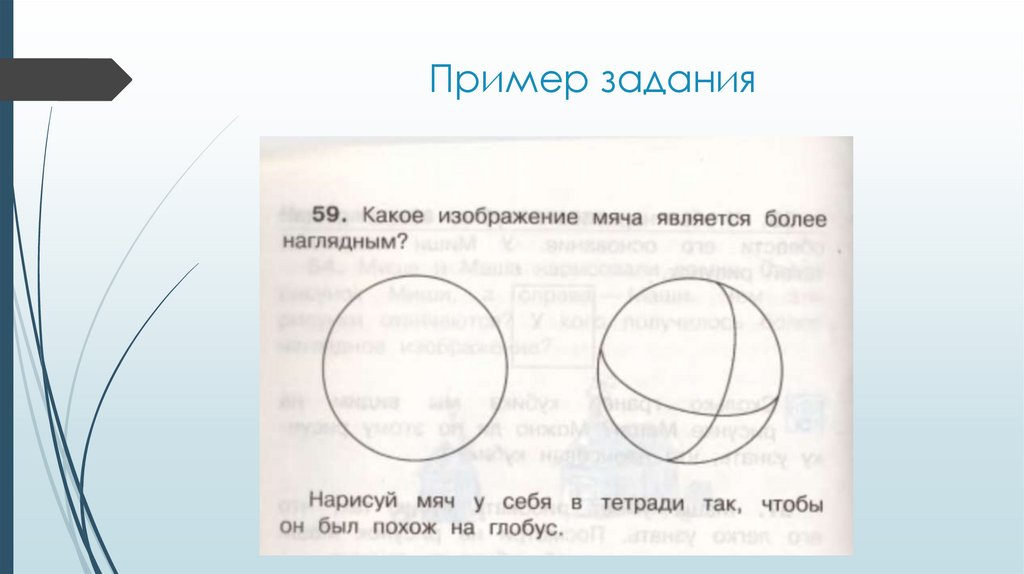
Пример задания

13.

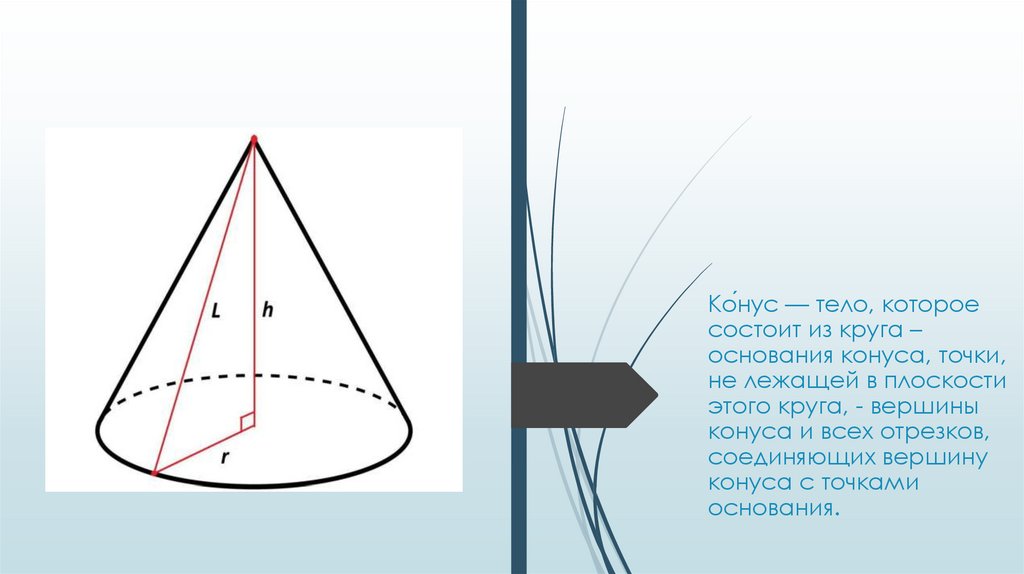
Ко́нус — тело, которое
состоит из круга –
основания конуса, точки,
не лежащей в плоскости
этого круга, - вершины
конуса и всех отрезков,
соединяющих вершину
конуса с точками
основания.

14.

Развертка конуса
Конус — это тело, ограниченное кругом и
конической поверхностью.

15.

Свойства конуса

16.

Пример задания

17.

Шар — геометрическое тело, ограниченное
поверхностью, все точки которой отстоят на
равном расстоянии от центра.
Поверхность шара называется сферой.

18.

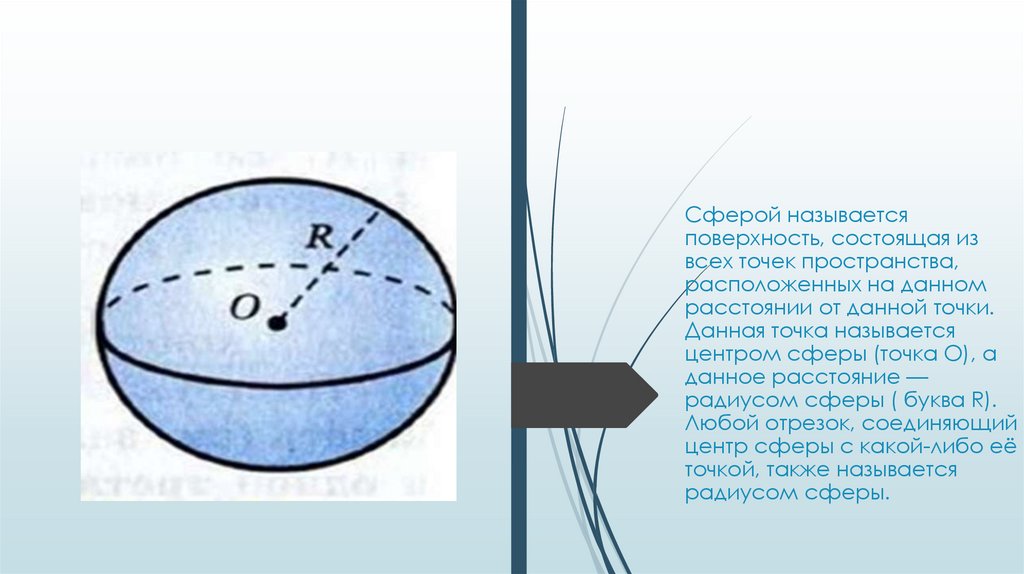
Сферой называется
поверхность, состоящая из
всех точек пространства,
расположенных на данном
расстоянии от данной точки.
Данная точка называется
центром сферы (точка О), а
данное расстояние —
радиусом сферы ( буква R).
Любой отрезок, соединяющий
центр сферы с какой-либо её
точкой, также называется
радиусом сферы.

19.

Пример задания

20.

Пример задания

21.

Основными задачами изучения трехмерных
геометрических фигур в 1-4 классах являются:
1)
формирование
пространственных
представлений
и
развитие
воображения, умений наблюдать, сравнивать, абстрагировать и обобщать;
2) выработка у учащихся практических навыков измерения и
построения
геометрических
фигур
с
помощью
измерительных
и
чертежных инструментов;
3) формирование умений использовать наглядность в приобретении
знаний.

22.

Программа по матиматике М.И.Моро,
Ю.М.Колягиной, М.А.Бантовой и др

23.

Программа по математике А. Л. Чекина,
Р.Г. Чураковой

24.

Программа по математике Л.В. Занкова

25.

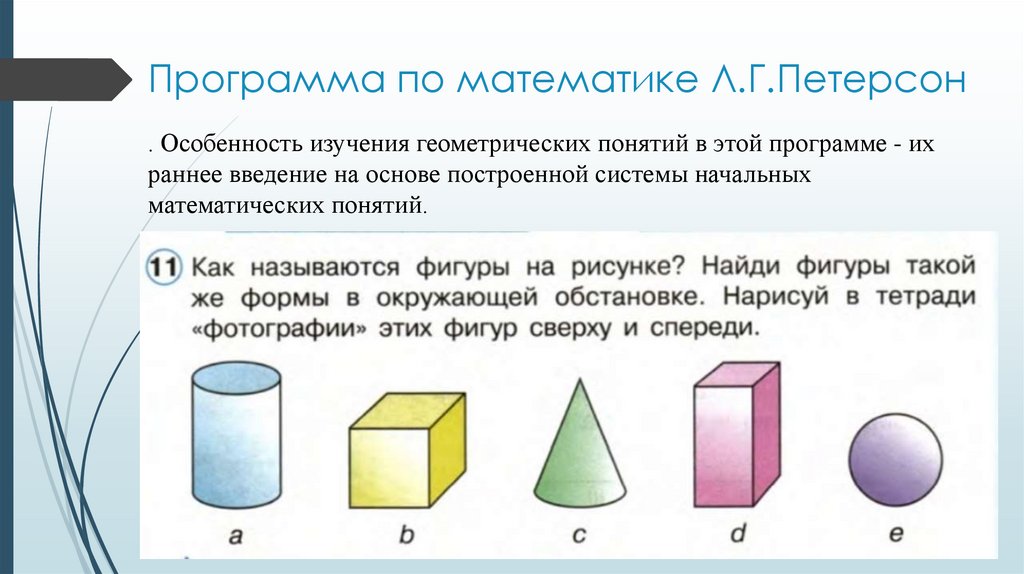
Программа по математике Л.Г.Петерсон
. Особенность изучения геометрических понятий в этой программе - их
раннее введение на основе построенной системы начальных
математических понятий.

26.

Программа по математике Л.Г.Петерсон
Сравнительно рано появляются в курсе простейшие
пространственные образы: куб, параллелепипед, шар, цилиндр,
пирамида, конус.

27.

Программа по математике Л.Г.Петерсон
Выявление различных геометрических закономерностей, которые
формируют, как предложение, гипотезу, которые затем необходимо
логически обосновать, доказать.

28.

Программа по математике Н.Б. Истомина
При изучении геометрического материала учащиеся учатся группировать,
находить лишнюю фигуру из предложенных.

29.

Программа по математике Н.Б. Истомина

30.

Программа по математике Н.Б. Истомина
Изучение признаков и свойств трехмерных геометрических тел

31.

Условия эффективности изучения
трехмерных геометрических фигур в
начальной школе
1. Имеющийся опыт детей, уточнение и обогащение их представлений.
2 Наглядный и практический методический подход.
3. Применение разнообразных наглядных пособий.
4. Практические работы учащихся, их наблюдения и работы с геометрическими объектами.
6. Применению приема сопоставления и противопоставления геометрических фигур.
6. Систематическая работа с применяемыми символами и чертежами.
7. Набор чертежно-измерительных инструментов для выполнения чертежей на доске.
8. Общее представление о системе задач, представленных в учебниках и максимально
эффективно использовать ее возможности.