Similar presentations:
Уравнение неразрывности. Уравнение Рапорта-Лиса. Модель Бакли-Леверта
1.
Уравнение неразрывности.Уравнение Рапорта-Лиса.
Модель Бакли-Леверта.
2.
Уравнение неразрывности.• Для начала рассмотрим однофазный поток сквозь элемент
пористой средыИз соображения материального баланса можно
записать, что, вычитая из входящей массы (MACCAвх) массу
выходящую (MACCAвых), получим накопленную (или
потерянную) в рассматриваемом объеме массу:
MACCAвх − MACCAвых = MACCA∆ .
• Изменение массы флюида, содержащегося в выделенном
где
элементарном
объёме за время dt, запишем в следующем виде:
∂
dM = (mρdv )dt
∂t
3.
• Где m -пористость;• ρ- плотность.
• Изменение массы в выделенном элементарном объёме
может происходить за счёт двух составляющих:
• -dM - перетоки жидкости через элементарную поверхность
dΩ :
- dM 2 - наличие источников и стоков в этом элементарном объёме:
dM
2
= (ρ Q нагн − ρ Q доб )dt
Тогда можно записать:
dM = dM 1 + dM
2
Подставляя выражения для dM , dM 1 и dM 2 , получим:
r r
∂
m ⋅ ρ ⋅ dVdt = − (ρ ⋅ v ⋅ n )d Ω dt + (ρ Q нагн − ρ Q доб )dt
∂t
4.
Пусть отсутствуют источники и стоки, тогда:rr
∂
(
m
ρ
dV
ρ
v
+
∫Ω n )dΩ = 0
∂t V∫
(6.7)
В соответствии с теоремой Остроградского-Гаусса можно перейти от
поверхностного интеграла к объёмному:
r r
r
(
)
(
)dV
ρ
⋅
v
⋅
n
d
Ω
=
div
ρ
⋅
v
∫
∫
Ω
(6.8)
V
,
где
r dv dv dv
div(v ) =
+
+ .
dx dy dz
Тогда, подставляя полученное в (5.1) под знак интеграла, получим:
r
∂mρ
(
) dV = 0
+
div
ρ
v
∫V ∂t
.
(6.9)
5.
Для любого «физического» объёма следует, что данное равенство выполняетсятогда, когда подынтегральное выражение равно нулю:
r
∂mρ
+ div(ρv ) = 0
∂t
(6.10)
Это уравнение задаёт закон сохранения массы в пористой среде в
дифференциальной форме или уравнение неразрывности.
Для одномерного случая уравнение запишется так:
∂mρ ∂ρv
+
=0
∂t
∂x
(6.11)
6.
Уравнение РаппопортаЛиса.Будем считать, что жидкости и пористая среда несжимаемы (
ρ i = const , m = const ). Тогда, проведя ряд математических преобразований,
получим уравнение неразрывности для водной фазы, известное также как
уравнение Раппопорта-Лиса:
m
∂s ∂s ∂s k ⋅ k н
∂P
+ +
F (s ) ⋅ c − g∆ρsinα = 0
∂t ∂x ∂x µ н
∂x
(6.12)
где
v = v н + vв ,
F (s ) =
- функция Бакли-Леверетта.
k в (s )
µ
k в (s ) + в k н (s )
µн
(6.13)
7.
• Физический смысл функции Бакли-Леверетта – этосоответствие её доле воды в двухфазном потоке жидкости
в пористой среде. На этой основе далее в курсе будет
рассмотрено моделирование процесса вытеснения нефти
водной, так называемая «модель двухфазной фильтрации
Бакли-Леверетта».
• Это уравнение представляет собой нелинейное уравнение
параболического типа второго порядка. Точные решения
этих уравнений получены лишь для некоторых
сравнительно простых случаев. Это уравнение в
трехмерном случае является основой гидродинамического
моделирования с применением численных методов
решения и используется всеми основными пакетами
программ для построения геолого-технологических
моделей пласта.
8.
Методика расчета распределения водонасыщенностив линейном однородном пласте по модели
фронтального вытеснения
(модель Бакли-Леверетта)
•Она разработана для непоршневого вытеснения нефти водой
с учетом различия вязкости и относительных фазовых
проницаемостей нефти и воды. Согласно модели
непоршневого вытеснения в пласте образуются три зоны:
•Полностью заводненная зона, где насыщенность водой достигла
своего максимального значения и не меняется;
•Обширная зона совместного движения нефти и воды, где
насыщенность водой в направлении вытеснения меняется от
максимального значения Sm до связанной водонасыщенности
Sсв;
•Незаводненная зона, где в пористой среде содержится
неподвижная связанная вода и подвижная нефть с
насыщенностью, равной начальной нефтенасыщенности.
Рассмотрим процесс вытеснения нефти водой из однородного
линейного пласта при заданном расходе закачиваемой воды V.
Жидкости несжимаемые, порода недеформируемая. Длина пласта L,
поперечное сечение пласта для простоты пусть в*h=l.
9.
• Движение нефти и воды подчиняются закону Дарси:(14)
(15)
sв + s н = 1
и уравнению неразрывности:
s = 1 − sн
(16)
(17)
(18)
Сложив уравнения (17) и (18), можно убедиться, что в любом
поперечном сечении пласта расход жидкости остается
постоянным:
(19)
10.
• Сложив (14) и (15), с учетом (19) найдем:(20)
• Подставляя в (14), получим:
(21)
• где
(22)
• Полученное выражение называется функцией Бакли-Леверетта,
показывающей долю воды в потоке жидкости. Из (14) определим:
(23)
и подставим в (17). Получим:
или
(24)
11.
• Уравнение (23) есть квазилинейное дифференциальноеуравнение первого порядка в частных производных.
• Найдем полный дифференциал от S = s(x,t).
(25)
Рассмотрим на плоскости (x,t) такие линии х (t), вдоль которых
насыщенность воды постоянна:
На этой линии ds=0, поэтому уравнение (24) принимает вид:
(26)
Рассмотрим систему уравнений (23) и (25) относительно S'X И s't.
Правая часть ее равна нулю. Из курса высшей математики
известно, что она имеет решение только тогда, когда
определитель этой системы равен нулю:
12.
Отсюда получим:(26)
С учетом s = const, из (26) имеем:
(27)
где хо - значение координаты с начальной насыщенностью So при t= 0.
•Для фиксированного t пo (27) можно рассчитывать координаты х для
любого заданного значения насыщенности.
•Проанализируем полученное решение (27), для чего
продифференцируем (27) пo t:
(28)
•Из выражения (28) видно, что правая часть ее показывает скорость
распространения насыщенности s вдоль координаты х.
13.
•График зависимости f'(s) при SCB=0,1, Sm=0.9 имеет вид,показанный на рис.1. Из графика видно, что f'(s) немонотонная функция, т.е. имеет два значения S1 и S2,
имеющие одинаковую скорость распространения. Поэтому
распределение насыщенности может оказаться
многозначным.
Такое
распределение
физически не
возможно.
Неоднозначность
распределения
насыщенности
устраняется
введением скачка
насыщенности или
фронтовой
насыщенности.
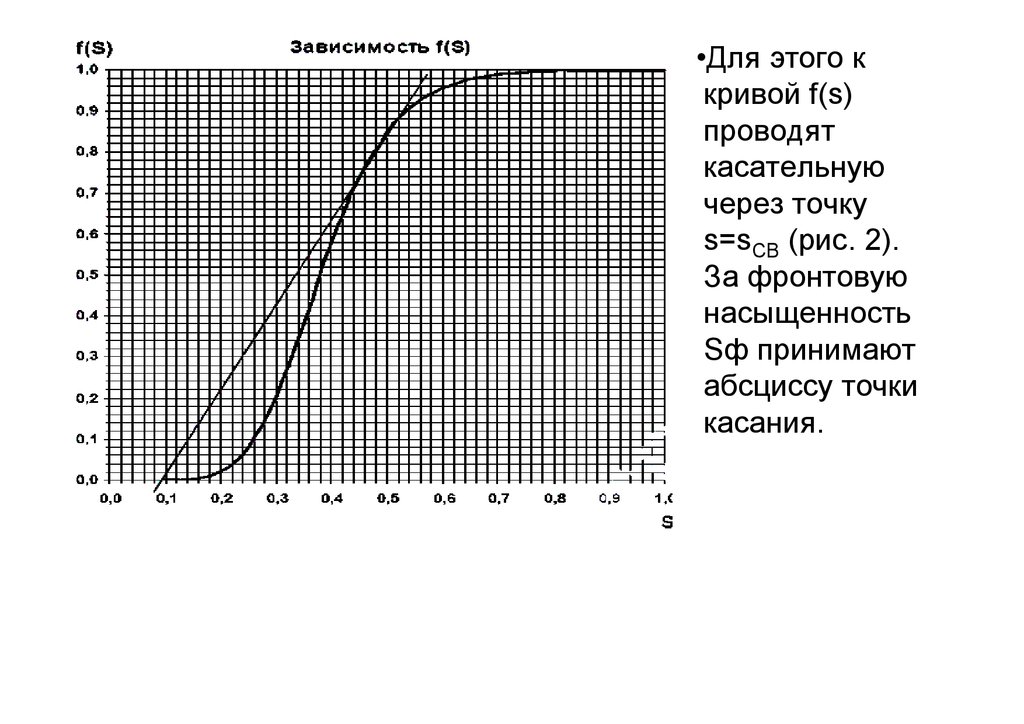
Рисунок 1 -Зависимость f(S)
14.
•Для этого ккривой f(s)
проводят
касательную
через точку
s=sCB (рис. 2).
За фронтовую
насыщенность
Sф принимают
абсциссу точки
касания.
15.
• Далее по уравнению (27), задавая значениянасыщенности из интервала sф ≤ s ≤ smax , для каждого
момента времени строят график зависимости S от х (рис.
3).
16.
Методика расчета технологических показателейразработки
по модели непоршневого вытеснения нефти водой
по схеме Бакли-Леверетта
• Полученное выше решение позволяет выполнить расчеты всех
технологических показателей разработки пласта, которые
проводятся в следующей последовательности. Ниже приводится
последовательность расчетов.
1. Фронтовая насыщенность Sф определяется графически, но более
точно из уравнения:
(1)
где
(2)
μо=μн/μв.
17.
2. Распределение водонасыщенности по длине пласта определяется поуравнению
(3)
для всех S≥ Sф .
3. Время прорыва воды определяется по соотношению
(4)
4. Накопленные отборы до прорыва воды:
нефти
(5)
∑ QН = 0
воды
(6)
5. Водонасыщенность на выходе после прорыва воды определяется по
уравнению:
(7)
18.
6. Обводнённость добываемой нефти7. Средняя водонасыщенность в заводненной зоне:
• в безводный период добычи нефти:
(9)
• после прорыва воды:
(10)
8. Коэффициент нефтеизвлечения:
(11)
19.
9. Накопленная добыча нефти и воды после прорыва водыопределяются по формулам:
(12)
10. Годовая добыча нефти и воды определяются как разность между
накопленным значением за текущий и предыдущий годы


















 industry
industry








