Similar presentations:
Физико-математические аспекты нефтегазового дела
1. Физико-математические аспекты нефтегазового дела
Основы подземной гидродинамики.Многофазные потоки флюидов в
пористых средах
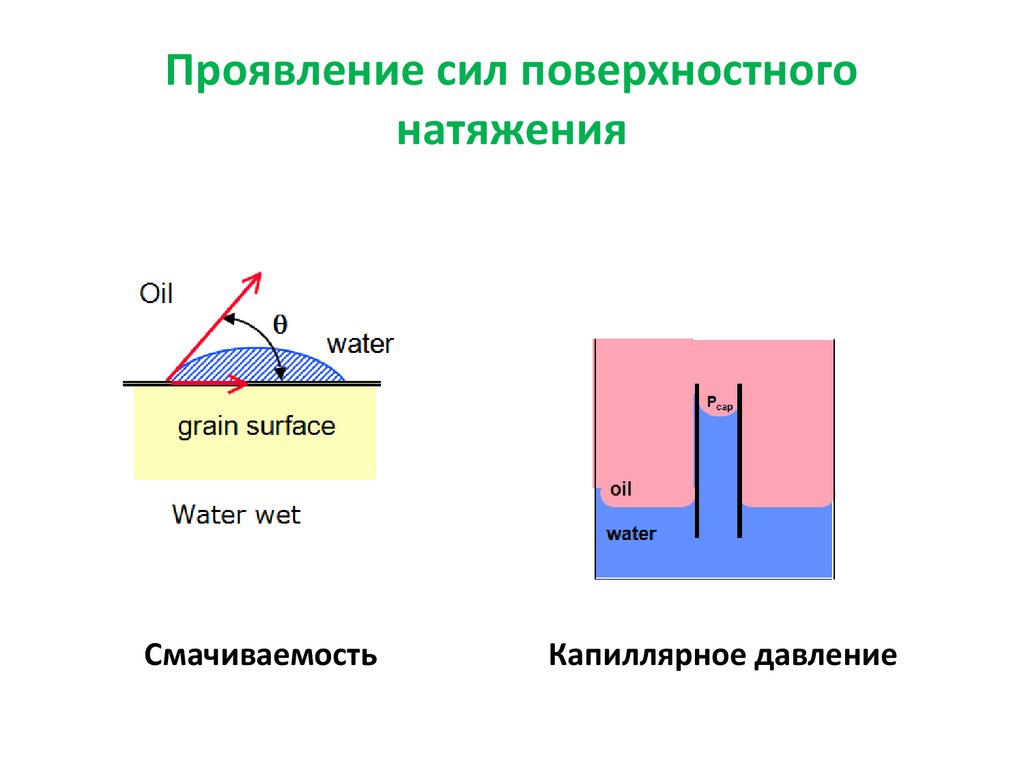
2. Проявление сил поверхностного натяжения
СмачиваемостьКапиллярное давление
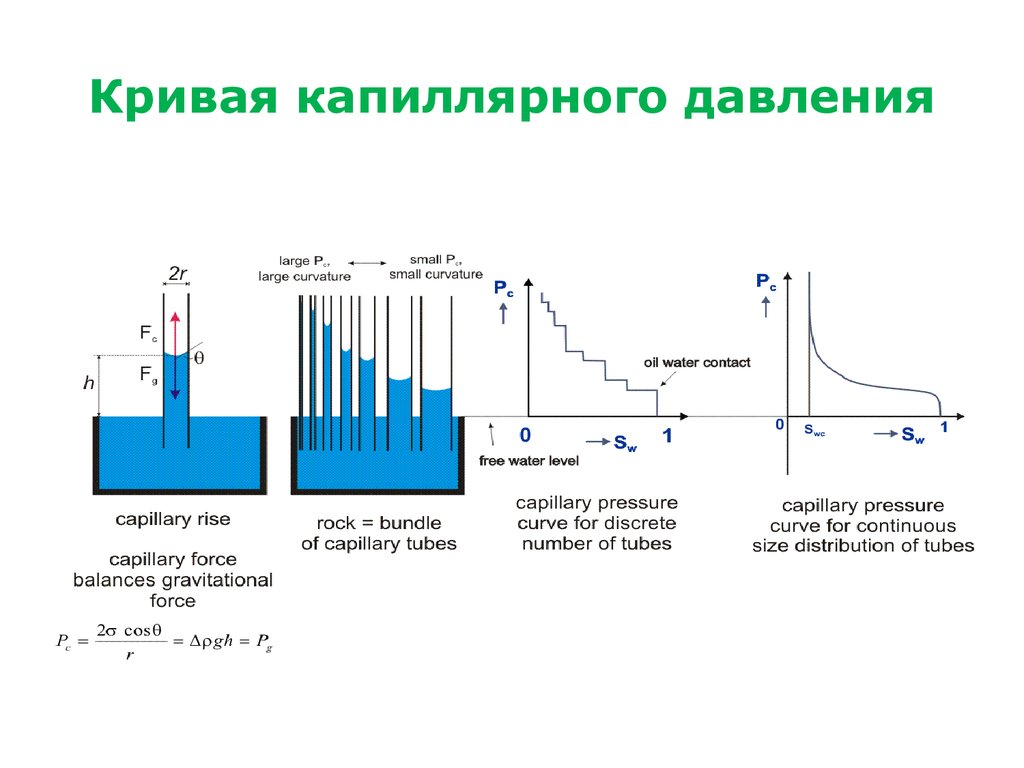
3. Кривая капиллярного давления
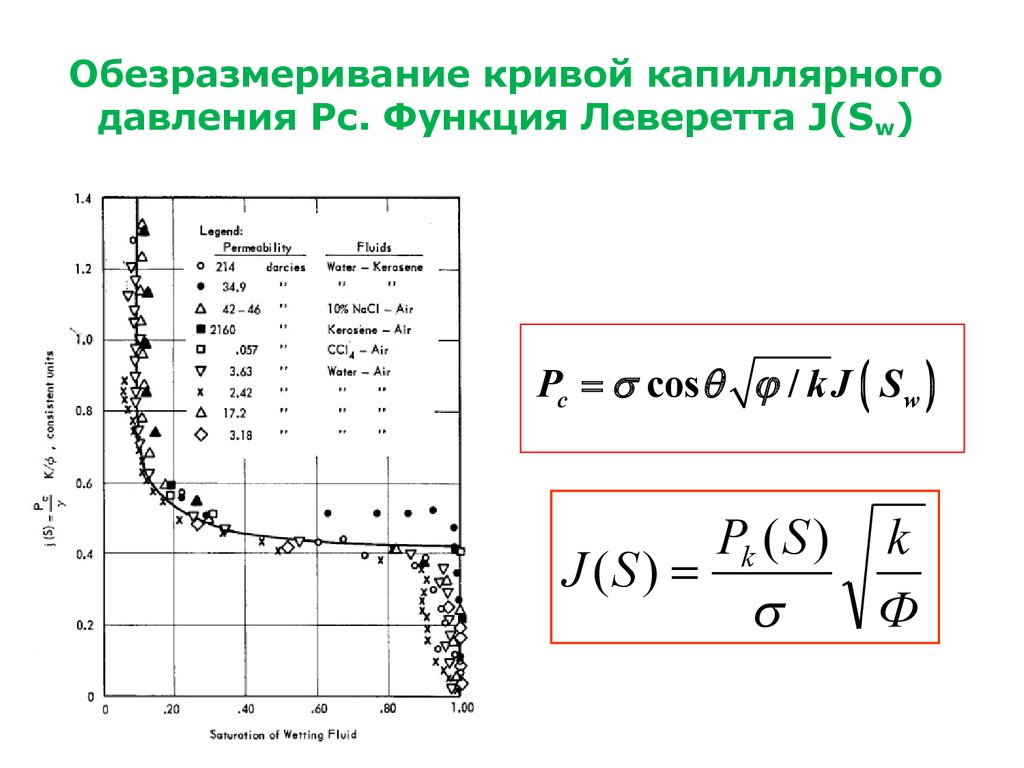
4. Обезразмеривание кривой капиллярного давления Pc. Функция Леверетта J(Sw)
Обезразмеривание кривой капиллярногодавления Pc. Функция Леверетта J(S w)
Pc = s cos q j / k J ( S w )
Pk ( S ) k
J (S ) =
s
Ф
5. Механика многофазных процессов
• Что такое фаза? Что такое компонента?• Приведите примеры многофазного и
многокомпонентного веществ.
6. Интегральные и дифференциальные уравнения сохранения.
7. Условия перехода от интегральных к дифференциальным уравнениям:
- Функции непрерывные,- Объем произвольный,
- Элементарный объем l3<<dV<<L3
8. Характерный размер пор
N r 4 Pq=
8
L
P
q = kS
L
Формула Пуазейля
Формула Дарси
Nr L
m=
=
= nr 2
V
SL
Vпор
2
N r 4 nr 4
k=
=
S8
8
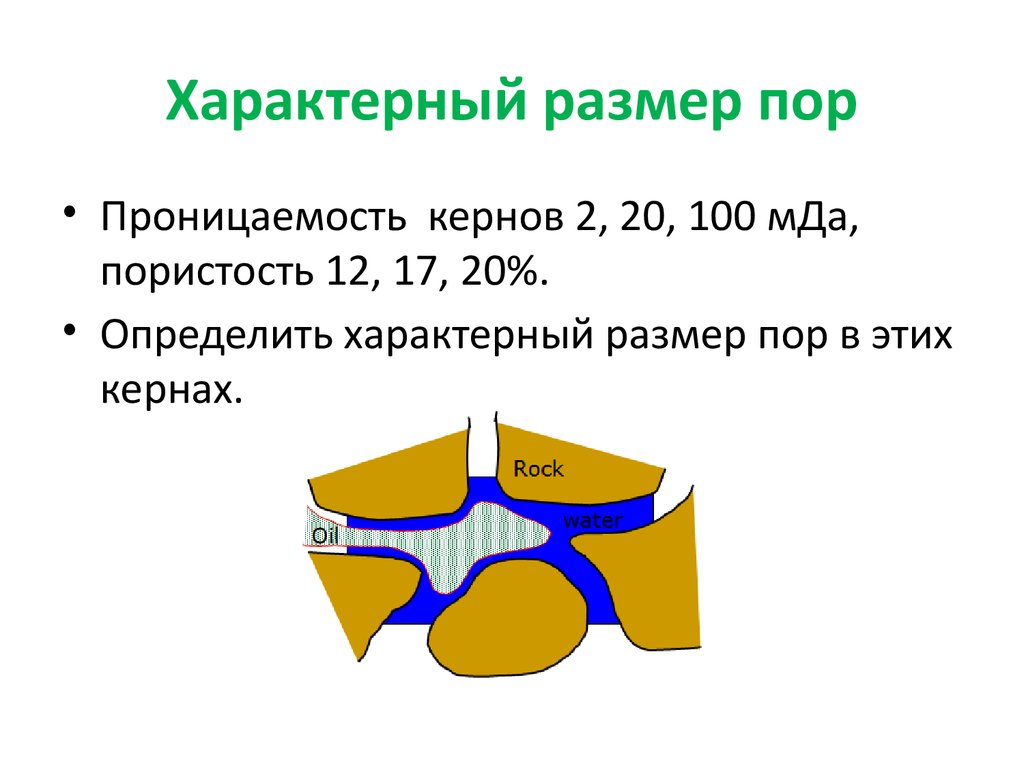
9. Характерный размер пор
• Проницаемость кернов 2, 20, 100 мДа,пористость 12, 17, 20%.
• Определить характерный размер пор в этих
кернах.
10. Примеры, когда переход от интегральных к дифференциальным уравнениям возможен, когда нет.
• Фильтрация воды и нефти в пласте• Фильтрация воды и нефти в керновых
экспериментах
• Движение флюидов в керне с продольной
трещиной
• Движение ганглии нефти по пористой среде
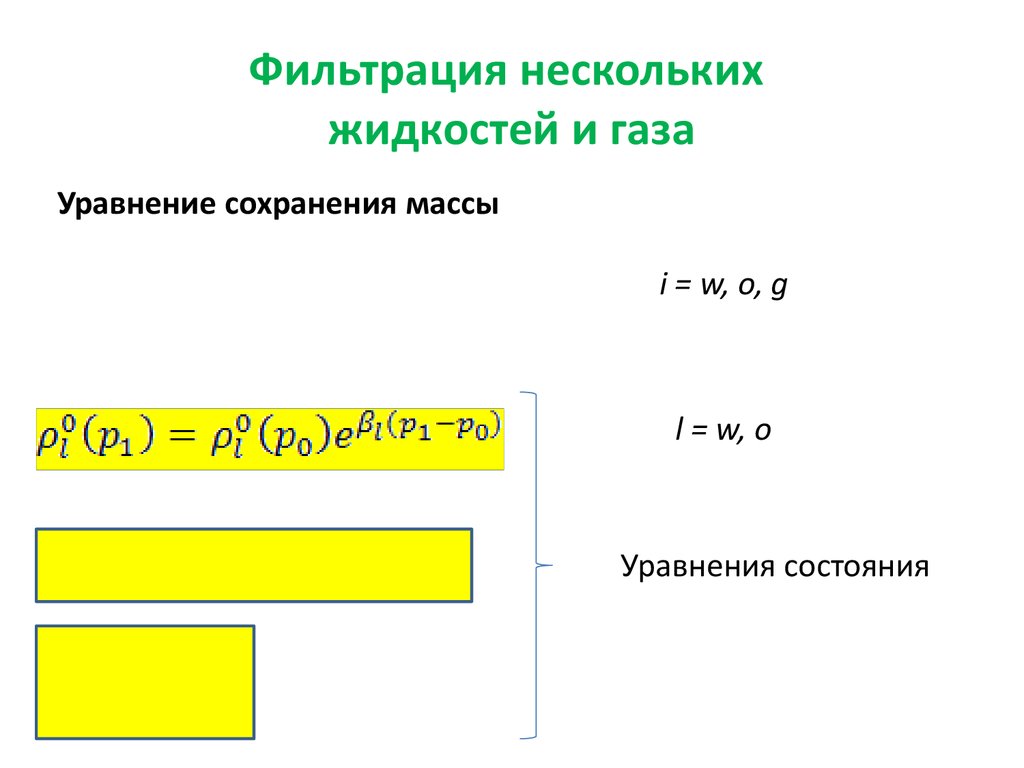
11. Фильтрация нескольких жидкостей и газа
Уравнение сохранения массыi = w, o, g
l = w, o
Уравнения состояния
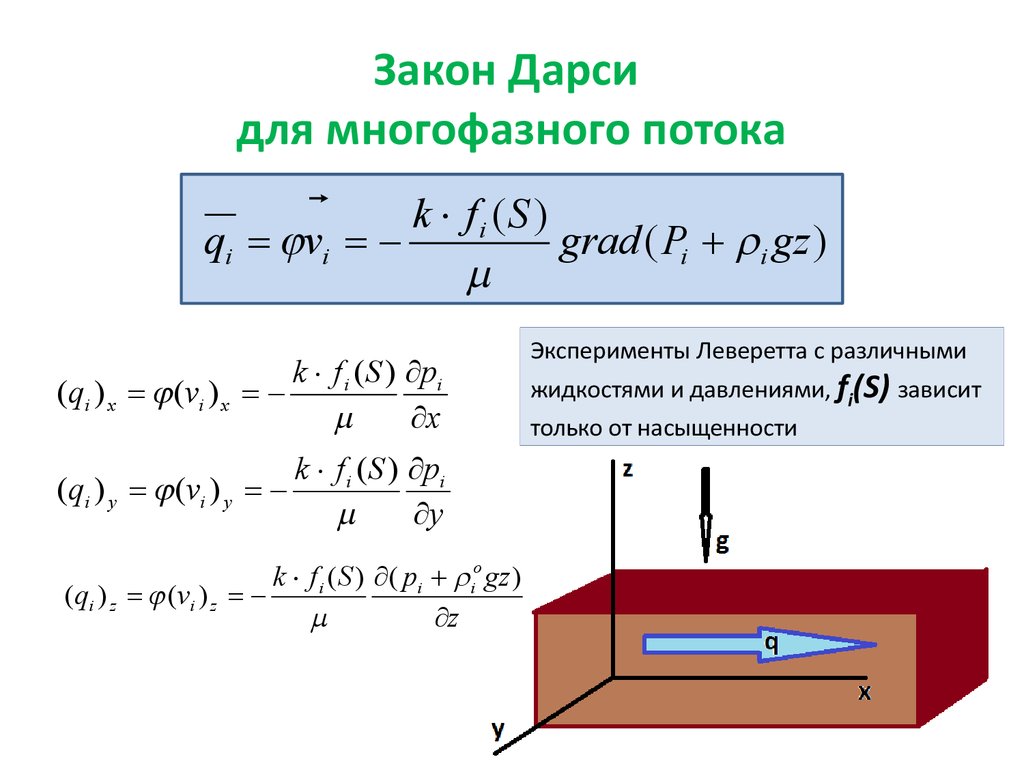
12. Закон Дарси для многофазного потока
k fi (S )qi = jvi =
grad ( Pi i gz )
(qi ) x = j (vi ) x =
k f i ( S ) pi
x
(qi ) y = j (vi ) y =
k f i ( S ) pi
y
k f i ( S ) ( pi io gz )
(qi ) z = j (vi ) z =
z
Эксперименты Леверетта с различными
жидкостями и давлениями, fi(S) зависит
только от насыщенности
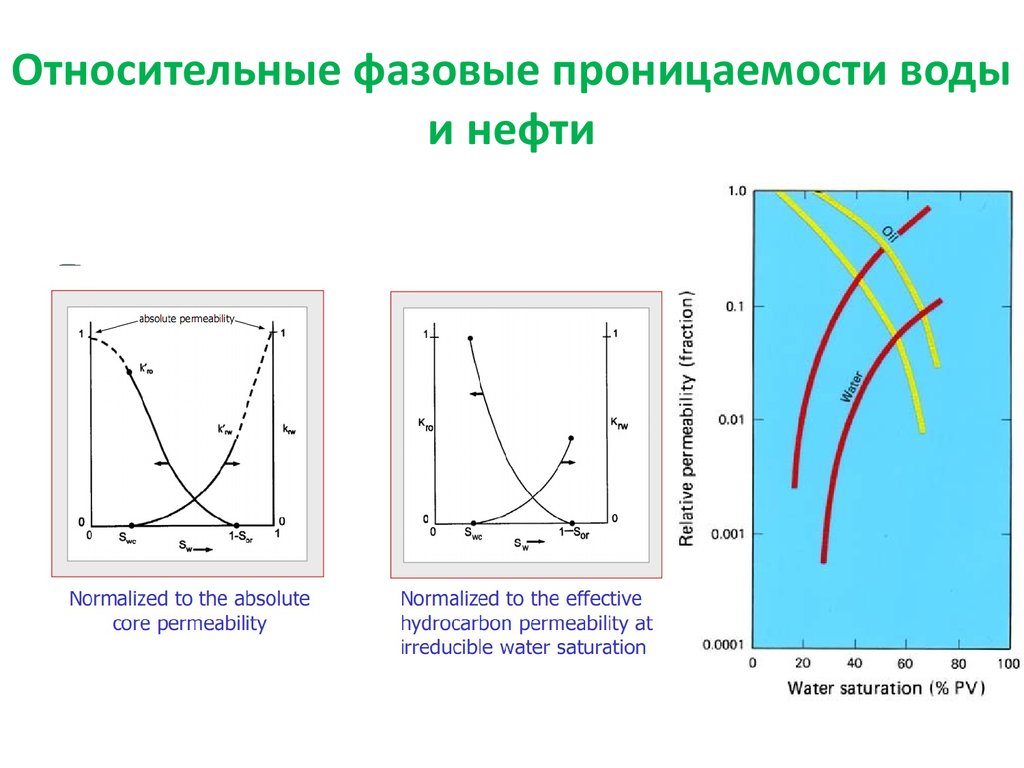
13. Относительные фазовые проницаемости воды и нефти
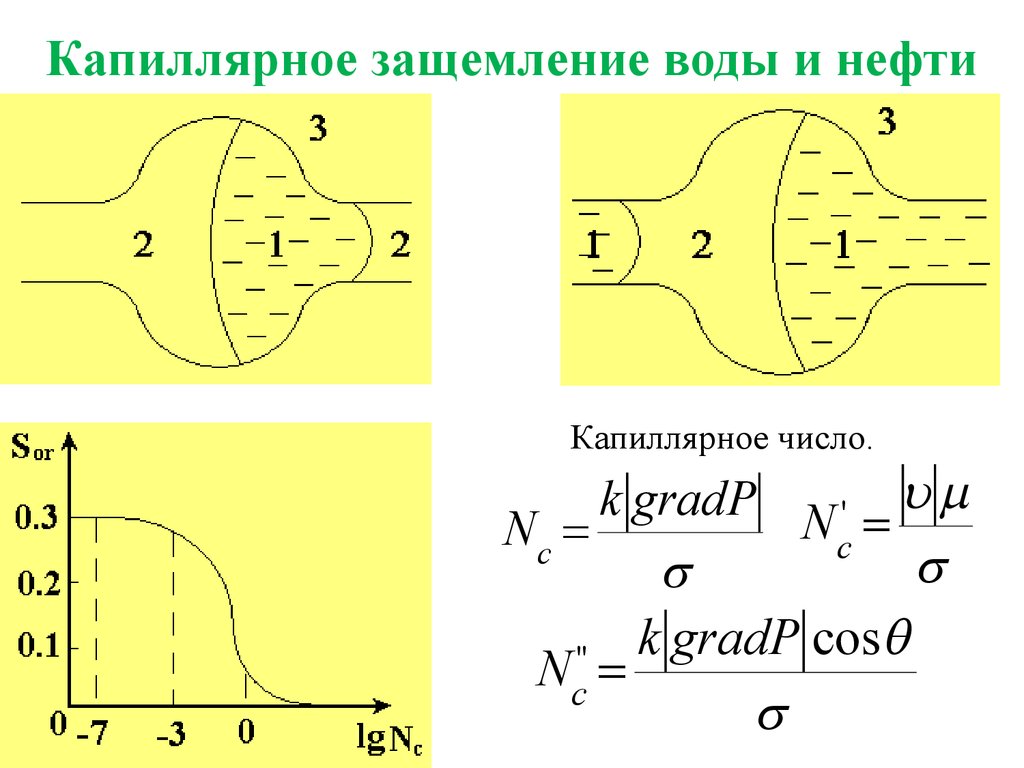
14. Капиллярное защемление воды и нефти
Капиллярное число.k gradP N ' =
Nc =
c
s
s
k gradP cosq
'
'
Nc =
s
15.
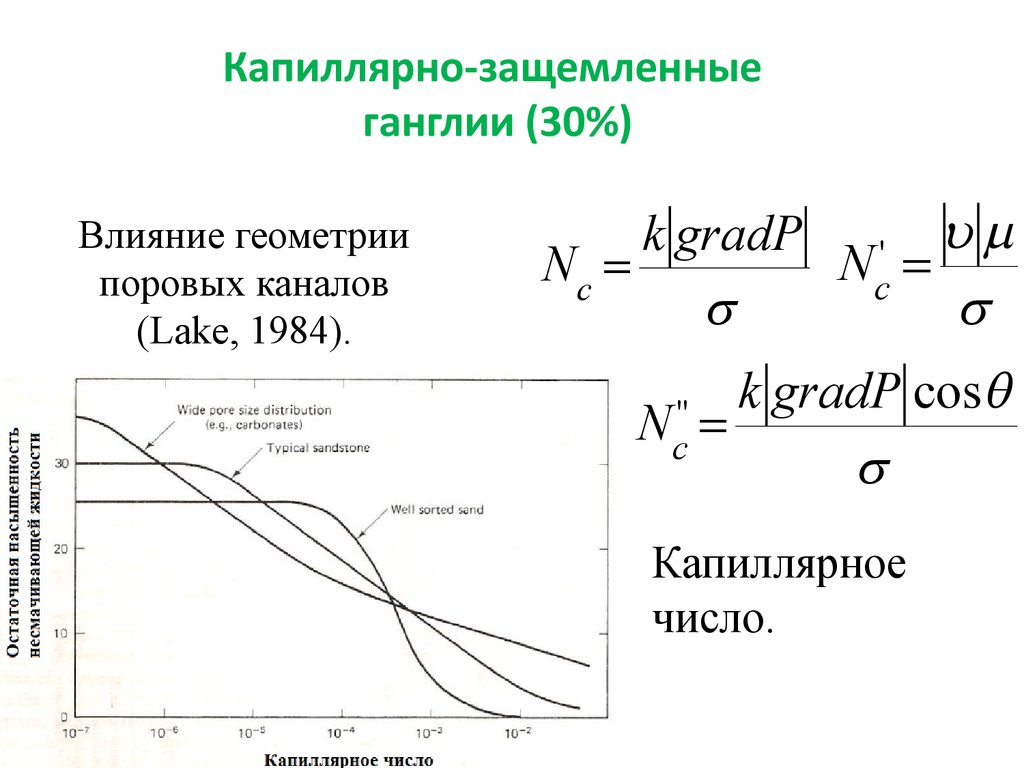
Капиллярно-защемленныеганглии (30%)
Влияние геометрии
поровых каналов
(Lake, 1984).
k gradP
'
Nc =
Nc =
s
s
k
'
'
Nc =
gradP cosq
s
Капиллярное
число.
16. Эксперименты по растворению породы и визуализации ганглей (Chatzis et.al. 1983)
ЭКСПЕРИМЕНТЫ ПО РАСТВОРЕНИЮ ПОРОДЫ ИВИЗУАЛИЗАЦИИ ГАНГЛЕЙ (CHATZIS ET.AL. 1983)
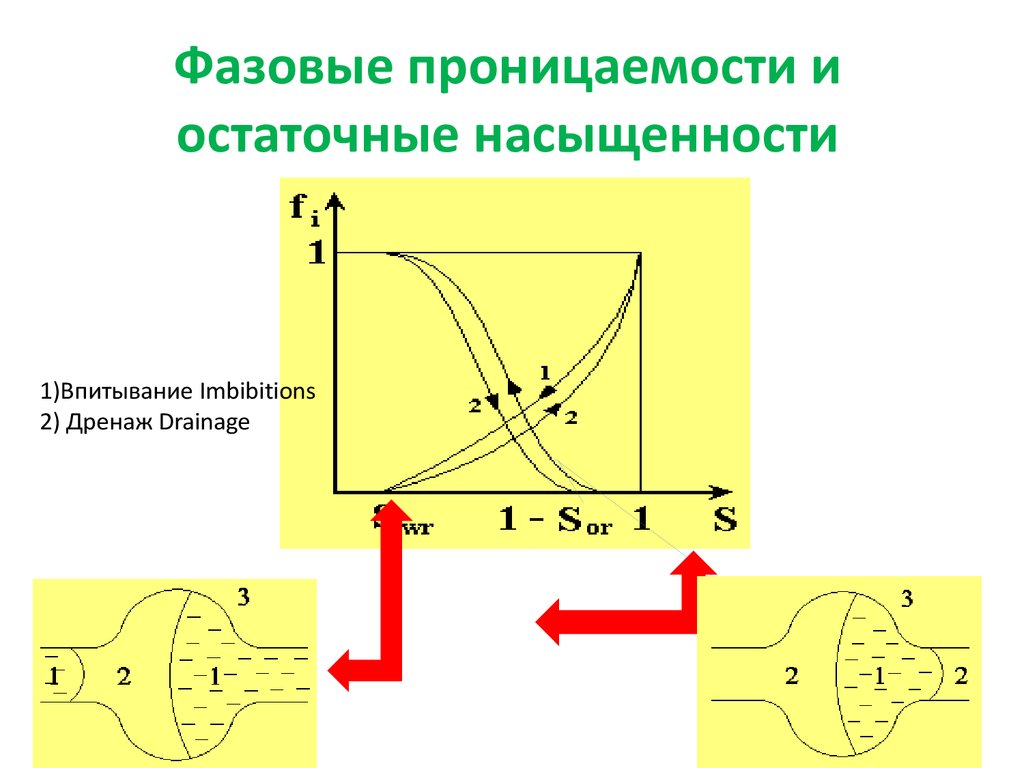
17. Фазовые проницаемости и остаточные насыщенности
1)Впитывание Imbibitions2) Дренаж Drainage
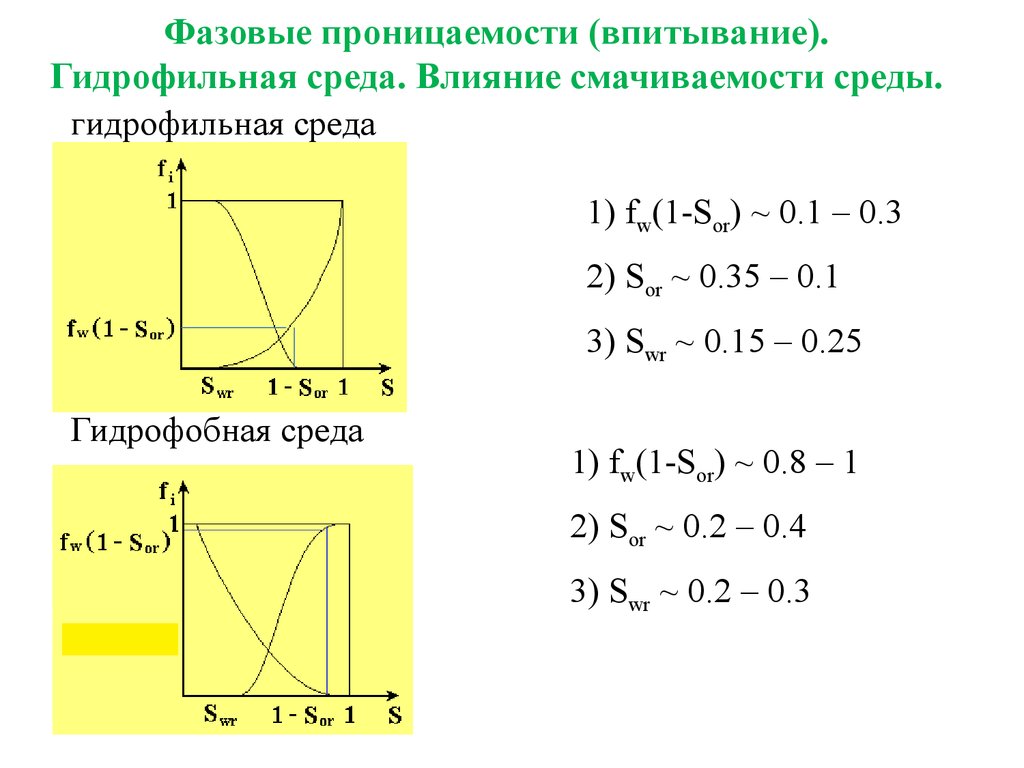
18. Фазовые проницаемости (впитывание). Гидрофильная среда. Влияние смачиваемости среды.
гидрофильная среда1) fw(1-Sor) ~ 0.1 – 0.3
2) Sor ~ 0.35 – 0.1
3) Swr ~ 0.15 – 0.25
Гидрофобная среда
1) fw(1-Sor) ~ 0.8 – 1
2) Sor ~ 0.2 – 0.4
3) Swr ~ 0.2 – 0.3
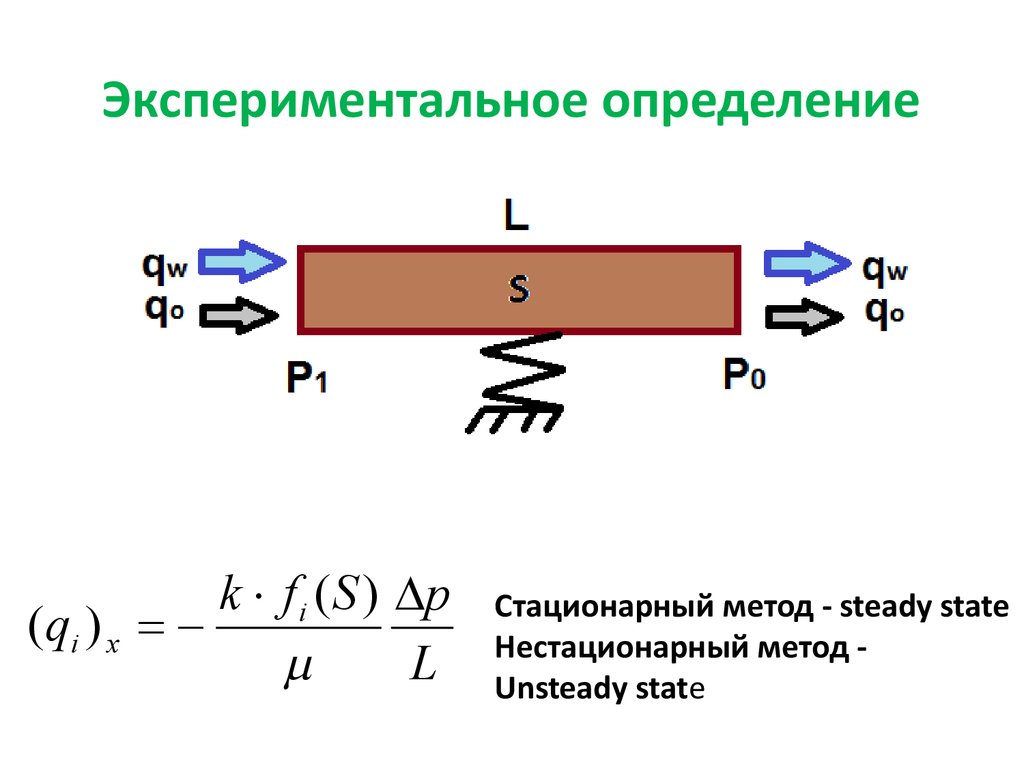
19. Экспериментальное определение
k f i ( S ) p(qi ) x =
L
Стационарный метод - steady state
Нестационарный метод Unsteady state
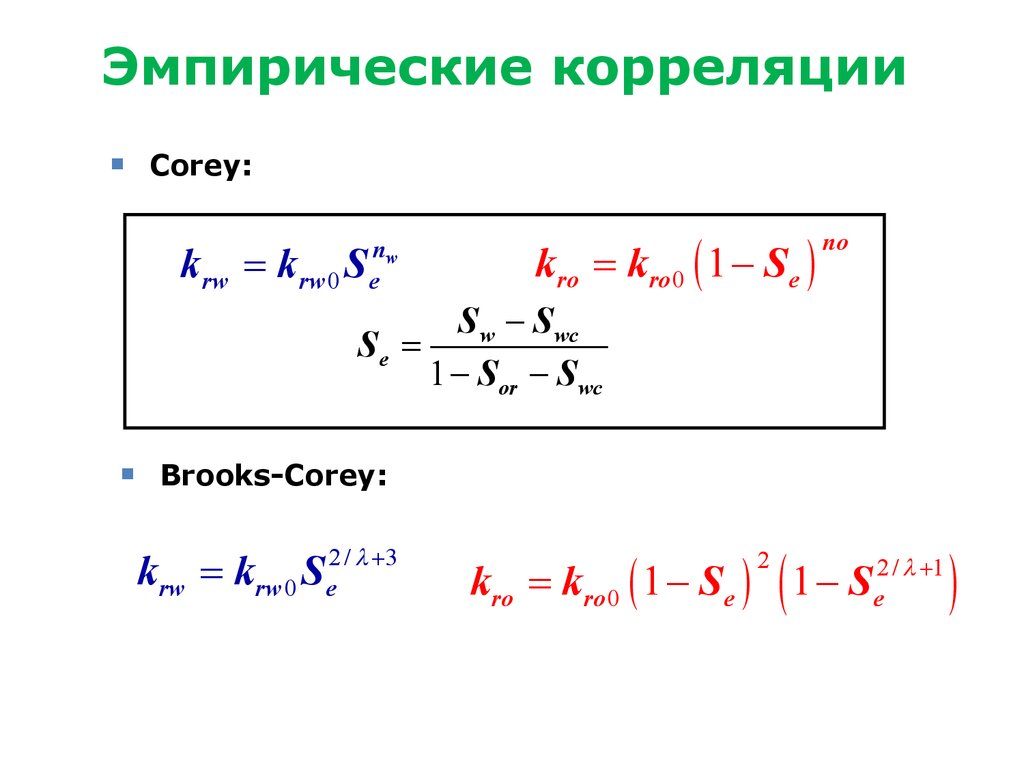
20. Эмпирические корреляции
Corey:krw = krw 0 S
nw
e
kro = kro 0 ( 1 Se )
no
S w S wc
Se =
1 Sor S wc
Brooks-Corey:
krw = krw 0 Se2 / l 3
(
kro = kro 0 ( 1 Se ) 1 Se2 / l 1
2
)
21.
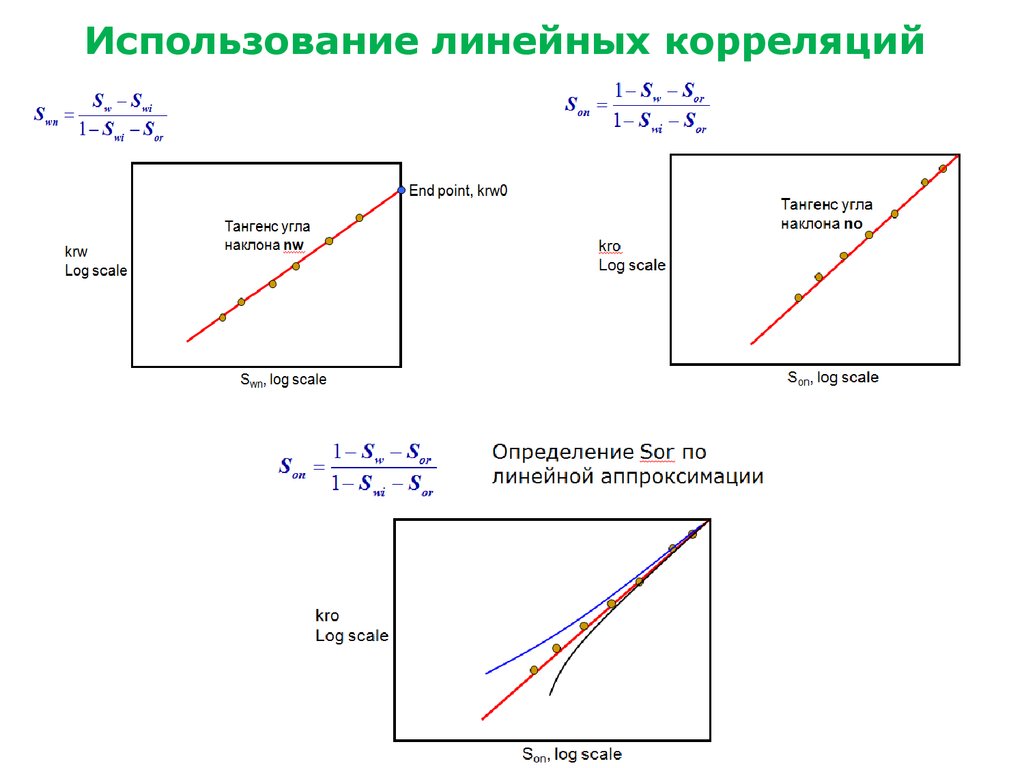
Использование линейных корреляций22.
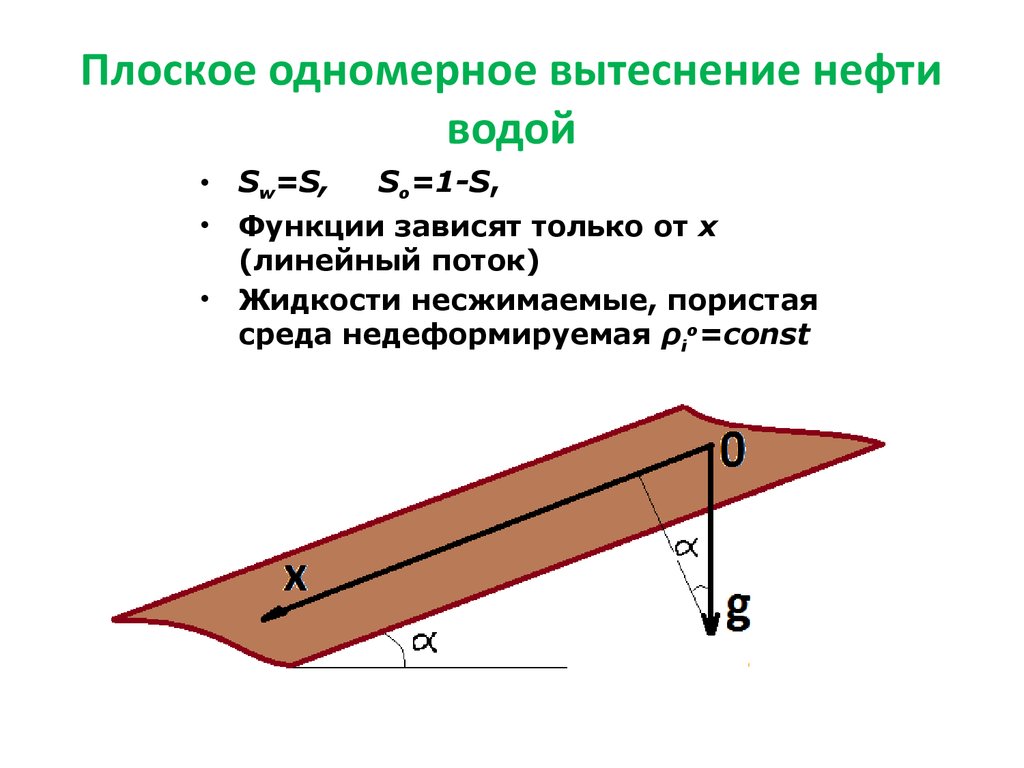
Плоское одномерное вытеснение нефтиводой
Sw=S,
So=1-S,
Функции зависят только от x
(линейный поток)
Жидкости несжимаемые, пористая
среда недеформируемая ρio=const
23. Плоское одномерное вытеснение нефти водой
S (jvw )j
=0
t
x
(1 S ) (jvo )
j
=0
t
x
Уравнения сохранения массы воды и нефти
k f i ( S ) ( pi io gx sin )
j vi =
i
x
s
po p w =
J (S )
k /
Закон Дарси с учетом
сил гравитации
Капиллярное
давление
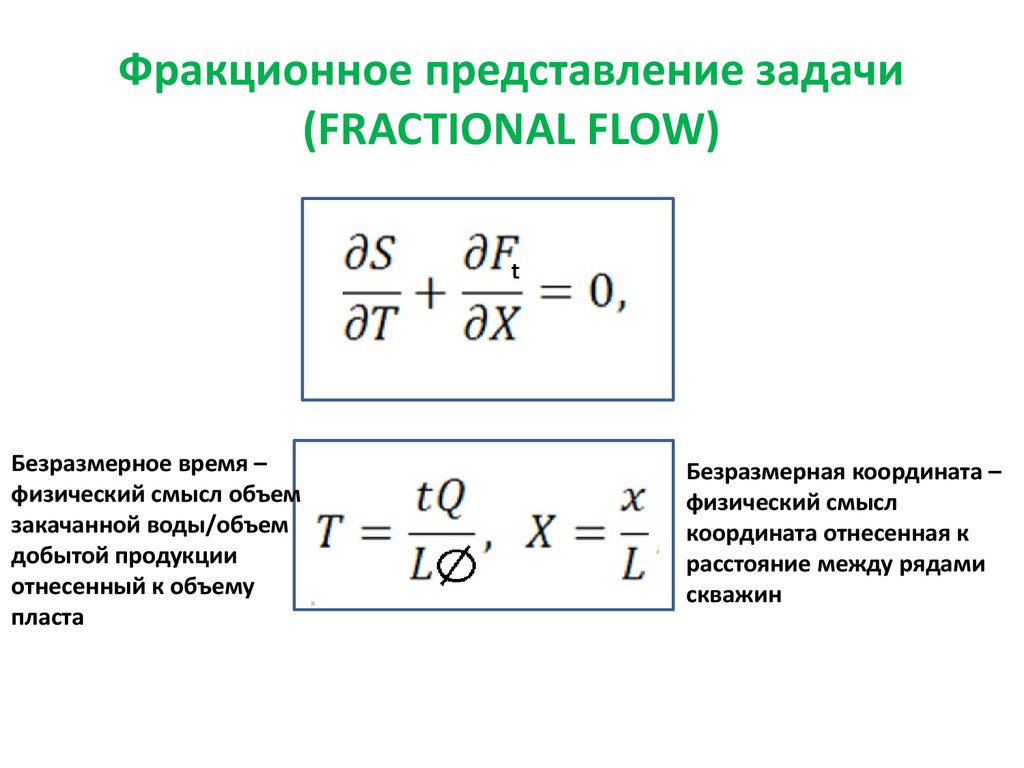
24. Фракционное представление задачи (FRACTIONAL FLOW)
Q = jvw jvoОбщий поток флюидов
Доля воды в общем потоке
(обобщенная функция Баклея-Леверетта)
f w (S ) / w
F (S ) =
,
f w (S ) / w f o (S ) / o
25. Безразмерные комплексы подобия
ksNc =
,
oQL k / j
Соотношение
капиллярного
давления к общей
депрессии на пласт
k g
Ng =
oQ
Отношение сил
тяжести к гидродинамическим силам
26. ПРАКТИКА
Скорость общего потока Q=50м/год, абсолютнаяпроницаемость 100 мД, пористость 0.2, разность
плотностей 200кг/м3, гравитационная постоянная 10
м/с2, коэффициент поверхностного натяжения
30мН/м
• Оценить влияние сил гравитации Ng
• Оценить влияние капиллярных сил Nc
• Сделаем выводы о влиянии приведенных сил на
процесс
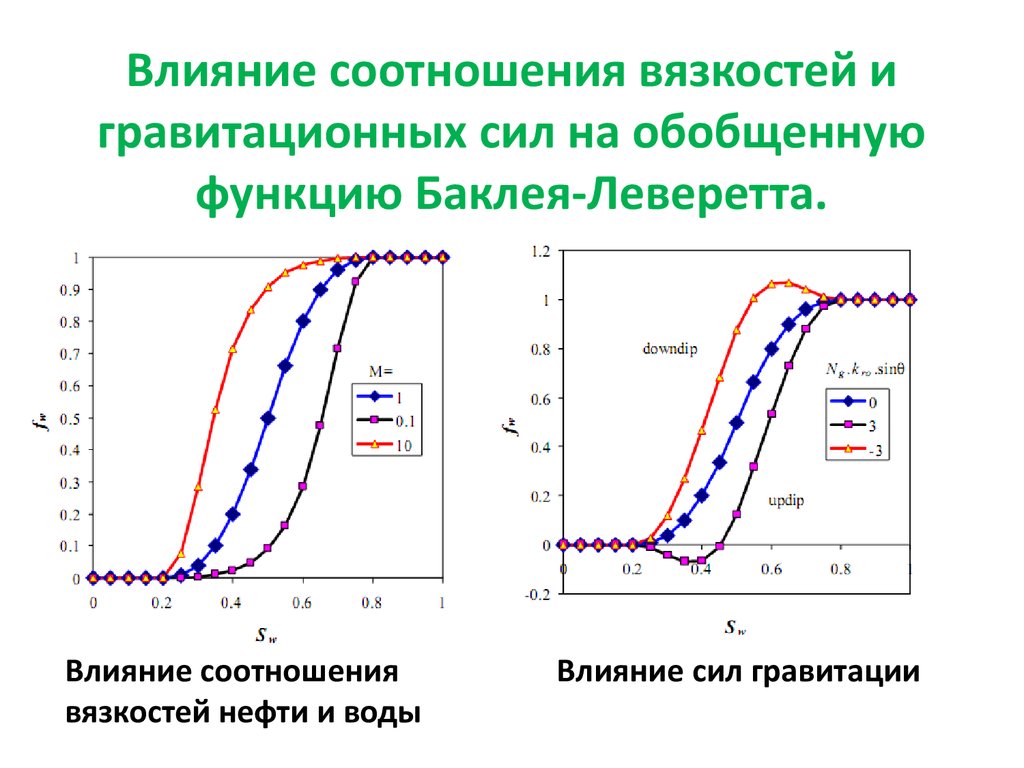
27. Влияние соотношения вязкостей и гравитационных сил на обобщенную функцию Баклея-Леверетта.
Влияние соотношениявязкостей нефти и воды
Влияние сил гравитации
28. Фракционное представление задачи (FRACTIONAL FLOW)
Безразмерное время –физический смысл объем
закачанной воды/объем
добытой продукции
отнесенный к объему
пласта
Безразмерная координата –
физический смысл
координата отнесенная к
расстояние между рядами
скважин
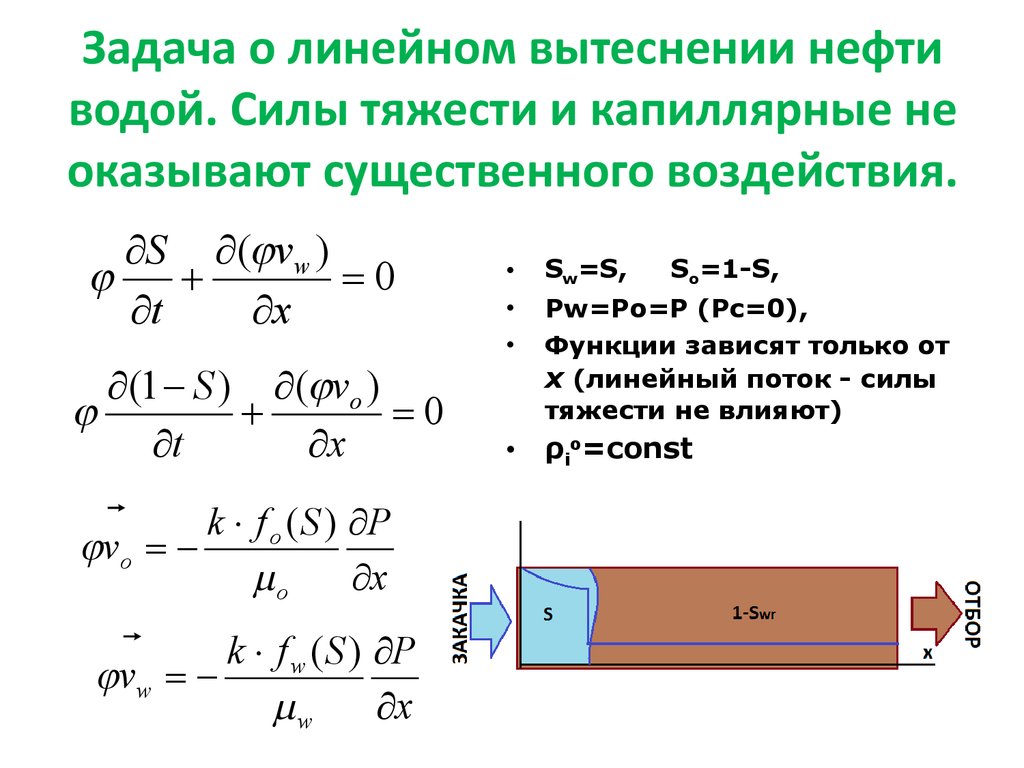
29. Задача о линейном вытеснении нефти водой. Силы тяжести и капиллярные не оказывают существенного воздействия.
S (jvw )j
=0
t
x
(1 S ) (jvo )
j
=0
t
x
k f o ( S ) P
jvo =
o
x
k f w ( S ) P
jvw =
w
x
Sw=S,
So=1-S,
ρio=const
Pw=Po=P (Pc=0),
Функции зависят только от
x (линейный поток - силы
тяжести не влияют)
30. Понимание того, что мы считаем и прогнозируем складывается из того, что учитывается, что нет.
31. Теория одномерного вытеснения нефти водой
Безразмерные координаты:T– объем закачки на объем пор,
X-относительное расстояние от линии
нагнетания до линии отбора
Функция Баклея-Леверетта – доля
воды в потоке (на выходе X=1 –
обводненность.
Решение зависит только от
безразмерных комплексов подобия:
соотношения вязкостей и остаточные
насыщенностей
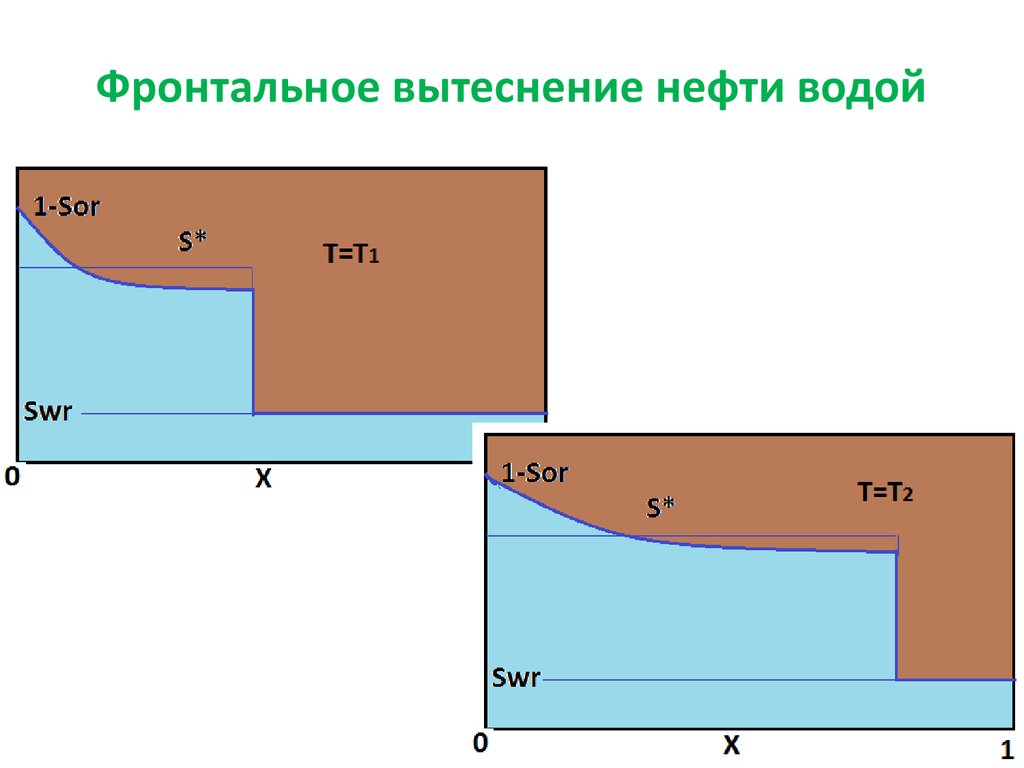
32. Фронтальное вытеснение нефти водой
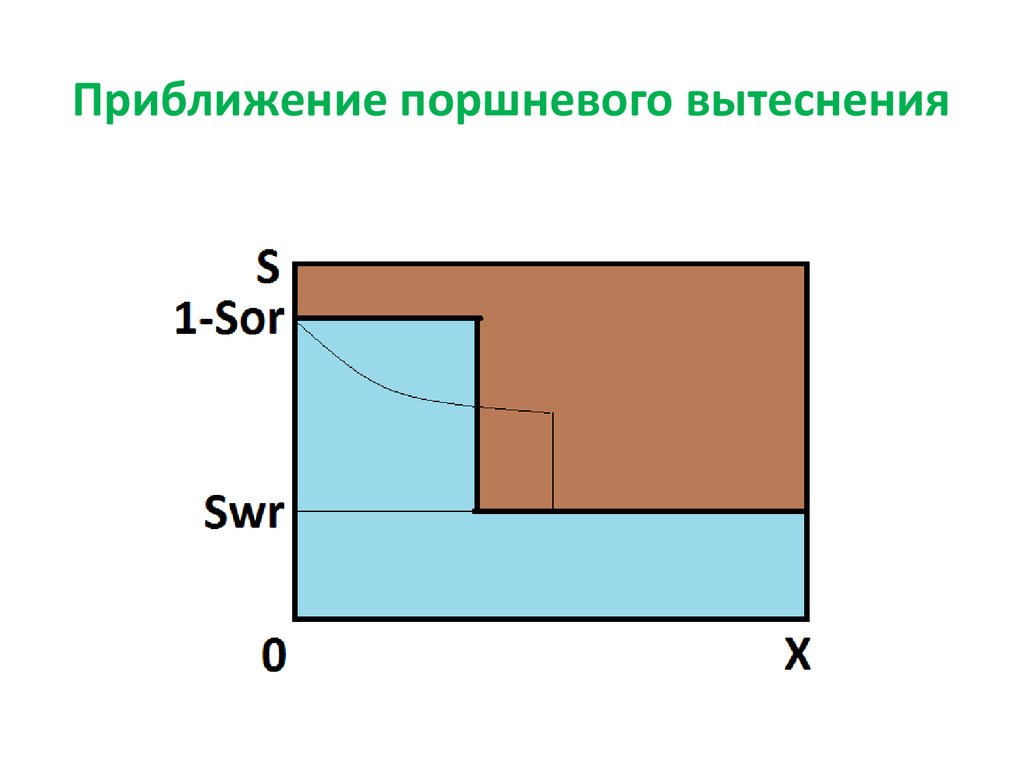
33. Приближение поршневого вытеснения
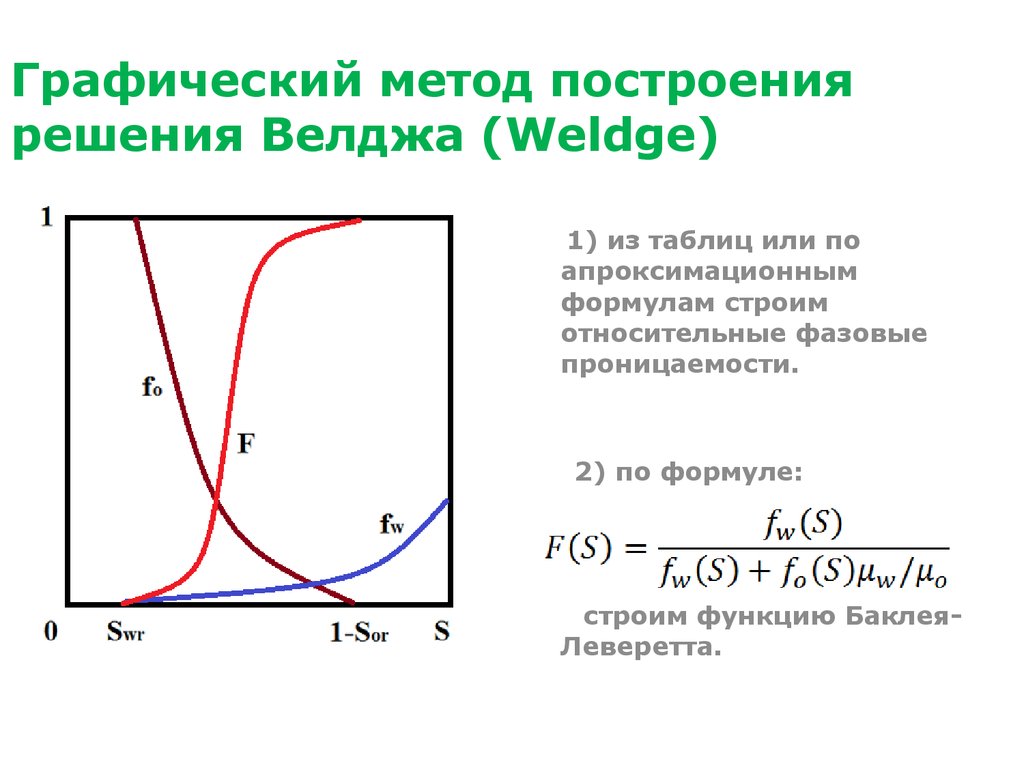
34. Графический метод построения решения Велджа (Weldge)
1) из таблиц или поапроксимационным
формулам строим
относительные фазовые
проницаемости.
2) по формуле:
строим функцию БаклеяЛеверетта.
35.
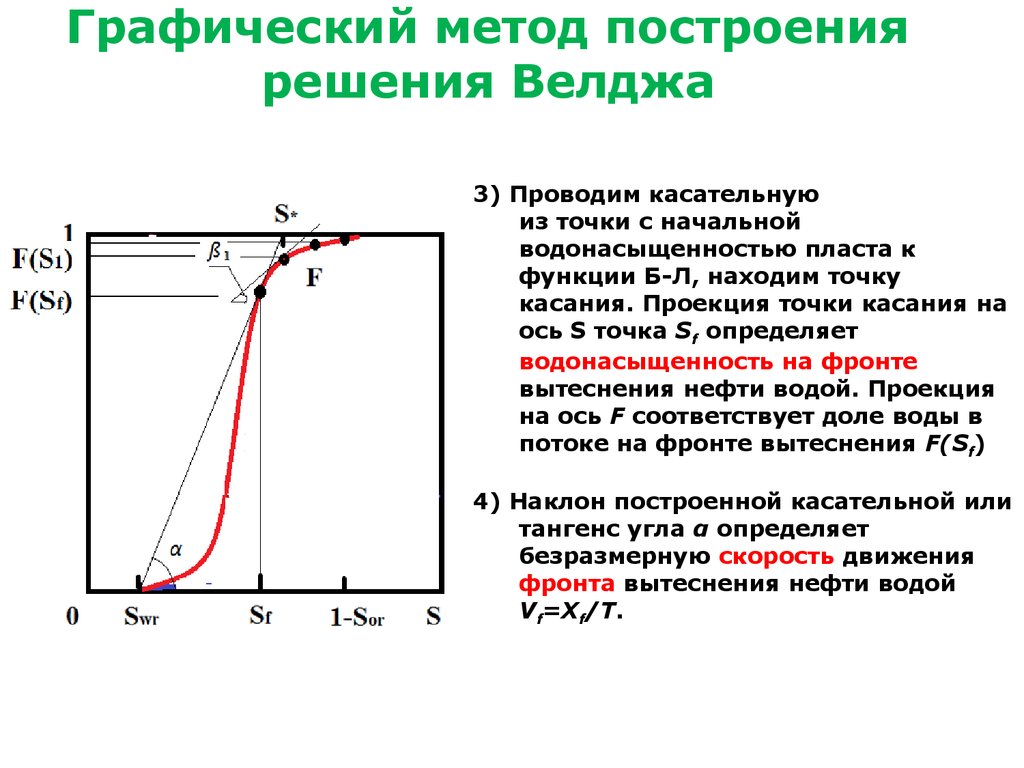
Графический метод построениярешения Велджа
3) Проводим касательную
из точки с начальной
водонасыщенностью пласта к
функции Б-Л, находим точку
касания. Проекция точки касания на
ось S точка Sf определяет
водонасыщенность на фронте
вытеснения нефти водой. Проекция
на ось F соответствует доле воды в
потоке на фронте вытеснения F(Sf)
4) Наклон построенной касательной или
тангенс угла α определяет
безразмерную скорость движения
фронта вытеснения нефти водой
Vf=Xf/T.
36.
Графический метод построениярешения Велджа
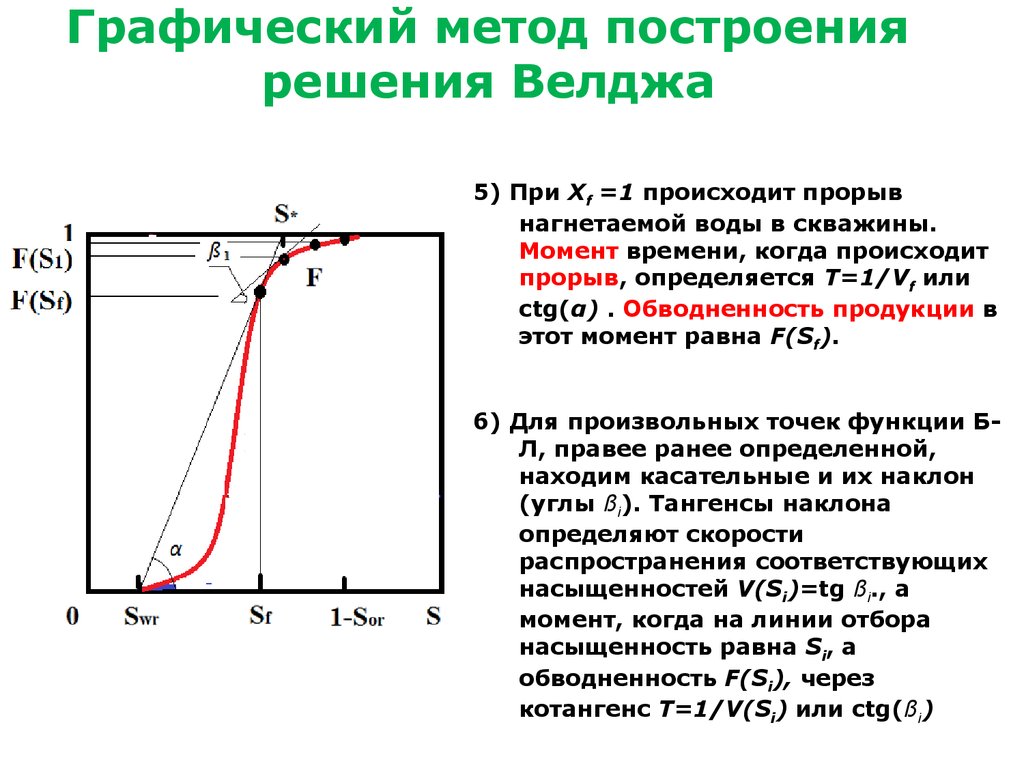
5) При Xf =1 происходит прорыв
нагнетаемой воды в скважины.
Момент времени, когда происходит
прорыв, определяется T=1/Vf или
ctg(α) . Обводненность продукции в
этот момент равна F(Sf).
6) Для произвольных точек функции БЛ, правее ранее определенной,
находим касательные и их наклон
(углы ßi). Тангенсы наклона
определяют скорости
распространения соответствующих
насыщенностей V(Si)=tg ßi., а
момент, когда на линии отбора
насыщенность равна Si, а
обводненность F(Si), через
котангенс T=1/V(Si) или ctg(ßi)
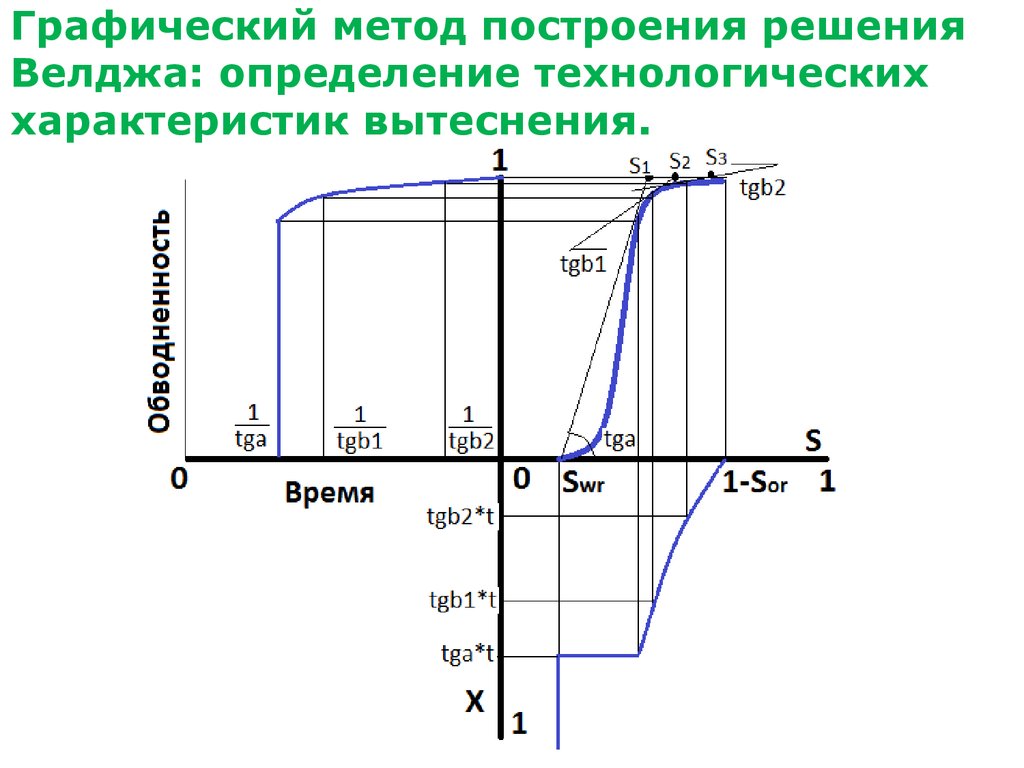
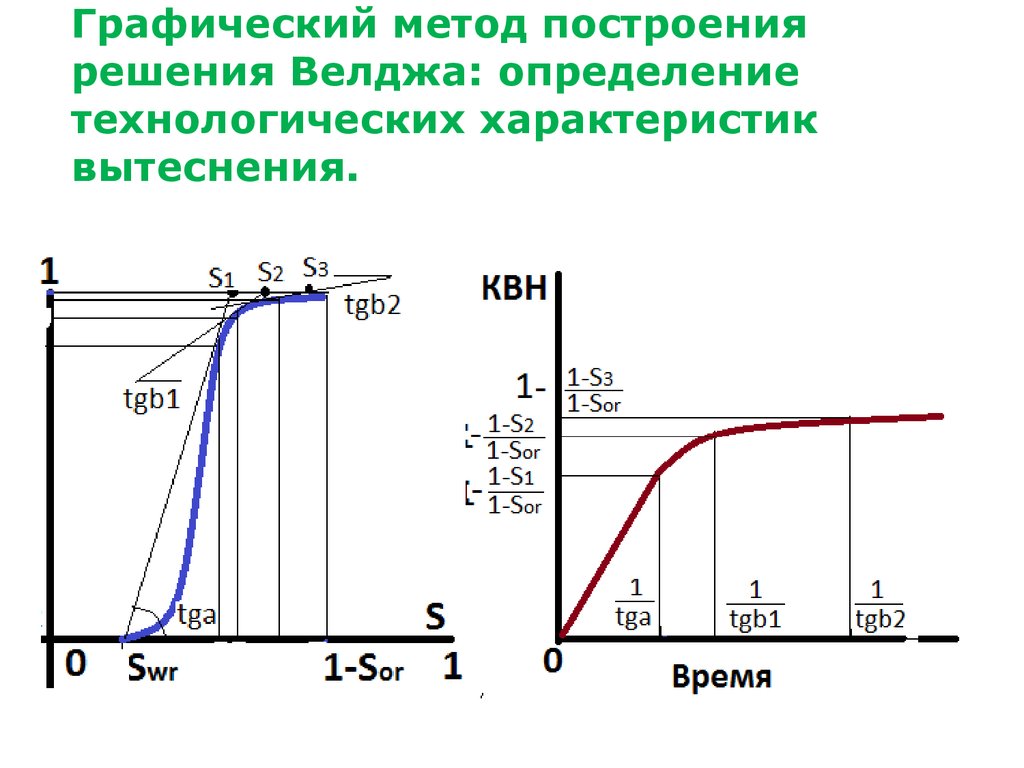
37. Графический метод построения решения Велджа: определение технологических характеристик вытеснения.
38. Графический метод построения решения Велджа: определение технологических характеристик вытеснения.
39. Переход к размерным единицам
40. Практика
Построим график функции Баклея-Леверетта от водонасыщенности при вязкости воды 1, а нефти 5 и 20 сПз иопределим решение задач о вытеснении нефти из пласта с
водонасыщенностью SWR=0.2. Построим зависимость доли
воды в потоке продукции от беразмерного времени.
Сделаем выводы об особенностях вытеснения высоковязкой
нефти
41. Практика
• Расстояние между рядом нагнетательных идобывающих скважин 700м, скорость потока
воды 100 м/год, пористость 0.2.
• Определить положение фронта воды через 6
месяцев.
• Определить скорость движения фронта воды
м/год.
42. Практика
Построим график функции Баклея-Леверетта отводонасыщенности при вязкости воды 1, а нефти
5 сПз и определим решение задач о вытеснении
нефти из пласта с водонасыщенностью SWR=0.3
Сделаем вывод об особенностях процесса в
гидрофобных коллекторах
43. ПРАКТИКА
• Для сводовой залежи сопоставить эффективность системзаводнения, в которых а) нагнетательные скважины
расположены в наиболее высокой части залежи, а
добывающие по периферии, б) нагнетательные скважины
расположены по периферии, а в сводовой части
добывающие.
Для этого:
• Определить водонасыщенность на фронте вытеснения Sf
для обеих систем, по графикам, представленным ранее.
• Определить количество закачанной воды в пласт по
отношению к поровому объему пласта на момент прорыва
фронта вытеснения в добывающие скважины, также для
обеих систем.
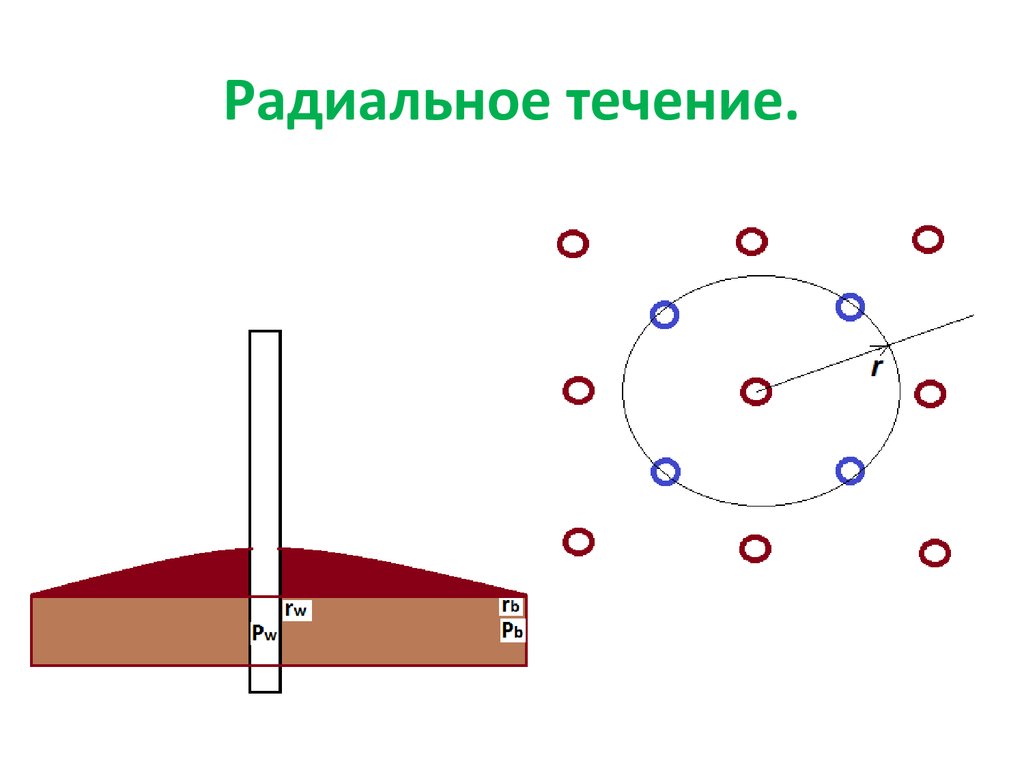
44. Радиальное течение.
45. Осесимметричная фильтрация
Sj
div(jSvw ) = 0
t
(1 S )
j
div (j (1 S )vo ) = 0
t
S 1
j
(rjSvw ) = 0
t r r
j
(1 S ) 1
(rj (1 S )vo ) = 0
t
r r
k f w (S )
jvw =
grad P
w
k f w ( S ) P
jvw =
w
r
k f o (S )
jvo =
grad P
o
k f o ( S ) P
jvo =
o r
46. Фракционное представление
r (jvw jvo ) = const , 2 rh (jvw jvo ) = Q,Q = 2 rw h(jvw ) на нагнетательной скважине
Qt
T=
,
2
2
j (rb rw )h
r 2 rw2
X= 2 2
rb rw
47. Переход к размерным единицам
QtT=
j (rb2 rw2 )h
r r
X= 2
rb r
2
2
w
2
w
j (r r )h
= t =
T,
Q
2
b
2
w
2
= r = rw (rb2 rw2 ) X ,
X j h(r 2 rw2 )
V= =
=
T
Qt
(r 2 rw2 )
Q X
=
t
j h T
48. Практика
Построим график функции Баклея-Леверетта от водонасыщенности при вязкости воды 1, а нефти 5 и 20 сПз иопределим решение задач о вытеснении нефти из пласта с
водонасыщенностью SWR=0.2. Построим зависимость доли
воды в потоке продукции от беразмерного времени.
49. Практика
• Для пятиточечной системы разработки срасстоянием между добывающими
скважинами 700м, скорость закачки воды в
нагнетательную скважину 300 м3/сут,
пористость 0.2, радиус скважины 0.1м
• Определить положение фронта воды через 6
месяцев.
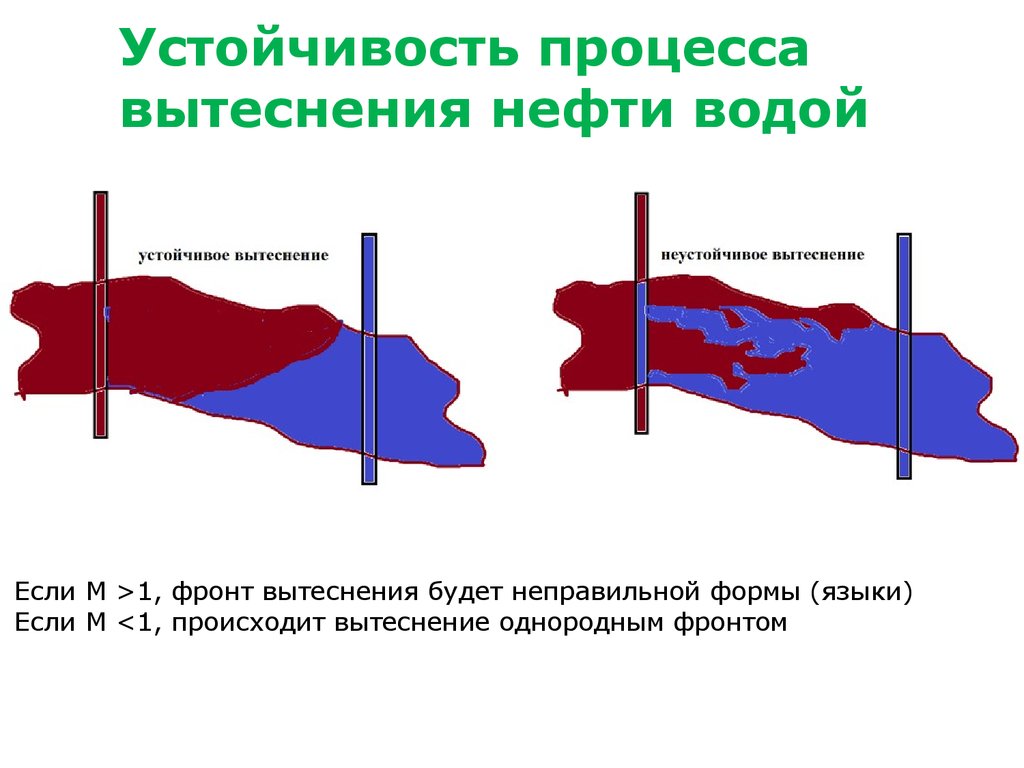
50. Устойчивость процесса вытеснения нефти водой
ВодаВода
Нефть
Нефть
Если M >1, фронт вытеснения будет неправильной формы (языки)
Если M <1, происходит вытеснение однородным фронтом
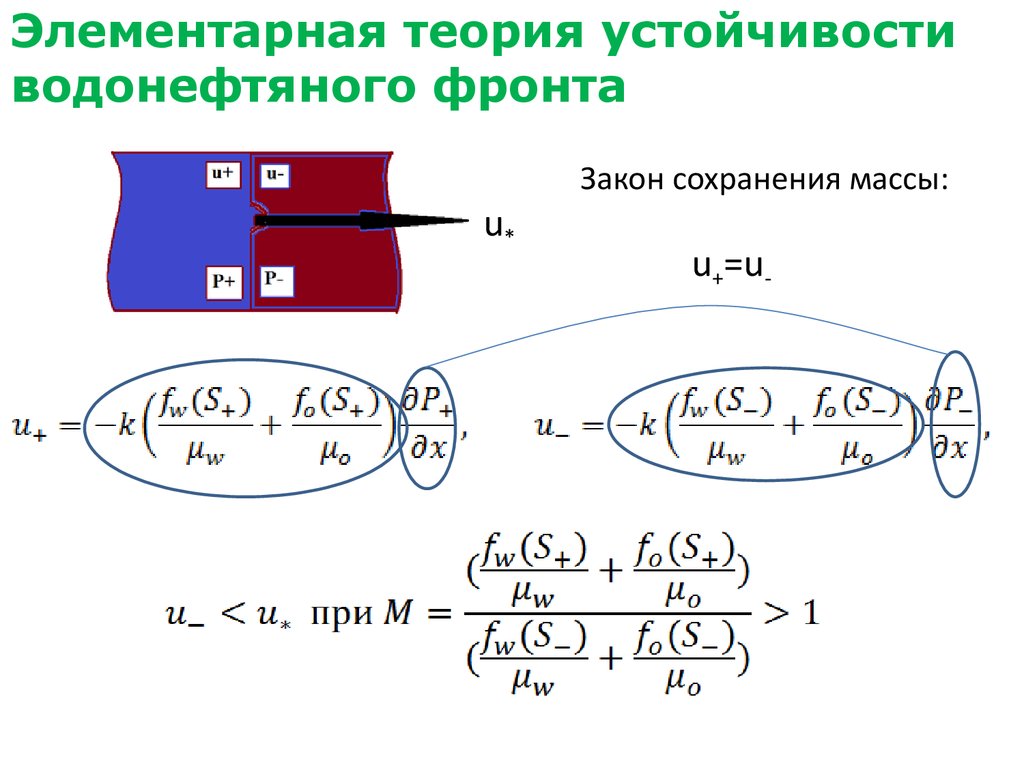
51. Элементарная теория устойчивости водонефтяного фронта
u*Закон сохранения массы:
u+=u-
52. Практика
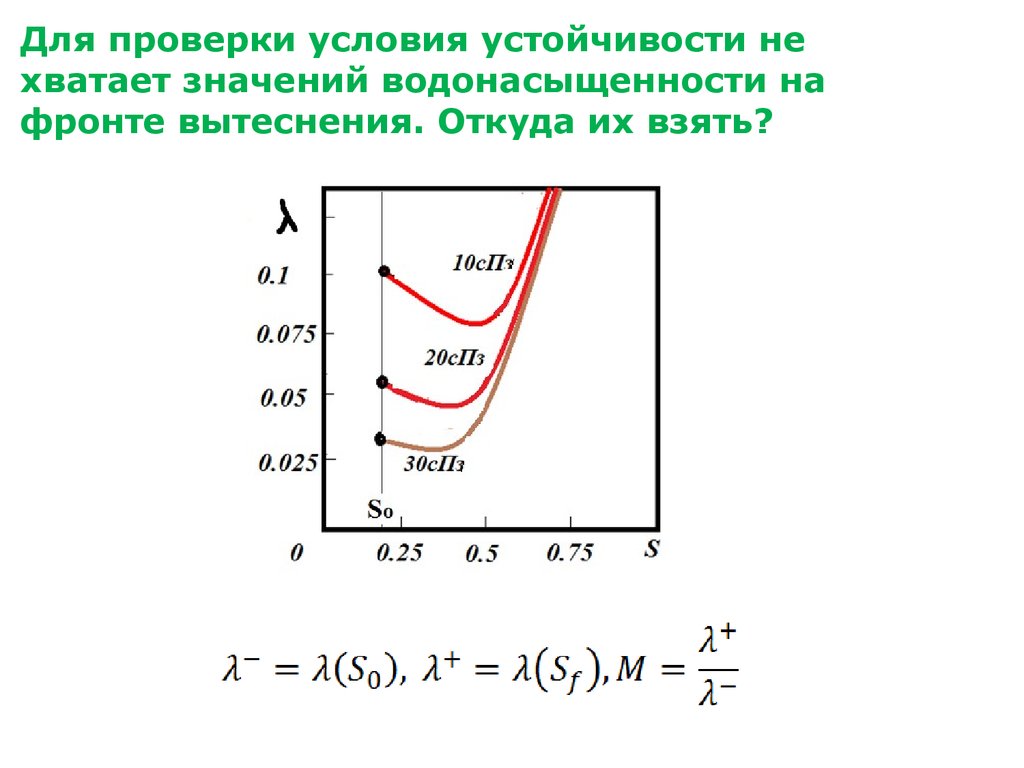
Построим график подвижности потока λ от водонасыщенности при вязкости воды 1, а нефти10, 20 и 30 сПз. Построим решения задачи Б-Л для этих
вязкостей. Нанесем определенные из решения точки S + = Swr
=0.2 и S-=Sf Проверим условие устойчивости для всех
решений.
53. Для проверки условия устойчивости не хватает значений водонасыщенности на фронте вытеснения. Откуда их взять?
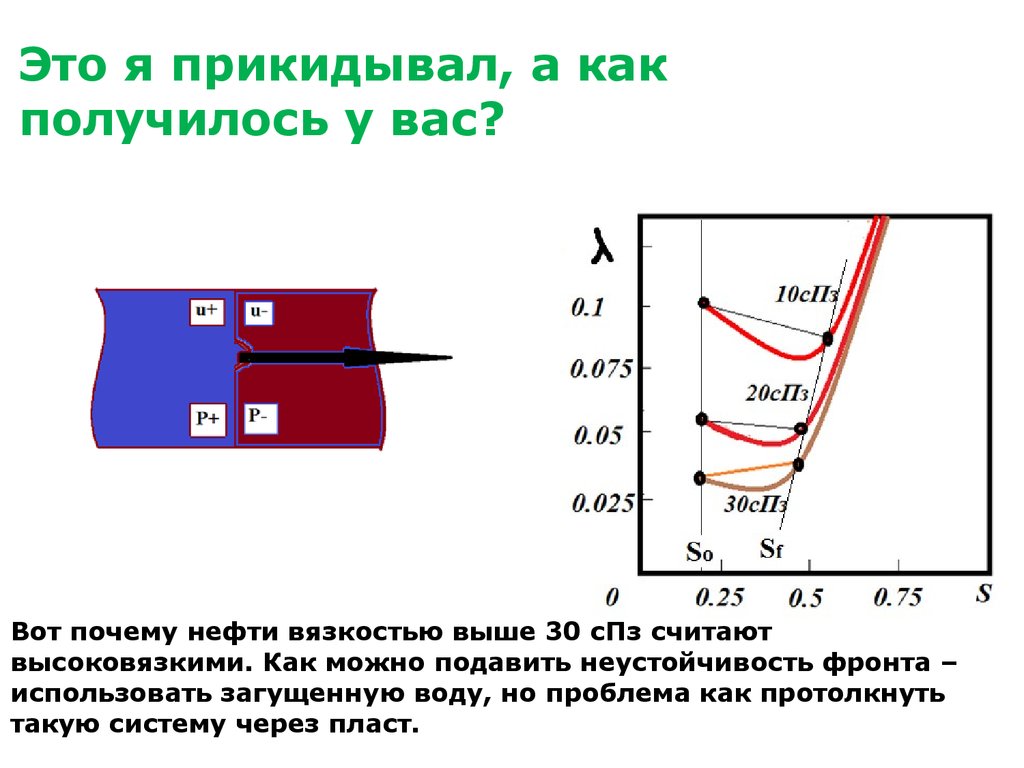
54. Это я прикидывал, а как получилось у вас?
Вот почему нефти вязкостью выше 30 сПз считаютвысоковязкими. Как можно подавить неустойчивость фронта –
использовать загущенную воду, но проблема как протолкнуть
такую систему через пласт.
55. ПРАКТИКА
• Рассчитать соотношение подвижностей М нафронте вытеснения нефти водой для
песчаника и карбонатного пласта, фазовые
проницаемости которых определены в
предыдущих заданиях, а соотношение
вязкостей нефти и воды соответствует 20 и
30.
• Сопоставить условия устойчивости фронта
вытеснения для указанных пластов.
56. Начальное распределение водонасыщенности в пласте
57. Решение
ksNc =
,
oQL k / j
k g
Ng =
oQ
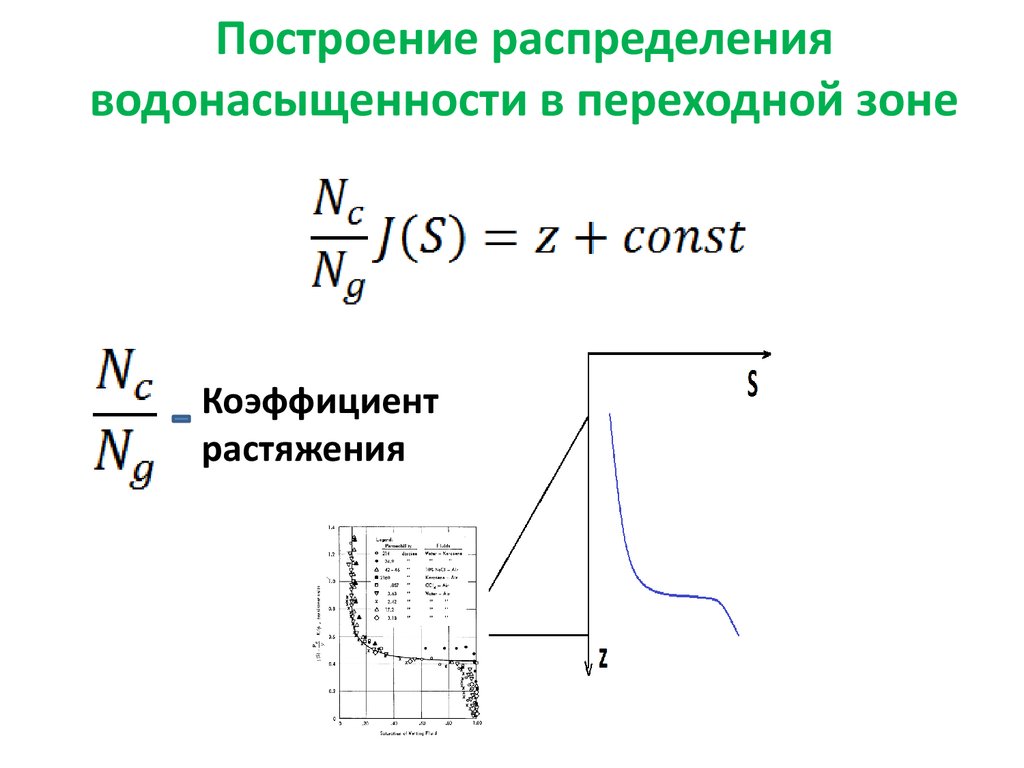
58. Построение распределения водонасыщенности в переходной зоне
Коэффициентрастяжения
59. Масштаб переходной зоны
60. ПРАКТИКА
• Пласт с характеристиками: k = 1, 10 мД,= 0.2,
=200кг/м3, =30мН/м
подстилается водоносным горизонтом.
• Определить размеры переходной зоны для
этих вариантов





























 industry
industry








