Similar presentations:
Acids and Bases
1.
NIS Chem section 12.1CAcids and Bases
2.
NIS Chem section 12.1CVocabulary
Acidity, alkalinity, aqueous
Donor, acceptor
Dissociation
Indicator
2
3.
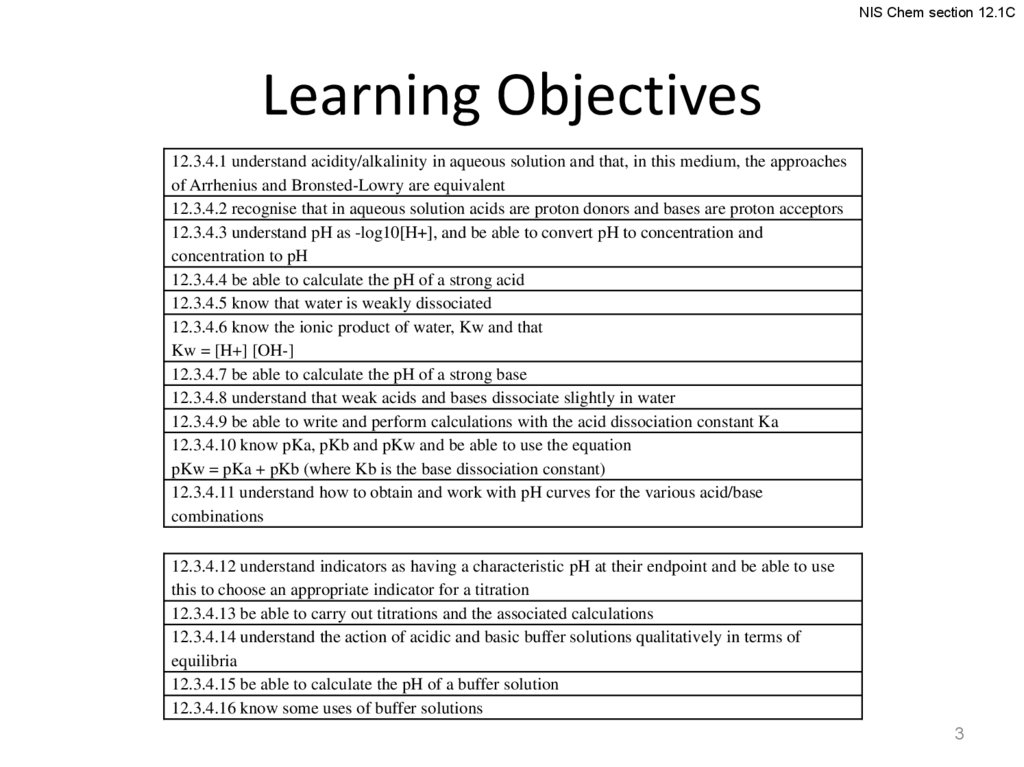
NIS Chem section 12.1CLearning Objectives
12.3.4.1 understand acidity/alkalinity in aqueous solution and that, in this medium, the approaches
of Arrhenius and Bronsted-Lowry are equivalent
12.3.4.2 recognise that in aqueous solution acids are proton donors and bases are proton acceptors
12.3.4.3 understand pH as -log10[H+], and be able to convert pH to concentration and
concentration to pH
12.3.4.4 be able to calculate the pH of a strong acid
12.3.4.5 know that water is weakly dissociated
12.3.4.6 know the ionic product of water, Kw and that
Kw = [H+] [OH-]
12.3.4.7 be able to calculate the pH of a strong base
12.3.4.8 understand that weak acids and bases dissociate slightly in water
12.3.4.9 be able to write and perform calculations with the acid dissociation constant Ka
12.3.4.10 know pKa, pKb and pKw and be able to use the equation
pKw = pKa + pKb (where Kb is the base dissociation constant)
12.3.4.11 understand how to obtain and work with pH curves for the various acid/base
combinations
12.3.4.12 understand indicators as having a characteristic pH at their endpoint and be able to use
this to choose an appropriate indicator for a titration
12.3.4.13 be able to carry out titrations and the associated calculations
12.3.4.14 understand the action of acidic and basic buffer solutions qualitatively in terms of
equilibria
12.3.4.15 be able to calculate the pH of a buffer solution
12.3.4.16 know some uses of buffer solutions
3
4.
NIS Chem section 12.1CAcids and Bases
Arrhenius definition: Classified in terms of formula and
behaviour in water
Acid:
Contains H in formula and produces H+ (or
H3O+) in water. e.g., HCl, H2SO4, HCN, HNO3
Base:
Contains OH in formula and produces OHin water.
e.g., NaOH, Mg(OH)2, KOH
5.
NIS Chem section 12.1CAcids and Bases
Brønsted-Lowry definition: An acid-base reaction is a proton
transfer process
Acid:
Base:
Proton donor during acid-base reaction.
Must contain H in formula.
e.g., NH4+, HCl, H2SO4, HCN, HNO3, HAc
(CH3COOH)
Proton acceptor during acid-base reaction.
Must contain a lone pair of electrons in formula (to
make a bond with H+).
e.g., NH3, Cl-, HSO4-, CN-, NO3-, Ac- (CH3COO-)
6.
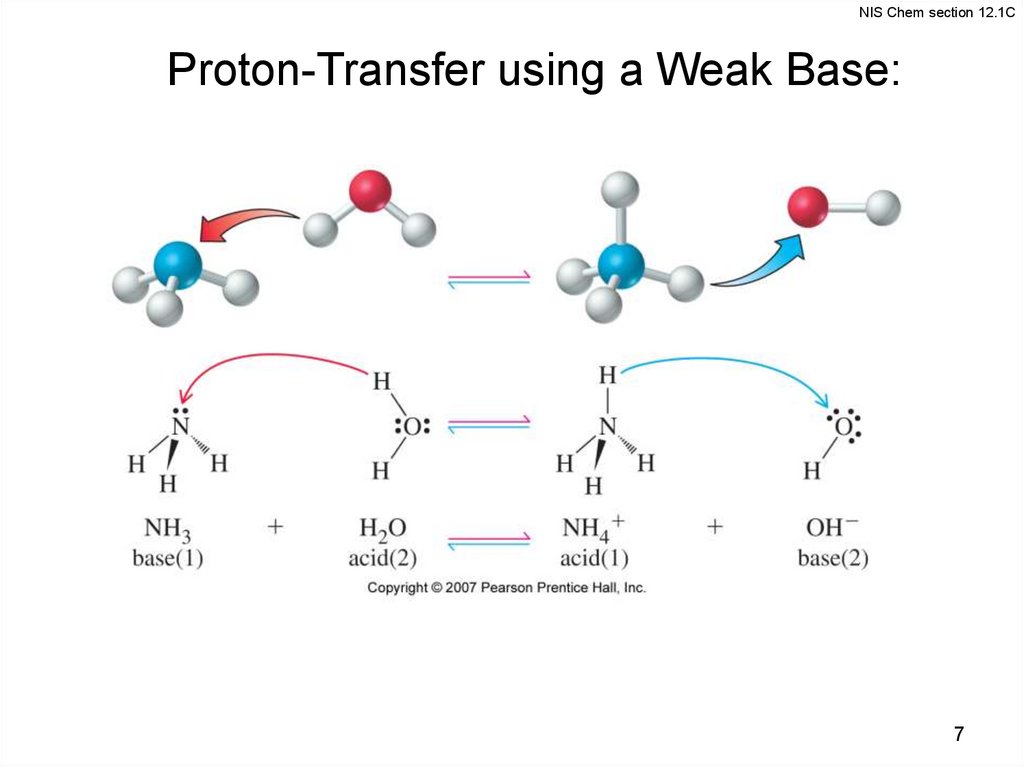
NIS Chem section 12.1CBrønsted-Lowry Acid-Bases
Conjugate acid-base pairs:
NH4+/NH3
HCl/Cl- H2O/OH-
H3O+/H2O
Every acid-base reaction has two conjugate acid-base pairs.
NH4+ is the conjugate acid of NH3:
Is formed when NH3 acts as a base and accepts a proton
NH3 is the conjugate base of NH4+:
Is formed when NH4+ acts as an acid and donates a proton
Amphiprotic (amphoteric):
Can donate or accept protons.
Can act as either acid or base.
e.g., H2O, HSO46
7.
NIS Chem section 12.1CProton-Transfer using a Weak Base:
7
8.
NIS Chem section 12.1CProton-Transfer using a Weak Acid:
8
9.
NIS Chem section 12.1CpH
pH is defined as the negative base-10
logarithm of the hydronium ion concentration.
pH = −log [H3O+]
9
10.
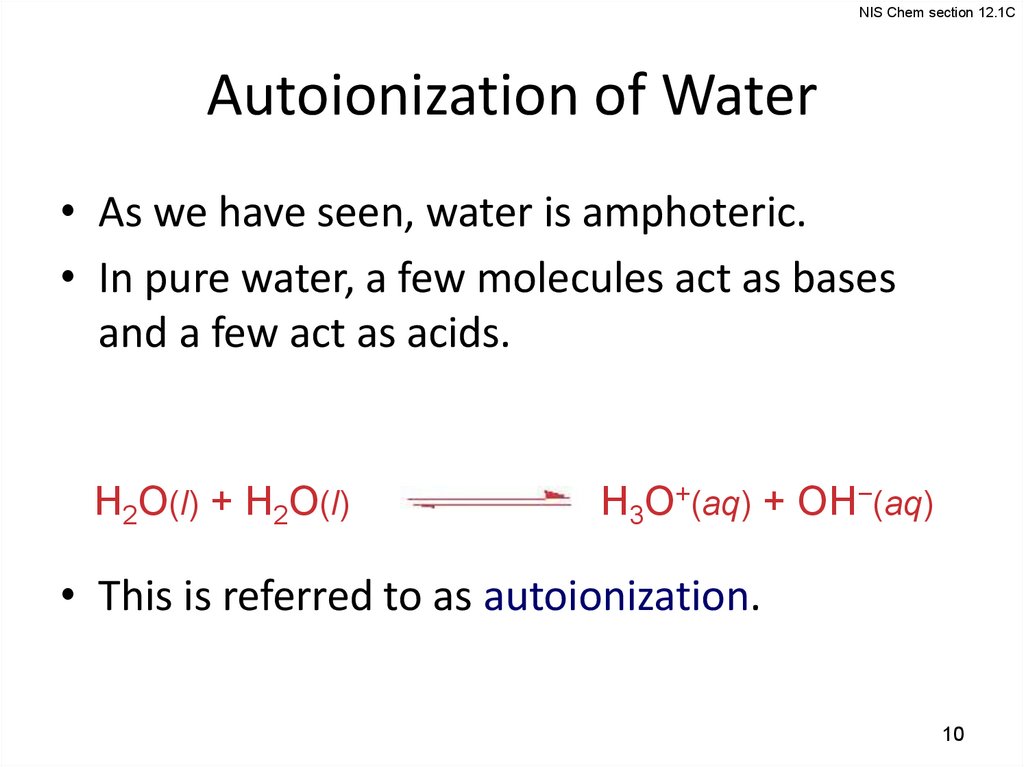
NIS Chem section 12.1CAutoionization of Water
• As we have seen, water is amphoteric.
• In pure water, a few molecules act as bases
and a few act as acids.
H2O(l) + H2O(l)
H3O+(aq) + OH−(aq)
• This is referred to as autoionization.
10
11.
NIS Chem section 12.1CIon-Product Constant
• The equilibrium expression for this process is
Kc = [H3O+] [OH−]
• This special equilibrium constant is referred to
as the ion-product constant for water, Kw.
• At 25 C, Kw = 1.0 10−14
11
12.
NIS Chem section 12.1CpH
• In pure water,
Kw = [H3O+] [OH−] = 1.0 10−14
• Because in pure water [H3O+] = [OH−],
[H3O+] = (1.0 10−14)1/2 = 1.0 10−7
12
13.
NIS Chem section 12.1CpH
• Therefore, in pure water,
pH = −log (1.0 10−7) = 7.00
• An acid has a higher [H3O+] than pure water, so its
pH is <7
• A base has a lower [H3O+] than pure water, so its
pH is >7.
13
14.
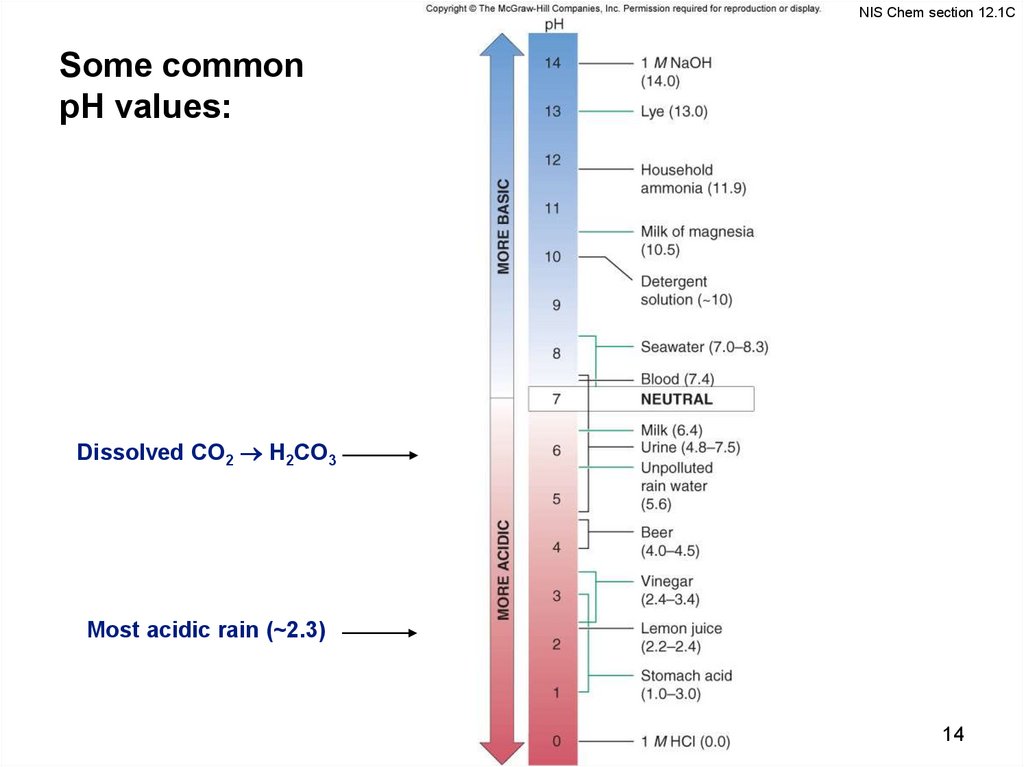
NIS Chem section 12.1CSome common
pH values:
Dissolved CO2 H2CO3
Most acidic rain (~2.3)
14
15.
NIS Chem section 12.1COther “p” Scales
• The “p” in pH tells us to take the negative log
of the quantity (in this case, hydrogen ions).
• Some similar examples are
– pOH −log [OH−]
– pKw −log Kw
15
16.
NIS Chem section 12.1CBecause
[H3O+] [OH−] = Kw = 1.0 10−14,
we know that
−log [H3O+] + −log [OH−] = −log Kw = 14.00
or, in other words,
pH + pOH = pKw = 14.00
16
17.
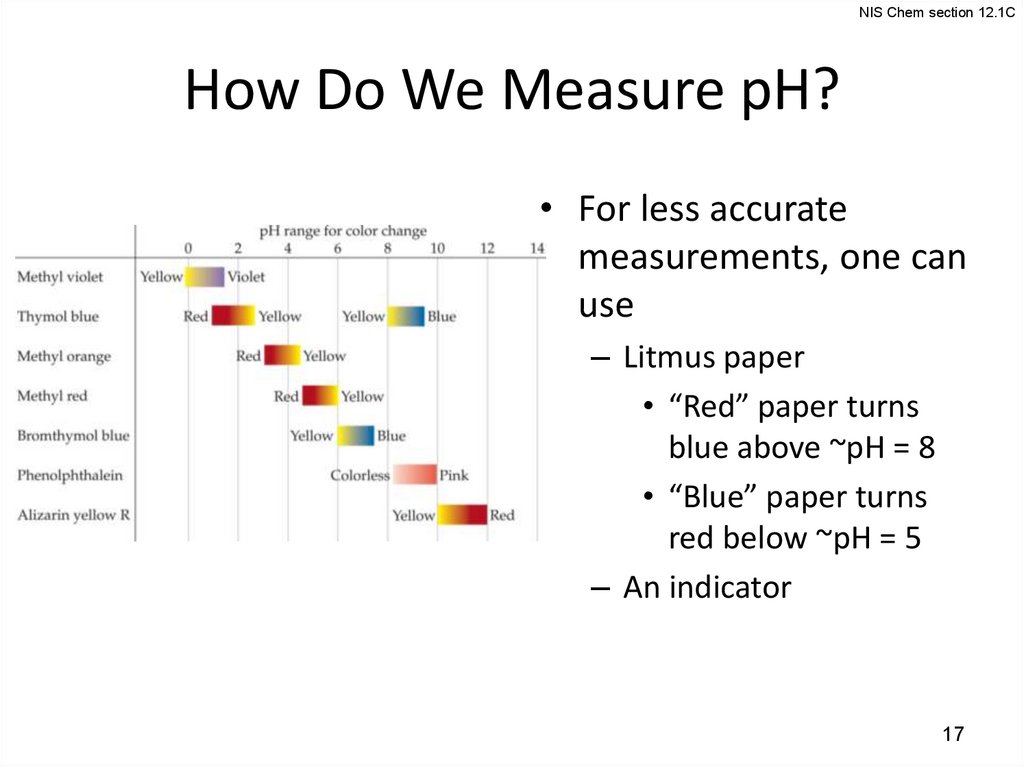
NIS Chem section 12.1CHow Do We Measure pH?
• For less accurate
measurements, one can
use
– Litmus paper
• “Red” paper turns
blue above ~pH = 8
• “Blue” paper turns
red below ~pH = 5
– An indicator
17
18.
NIS Chem section 12.1CHow Do We Measure pH?
For more accurate
measurements, one
uses a pH meter,
which measures the
voltage in the solution.
18
19.
NIS Chem section 12.1CStrong and Weak Acids
What is the difference between a strong and a weak acid?
How much is the equilibrium displaced towards the
formation of the products (ionization)
Strong acid
Strong electrolyte
Close to 100% products
(dissociation)
Weak acid
Weak electrolyte
Very little products
(not much dissociation)
Similar for strong/weak bases
19
20.
NIS Chem section 12.1CStrong Acids
• You will recall that the six strong acids are HCl,
HBr, HI, HNO3, H2SO4 and HClO4.
• These are, by definition, strong electrolytes and
exist totally as ions in aqueous solution.
• For the monoprotic strong acids,
[H3O+] = [acid].
20
21.
NIS Chem section 12.1CStrong Bases
• Strong bases are the soluble hydroxides, which are
the alkali metal and heavier alkaline earth metal
hydroxides (Ca2+, Sr2+, and Ba2+).
• Again, these substances dissociate completely in
aqueous solution.
21
22.
NIS Chem section 12.1CExample problem 1:
a) What is the pH of a 7.52 x 10-4 M CsOH solution?
Is the solution neutral, acidic or basic?
Strong electrolyte, dissociates completely: [OH-] = [CsOH] = 7.52 x 10-4 M
pOH = - log [OH-] = 3.124
pH = 14 – pOH = 10.877
Basic solution
b) What is the pOH of a 1.59 x 10-3 M HClO4 solution?
Is the solution neutral, acidic or basic?
Strong electrolyte, dissociates completely: [H+] = [HClO4] = 1.59 x 10-3 M
pH = - log [H+] = 2.799
Acidic solution
pOH = 14 – pH = 11.201
22
23.
NIS Chem section 12.1CExample problem 2:
a) What is the [H3O+] and [OH-] of a solution with a pH of 2.56?
[H3O+] = 10pH = 10(-2.56) = 2.8 x 10-3
[OH-] = 1.00 x 10-14 / 2.75 x 10-3 = 3.6 x 10-12
b) What is the [H3O+] and [OH-] of a solution with a pOH of 3.78?
[OH-] = 10pOH = 10(-3.78) = 1.7 x 10-4
[H3O+] = 1.00 x 10-14 / 1.66 x 10-4 = 6.0 x 10-11
23
24.
NIS Chem section 12.1CDissociation Constants
• For a generalized acid dissociation,
HA(aq) + H2O(l)
A−(aq) + H3O+(aq)
the equilibrium expression would be
[H3O+] [A−]
Kc =
[HA]
• This equilibrium constant is called the acid
dissociation constant, Ka.
24
25.
NIS Chem section 12.1CDissociation Constants
• For a generalized base dissociation,
B(aq) + H2O(l)
BH+(aq) + OH-(aq)
the equilibrium expression would be
[BH+] [OH−]
Kc =
[B]
• This equilibrium constant is called the base
dissociation constant, Kb.
25
26.
NIS Chem section 12.1CFor the example equation:
CH3COOH ⇌ CH3COO- + H+
CH3COOH is the acid and CH3COO- is its conjugate base.
Combining Ka and Kb gives:
Ka x Kb =
[H+][CH3COO-]
[CH3COOH]
x
[OH-][CH3COOH]
[CH3COO-]
= [H3O+] [OH−] = Kw
=> Kw = Ka ×Kb
=> pKw = pKa + pKb
26
27.
NIS Chem section 12.1CDissociation Constants
The greater the value of Ka, the stronger the
acid.
27
28.
NIS Chem section 12.1CCalculating Ka from the pH
• The pH of a 0.10 M solution of formic acid, HCOOH,
at 25°C is 2.38. Calculate Ka for formic acid at this
temperature.
• We know that
[H3O+] [COO−]
Ka =
[HCOOH]
28
29.
NIS Chem section 12.1CCalculating Ka from the pH
• The pH of a 0.10 M solution of formic acid,
HCOOH, at 25°C is 2.38. Calculate Ka for formic
acid at this temperature.
• To calculate Ka, we need the equilibrium
concentrations of all three components.
• We can find [H3O+], which is the same as [HCOO−],
from the pH.
29
30.
NIS Chem section 12.1CCalculating Ka from the pH
pH = −log [H3O+]
2.38 = −log [H3O+]
−2.38 = log [H3O+]
10−2.38 = 10log [H3O+] = [H3O+]
4.2 10−3 mol/dm3 = [H3O+] = [HCOO−]
[HCOOH] = 0.10 − 4.2 10−3
= 0.0958 = 0.10 mol/dm3
30
31.
NIS Chem section 12.1CCalculating Ka from pH
[4.2 10−3] [4.2 10−3]
Ka =
[0.10]
= 1.8 10−4
31
32.
NIS Chem section 12.1CCalculating pH from Ka
Calculate the pH of a 0.30 M solution of acetic acid,
HC2H3O2, at 25°C.
HC2H3O2(aq) + H2O(l)
H3O+(aq) + C2H3O2−(aq)
Ka for acetic acid at 25°C is 1.8 10−5.
32
33.
NIS Chem section 12.1CCalculating pH from Ka
The equilibrium constant expression is
[H3O+] [C2H3O2−]
Ka =
[HC2H3O2]
33
34.
NIS Chem section 12.1CCalculating pH from Ka
Now,x = [H3O+] = [C2H3O2−]
2
(x)
1.8 10−5 =
(0.30)
(1.8 10−5) (0.30) = x2
5.4 10−6 = x2
2.3 10−3 = x
34
35.
NIS Chem section 12.1CCalculating pH from Ka
pH = −log [H3O+]
pH = −log (2.3 10−3)
pH = 2.64
35
36.
NIS Chem section 12.1CTitration
A known concentration
of base (or acid) is slowly
added to a solution of
acid (or base).
36
37.
NIS Chem section 12.1CTitration
A pH meter or
indicators are used to
determine when the
solution has reached
the equivalence point,
at which the
stoichiometric amount
of acid equals that of
base.
37
38.
METHYL ORANGEacid
end-point
NIS Chem section 12.1C
alkali
39.
PHENOLPHTHALEINacid
alkali
end-point
acid
NIS Chem section 12.1C
alkali
40.
NIS Chem section 12.1CAcid-Base Indicators
• indicate the equivalence point of a titration.
• are weak organic acids for which weak acid and conjugate
base are different colors.
• the color of the solution depends on the ratio of the In- to
the HIn forms:
HIn(aq) + H2O(l)
H3O+(aq) + In- (aq)
• the indicators change color in specific pH ranges close to
the pKa value of the indicator, pKin.
40
41.
NIS Chem section 12.1CAcid-Base Indicators
The sharp change in color of the indicator signals the end
point of the titration.
For the end point of an indicator to be useful,
i.e. indicate the equivalence point accurately:
• it must occur at a volume of titrant very close to that for
the equivalence point of the titration
• the color change of the indicator must be dramatic
enough to be detected.
41
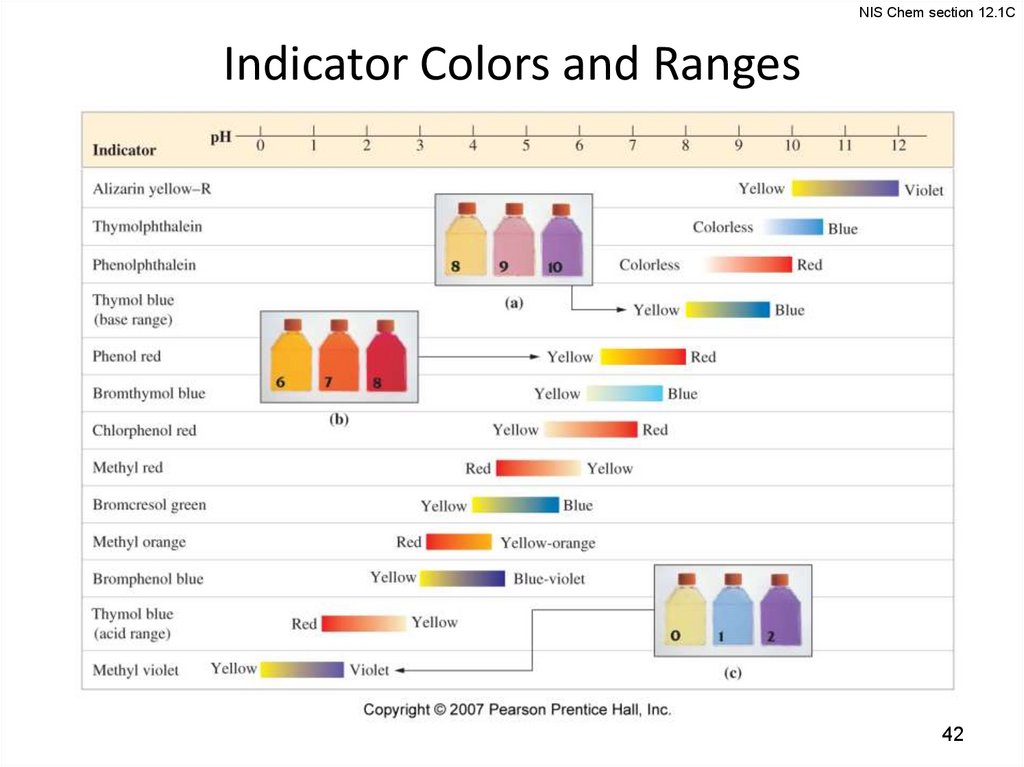
42.
NIS Chem section 12.1CIndicator Colors and Ranges
42
43.
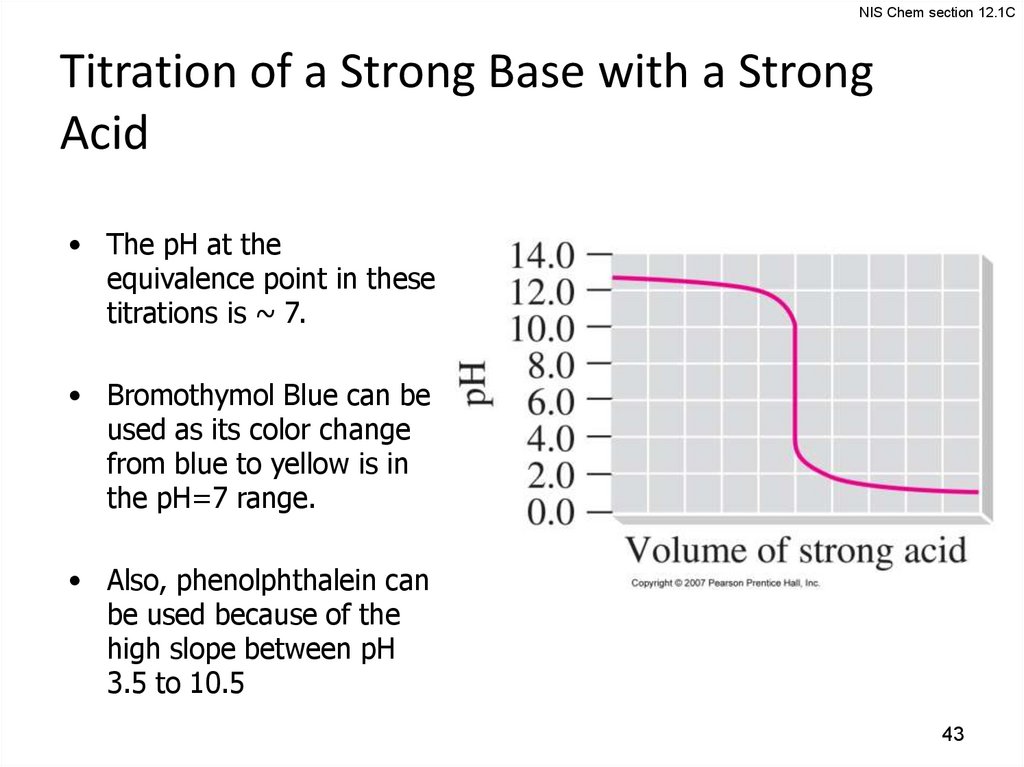
NIS Chem section 12.1CTitration of a Strong Base with a Strong
Acid
• The pH at the
equivalence point in these
titrations is ~ 7.
• Bromothymol Blue can be
used as its color change
from blue to yellow is in
the pH=7 range.
• Also, phenolphthalein can
be used because of the
high slope between pH
3.5 to 10.5
43
44.
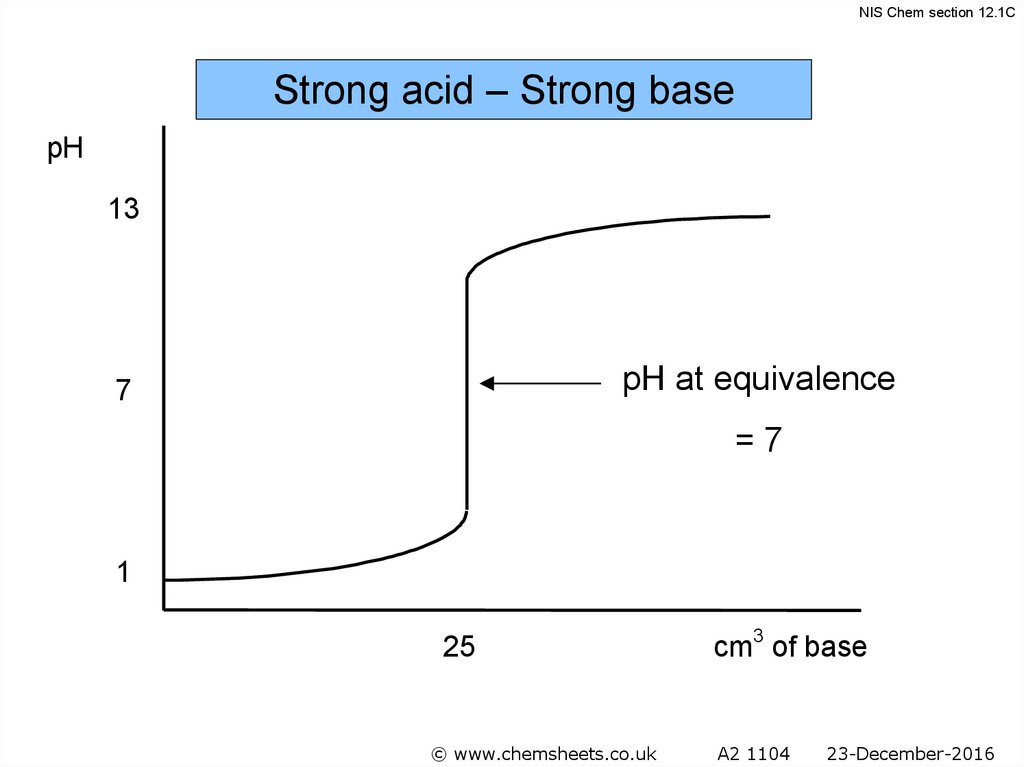
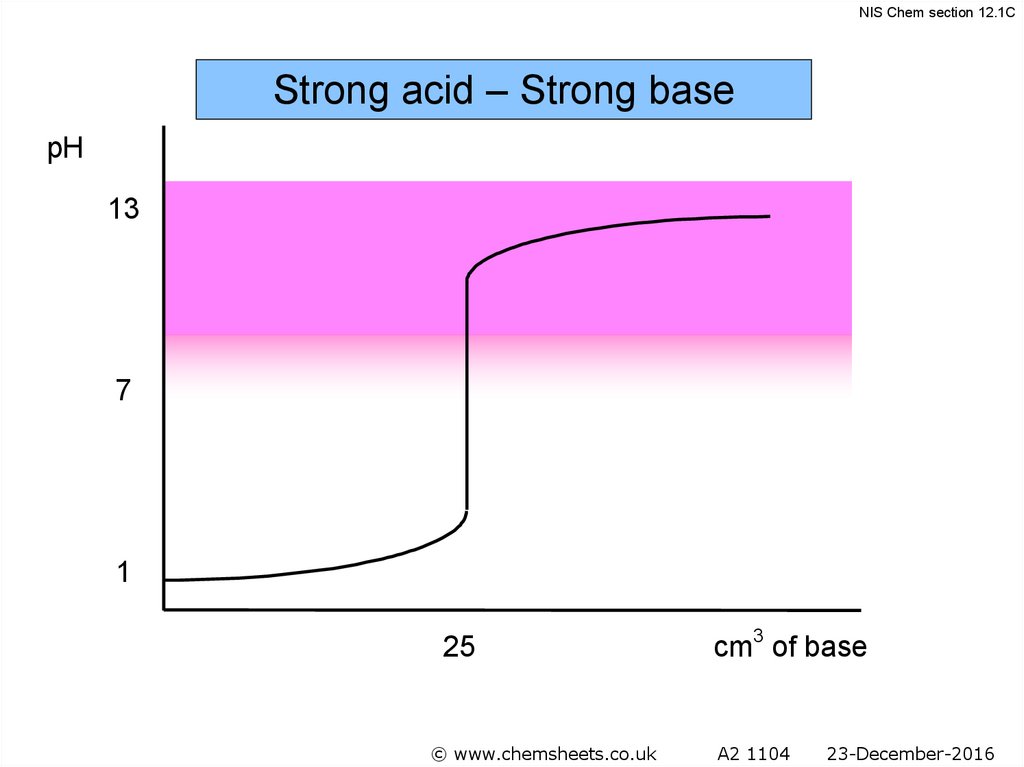
NIS Chem section 12.1CStrong acid – Strong base
pH
13
pH at equivalence
7
=7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
45.
NIS Chem section 12.1CStrong acid – Strong base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
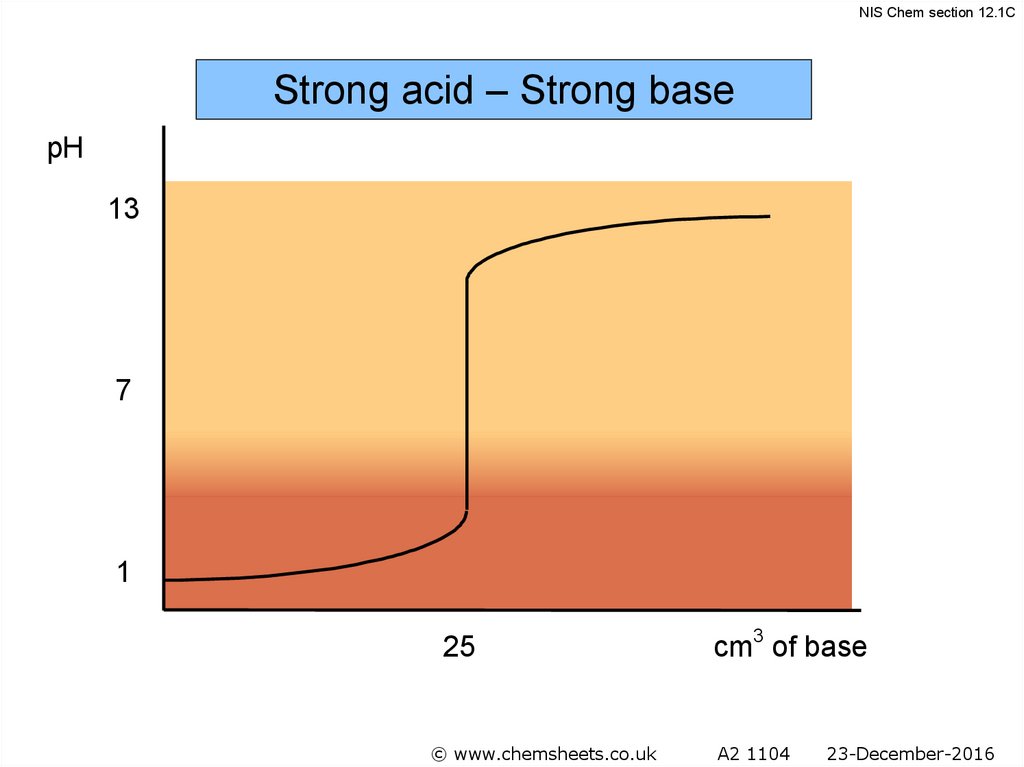
46.
NIS Chem section 12.1CStrong acid – Strong base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
47.
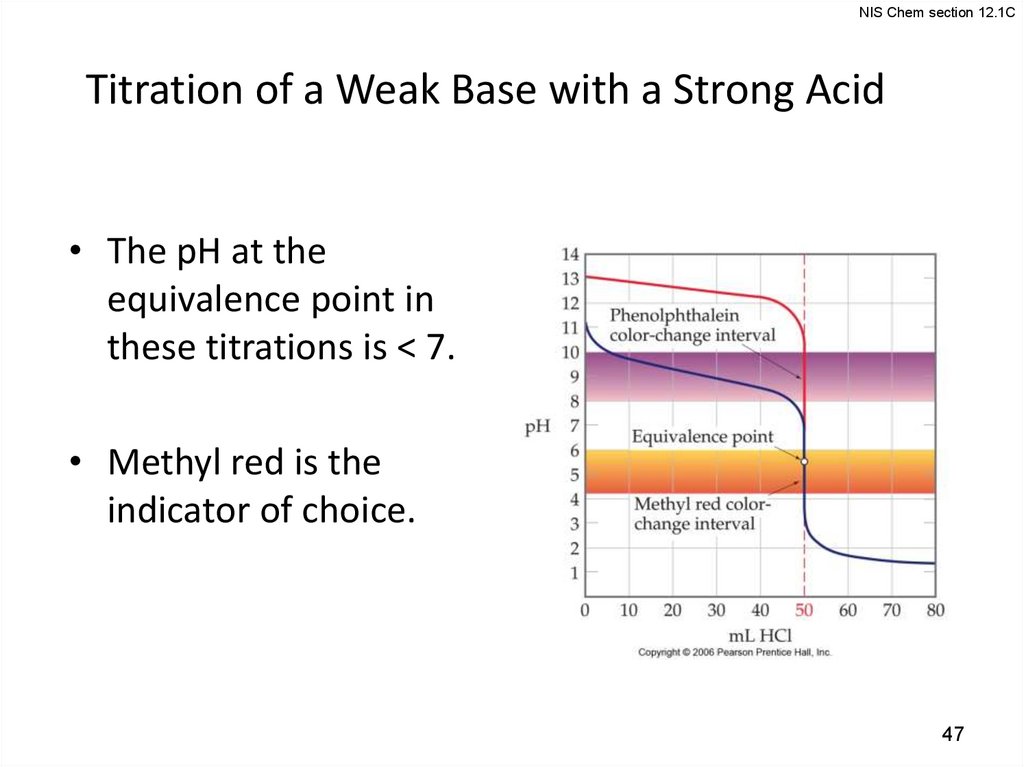
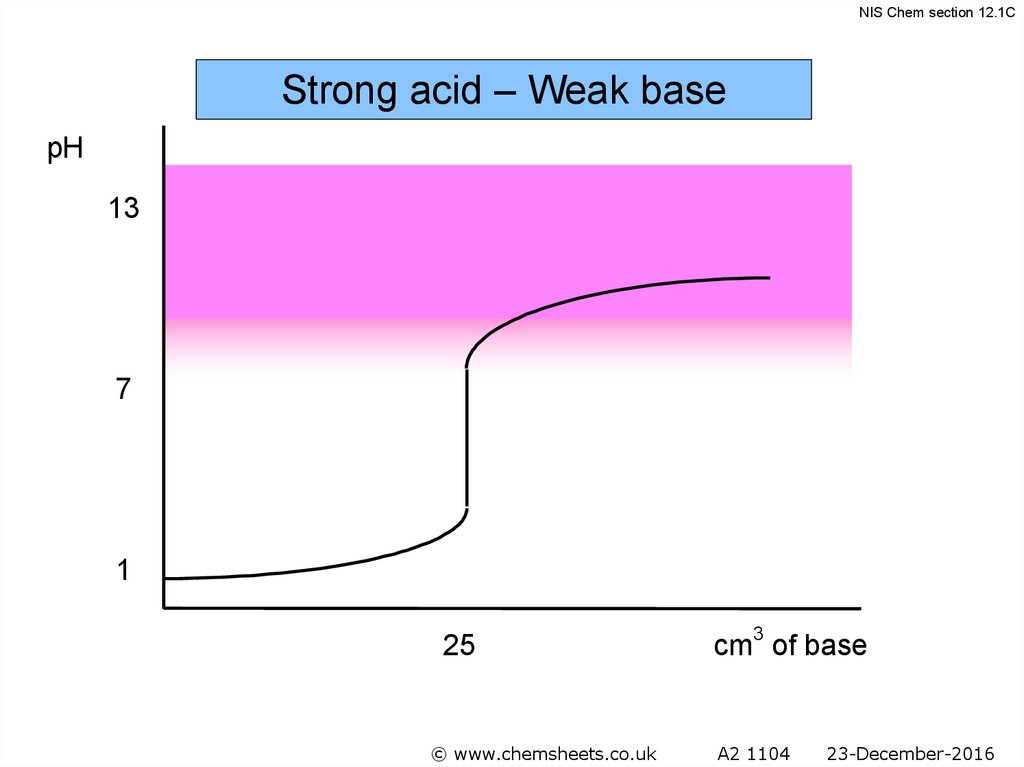
NIS Chem section 12.1CTitration of a Weak Base with a Strong Acid
• The pH at the
equivalence point in
these titrations is < 7.
• Methyl red is the
indicator of choice.
47
48.
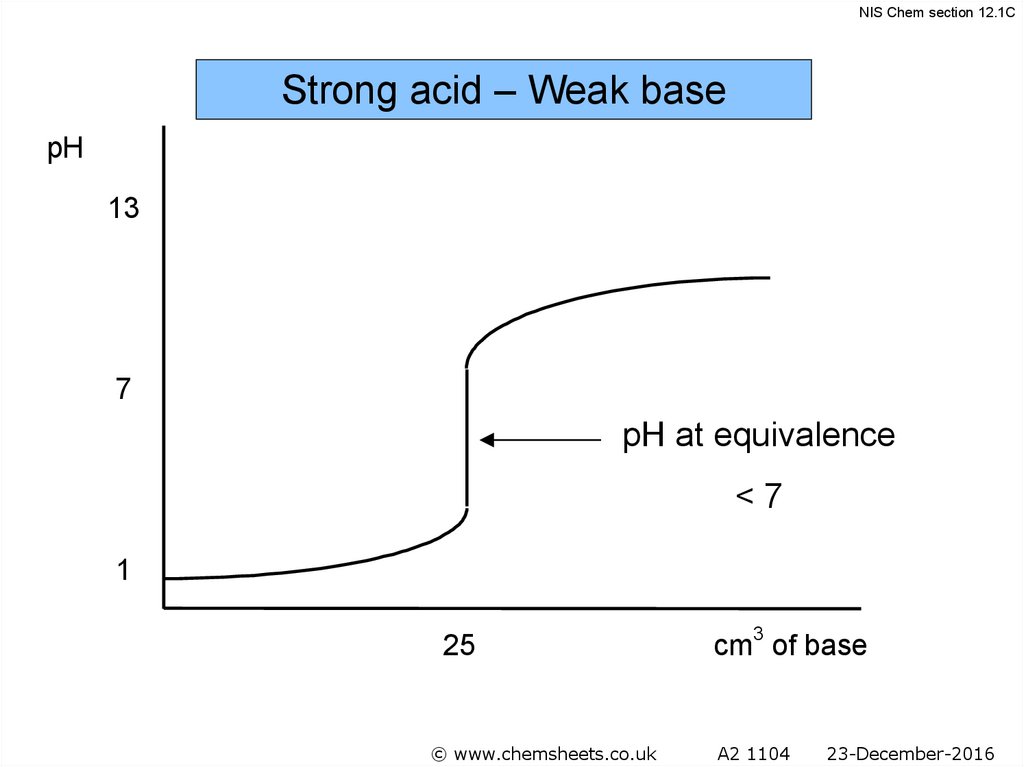
NIS Chem section 12.1CStrong acid – Weak base
pH
13
7
pH at equivalence
<7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
49.
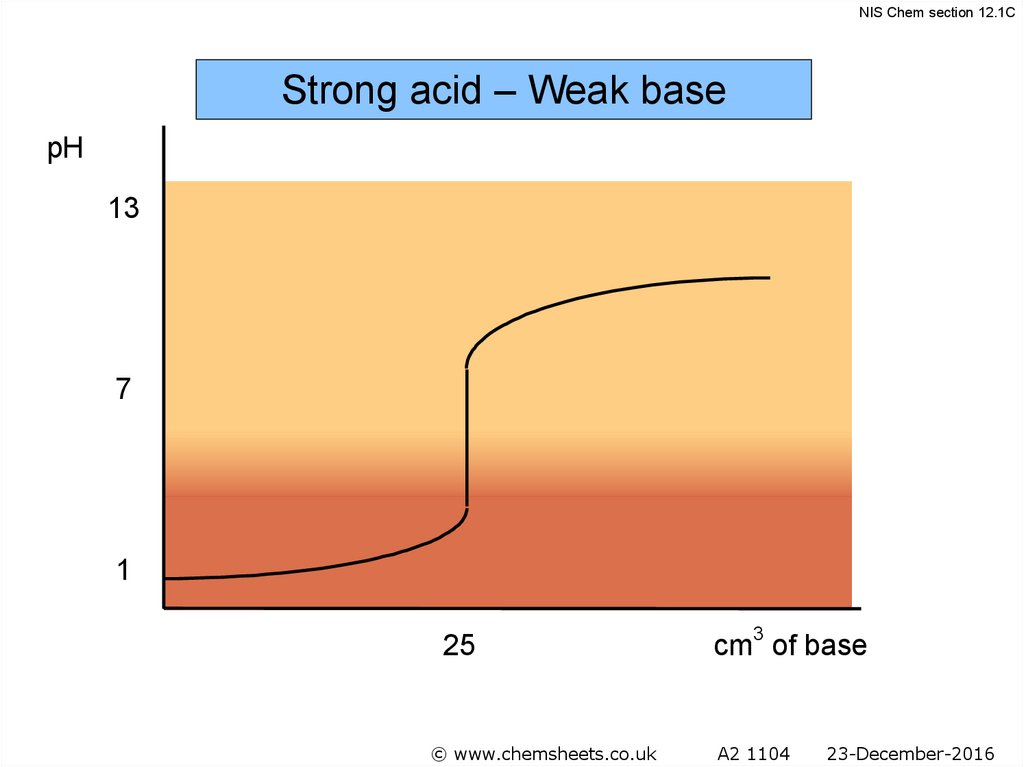
NIS Chem section 12.1CStrong acid – Weak base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
50.
NIS Chem section 12.1CStrong acid – Weak base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
51.
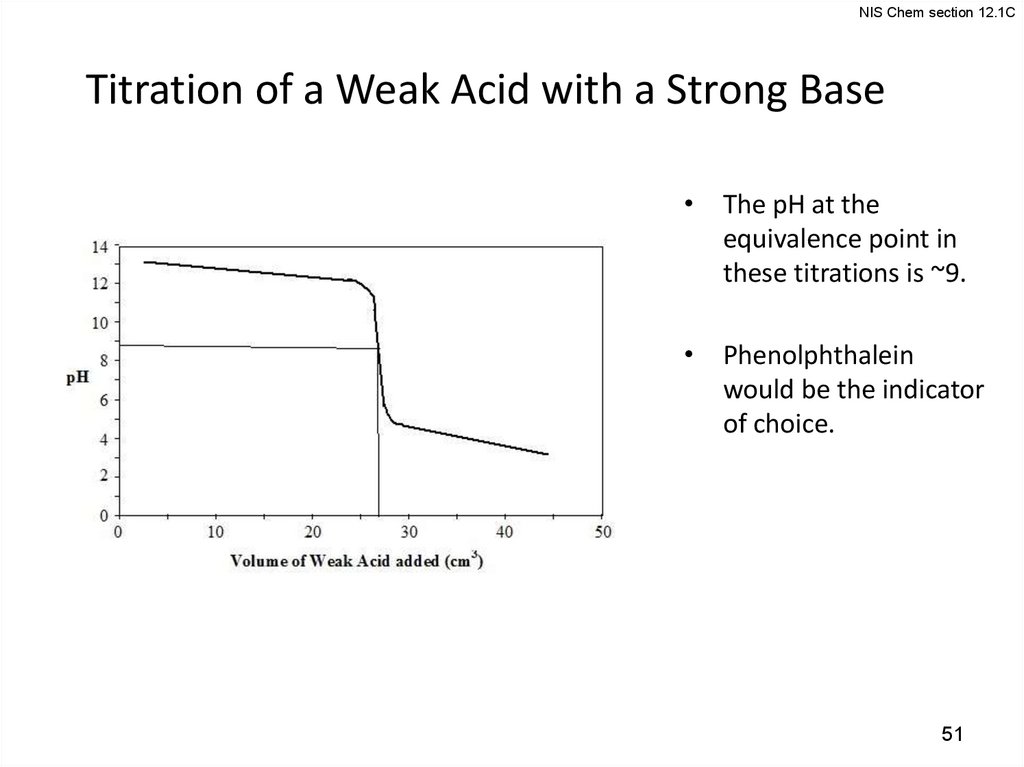
NIS Chem section 12.1CTitration of a Weak Acid with a Strong Base
• The pH at the
equivalence point in
these titrations is ~9.
• Phenolphthalein
would be the indicator
of choice.
51
52.
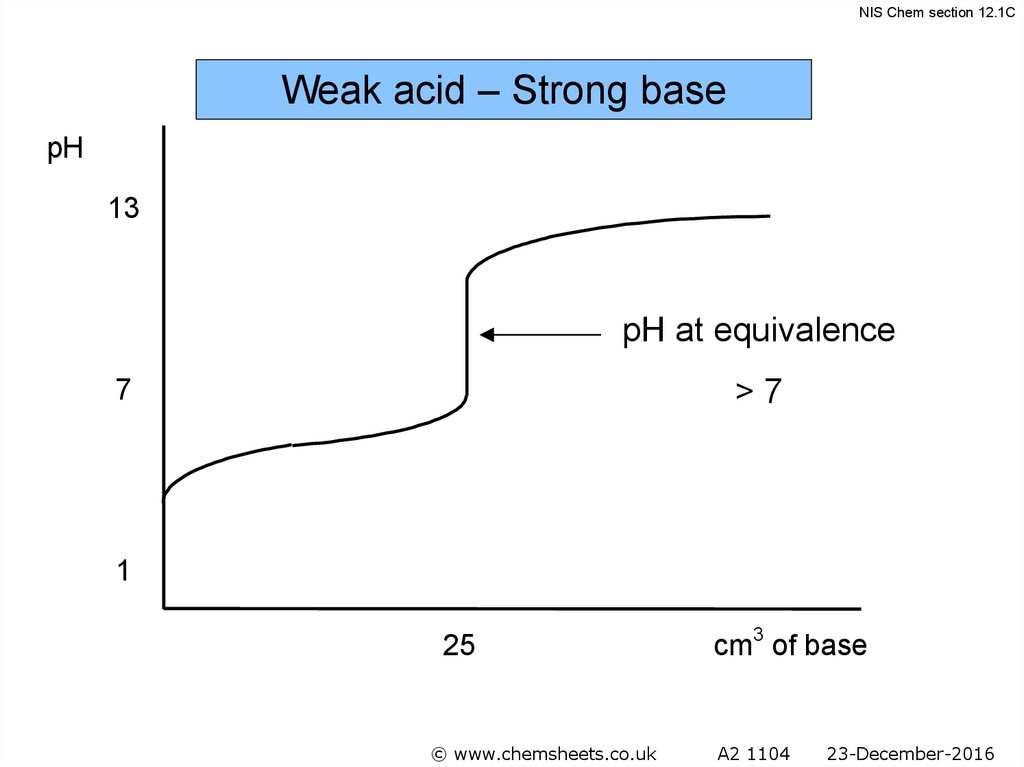
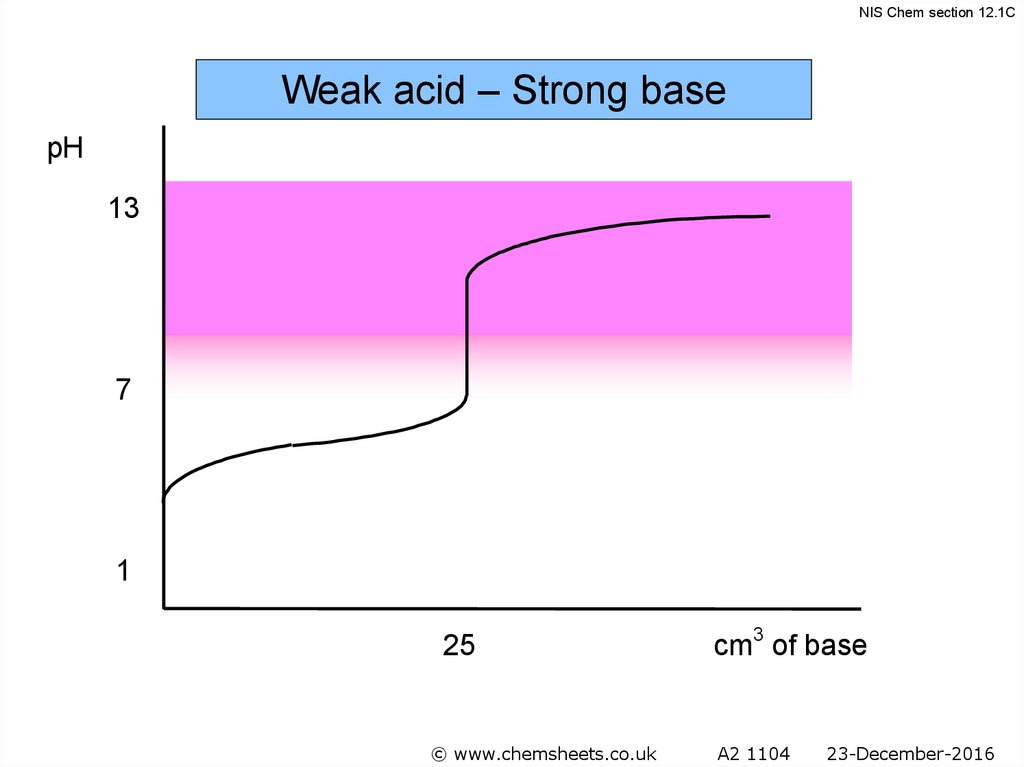
NIS Chem section 12.1CWeak acid – Strong base
pH
13
pH at equivalence
>7
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
53.
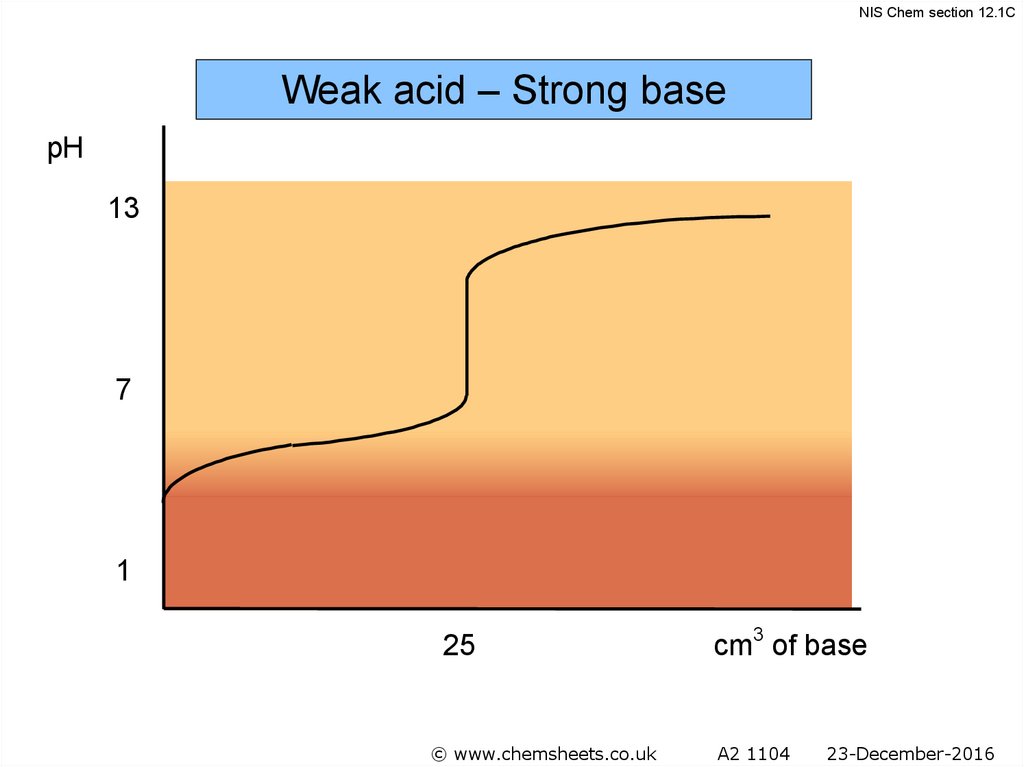
NIS Chem section 12.1CWeak acid – Strong base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
54.
NIS Chem section 12.1CWeak acid – Strong base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
55.
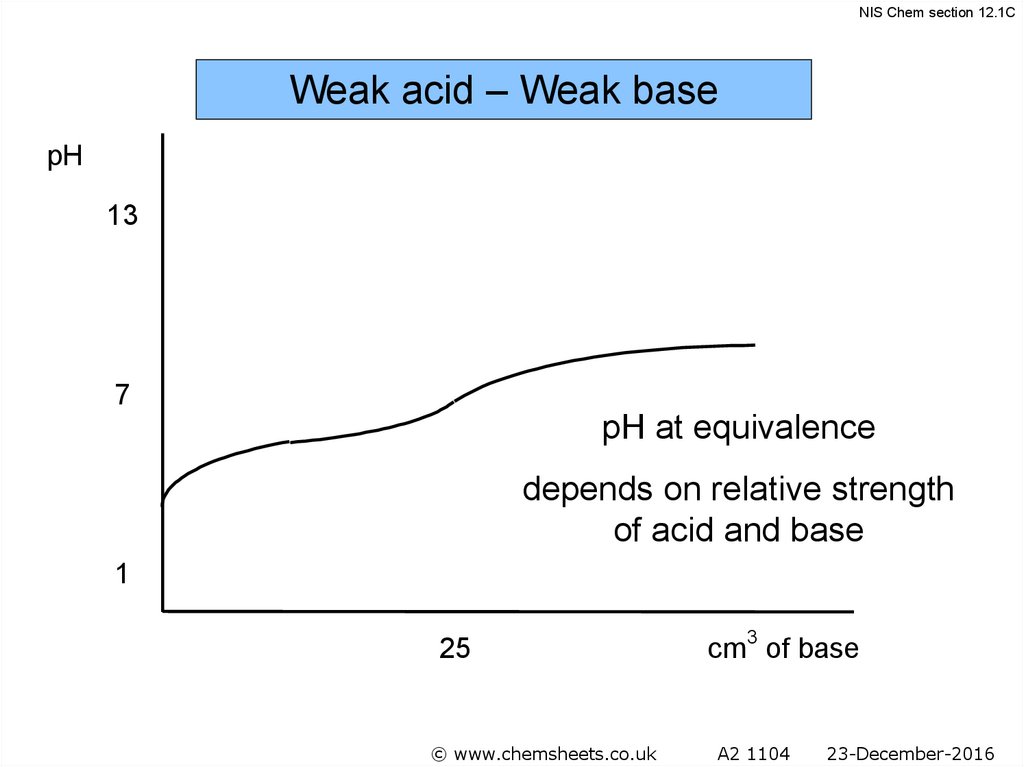
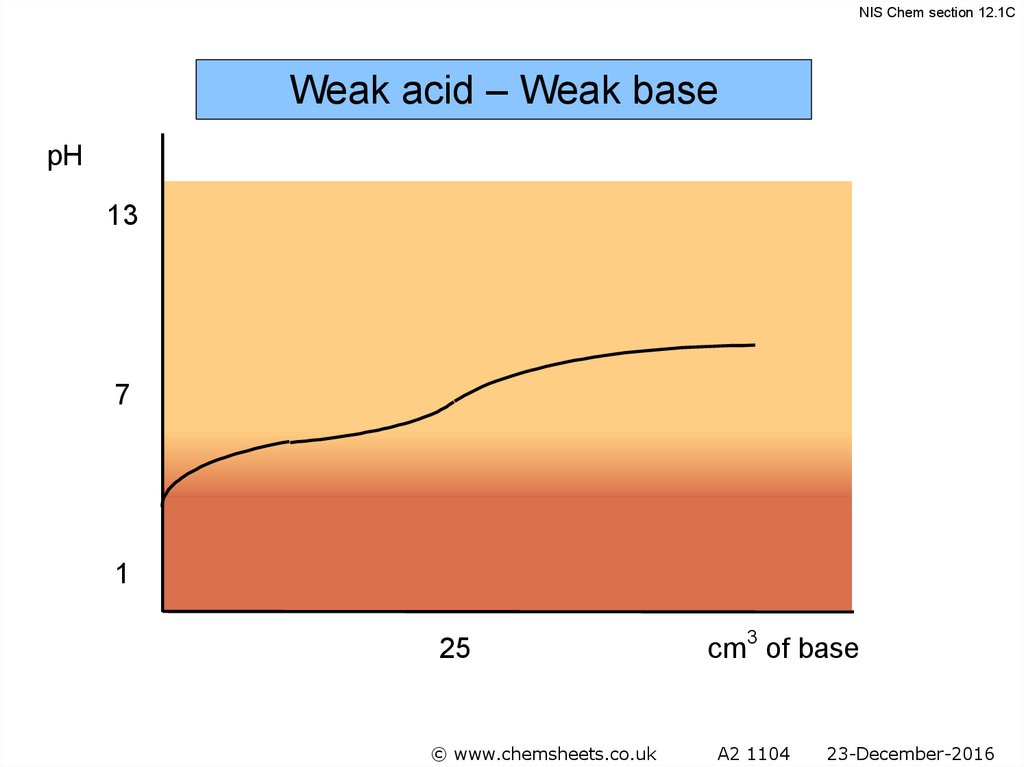
NIS Chem section 12.1CWeak acid – Weak base
pH
13
7
pH at equivalence
depends on relative strength
of acid and base
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
56.
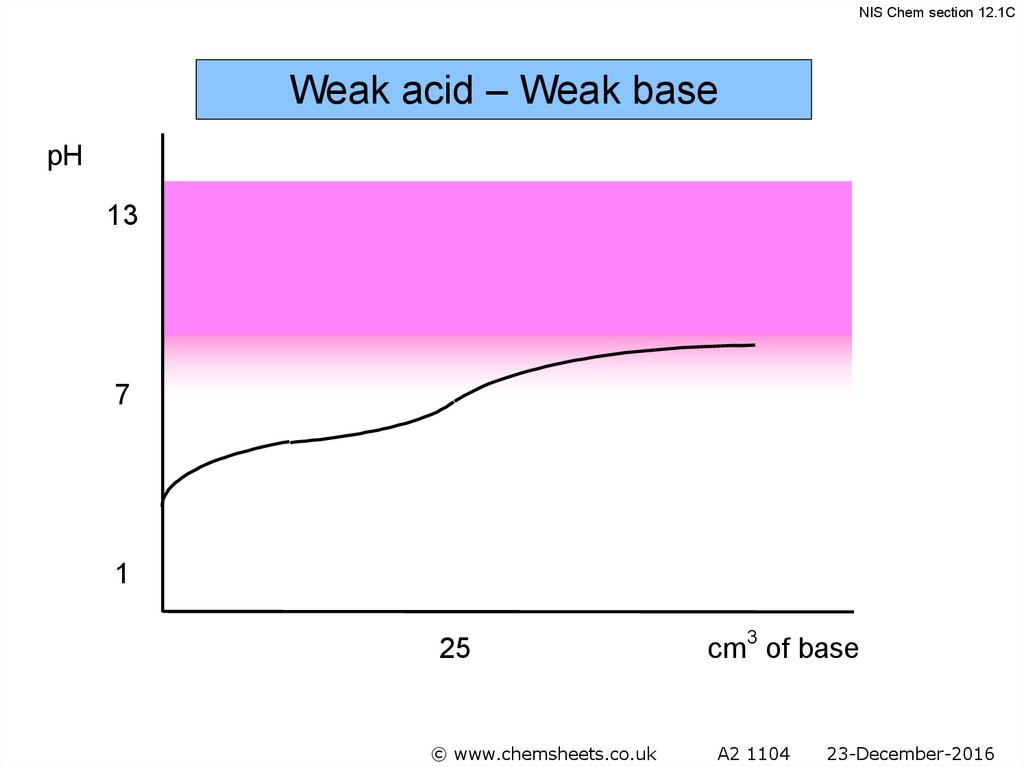
NIS Chem section 12.1CWeak acid – Weak base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
57.
NIS Chem section 12.1CWeak acid – Weak base
pH
13
7
1
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
58.
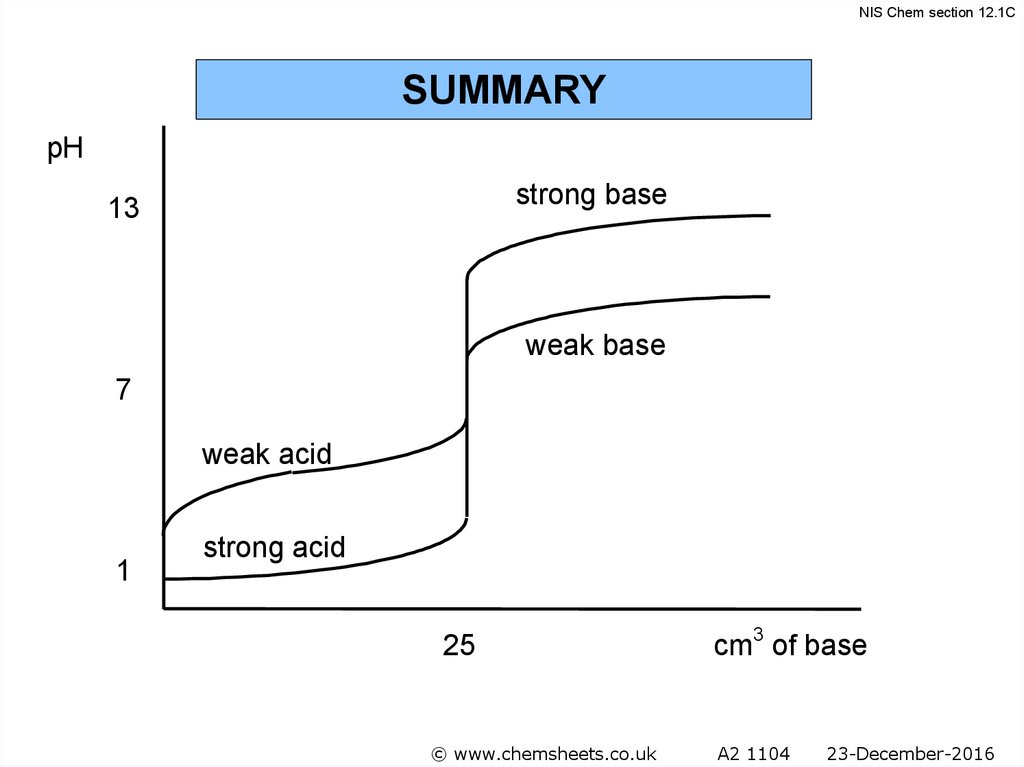
NIS Chem section 12.1CSUMMARY
pH
strong base
13
weak base
7
weak acid
1
strong acid
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
59.
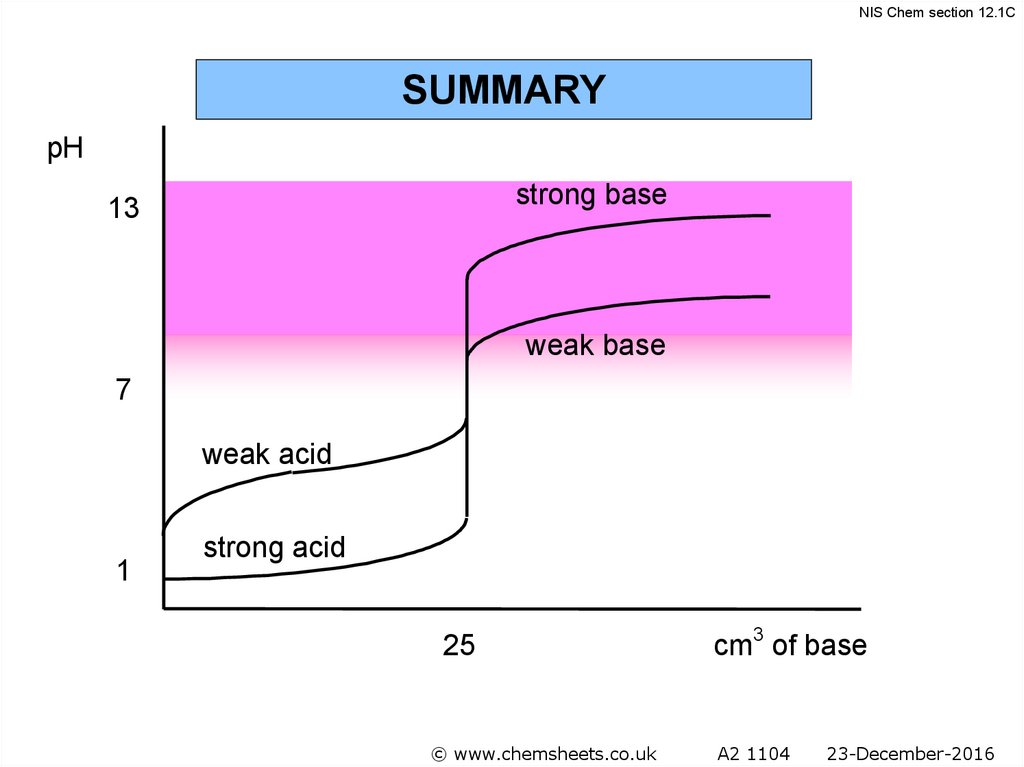
NIS Chem section 12.1CSUMMARY
pH
strong base
13
weak base
7
weak acid
1
strong acid
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
60.
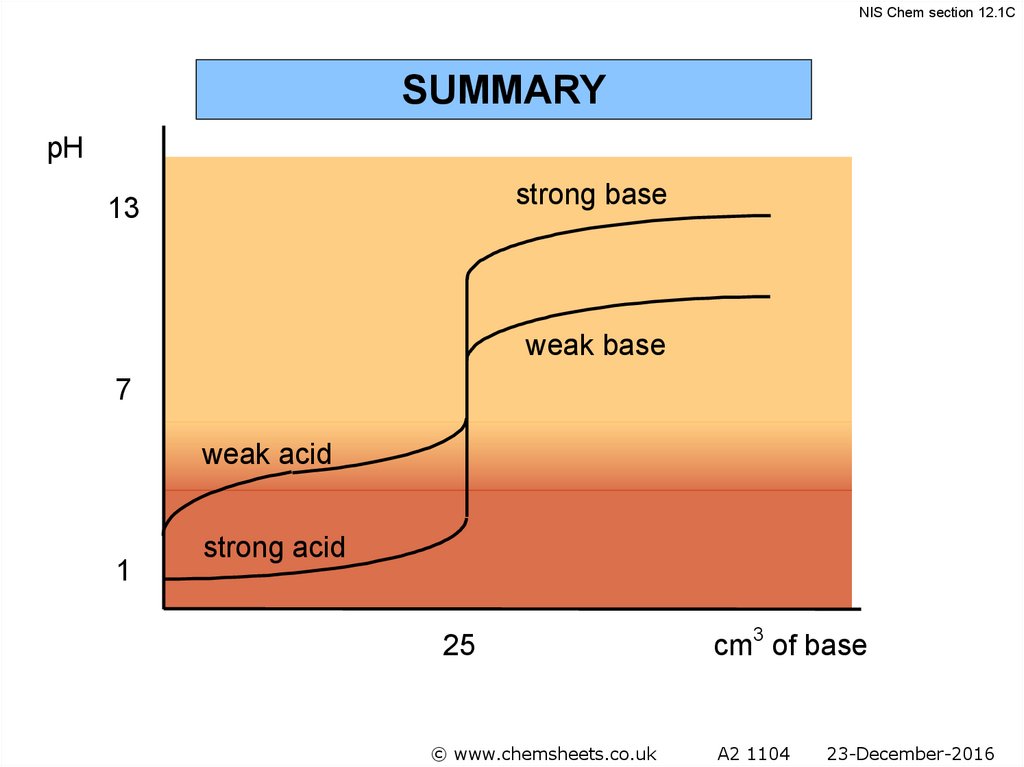
NIS Chem section 12.1CSUMMARY
pH
strong base
13
weak base
7
weak acid
1
strong acid
25
© www.chemsheets.co.uk
cm3 of base
A2 1104
23-December-2016
61.
NIS Chem section 12.1CBuffers:
• Solutions of a weak
conjugate acid-base
pair.
• They are particularly
resistant to pH changes,
even when strong acid
or base is added.
61
62.
NIS Chem section 12.1CBuffers
If a small amount of hydroxide is added to an equimolar
solution of HF in NaF, for example, the HF reacts with the
OH− to make F− and water.
62
63.
NIS Chem section 12.1CBuffers
If acid is added, the F− reacts to form HF and water.
63
64.
NIS Chem section 12.1CBuffer Calculations
Consider the equilibrium constant
expression for the dissociation of a generic
acid, HA:
HA + H2O
H3O+ + A−
[H3O+] [A−]
Ka =
[HA]
64
65.
NIS Chem section 12.1CBuffer Calculations
Rearranging slightly, this becomes
−]
[A
Ka = [H3O+]
[HA]
Taking the negative log of both side, we get
−]
[A
−log Ka = −log [H3O+] + −log
[HA]
pKa
pH
base
acid
65
66.
NIS Chem section 12.1CBuffer Calculations
• So
[base]
pKa = pH − log
[acid]
• Rearranging, this becomes
[base]
pH = pKa + log
[acid]
• This is the Henderson–Hasselbalch equation.
66
67.
NIS Chem section 12.1CHenderson–Hasselbalch Equation
What is the pH of a buffer that is 0.12 M in
lactic acid, HC3H5O3, and 0.10 M in sodium
lactate? Ka for lactic acid is
1.4 10−4.
67
68.
NIS Chem section 12.1CHenderson–Hasselbalch Equation
[base]
pH = pKa + log
[acid]
pH = −log (1.4
10−4)
(0.10)
+ log (0.12)
pH = 3.85 + (−0.08)
pH = 3.77
68
69.
NIS Chem section 12.1CBuffer Uses
• Electroplating
• Manufacture of Dyes
• Calibrating pH meters
• Buffering blood using combinations of:
HCO3- ; hemoglobin ; H2PO4- ; HPO4269
70.
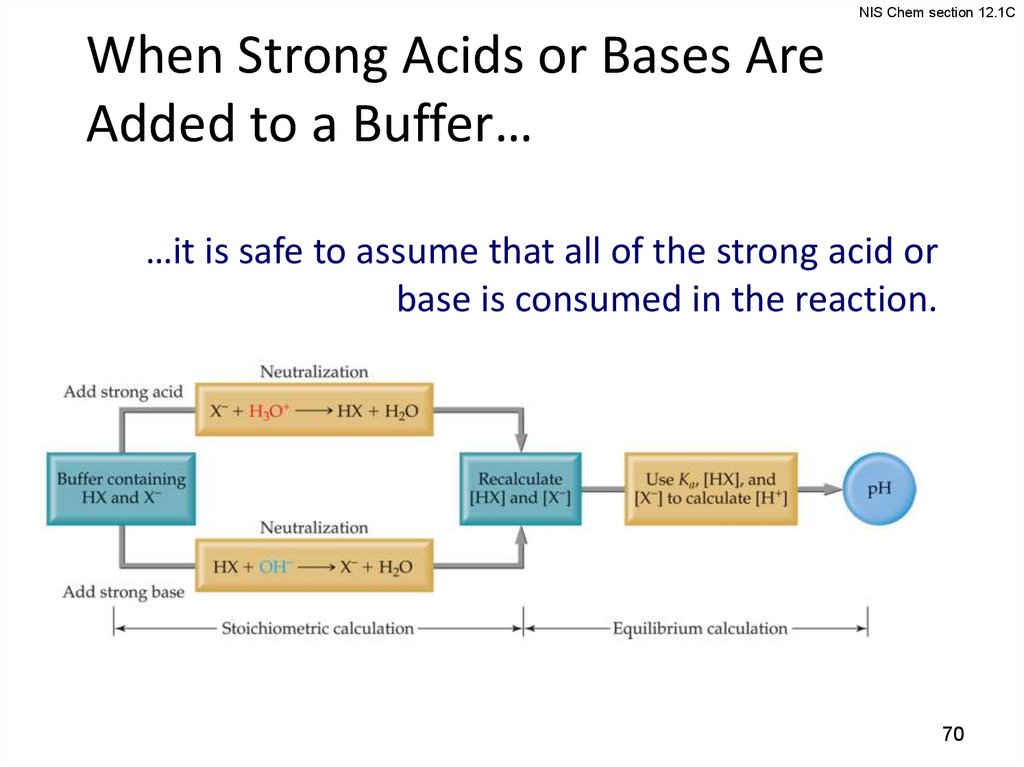
NIS Chem section 12.1CWhen Strong Acids or Bases Are
Added to a Buffer…
…it is safe to assume that all of the strong acid or
base is consumed in the reaction.
70
71.
NIS Chem section 12.1CAddition of Strong Acid or Base to a
Buffer
1. Determine how the neutralization
reaction affects the amounts of the
weak acid and its conjugate base in
solution.
2. Use the Henderson–Hasselbalch
equation to determine the new pH
of the solution.
71
72.
NIS Chem section 12.1CCalculating pH Changes in Buffers
A buffer is made by adding 0.300 mol HC2H3O2 and 0.300
mol NaC2H3O2 to enough water to make 1.00 L of solution.
The pH of the buffer is 4.74. Calculate the pH of this
solution after 0.020 mol of NaOH is added.
Before the reaction, since
n (CH3COOH) = n (CH3COO−)
pH = pKa = −log (1.8 10−5) = 4.74
72
73.
NIS Chem section 12.1CCalculating pH Changes in Buffers
The 0.020 mol NaOH will react with 0.020 mol of the
acetic acid:
CH3COOH(aq) + OH−(aq) CH3COO−(aq) + H2O(l)
CH3COOH CH3COO−
OH−
Before reaction
0.300 mol
0.300 mol 0.020 mol
After reaction
0.280 mol
0.320 mol 0.000 mol
73
74.
NIS Chem section 12.1CCalculating pH Changes in Buffers
Now use the Henderson–Hasselbalch equation to
calculate the new pH:
(0.320)
pH = 4.74 + log
(0. 280)
pH = 4.74 + 0.06
pH = 4.80
74

















































 chemistry
chemistry








