Балочная теория тонкостенных конструкций

1.

Глушков Сергей Валериевич
к.т.н., доцент кафедры космического машиностроения

2.

Рассчитать
нормальные
в тонкостенной конструкции
a
и
касательные
a 200мм
1
2
F1
b 250мм
r
r 300мм
h 400мм
F2
F2
3
Qy
h
h
2
F1
b
напряжения
1 2,5мм
2 2мм
3 3мм
F1 350мм 2
F2 250мм 2
Eоб 7 104 МПа
Eп 2,05 105 МПа
В сечении действуют
M x 80кН м
Qy 30 кН
2

3.

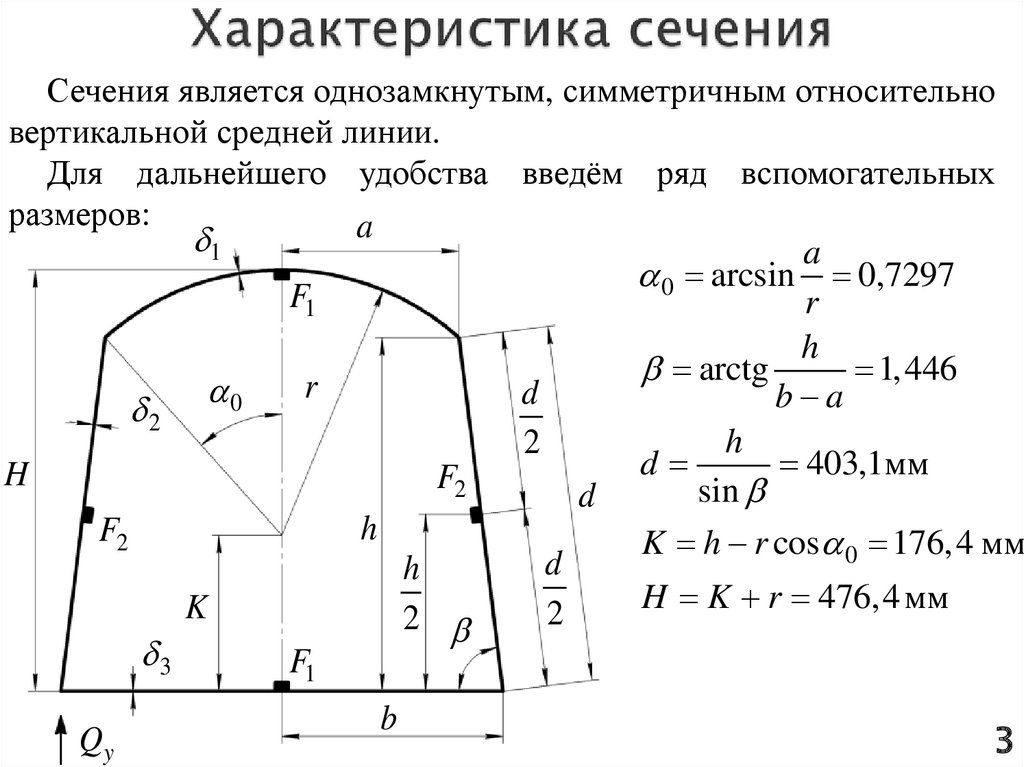
Сечения является однозамкнутым, симметричным относительно
вертикальной средней линии.
Для дальнейшего удобства введём ряд вспомогательных
размеров:
a
1
a
0 arcsin 0,7297
F1
r
h
arctg
1,446
r
0
d
b a
2
h
2
d
403,1мм
H
F2
sin
d
h
F2
K h r cos 0 176,4 мм
d
h
H K r 476,4мм
K
2
2
3
F1
Qy
b
3

4.

Обшивка изготовлена из материала, модуль упругости которого
существенно ниже, чем модуль упругости материала поясов.
Целесообразно привести материал поясов к материалу обшивки, это
позволит в дальнейшем оперировать коэффициентом приведения
(редукции) большим единицы.
Примечание:
редукционный
коэффициент
больше
единицы
показывает, во сколько раз нужно увеличить площадь пояса, если бы они
были изготовлены из материала обшивки. Приведение обшивки к
материалу поясов менее наглядно, поскольку получаемый коэффициент
существенно меньше единицы и говорит о необходимости тонкую
обшивку еще уменьшить толщину при изготовлении из более жесткого
материала.
об
Eоб
1
Eоб
Eп 2,05 105
п
2,93
4
Eоб
7 10
4

5.

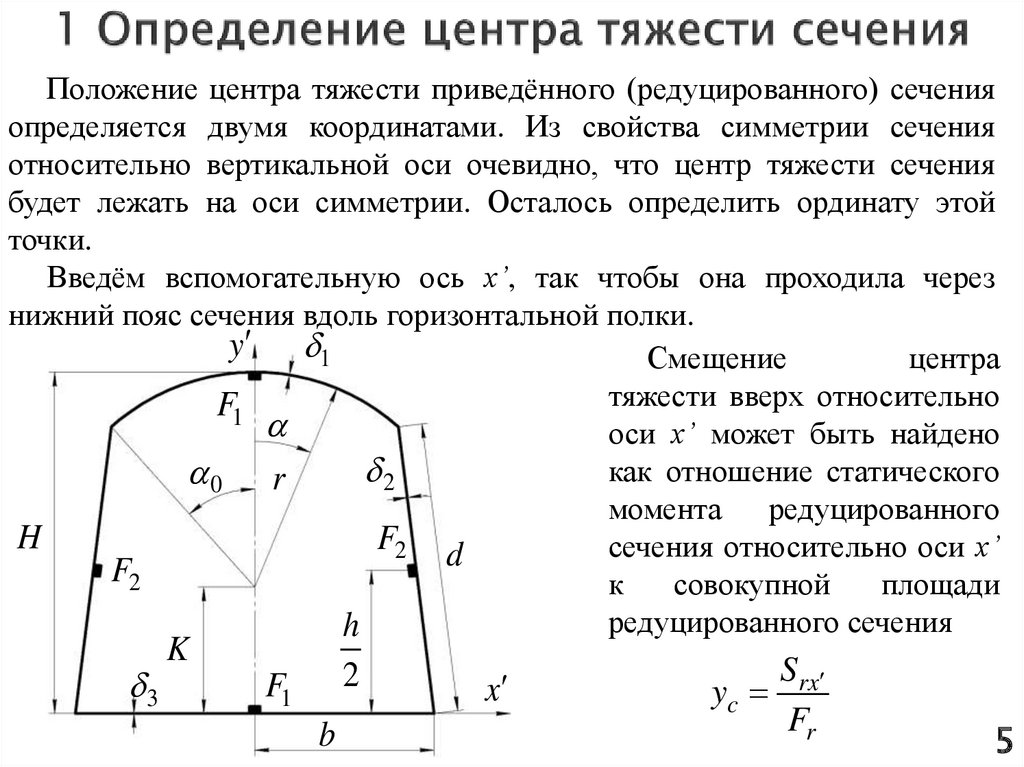
Положение центра тяжести приведённого (редуцированного) сечения
определяется двумя координатами. Из свойства симметрии сечения
относительно вертикальной оси очевидно, что центр тяжести сечения
будет лежать на оси симметрии. Осталось определить ординату этой
точки.
Введём вспомогательную ось x’, так чтобы она проходила через
нижний пояс сечения вдоль горизонтальной полки.
y 1
Смещение
центра
тяжести вверх относительно
F1
оси x’ может быть найдено
2
как отношение статического
0 r
момента редуцированного
H
F2 d
сечения относительно оси x’
F2
к
совокупной
площади
редуцированного сечения
h
3
K
2
F1
b
x
Srx
yc
Fr
5

6.

y
F1
0
1
r
2
H
F2
F2
3
h
2
K
F1
d
x
Площадь редуцированного
сечения
складывается
из
площадей участков обшивки
(как
произведение
длины
участка на его толщину) и
суммы
площадей
поясов,
умноженных на редукционный
коэффициент
b
Fr об 0 r 1 d 2 b 3 2 п F1 2 F2 F1
1 0,7297 300 2,5 403,1 2 250 3 2
2,93 350 2 250 350 7721 мм 2
6

7.

y
F1
0
1
r
2
H
F2
F2
3
h
2
K
F1
d
x
Статические
момент
редуцированного
сечения
складывается из произведения
площадей отдельных участков
обшивки (длина участка на его
толщину)
на
расстояние
до
выбранной оси и суммы площадей
поясов,
умноженных
на
редукционный коэффициент и на
расстояние до выбранной оси
b
0
h
h
S rx об K r cos 1 rd d 2 2 п F1H 2 F2
2
2
0
ds
h
h
об K 1r 0 r 2 1 sin 0 d 2 2 п F1H 2 F2
2
2
400
1 176,4 2,5 300 0,7297+300 2 2,5 sin 0,7297 403,1 2
2
400
3
2,93 350 476,4 2 250
1596729 мм
2
7

8.

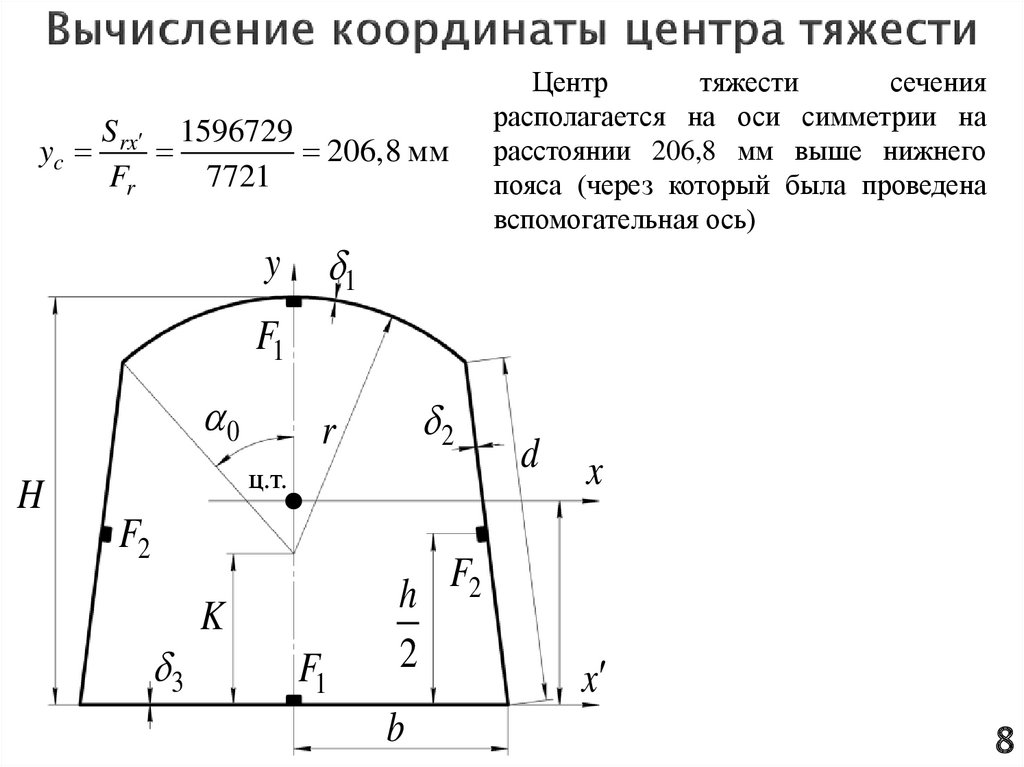
yc
Srx 1596729
206,8 мм
Fr
7721
y
Центр
тяжести
сечения
располагается на оси симметрии на
расстоянии 206,8 мм выше нижнего
пояса (через который была проведена
вспомогательная ось)
1
F1
0
2
r
ц.т.
H
F2
3
K
F1
F
h 2
2
b
d
x
x
8

9.

При определение центра тяжести сечения ответственным шагом
является выбор вспомогательной оси, относительно который
вычисляется статический момент редуцированного сечения.
Здесь следует учитывать тот факт, что статический момент элемента
сечения, располагающегося соосно, или пояса, лежащего на
вспомогательной оси, относительно этой оси – равен нулю.
Поэтому, хотя выбор вспомогательной оси является произвольным,
целесообразно ось проводить через один из конструктивных элементов
сечения, чтобы упростить формулы расчёта.
При подсчете статического момента криволинейных участков –
разумно перейти от дуговой координаты, отсчитываемой вдоль линии
контура, к угловому параметру.
При возможности удобно проводить вспомогательную ось через
крайнюю точку сечения так, чтобы все сечение лежало выше или ниже
этой оси. Это позволит автоматически принимать все координаты
(расстояния от элемента площади до оси) одного знака, и такого же знака
будет результат – расстояние до центра тяжести.
9

10.

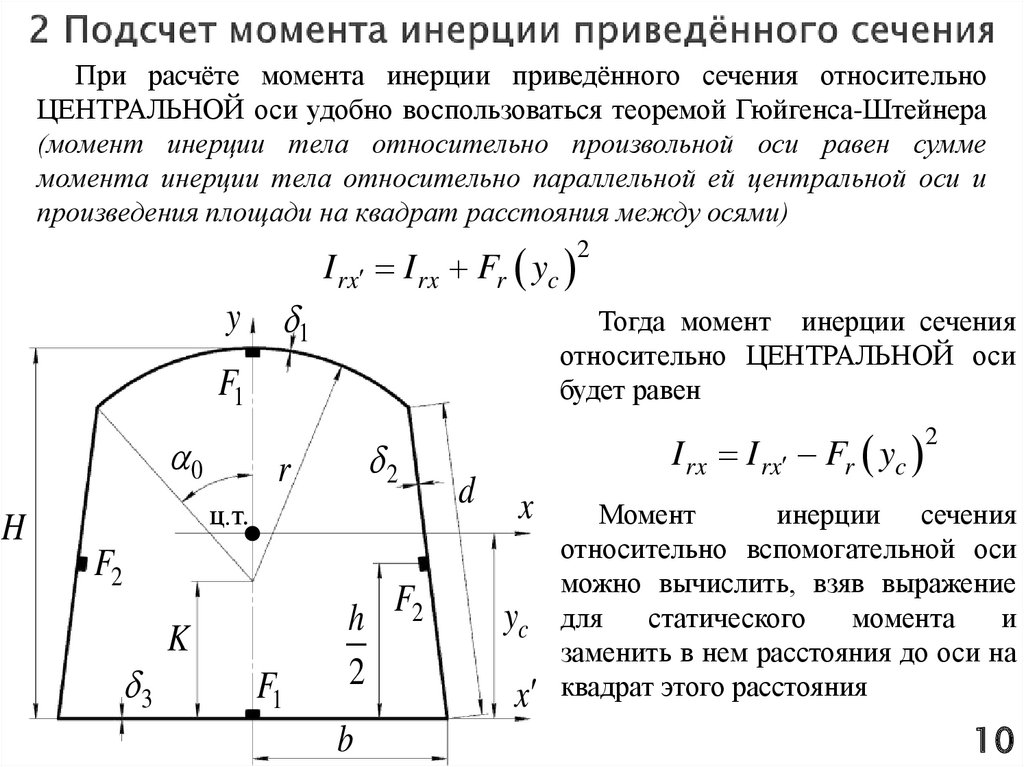
При расчёте момента инерции приведённого сечения относительно
ЦЕНТРАЛЬНОЙ оси удобно воспользоваться теоремой Гюйгенса-Штейнера
(момент инерции тела относительно произвольной оси равен сумме
момента инерции тела относительно параллельной ей центральной оси и
произведения площади на квадрат расстояния между осями)
y
1
I rx I rx Fr yc
Тогда момент инерции сечения
относительно ЦЕНТРАЛЬНОЙ оси
будет равен
F1
0
2
r
ц.т.
H
F2
3
K
F1
2
h
2
b
F2
d
I rx I rx Fr yc
x
yc
x
2
Момент
инерции сечения
относительно вспомогательной оси
можно вычислить, взяв выражение
для
статического
момента
и
заменить в нем расстояния до оси на
квадрат этого расстояния
10

11.

Момент инерции сечения относительно вспомогательной оси:
n
I rx об y ds п Fi yi
2
2
i 1
l
0
2
d
h
2
2
I rx об K r cos 1rd h s sin 2ds 2 п F1H 2 2 F2
0
2
0
Распишем подчеркнутый интеграл
0
y 1
F1
0
2
K
r
cos
1rd
0
r
H
3
h
2
K
F1
b
K
2
2 Kr cos r 2 cos 2 1rd
0
2
h
F2
s
0
d
K 2 1r 0 2 Kr 2 1 sin 0
F2
sin 2 0
r 3 1
0
2
2
x
11

12.

Момент инерции сечения относительно вспомогательной оси:
0
2
d
h
2
2
I rx об K r cos 1rd h s sin 2ds 2 п F1H 2 2 F2
0
2
0
Распишем подчеркнутый интеграл
d
2
h
s
sin
2ds
y 1
F1
0
0
d
s
2
h
F2
3
0
r
H
h 2 2hs sin s 2 sin 2 2ds
h
2
K
F1
b
h 2 2 d hd 2 2 sin
d3
2 sin 2
3
d
F2
x
12

13.

Момент инерции сечения относительно вспомогательной оси:
2
d
0
h
2
2
I rx об K r cos 1rd h s sin 2ds 2 п F1H 2 2 F2
2
0
0
3
2
sin 2 0
r
1
2
об K 1r 0 2 Kr 1 sin 0
0
2
2
2
2
d3
h
2
2
2
h 2d hd 2 sin 2 sin 2 п F1H 2 F2 ...
3
2
y 1
F1
0
s
r
H
2
h
F2
3
Упрощая выражение и,
числовые значения, получим
h
2
K
F1
b
подставив
I rx 599884382 мм 4
d
F2
x
13

14.

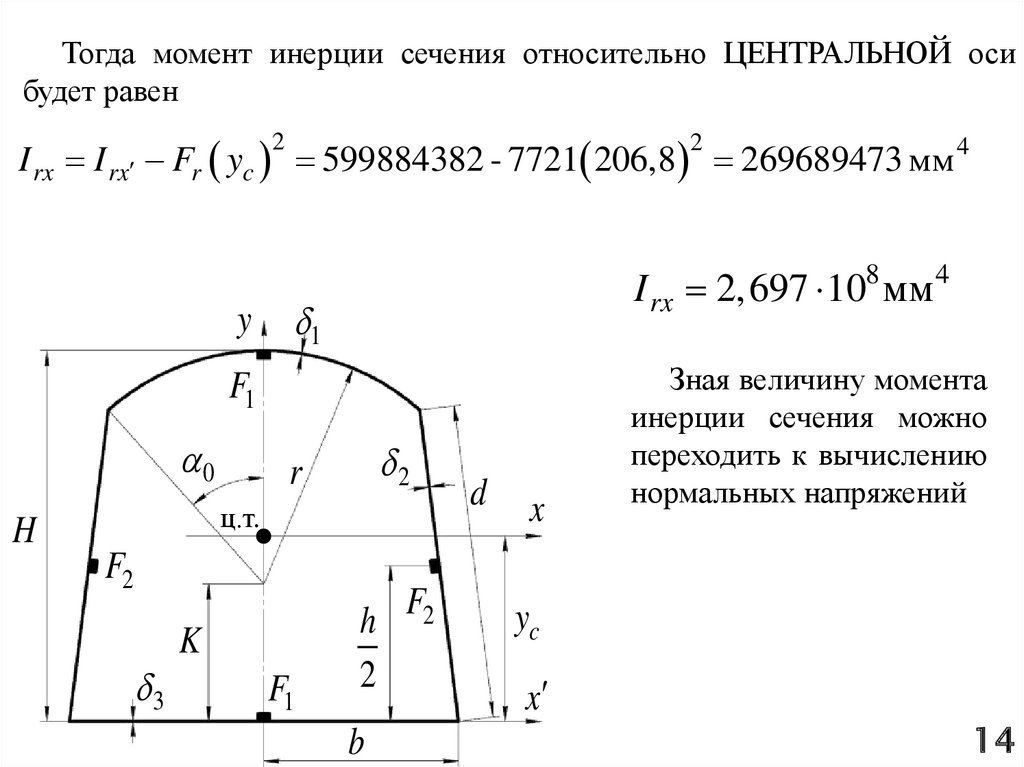
Тогда момент инерции сечения относительно ЦЕНТРАЛЬНОЙ оси
будет равен
I rx I rx Fr yc 599884382 - 7721 206,8 269689473 мм 4
2
2
I rx 2,697 10 мм
8
y
1
F1
0
2
r
ц.т.
H
F2
3
K
F1
F
h 2
2
b
d
x
4
Зная величину момента
инерции сечения можно
переходить к вычислению
нормальных напряжений
yc
x
14

15.

При расчёте момента инерции наклонного участка использовано
формальное интегрирование выражения и получен, хотя и верный, но
достаточно громоздкий результат.
d
d
d
2
2
2
y
ds
h
s
sin
ds
h
2
hs
sin
s
sin
2ds
2
2
2
0
2
0
0
d3
h 2d hd 2 sin 2 sin 2
3
Более простое выражение можно получить, если воспользоваться
формулой связи y’ и s чтобы перейти от интегрирования по ds к интегралу dy’
(обратите внимание на знаки дифференциалов и замену пределов
интегрирования)
y h s sin
2
2
dy
0
3 0
ds
dy 2 y
h3 2
2
2
y 2ds sin y 2 sin sin 3 3sin
0
h
h
s 0 y h
s d y 0
d
15

16.

При расчёте нормальных напряжений, возникающих в элементах сечения,
при действии изгибающего момента воспользуемся формулой
Вычислим коэффициент
Mx
y
I rx
Mx
80 106
Н
0,297 3
8
I rx 2,697 10
мм
Обратите внимание на размерности величин, используемых в формуле,
чтобы получать напряжения в естественных. единицах (МПа) необходимо
момент брать в Н‧мм, а момент инерции в мм4. В этом случае подставляя
координату y в мм получим напряжения в МПа.
0,297 y
Как видно напряжения изменяются линейно по сечению в зависимости
от y координаты, отсчитываемой от центральной (проходящей через центр
тяжести сечения) оси x. В точке с одинаковой ординатой y напряжения в
поясах и обшивки будут отличатся в φ раз (редукционный коэффициент).
16

17.

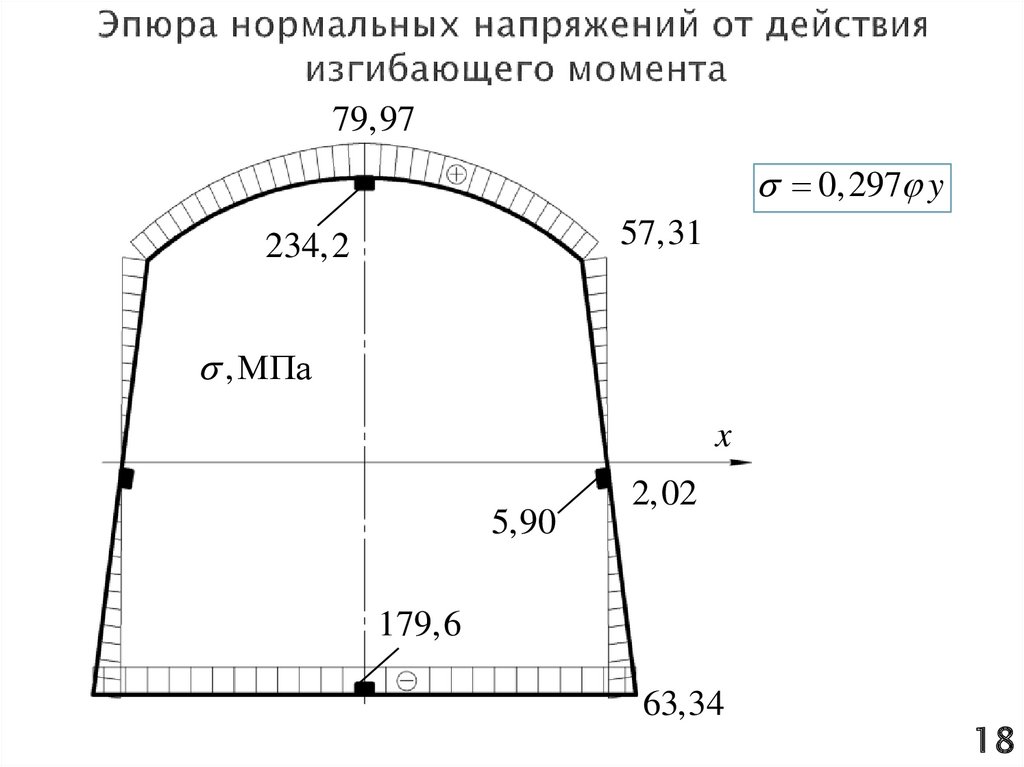
В верхней точке обшивки:
y H yc 476,4-206,8 269,6 мм
0,297 y
0,297 1 269,6 79,97 МПа
В верхнем поясе
0,297 2,93 269,6 234,2 МПа
В стыке дугового и наклонного участков:
y h yc 400-206,8 193,2 мм
0,297 1 193,2 57,31 МПа
h
400
В среднем поясе
y yc 206,8
6,8 мм
2
2
0,297 2,93 ( 6,8) 5,90 МПа
В обшивке под средним поясом 0,297 1 ( 6,8) 2,02 МПа
По нижнему участку обшивки: y yc = 206,8 мм
0,297 1 206,8 63,34 МПа
В нижнем поясе
0,297 2,93 206,8 179,6 МПа
17

18.

79,97
0,297 y
57,31
234,2
,МПа
x
5,90
2,02
179,6
63,34
18

19.

Как говорилось ранее сечение конструкции можно характеризовать как
однозамкнутое, симметричное относительно вертикальной центральной оси.
Для однозамкнутых сечений поток касательных сил представляет собой сумму
потока касательных сил, вычисленного для мысленно (виртуально) разрезанного
сечения, при простом изгибе и постоянного потока касательных сил по
замкнутому периметру контура, вызванного чистым кручением:
T T T0
Поток касательных сил мысленно (виртуально) разрезанного сечения при
простом изгибе пропорционален величине статического момента и
рассчитывается по формуле
T
Qy
I rx
Srx
Поток касательных сил по замкнутому периметру контура (суть – величина
касательной силы в продольном разрезе конструкции) при чистом кручении
рассчитывается по формуле
T0
M z T ds
Величины, входящие в последнюю формулу будут пояснены
по месту расчета.
19

20.

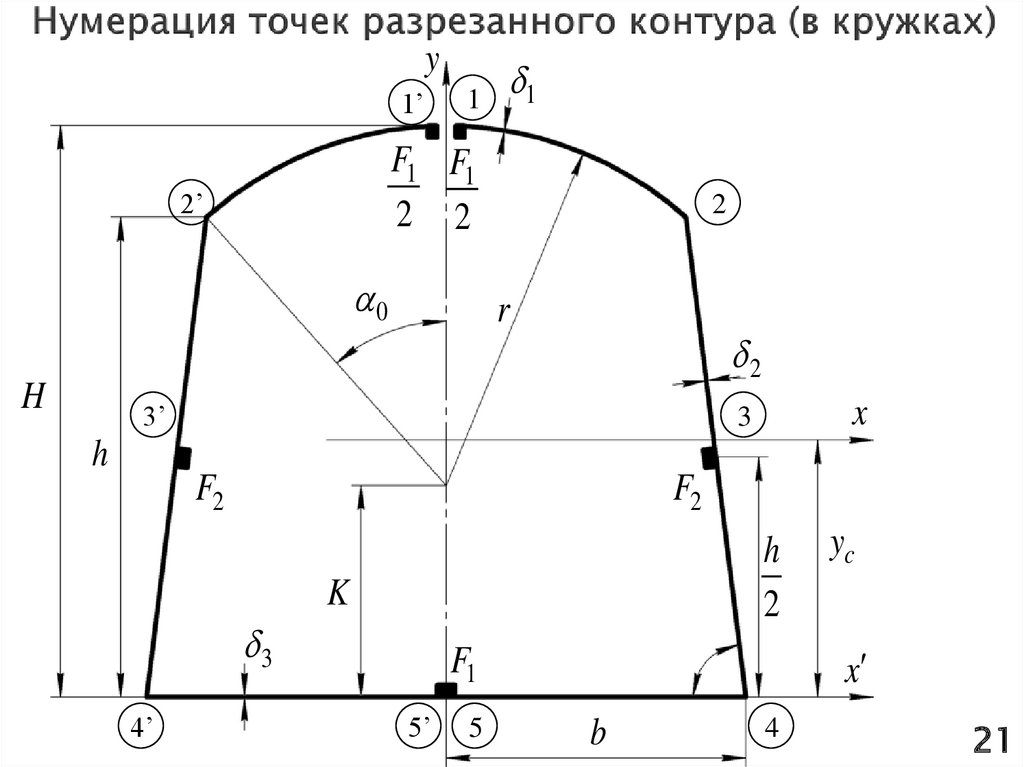
Для определения закона изменения статического момента по контуру сечения
необходимо выбрать точку условного (мысленного, виртуального) размыкания
контура.
Здесь можно выделить несколько важных соображений:
1) Точка условного размыкания контура выбирается в общем случае
произвольно, принципиальное условие состоит лишь в получении контура, не
имеющего замкнутых ячеек и не имеющего участков, не связанных с
остальными участками;
2) Сечение, обладающее вертикальной осью симметрии, рекомендуется
размыкать в одной из точек пересечения контура и этой оси (это позволит
получить симметричную эпюру статических моментов и, следовательно,
симметричный поток погонных касательных сил). Свойство симметрии
потока касательных сил (разомкнутного сечения) будет нами использовано
при вычислении T0.
3) Если в точке размыкания контура сечение подкреплено поясом, то
необходимо пояс разделить на две равные половины, каждую из которых
отнести к своей стороне сечения относительно разреза (для сохранения
симметрии сечения и после размыкания контура)
20

21.

y
1’
1
F1 F1
2 2
2’
0
H
1
2
r
2
3’
h
F2
F2
h
2
K
3
4’
x
3
x
F1
5’
5
yc
b
4
21

22.

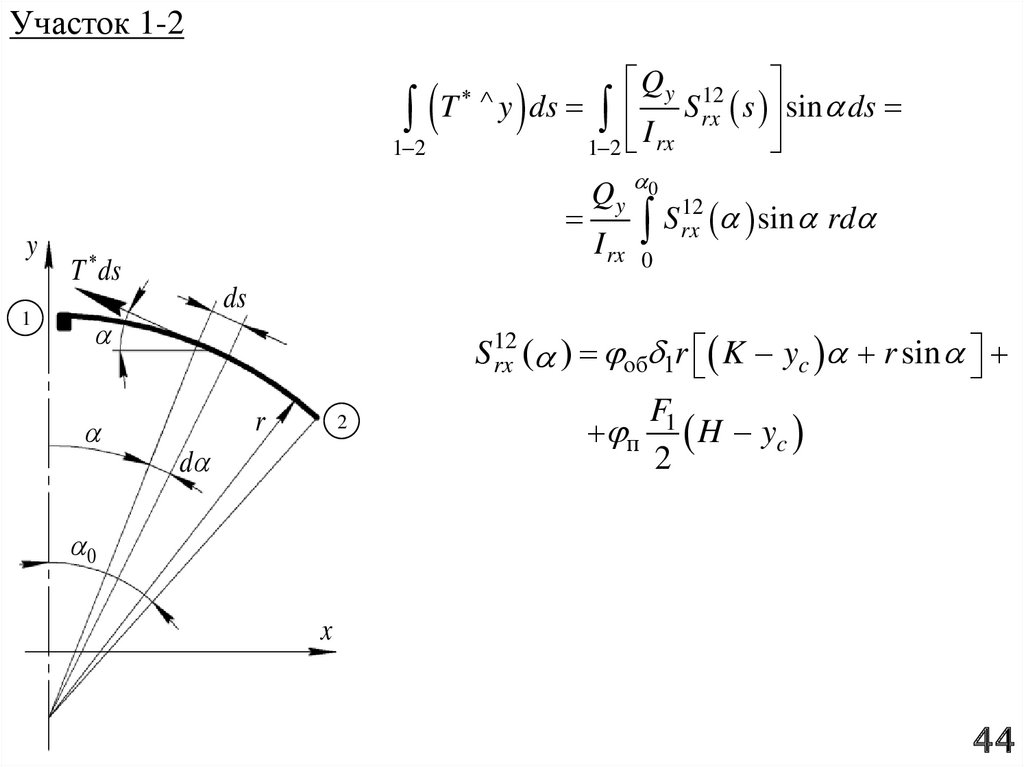
При расчёте статического момента будем обходить контур по часовой
стрелки начиная с точки 1. Расчёт будем вести по участкам 1-2, 2-3, 3-4 и 4-5.
В пределах участков соблюдаются – постоянство толщины обшивки контура
и монотонный характер изменения расстояния от точки контура до
центральной оси x. На границах (стыке) участков возможно скачкообразное
изменение величины статического момента при наличии продольного пояса в
этом стыке.
Закон изменения статического момента вычисляется по формуле
s
m
0
i 0
S rx s y ds i Fi yi
Где интегрирование проводится от начала отсчета дуг до текущей дуговой
координаты s, отсчитываемой вдоль контура, а в операторе суммирования
верхний предел соответствует числу поясов, попадающих в рассматриваемый
участок.
В случае криволинейного участка (дуги) в интегральном слагаемом
целесообразно перейти от дуговой координаты s к угловой мере этой дуги.
При записи закона изменения статического момента необходимо обеспечить
монотонное увеличение дуговой (вдольконтурной) координаты s.
При разрезе контура в нижней точке отсчет дуг следует вести против
направления часовой стрелки (учитывая знак y координаты точек контура)
22

23.

y
s
ds
1
F1
2
1
r
d
2
y K r cos
0
H
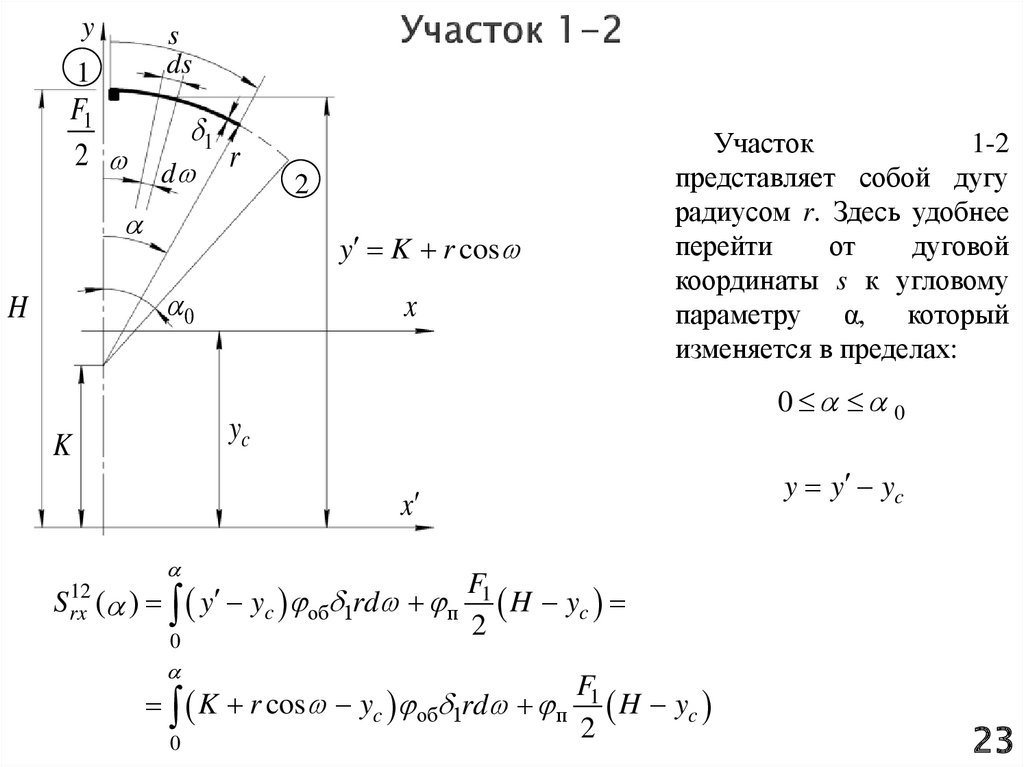
Участок
1-2
представляет собой дугу
радиусом r. Здесь удобнее
перейти
от
дуговой
координаты s к угловому
параметру α, который
изменяется в пределах:
x
0 0
yc
K
y y yc
x
12
S rx
y yc об 1rd п
0
F1
H yc
2
K r cos yc об 1rd п
0
F1
H yc
2
23

24.

12
S rx
об 1r K yc r sin п
В точке 1:
0
12
S rx
0 п
В точке 2:
F1
H yc
2
F1
350
5
3
H
y
2,93
1,382
10
мм
476,4
206,8
c
2
2
0
F1
H yc
2
1 2,5 300 176,4 206,8 0,7297 300 sin 0,7297
12
S rx
0 об 1r K yc 0 r sin 0 п
350
476,4 206,8 2,715 105 мм3
2
В пределах участка 1-2 зависимость статического момента от угла носит
практически линейный характер
2,93
24

25.

y
1
1
F1
2
2
r
2 s
0
x
3
y
yc
K
Участок 2-3 прямолинейный. Здесь
удобно пользоваться вдольконутрной
координатой
s.
(но,
учитывая
примечание {слайд 15} к вычислению
момента инерции сечения, возможно
интегрировать и по координате y’.
Нужно помнить лишь, что возрастание
s означает убывание y’)
d
2
y y yc
y h s sin
0 s
h
x
s
s
0
0
12
S rx23 s S rx
0 y yc об 2ds Srx12 0 h s sin yc об 2ds
S rx23 s
12
Srx
2
s
0 об 2 h yc s sin
2
25

26.

y
F1
2
Вариант с переходом к интегралу по
координате y’
1
1
2
r
d
0 s
2
y y yc
y h s sin
2 s
0
x
3
yc
K
y
h y
h
2
h y
s
sin
dy
ds
sin
h
x
Srx23 s
s
12
S rx
0 y yc об 2ds
S rx2 3
0
y
y
12
S rx
0 y yc об 2
h
dy
sin
h
об 2 y ' 2
об 2 h 2 y 2
23
12
12
Srx y S rx 0
yc y S rx 0
yc h y
sin 2
sin
y
2
26

27.

y
F1
2
Можно записать выражение для
статического
момента
записывая
вместо интеграла физический смысл
величины – произведение площади
отсеченного участка на расстояние от
оси до центра тяжести участка:
1
1
2
r
2 s
0
x
3
yc
K
y
h
x
12
Srx2 3 y S rx
0
Srx23
y
12
S rx
Через y’
Через s
площадь
отсеченного
участка
h y
об 2
sin
s об 2
расстояние от
центра тяжести
участка до оси x
h y
yc
2
s
h yc sin
2
h y
h y
об 2
yc
sin
2
об 2 h 2 y 2
0
yc h y
sin
2
12
S rx2 3 s S rx
0 s об 2 h yc s sin
2
2
12
S rx23 s S rx
0 об 2 h yc s s sin
2
Мы получили выражения, идентичные записанным ранее.
27

28.

Используем первое или
второе выражение, в
зависимости от
выбранного способа
S rx23
y
S rx23 s
12
Srx
12
Srx
об 2 h 2 y 2
0
yc h y
sin
2
2
s
0 об 2 h yc s sin
2
В точке 2:
s 0
y h
12
Srx23 y h S rx23 s 0 S rx
0 об 2 0 Srx12 0 2,715 105 мм3
h
2
об 2 h 2 h 2 2
h
23
12
S rx y Srx 0
yc h h 2
sin
2
2
об 2 3h 2
h ... 3,091 105 мм3
12
S rx 0
yc
sin 8
2
2
d
23
12
d
2
d
S rx s Srx 0 об 2 h y
sin
c
2
2
2
2
d
d
12
S rx 0 об 2 h yc sin ... 3,091 105 мм3
2 8
В точке 3:
s
d
2
y
28

29.

y
1
1
F1
2
r
2 s
0
3
K
Рассматривая первое или второе
выражение для статического момента
видно, что закон изменения имеет
квадратичный характер
2
yc
y
y
x
S rx23
h
S rx23 s
x
12
Srx
12
Srx
об 2 h 2 y 2
0
yc h y
sin
2
2
s
0 об 2 h yc s sin
2
Кроме того можно заметить, что участок 2-3
пересекает ось x, т.к.
h
yc 206,8 мм
200 мм
2
В точке пересечения участка 2-3 и оси x ожидаем максимальное значение
величины Srx. Убедимся в этом. Найдем значение аргумента при котором первая
производная Srx по аргументу обращается в нуль.
29

30.

S rx23
об 2 h 2 y 2
y
0
yc h y
sin
2
23
dS rx y об 2
y yc
dy
sin
12
Srx
2
s
0 об 2 h yc s sin
2
23
dS rx s
об 2 h yc s sin
ds
S rx23 s
12
Srx
Производная обращается в нуль (экстремум функции) когда обнуляется
выражение в скобках. Это соответствует точке с координатой
h yc
sin
Значение Srx в этой точке является максимальным для контура:
y ' yc
S rx23
y yc
12
Srx
или s
об 2 h 2 yc 2
5
3
0
yc h yc ... 3,092 10 мм
sin
2
2
h yc
h
y
h
y
1
12
5
3
c
c
Srx 0 об 2 h yc
...
3,092
10
мм
sin
sin
sin 2 sin
S rx23 s
30

31.

y
1
F1
2
2
2
3
F2
yc
x
s
h
2
y
Участок
3-4
прямолинейный,
наклонённый к горизонтали под углом β.
Он в целом похож на участок 2-3,
поэтому можно использовать любой из
трёх способов, предложенных для
участка 2-3 ранее (как прямую запись
интеграла от координаты s или y’, так и
запись
на
основе
физического
представления статического момента).
d
0 s
2
y y yc
x
4
y
h
s sin
2
h
34
23
y
Srx s Srx т. 3 п F2
c y yc об 2 ds
2
0
Обратите внимание на второе слагаемое, оно формально прибавляется (знак
плюс), но подчеркнутое выражение отрицательно, поэтому Srx уменьшится 31
s

32.

y
1
F1
2
h
34
S rx
s Srx23 т. 3 п F2 yc
2
2
s
2
3
F2
yc
x
h
34
Srx
s Srx23 т. 3 п F2 yc
2
s
h
2
y
h
s sin yc об 2 ds
2
0
Проинтегрировав выражение и приведя
подобные слагаемые получим
x
h
s2
об 2 yc s sin
2
2
4
Как видим зависимость статического момента на участке 3-4 также носит
квадратичный характер. Но экстремума здесь нет, в чем можно убедиться
приравняв нулю первую производную (самостоятельно проверьте, что
найденный экстремум лежит за пределами участка 3-4).
32

33.

y
1
F1
2
Запишем
выражение
для
статического
момента
подставляя
вместо интеграла физический смысл
величины – произведение площади
отсеченного участка на расстояние от
оси до центра тяжести участка:
2
2
3
F2
yc
x
s
h
2
x
4
34
Srx
y
S rx23
площадь
отсеченного
участка
y
Через y’
расстояние от
центра тяжести
участка до оси x
h 2 y
об 2
sin
Через s
s об 2
h 2 y y h y s sin
c
c
2
2
2
h 2 y
h 2 y
h
об 2
т. 3 п F2 yc
yc
2
sin
2
h
h
s
34
Srx
s Srx23 т. 3 п F2 yc s об 2 yc sin
2
2
2
33

34.

Используем выражение в зависимости от выбранного способа
h 2 y
h 2 y
h
34
23
Srx y Srx т. 3 п F2 yc
об 2
yc
2
sin
2
h
h
s
34
Srx
s Srx23 т. 3 п F2 yc s об 2 yc sin
2
2
2
В точке 3:
s 0
y
h
2
h
h
34
34
23
Srx
s 0 Srx
S
F
т.
3
п 2 yc
y
rx
2
2
400
5
3
3,091 105 2,93 250
206,8 ... 3,041 10 мм
2
В точке 4:
s
34
Srx
s
d
2
y 0
d
h
34
23
S rx y 0 S rx т. 3 п F2 yc
2
2
h
h
об 2 yc ... 2,611 105 мм3
2sin
4
34

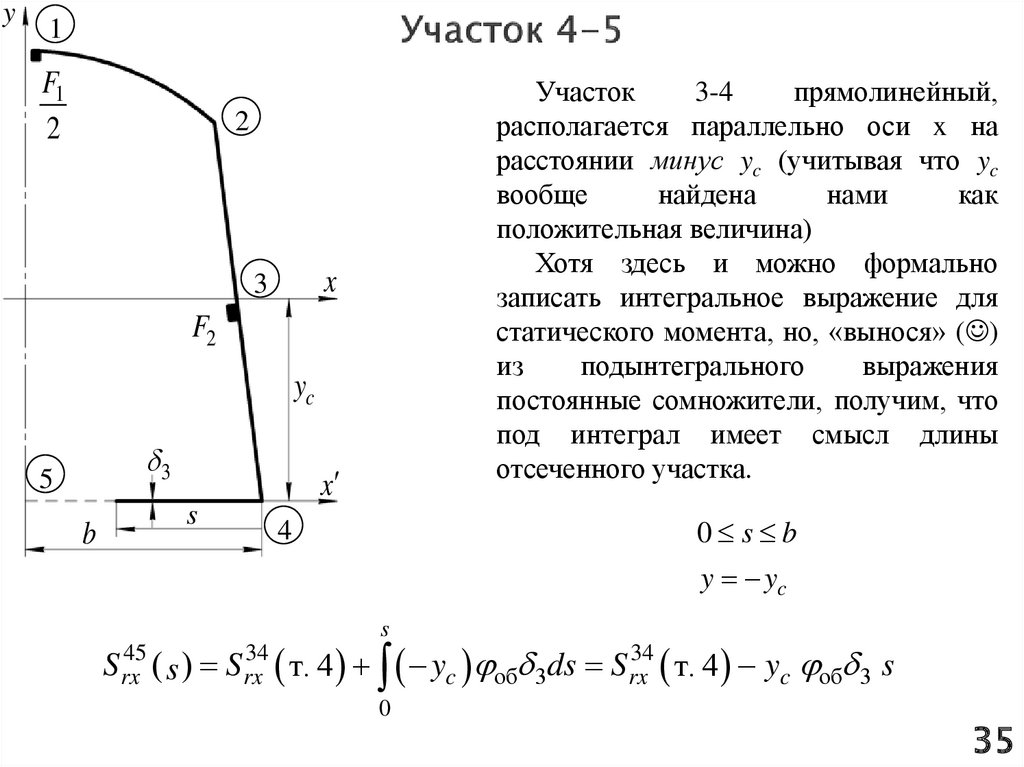
35.

y
1
F1
2
Участок
3-4
прямолинейный,
располагается параллельно оси x на
расстоянии минус yc (учитывая что yc
вообще
найдена
нами
как
положительная величина)
Хотя здесь и можно формально
записать интегральное выражение для
статического момента, но, «вынося» ( )
из
подынтегрального
выражения
постоянные сомножители, получим, что
под интеграл имеет смысл длины
отсеченного участка.
2
x
3
F2
yc
3
5
b
x
s
0 s b
4
y yc
s
34
S rx45 s S rx
т. 4 yc об 3ds Srx34 т. 4 yc об 3 s
0
35

36.

Как видно из выражения зависимость статического момента на участке
4-5 носит линейный характер. Для построения эпюры нам достаточно
знать два значения в крайних точках.
34
Srx45 s Srx
т. 4 yc об 3 s
В точке 4:
s 0
34
Srx45 s 0 Srx
т. 4 2,611 105 мм3
В точке 5:
s b
34
Srx45 s b S rx
т. 4 yc об 3 b
2,611 105 206,8 1 3 250 1,060 105 мм3
Точка 5 лежит на оси симметрии контура, поэтому дальнейшие участки не
требуют рассмотрения. Эпюра на участках слева от оси симметрии будет
получена путем симметричного отражения эпюры построенный по
рассчитанным значениям.
Но прежде чем переходить к построению эпюры выполним ПРОВЕРКУ
36

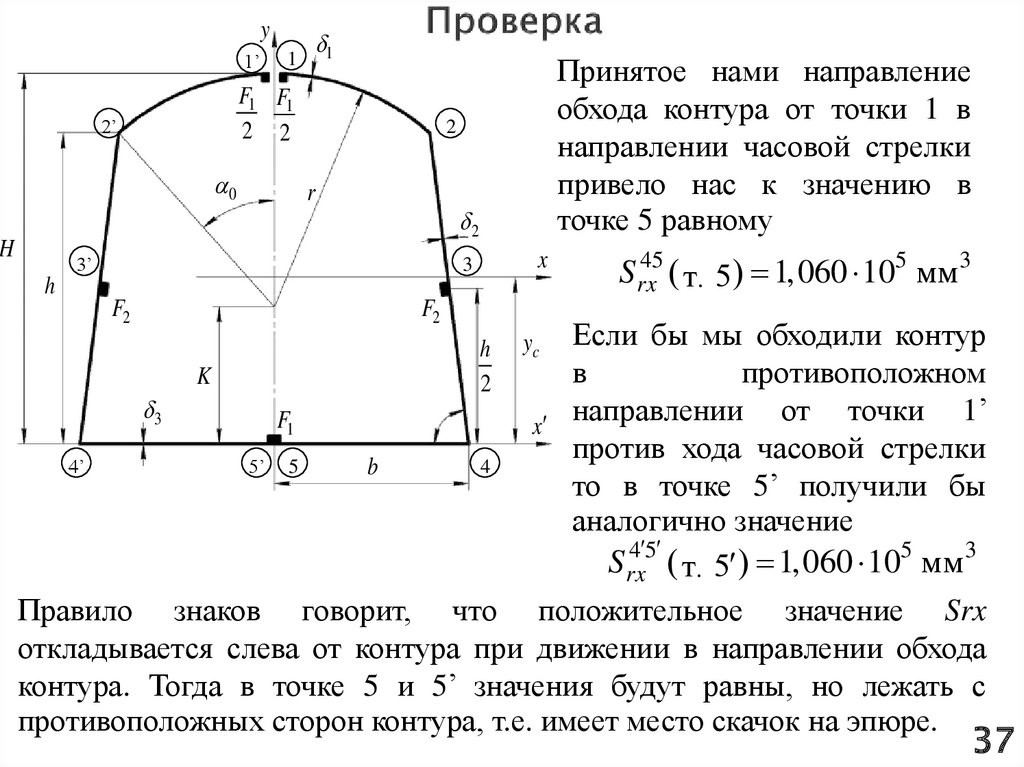
37.

y
1’
1
F1 F1
2 2
2’
0
H
1
2
r
2
3’
h
x
3
F2
F2
h
2
K
3
4’
Принятое нами направление
обхода контура от точки 1 в
направлении часовой стрелки
привело нас к значению в
точке 5 равному
x
F1
5’
5
yc
b
4
Srx45 т. 5 1,060 105 мм3
Если бы мы обходили контур
в
противоположном
направлении от точки 1’
против хода часовой стрелки
то в точке 5’ получили бы
аналогично значение
Srx4 5 т. 5 1,060 105 мм3
Правило знаков говорит, что положительное значение Srx
откладывается слева от контура при движении в направлении обхода
контура. Тогда в точке 5 и 5’ значения будут равны, но лежать с
противоположных сторон контура, т.е. имеет место скачок на эпюре.
37

38.

y
1’
1
F1 F1
2 2
2’
0
H
1
2
r
2
3’
h
3
F2
SrxF1 т.5 п F1 yc
F2
h
2
K
3
4’
Убедимся, что величина
скачка при переходе 5-5’
соответствует статическому
моменту пояса,
расположенного в точке 5 (5’)
x
x
F1
5’
5
yc
b
2,93 350 206,8
2,120 105 мм3
4
Правило проверки: если в точке, противоположенной разрезу имеется
пояс, то значение статического момента последнего участка в этой
точке должно по равняться половине статического момента пояса,
взятого по абсолютной величине . Если пояс в этой точке отсутствует,
то статический момент на оси симметрии должен обращаться в нуль.
F1
S
2,120 105
45
5
rx т.5
Srx т. 5 1,060 10
1,060 105
2
2
Равенство верное, проверка пройдена.
38

39.

y
Обратите внимание,
что изображена эпюра
умноженная на 10-5
1,382
F1
2
F1
2
2,715
3,092 max
Srx 10 5 , мм3
x
F2
F2
3,091
3,041
F1
1,060
2,611
Правила построения эпюры статического момента – положительная
величина откладывается слева при движении вдоль контура в
направлении обхода от точки размыкания (отрицательная – справа)
39

40.

T
Qy
I rx
Srx
Для получения эпюры погонных касательных сил необходимо эпюру
статического момента умножить на коэффициент
Qy
I rx
30 103
5 Н
11,12 10
8
2,697 10
мм 4
T 11,12 10 5 Srx
При построении эпюры погонных касательных сил для разомкнутого
сечения следует учитывать, что погонная сила это векторная величина,
следовательно кроме эпюры, отложенной от линии контура следует
проставить направление потока касательных сил по каждому из участков.
Используем следующее правило – если при движении по направлению
обхода контура эпюра отложена слева, то поток касательных сил
направлен против направления обхода. В противном случае поток
касательных сил направлен по возрастанию вдольконтурной координаты.
При переходе эпюры через линию контура – направление потока
касательных сил меняется на противоположное.
40

41.

y
F1
2
T 11,12 10 5 Srx
15,37
30, 21
F1
2
34,39
Н
T ,
мм
x
F2
F2
34,38
33,83
F1
Qy
11,79
29,04
41

42.

Суть проверки – результирующая эпюры погонных касательных
сил, спроецированная на ось y должна по величине и направлению
совпадать с перерезывающей силой Qy
T y ds Qy
Интеграл по контуру можно заменить суммой интегралов по
отдельным участкам (а в силу симметрии эпюры погонных
касательных сил можно рассмотреть половину сечения и удвоить
результат).
T
y ds 2 T y ds T y ds T y ds T y ds
2 3
3 4
4 5
1 2
42

43.

При
вычислении
проекции
результирующей
погонной
касательной силы на отдельном участке в зависимости от
характера эпюры и ориентации участка можно вычислять
результирующую как площадь эпюры на этом участке. Однако это
упрощение хорошо работает только если эпюра подчиняется
линейному закону. В случае квадратичной зависимости следует
применять метод Симпсона (который требует знания значений
эпюры на концах и в середине участка).
В
самом
общем
случае
качественный
результат
даёт
подстановка в подынтегральное выражение
T
Qy
I rx
Srx
43

44.

Участок 1-2
T
1 2
y
1
Qy 12
y ds S rx s sin ds
I
1 2 rx
T ds
I rx
12
Srx
sin rd
0
ds
Qy 0
12
Srx
об 1r K yc r sin
r
2
d
п
F1
H yc
2
0
x
44

45.

1 2
0
Q
F1
y
H
y
T y ds
r
K
y
r
sin
c sin rd
об 1
c
п
I rx 0
2
0
0
2
2
об 1r K yc sin d r sin d
I rx
0
0
Qy
0
F1
п H yc r sin d
I rx
2
0
Qy
Вычислим интегралы отдельно
0
sin d sin 0 0 cos 0
0
0
sin 2 0
sin d 2 4
0
2
0
0
sin d cos 0
0
45

46.

T
1 2
y ds
2
Qy
об 1r K yc sin 0 0 cos 0
I rx
0 sin 2 0 Qy
F1
r
п H yc r cos 0
4
2
2
I rx
Подставляя числовые величины и вычисляя, получим:
1 2
T y ds ... 1955 Н
46

47.

Участок 2-3
Участок прямолинейный, сохраняется постоянный угол наклона β
2 3
d 2
Q
Q
y 23
y
T y ds S rx s sin ds
sin S rx23 s ds
I
I rx
2 3 rx
0
Srx23 s
T
2 3
y ds
Qy
I rx
12
Srx
2
s
0 об 2 h yc s sin
2
d 2
sin
0
2
12
s
S rx 0 об 2 h yc s sin ds
2
2
3
d
2
d
2
d
12
sin Srx
sin
0 об 2 h yc
I rx
2
2
6
... 6608 Н
Qy
47

48.

Участок 3-4
Участок прямолинейный, сохраняется постоянный угол наклона β
3 4
Qy
Qy 34
T y ds S rx s sin ds
sin
I
I rx
3 4 rx
d 2
34
S rx
s ds
0
h
h
s
34
Srx
s Srx23 т. 3 п F2 yc s об 2 yc sin
2
2
2
T
3 4
y ds
Qy
I rx
d 2
sin
0
23
s
h
s h
ds
S
F
т.
3
y
y
sin
п 2
об 2
c
c
rx
2
2
2
2
3
d
2
d
2
d
h
h
23
sin Srx т. 3 п F2 yc об 2 yc
sin
2
I rx
6
2
2
2
... 6437 Н
Qy
48

49.

Участок 4-5
Участок прямолинейный, располагается перпендикулярно оси y, а
следовательно проекция равнодействующей погонной касательной
силы на этом участке будет равна нулю.
T y ds 0
4 5
T
Результирующая эпюры погонных касательных сил,
спроецированная на ось y :
y ds 2 T y ds T y ds T y ds T y ds
1 2
2 3
3 4
4 5
2 1955 6608 6437 0 30000
Полученная величина в точности равна перерезывающей силе,
действующей в рассчитываемом сечении.
При выполнении курсовой работы допустимо расхождение до 3%
49

50.

Постоянная составляющая касательных сил действует по замкнутой
части контура. Её природу можно объяснить тем фактом, что вектор
перерезывающей силы в расчётном сечении не проходит через центр
изгиба разомкнутого сечения. Фактически постоянную составляющую
погонных касательных сил следует рассматривать как неизвестную
касательную силу, которая стягивает края продольного разреза, чтобы
разомкнутый контур сохранял исходную форму поперечного сечения при
приложении поперечной нагрузки.
Постоянную составляющую погонных касательных сил можно найти
по формуле
T0
M z T ds
M z – момент внешней силы относительно выбранного полюса
– плечо элементарной силы T*ds относительно выбранного полюса
– удвоенная площадь, охватываемая замкнутой линией контура 50

51.

Рассматривая структуру формулы и величины, входящие в нее,
можно отметить тот факт, что сложность расчёта будет определятся
выбором (в общем случае произвольным) полюса.
Выбирая полюс следует помнить, что эпюра погонных сил T*
симметрична относительно вертикальной оси симметрии, поэтому
выбирая полюс на оси y можно утверждать, что
T
ds 0
В таком случае формула расчёта постоянной составляющей погонных
касательных сил примет вид
Mz
T0
Момент внешней силы относительно выбранного полюса в этом
случае будет представлять произведение величины силы на расстояние
между вектором силы и осью симметрии
M z Qy c
Момент внешних сил (и момент элементарных сил T*ds) следует
принимать положительным, если он действует относительно полюса
против часовой стрелки. В противном случае момент принимается
отрицательным.
51

52.

Величина,
стоящая
в знаменателе формулы постоянной
составляющей погонных сил, представляет собой удвоенную площадь
замкнутой ячейки контура:
ds
Касательно постоянной составляющей погонных касательных сил T0
следует отметить, что это векторная величина (как и погонная
касательная сила T*), поэтому необходимо принять правило для знаков и
направлений:
Положительная величина T0 вызывает положительный момент
относительно полюса, направленный против хода часовой стрелки и
эпюра T0 откладывается снаружи контура, а направление потока – против
часовой стрелки.
В случае отрицательной величины T0 – вызываемый момент
отрицательный и направлен по направлению хода часовой стрелки,
эпюра T0 откладывается внутрь контура, а стрелки потока направлены по
часовой стрелке.
Следует напомнить, что если контур комбинированный и содержит
замкнутую ячейку и свободные участки (фланцы), то постоянная
составляющая погонных касательных сил действует исключительно по
52
замкнутой ячейке, а на свободных участках – отсутствует.

53.

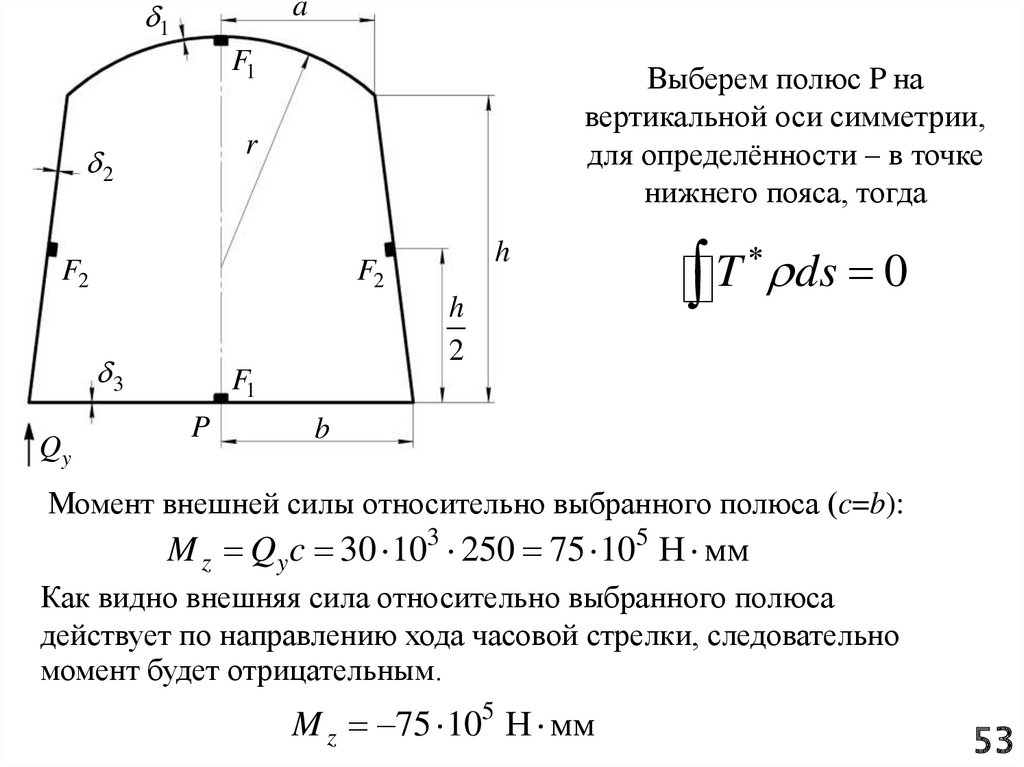
1
a
F1
Выберем полюс P на
вертикальной оси симметрии,
для определённости – в точке
нижнего пояса, тогда
r
2
F2
h
2
3
Qy
h
F2
T
ds 0
F1
P
b
Момент внешней силы относительно выбранного полюса (c=b):
M z Qy c 30 103 250 75 105 Н мм
Как видно внешняя сила относительно выбранного полюса
действует по направлению хода часовой стрелки, следовательно
момент будет отрицательным.
M z 75 105 Н мм
53

54.

1
a
F1
r
2
F2
F2
3
Qy
F1
P
b
Контур образует замкнутую
ячейку и не содержит свободных
фланцев. Вычислим площадь,
охватываемую средней линией
контура. Она складывается из
площади кругового сегмента и
h
площади трапеции.
h
1 2
2a 2b
A
r
2
sin
2
h
0
2
0
2
2
площадь кругового
сегмента
площадь трапеции
2 200 2 250
1
2 A 2 3002 2 0,7297 sin 2 0,7297
400 443817 мм 2
2
2
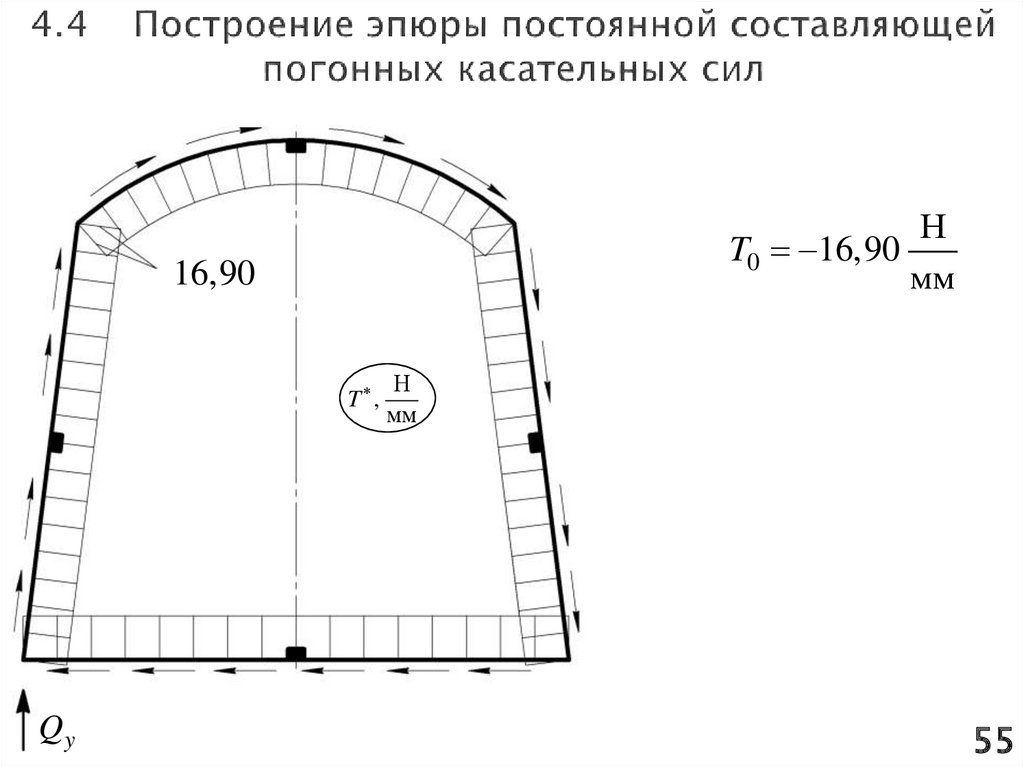
Вычислим постоянную составляющую погонных касательных сил
M z 75 105
Н
T0
16,90
443817
мм
Получили отрицательную величину, следовательно поток будет направлен
по ходу часовой стрелки и эпюра отложена внутрь контура.
54

55.

T0 16,90
16,90
T ,
Qy
Н
мм
Н
мм
55

56.

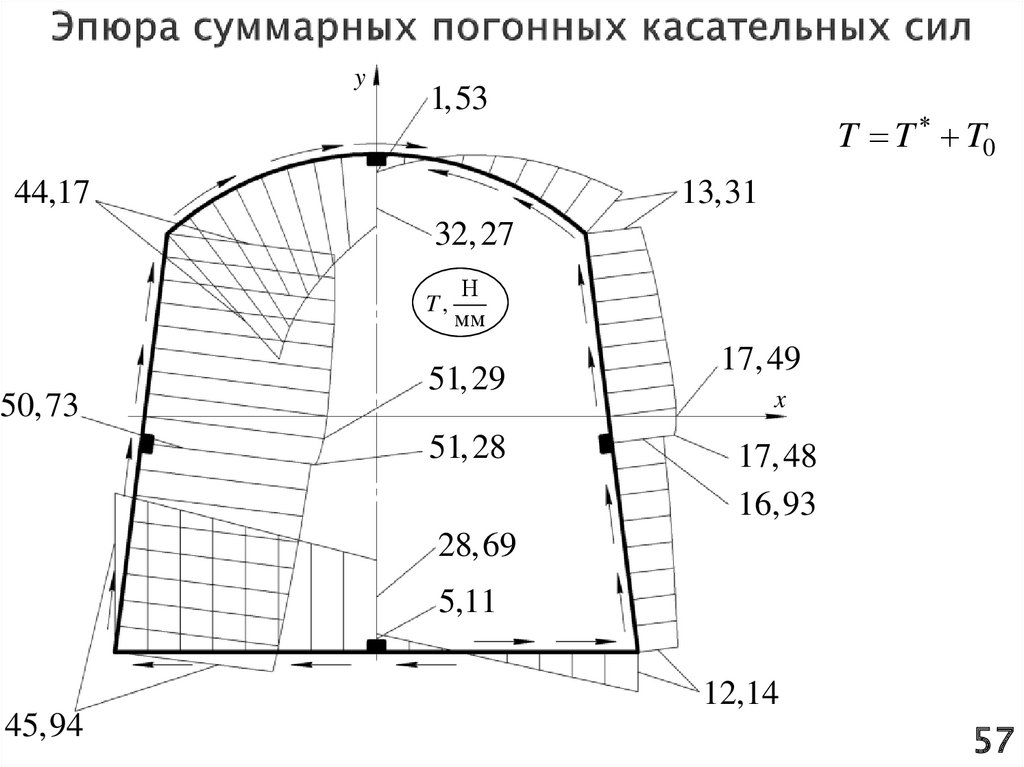
При вычислении эпюры суммарных погонных касательных сил
необходимо применить принцип суперпозиции и векторно сложить
эпюру погонных касательных сил разомкнутого сечения T* и эпюру
постоянной составляющей погонных касательных сил T0.
Векторное сложение подразумевает, что если стрелки обоих потоков
на участке направлены в одну сторону, то эпюры необходимо
суммировать и направление результирующего потока совпадает с
направлениями отдельных потоков.
В том случае, если направление потоков T* и T0 противоположно, то
следует из числового значения того потока, который больше, вычесть
значение меньшего потока и результат отложить (наружу или внутрь)
контура, а также направление потока – как у эпюры с большим числовым
значением.
При сложении эпюр следует помнить, что T0 является постоянной
составляющей, которая одинакова во всех точках контура. Поэтому
сложение или вычитание этой эпюры – есть по сути параллельный
перенос T* (смещение линии эпюры) в нужном направлении.
56

57.

y
1,53
T T T0
13,31
44,17
32, 27
T,
50,73
Н
мм
51, 29
51, 28
17, 49
x
17, 48
16,93
28,69
5,11
12,14
45,94
57

58.

Для вычисления величины касательных напряжений, действующих
на участке контура, необходимо величину потока касательных сил на
этом участке поделить на толщину обшивки участка. Характер и
направление потока касательных напряжений будут соответствовать
поток погонных касательных сил.
Построение эпюры оставлено на самостоятельную работу

59.

Контакты для обратной связи:
GlushkovSergeyV@mail.ru
https://vk.com/glushkov_sv
59