Similar presentations:
Пересечение линии и поверхности
1.
ПЕРЕСЕЧЕНИЕ ЛИНИИ ИПОВЕРХНОСТИ
Горячкина А.Ю.
2.
Линия и поверхность пересекаются в одной илинескольких точках.
Точки
пересечения
линии
и
поверхности
принадлежат одновременно обеим фигурам.
Если
одна
из
пересекающихся
фигур
-
проецирующая, то проекция точки пересечения фигур
принадлежит
следу
проецирующей
фигуры,
вторую
проекцию точки строят из условия ее принадлежности
непроецирующей фигуре
3.
Случай, когда одна из геометрических фигур - проецирующаяα
π1 , а – общего положения
α"
a"
K"
x
a'
h0α≡ α'
K'
h0α ,
K'
K"
а"
Рис. 10.1
4.
Случай, когда одна из геометрических фигур - проецирующаяа
π1 , α - общего положения
a"
α"
K '≡ а' , K"
α"
l"
K"
x
a' ≡ K'
α'
l'
Рис. 10.2
5.
Случай, когда обе геометрические фигуры – общего положенияАлгоритм решения:
1. Заключить
линию
а
вспомогательную поверхность ϒ
во
2. Построить линию
l
пересечения
вспомогательной поверхности ϒ
с
заданной поверхностью
Рис. 10.3
3. Отметить искомую точку
К
пересечении заданной линии
а
построенной линией l
на
с
6.
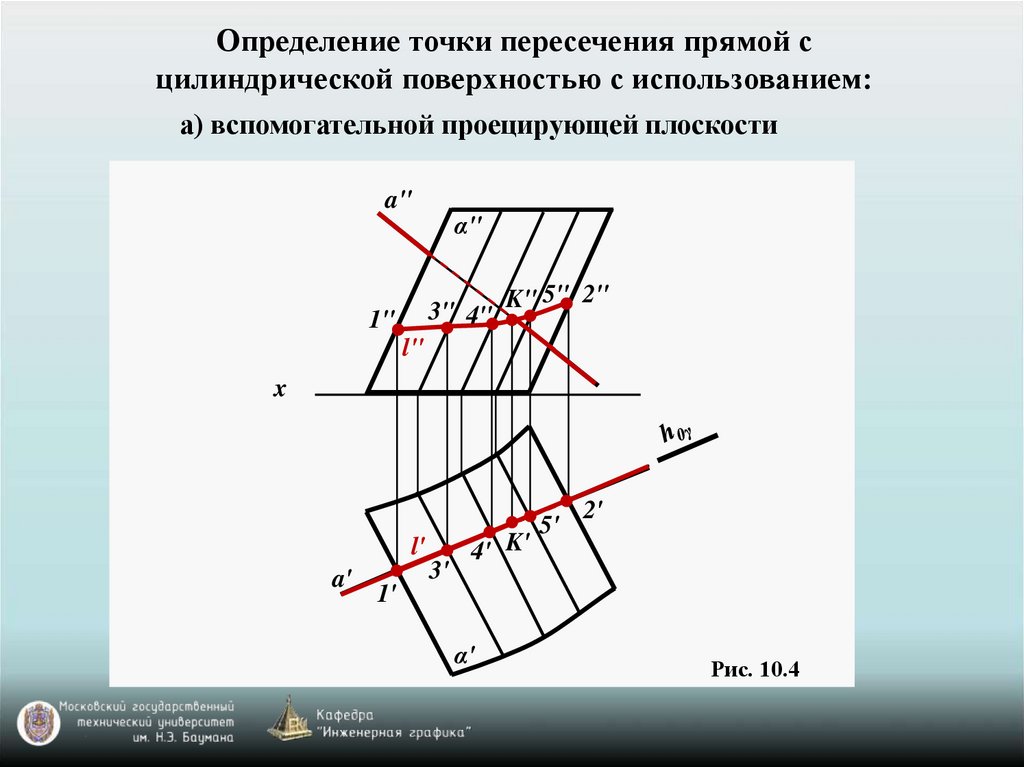
Определение точки пересечения прямой сцилиндрической поверхностью с использованием:
а) вспомогательной проецирующей плоскости
a"
α"
5" 2"
3" 4" K"
1"
l"
x
l'
a'
3'
4' K'
5'
2'
1'
α'
Рис. 10.4
7.
Определение точки пересечения прямой сцилиндрической поверхностью с использованием
б) вспомогательной плоскости общего положения
γ"
1"
α"
a"
b"
K"
x
Hb"
Ha"
Hb'
Ha'
b'
K'
a'
1'
γ'
α'
Рис. 10.5
8.
Касательная плоскостьи
нормаль к поверхности
Горячкина А.Ю.
9.
Плоскость, касательная к поверхности в заданной точке –есть множество касательных, проведенных к поверхности через
заданную точку
Касательная t к поверхности –
прямая, касательная к какой-либо
линии, принадлежащей поверхности
Рис. 9.1
Нормаль n к поверхности в заданной
точке – перпендикуляр к касательной
плоскости к поверхности в заданной
точке
Линию пересечения поверхности с
плоскостью,
проходящей
через
нормаль, называют нормальным
сечением
10.
Задание плоскости, касательной к поверхности в заданной точкеТ.к. плоскость определяется двумя пересекающимися
прямыми, то для задания плоскости, касательной к поверхности в
заданной точке, проводят две линии, принадлежащие поверхности и к
ним строят касательные
Алгоритм построения плоскости,
касательной к поверхности в точке А:
1. Провести линии-посредники а и в, принадлежащие поверхности,
и проходящие через точку А (линии-посредники на данной поверхности
следует выбирать так, чтобы они проецировались как простейшие
(прямые, окружности)
2.
Построить прямые t1 и t2 , касательные к линиям а и в в точке А
3. Плоскость τ , заданная прямыми t1 и t2 , будет касательной к
поверхности в заданной точке А
11.
Точка А – эллиптическая точка:- касание в точке;
- поверхность расположена по одну сторону
от касательной плоскости
Поверхности,
состоящие
только
из
эллиптических точек, являются выпуклыми и
называются поверхностями положительной
кривизны (сфера, эллипсоид, параболоид)
Рис. 9.2
12.
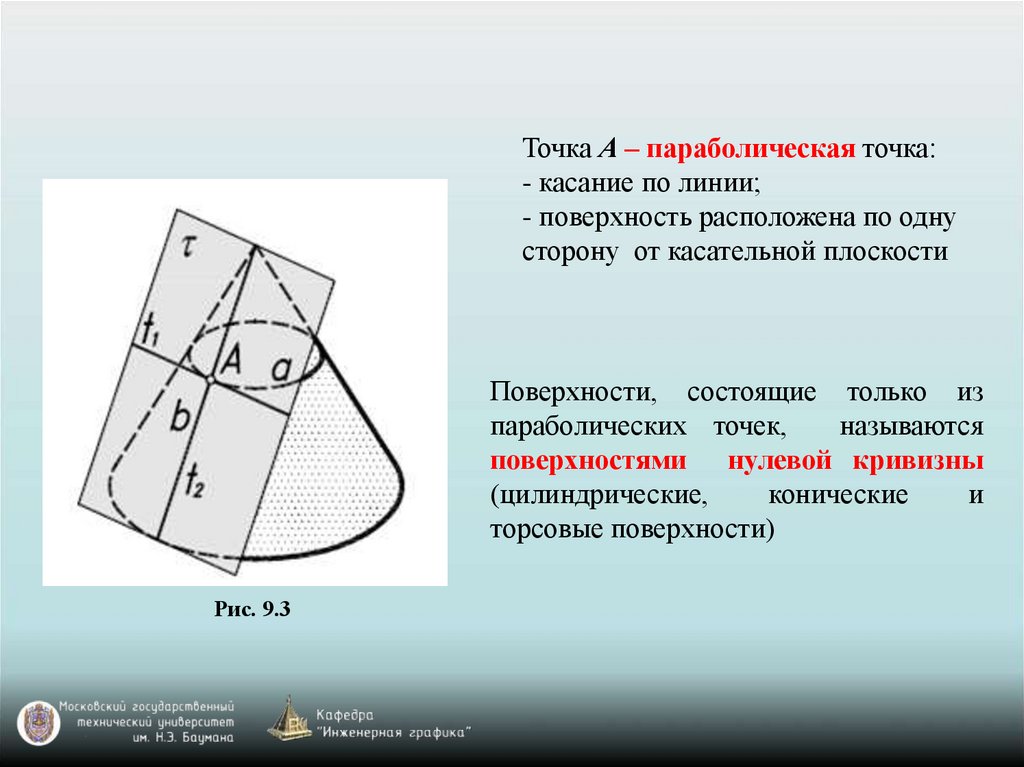
Точка А – параболическая точка:- касание по линии;
- поверхность расположена по одну
сторону от касательной плоскости
Поверхности, состоящие только из
параболических точек,
называются
поверхностями нулевой кривизны
(цилиндрические,
конические
и
торсовые поверхности)
Рис. 9.3
13.
Точка А – гиперболическая точка:- касание в точке;
- касательная плоскость пересекает
поверхность по линиям
Рис. 9.4
Поверхности, состоящие только из
гиперболических
точек,
являются
вогнутыми
и
называются
поверхностями
отрицательной
кривизны
(эллиптический
и
параболический гиперболоиды)
Поверхности, содержащие все виды точек,
поверхностями двоякой кривизны (поверхность тора)
называются
14.
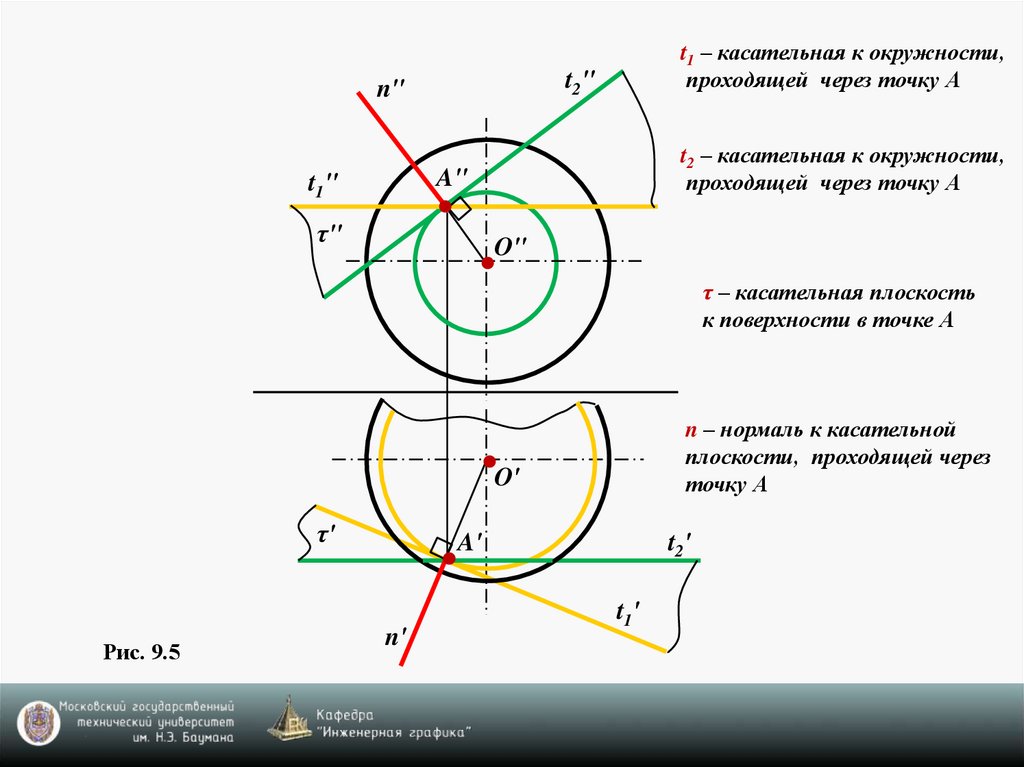
t1 – касательная к окружности,проходящей через точку А
t2"
n"
t2 – касательная к окружности,
проходящей через точку А
A"
t1"
τ"
O"
τ – касательная плоскость
к поверхности в точке А
n – нормаль к касательной
плоскости, проходящей через
точку А
O'
τ'
Рис. 9.5
A'
n'
t2'
t1'
15.
Конус касательных и конус нормалейк поверхности вращения
t1 , t2 , … - касательные к
меридианам, проходящим через
точки, лежащие на окружности с
п1 , n2 , … - нормали к
касательным
плоскостям,
проходящим
через
точки,
лежащие на окружности с
S1 вершина конуса
касательных к поверхности
вращения
S2 - вершина конуса нормалей
к поверхности вращения
Рис. 9.6
16.
S1 "n"
τ"
n0 "
t1 "
A"
A0"
t0 "
S1 – вершина конуса
касательных к поверхности
вращения
t1 – касательная к окружности,
проходящей через точку А
S2"
t2 – касательная к меридиану,
проходящему через точку А
t2 "
x
τ – касательная плоскость
к поверхности в точке А
n0'
A0' t0' S1'≡ S2'
τ'
A'
t2' ≡ n'
Рис. 9.7
t1 '
S2 – вершина конуса
нормалей к поверхности
вращения
n – нормаль к касательной
плоскости, проходящей через
точку А













 drafting
drafting








