Similar presentations:
Понятие об отображении. Образ и прообраз, биекция
1.
Часть 4 Тема 1Понятие об отображении
Образ и прообраз, биекция
2.
1. Определение отображенияВ этом видео
2. Понятие об образе и
прообразе
3. Инъективность,
сюръективность и
биективность
3.
Отображением множества вомножество называется некоторое
правило , при котором каждому
элементу соответствует один и
только один элемент .
4.
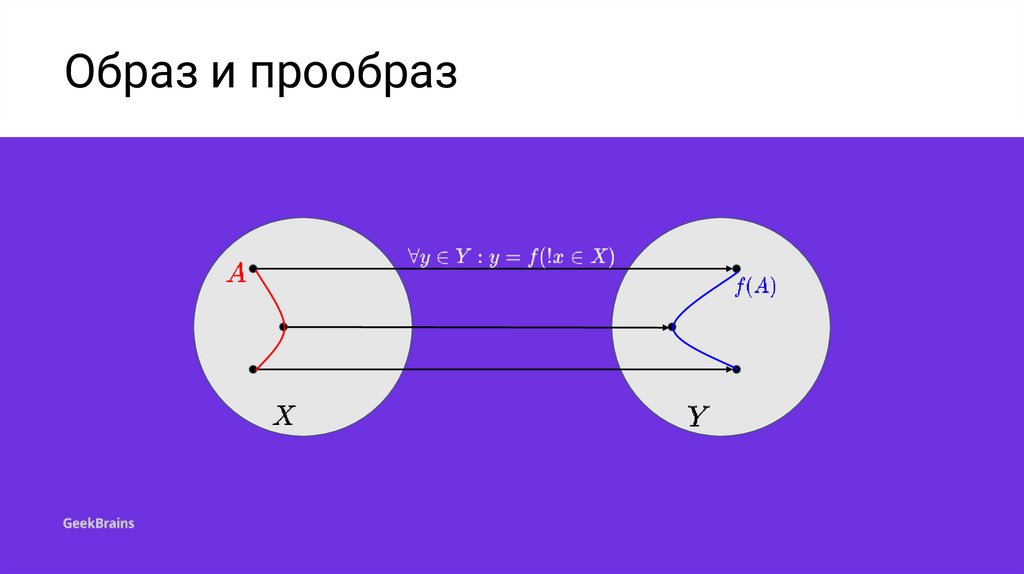
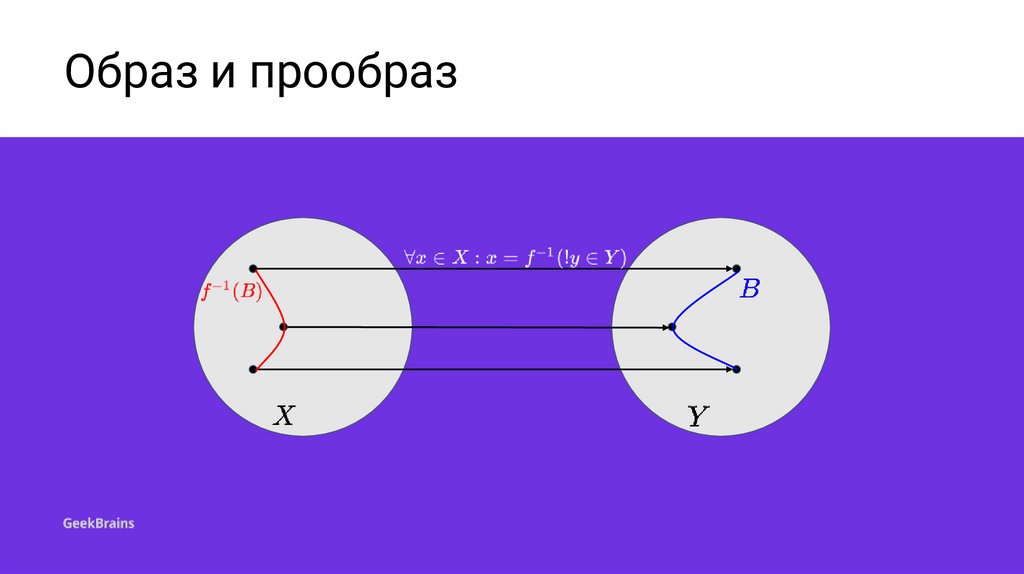
Понятие об образе ипрообразе
5.
Образ и прообраз6.
Свойства образа7.
Образ и прообраз8.
Свойства прообраза9.
Пример отображения10.
Инъективность, сюръективность ибиективность отображений
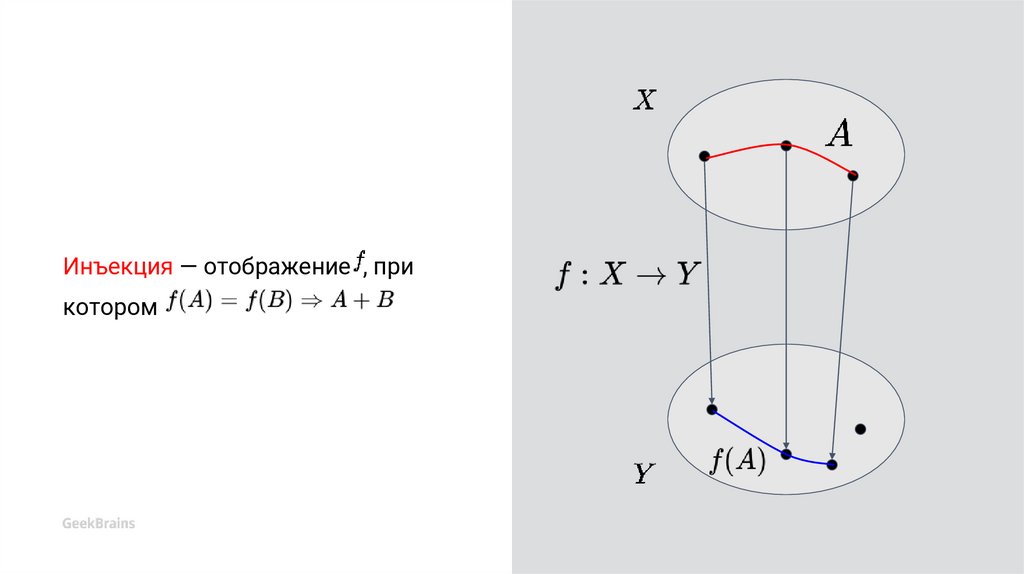
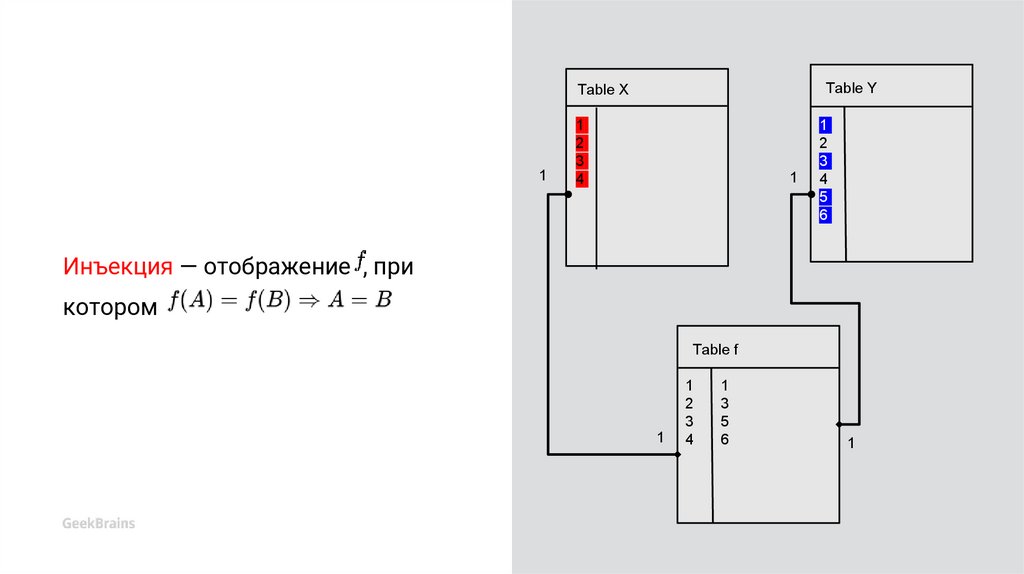
11.
Инъекция — отображение , прикотором
12.
Table YTable X
1
1
2
3
4
1
1
2
3
4
5
6
Инъекция — отображение , при
котором
Table f
1
1
2
3
4
1
3
5
6
1
13.
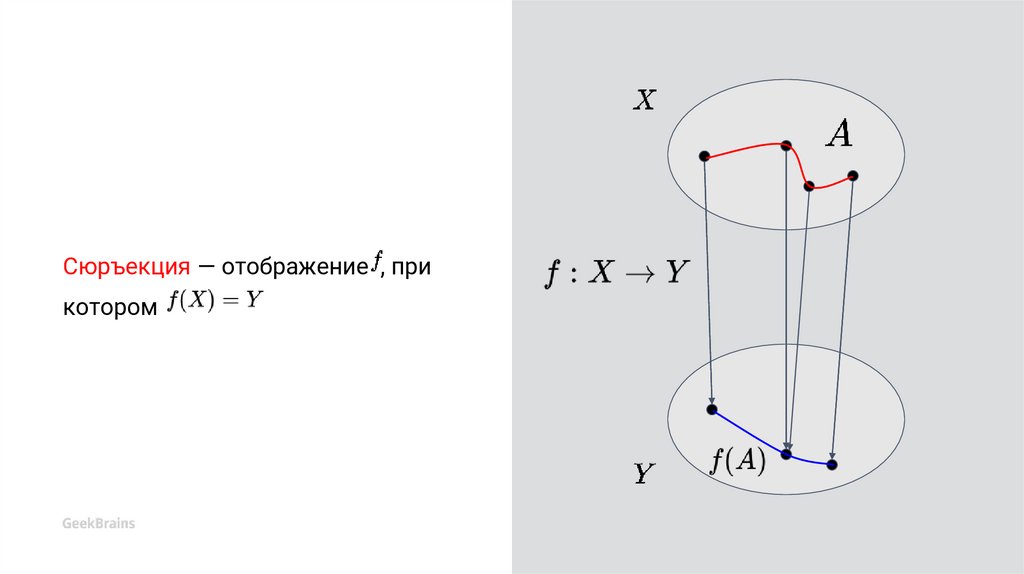
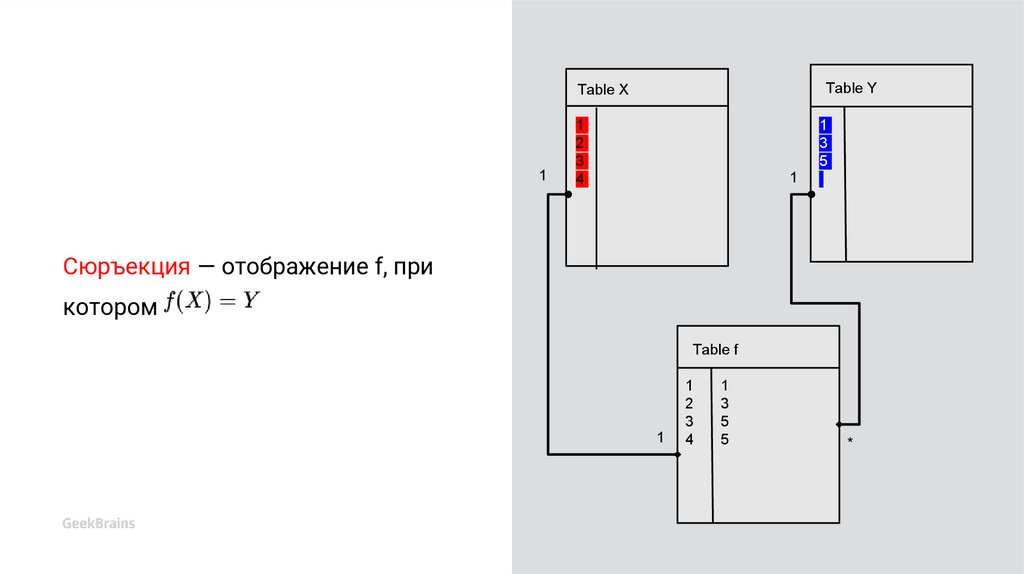
Сюръекция — отображение , прикотором
14.
Table YTable X
1
1
2
3
4
1
3
5
1
Сюръекция — отображение f, при
котором
Table f
1
1
2
3
4
1
3
5
5
*
15.
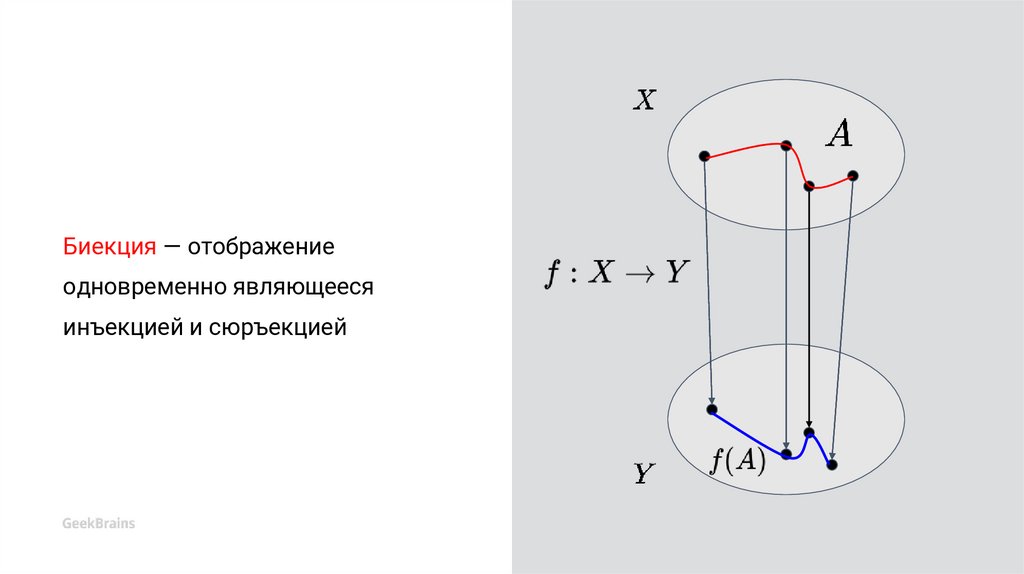
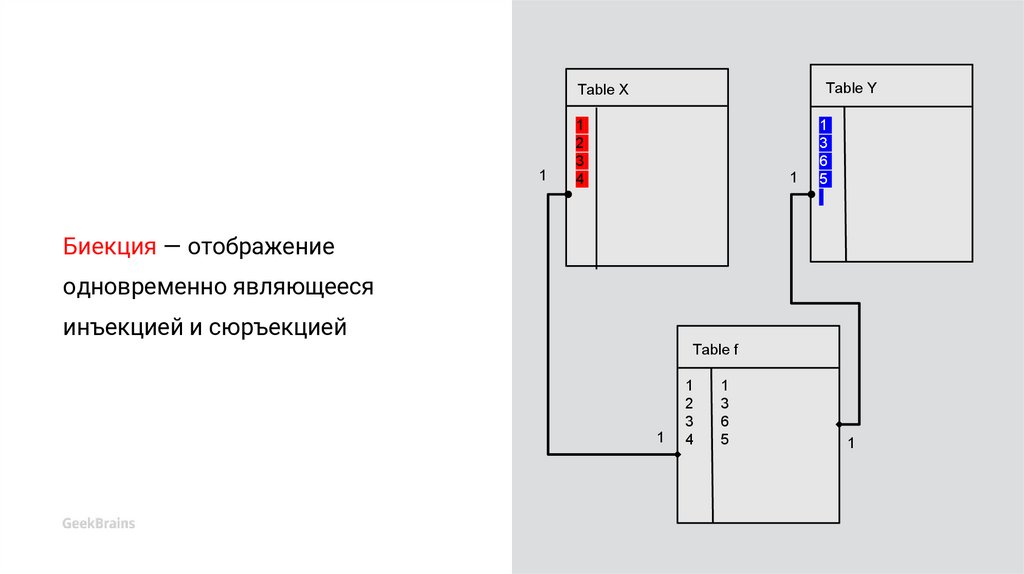
Биекция — отображениеодновременно являющееся
инъекцией и сюръекцией
16.
Table YTable X
1
1
2
3
4
1
1
3
6
5
Биекция — отображение
одновременно являющееся
инъекцией и сюръекцией
Table f
1
1
2
3
4
1
3
6
5
1
17.
1. Сформировано понятие обИтоги
отображении, образе и
прообразе
2. Закреплено понятие о
биекции отображения
18.
Часть 4 Тема 1Функция и ее предел
Определение и свойства функций
19.
1. Понятие об операторе,В этом видео
преобразовании и функции
2. Определения предела
функции
3. Виды пределов
20.
Функцией называется множествоупорядоченных пар
, таких,
что пары существуют для всех
элементов множества , и, если
первые элементы пар совпадают, то
совпадают и вторые их элементы.
21.
1. - область задания (определения) функции2. - область значений функции
3. Множество всех элементов
, называется
множеством значений функции
4. Множество упорядоченных пар
функции
называется также графиком
22.
Оператор - ставит функцию всоответствие другой функции
23.
Преобразование - оператор,изменяющий аргумент функции.
24.
Предел функции (по Коши)25.
Предел функции (по Гейне)26.
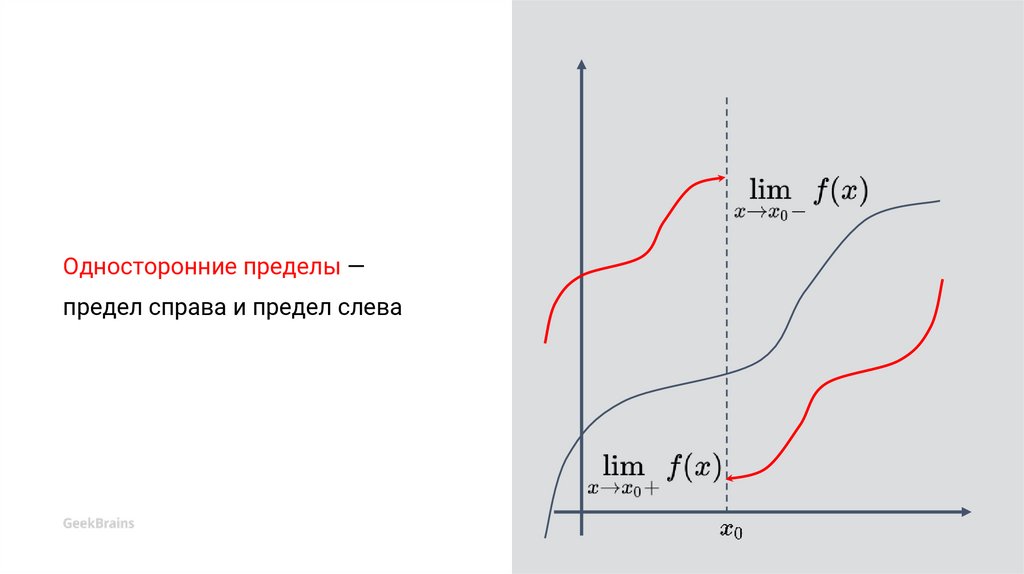
Односторонние пределы —предел справа и предел слева
27.
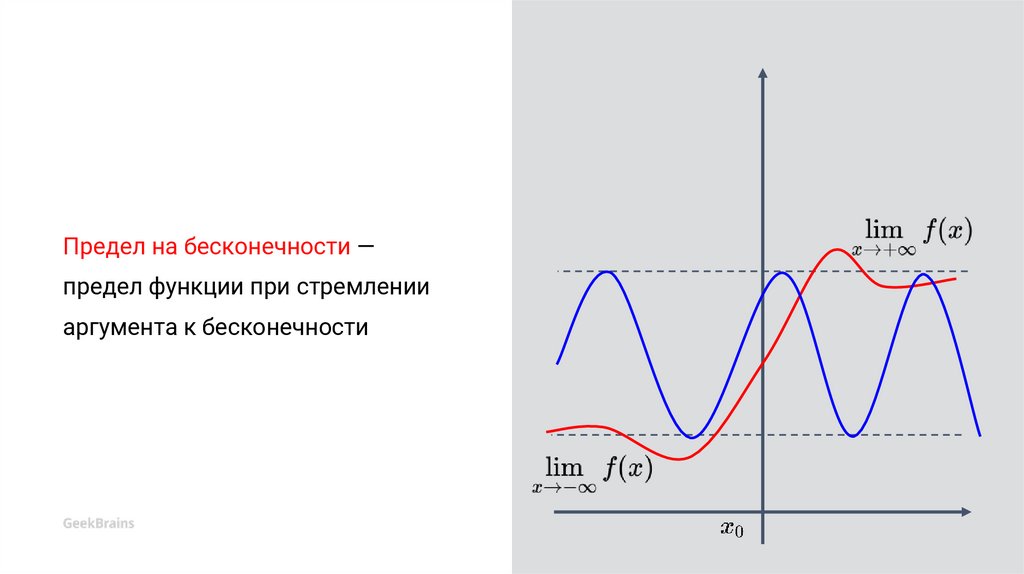
Предел на бесконечности —предел функции при стремлении
аргумента к бесконечности
28.
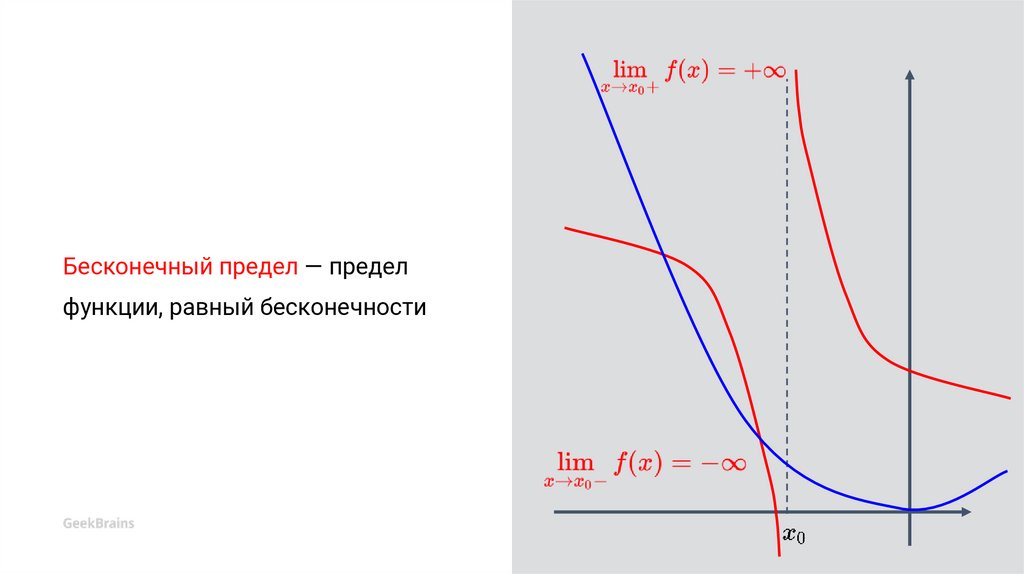
Бесконечный предел — пределфункции, равный бесконечности
29.
Примеры нахождения пределов30.
1. Сформировано определениефункции, отделено от
оператора и преобразования
Итоги
2. Дано два равноправных
определения предела
функции
3. Изучены виды пределов,
разобраны примеры
31.
Часть 4 Тема 3Свойства функции
Математический анализ функции
32.
1. Описания множеств заданияВ этом видео
и значений
2. Особые точки
3. Виды поведения функции
33.
Область задания(область определения)
34.
Примеры35.
Область значений36.
Примеры37.
Нули функции38.
Непрерывность39.
Промежутки знакопостоянства40.
Монотонность1)Убывание на
:
1)Невозрастание на
:
41.
Монотонность3)Неубывание на
:
3)Возрастание на
:
3)Стационарная на
неубывающая на
- невозрастающая и
42.
Четность функцииНечетность функции
43.
Ограниченность функциисверху:
снизу:
44.
Периодичность45.
1. Изучены свойства функций.2. Даны определения
Итоги
непрерывности,
монотонности,
периодичности,
знакопостоянства и
ограниченности функции.























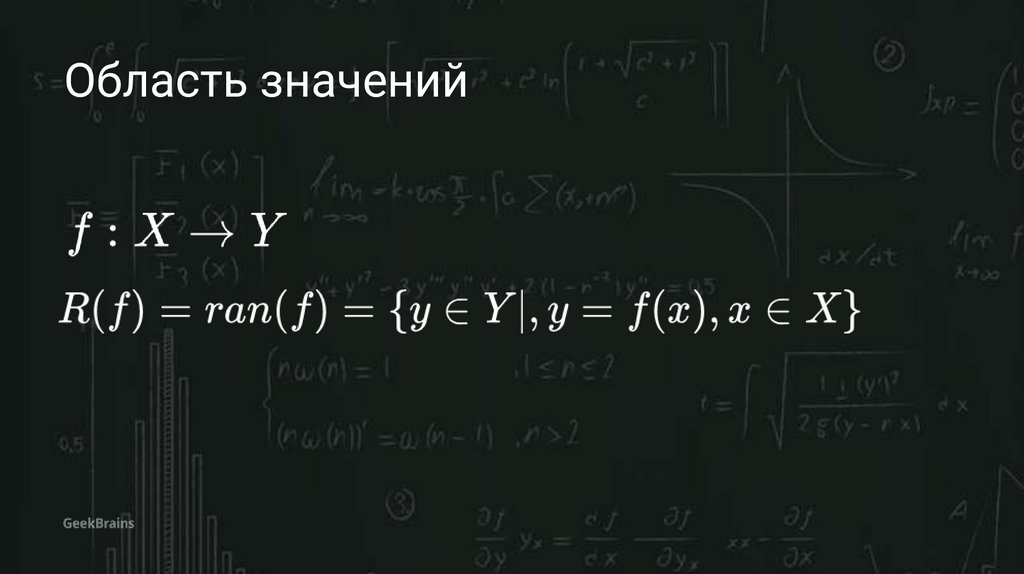

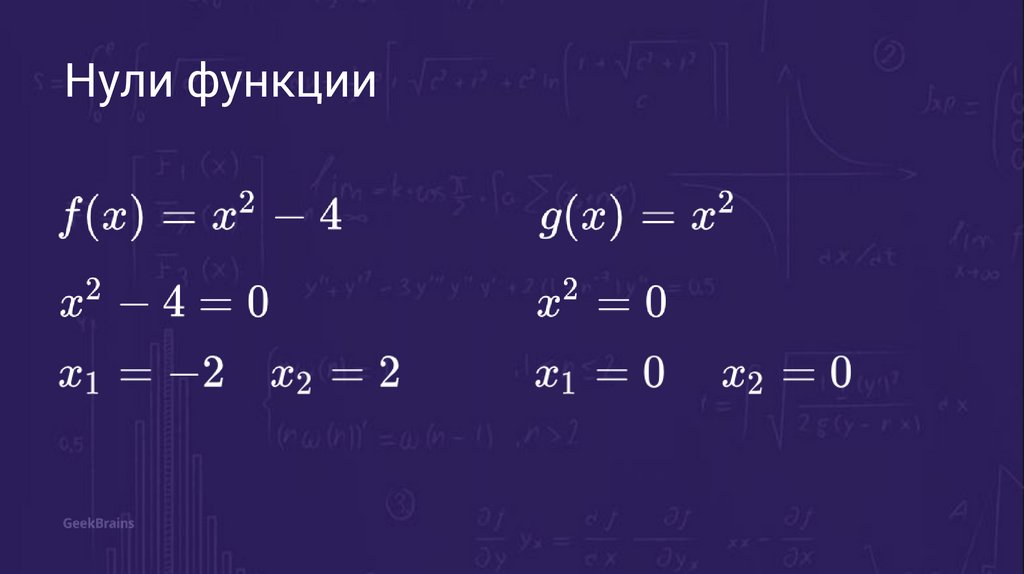






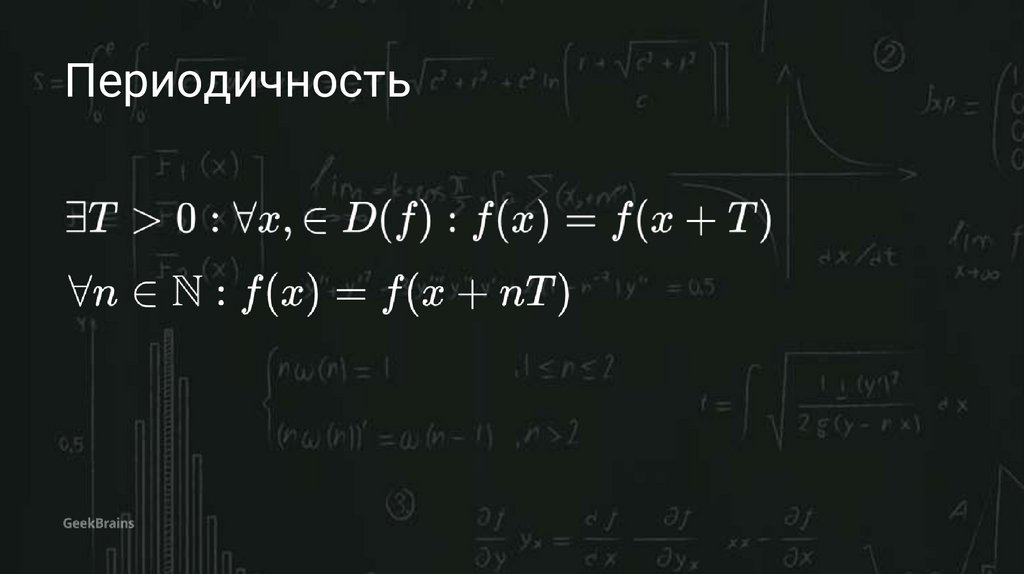

 mathematics
mathematics








