отображения

1. Отображения

Модуль № 3

2. Отображение

Def. Отображением f: Х→У называется такое
соответствие между множествами Х и У, при
котором
каждому элементу х
из Х
соответствует единственный элемент у из У.
Множество Х называется областью определения,
множество У – областью действия,
f – закон соответствия.

3. Условия равенства отображений

При этом элемент y называют образом
элемента х при отображении f, а элемент х –
прообразом элемента у при этом отображении.
Def. Отображения f: Х→У
и g: Х1 →У1
называются равными, если у них совпадают
области определения, области действия и законы
соответствия:
Х = Х 1,
У = У 1,
f(х) = g(х)

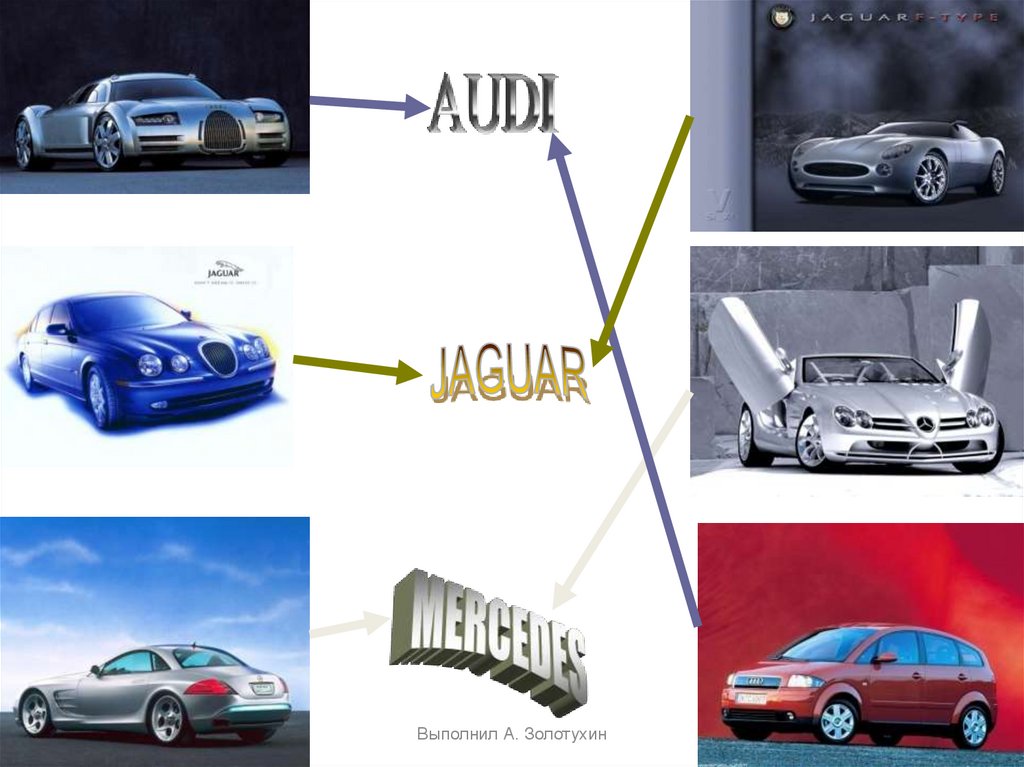
4. Примеры отображений

f: Х→У
Х = {автомобили}
У = {фирмы-изготовители}
f (автомобиль)=фирма, его сделавшая
Выполнил А.Золотухин

5.

Выполнил А. Золотухин

6. Примеры отображений

f: Х→У
Х = {зрители в театре}
У = {кресла в зрительном зале}
f (зритель)=кресло, им занимаемое

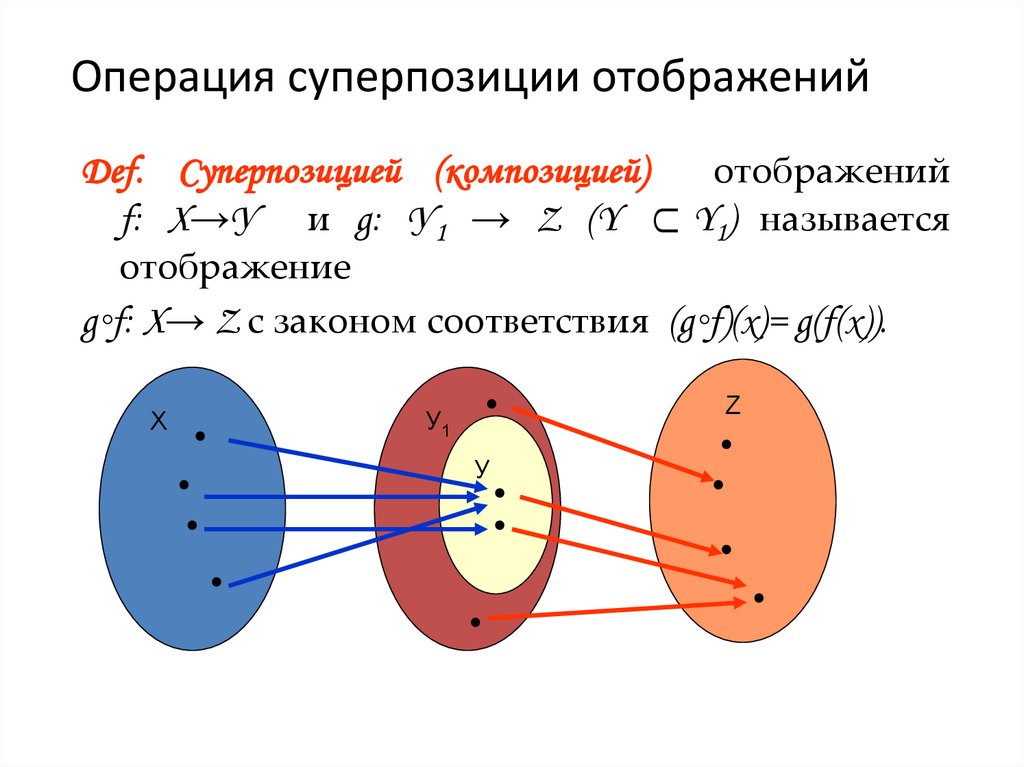
7. Операция суперпозиции отображений

Def. Суперпозицией (композицией)
отображений
f: Х→У и g: У1 → Z (Y Y1) называется
отображение
g◦f: Х→ Z с законом соответствия (g◦f)(х)= g(f(х)).
Х
Z
У1
У

8. Свойства суперпозиции отображений

1. Антикоммутативность
Суперпозиция
отображений
некоммутативна:
g f f g
2. Ассоциативность
Суперпозиция
отображений
ассоциативна: ( g f ) h g ( f h)

9. Виды отображений

def1.
Отображение
называется
инъективным,
если
разным
прообразам соответствуют разные
образы или x1 x2 X f ( x1 ) f ( x2 )
def2.
Отображение
называется
сюръективным, если у каждого
элемента области действия есть
прообраз или y Y x X : y f ( x)

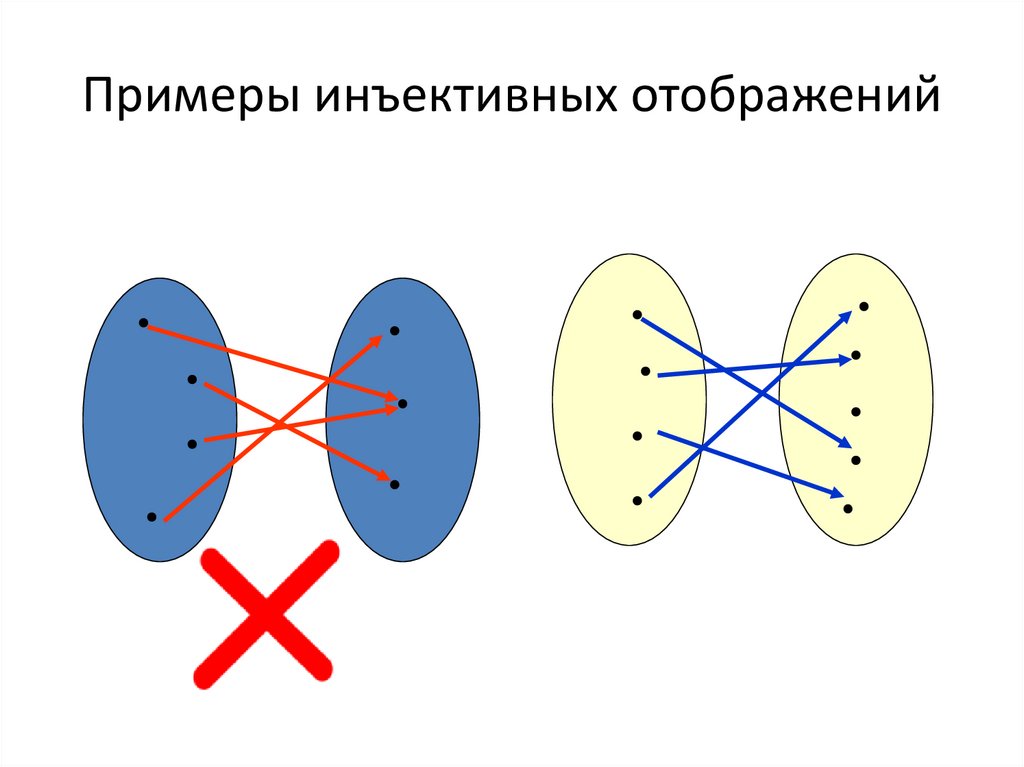
10. Примеры инъективных отображений

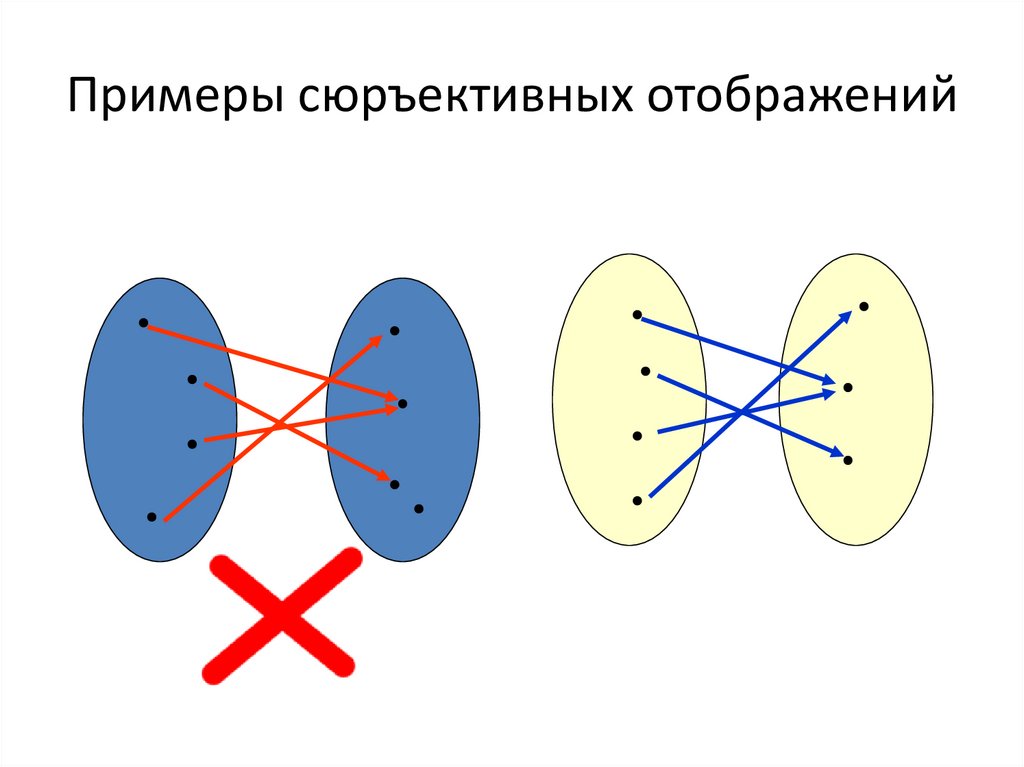
11. Примеры сюръективных отображений

12. Виды отображений

def3. Отображение называется
биективным
или
взаимно
однозначным,
если
оно
инъективно и сюръективно.

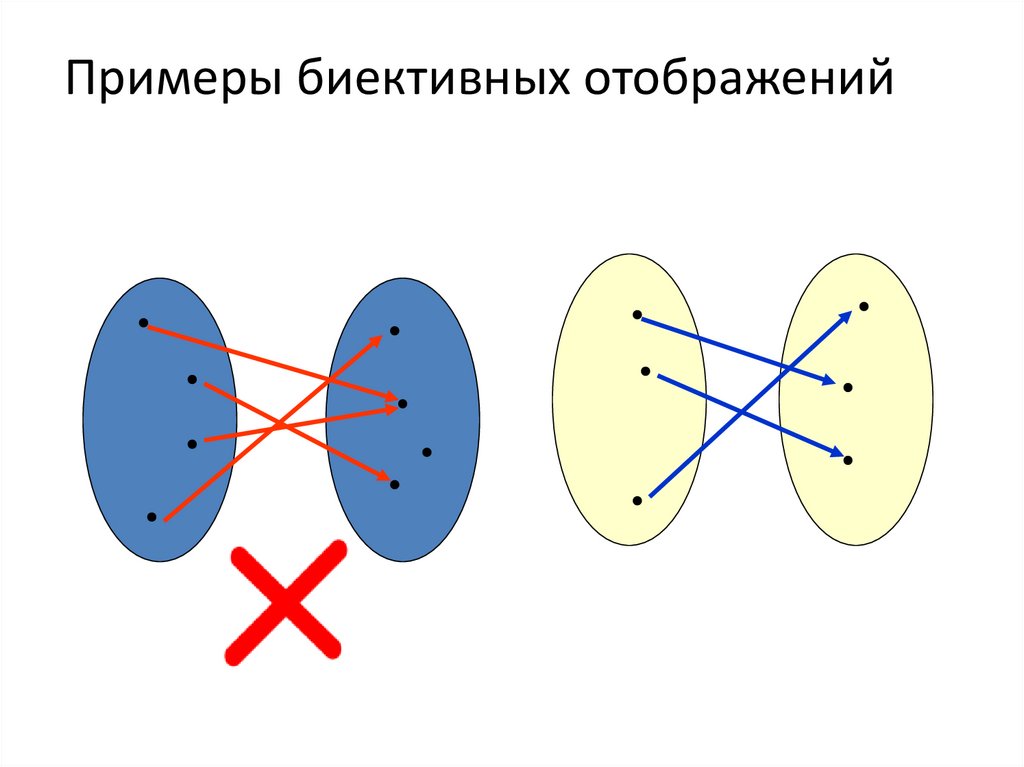
13. Примеры биективных отображений

14.

Примеры биективных отображений

15. Свойства суперпозиции отображений

3. Суперпозиция инъективных отображений
инъективна

16. Свойства суперпозиции отображений

4. Суперпозиция сюръективных
отображений сюръективна

17. Свойства суперпозиции отображений

5. Суперпозиция биективных
отображений биективна
Доказательство следует из свойств 3 º и 4º.

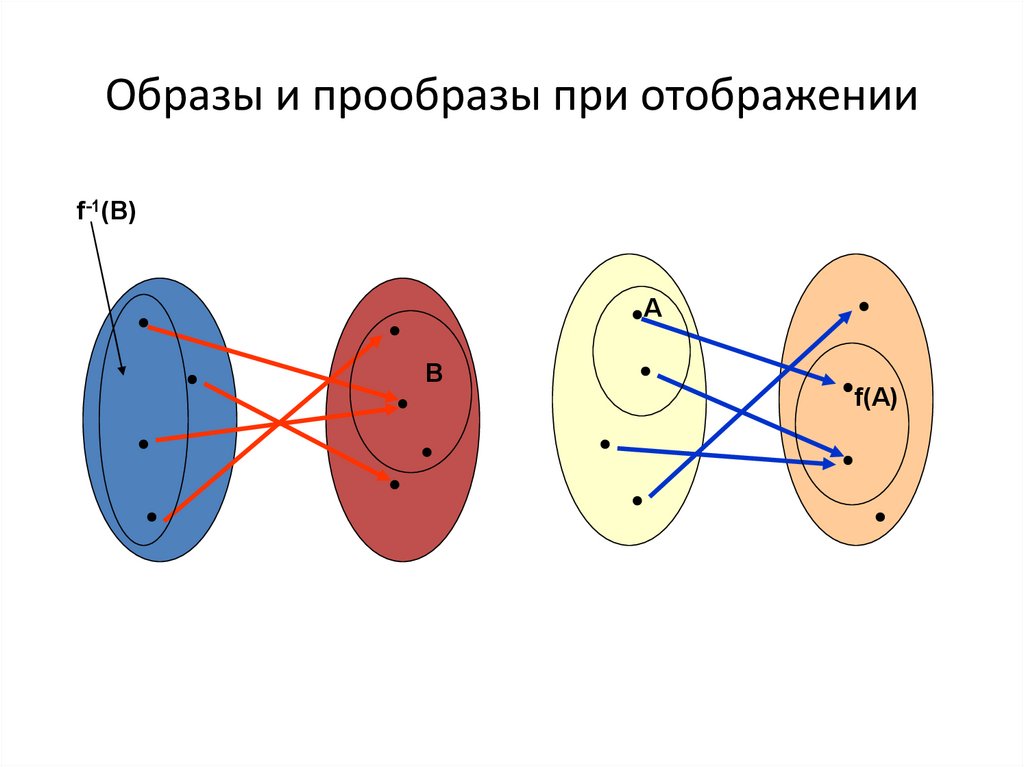
18. Образы и прообразы при отображении

f:Х→Y, А Х, В Y
Dеf1. Прообразом множества В при
отображении f называется множество
f -1(B), определяемое условием:
x f ( B) f ( x) B
1

19. Образы и прообразы при отображении

f:Х→Y, А Х, В Y
Dеf2. Образом множества А при
отображении f называется множество
f (А), определяемое условием:
y f ( A) f
1
y А

20. Образы и прообразы при отображении

f-1(В)
А
В
f(А)

21. Свойства образов и прообразов при отображении

Теорема о свойствах образов и прообразов
при отображении.
1. Образ объединения двух множеств равен
объединению образов этих множеств
f ( A1 A2 ) f ( A1 ) f ( A2 )

22. Свойства образов и прообразов при отображении

Док-во.
y f ( A1 A2 ) f 1 ({ y}) ( A1 A2 )
( f 1 ({ y}) A1 ) f 1 ({ y}) A2 )
f 1 ({ y}) A1 ) или f 1 ({ y}) A2
y f ( A1 ) или y f ( A2 ) y f ( A1 ) f ( A2 ).

23. Свойства образов и прообразов при отображении

2. Прообраз объединения двух множеств
равен объединению прообразов этих
множеств
f
1
( B1 B2 ) f
1
( B1 ) f
1
( B2 )

24. Свойства образов и прообразов при отображении

Док-во.
x f
1
( B1 B2 ) f ( x ) B1 B2
f ( x ) B1 или f ( x ) B2
x f
1
1
( B1) или х f
1
1
x f ( B1 ) f ( B2 ).
( B2 )

25. Свойства образов и прообразов при отображении

3. Образ пересечения двух множеств вложен в
пересечение образов этих множеств
f ( A1 A2 ) f ( A1 ) f ( A2 )

26. Свойства образов и прообразов при отображении

3. Образ пересечения двух множеств вложен в
пересечение образов этих множеств
f ( A1 A2 ) f ( A1 ) f ( A2 )
Док-во.
y f ( A1 A2 ) f
f
1
1
({ y}) ( A1 A2 )
({ y}) A1 и f
1
({ y}) A2
y f ( A1 ) и y f ( A2 ) y f ( A1 ) f ( A2 )

27. Свойства образов и прообразов при отображении

4. Прообраз пересечения двух множеств равен
пересечению прообразов этих множеств
f
1
( B1 B2 ) f
1
( B1 ) f
1
( B2 )
1
Док-во. x f ( B1 B2 ) f ( x) B1 B2
f ( x) B1 и f ( x) B2 x f 1 ( B1 ) и x f 1 ( B2 )
x f
1
( B1 ) f
1
( B2 ).

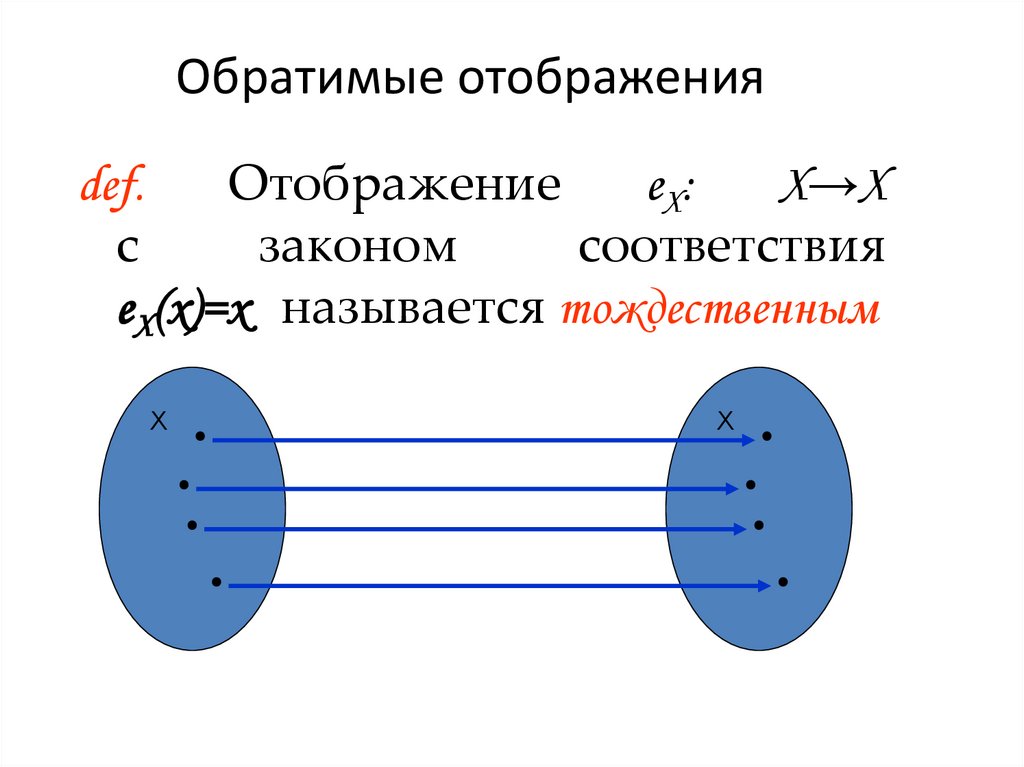
28. Обратимые отображения

def.
Отображение
еХ:
Х→Х
с
законом
соответствия
еХ(х)=х называется тождественным
Х
Х

29. Обратимые отображения

def. Отображение f:Х→У называется
обратимым слева (справа), если
существует
левое
(правое)
обратное отображение :
f : Y X f f eX
1
1
f п : Y X f f п eY
1
л
1
л

30. Обратимые отображения

def. Отображение f: Х→У называется
обратимым или двусторонне обратимым,
если существует обратное
отображение :
f :Y X :
1
f f eX и f f
1
1
eY

31. Критерии обратимости отображений

Теорема 1 (критерий левой обратимости).
Отображение f:Х→У обратимо слева
тогда и только тогда, когда оно
инъективно.
Док-во.

32. Критерии обратимости отображений

33. Критерии обратимости отображений

Теорема
2
(критерий
правой
обратимости). Отображение f: Х→У
обратимо справа тогда и только
тогда, когда оно сюръективно.
Док-во.

34. Критерии обратимости отображений

35. Критерии обратимости отображений

Теорема 3 (критерий двусторонней
обратимости). Отображение f: Х→У
обратимо тогда и только тогда, когда
оно биективно.
Док-во.

36. Критерии обратимости отображений

37. Свойства суперпозиции отображений

6.
Суперпозиция
отображений,
обратимых слева, обратима слева.
7.
Суперпозиция
отображений,
обратимых справа, обратима справа.
8.
Суперпозиция
отображений обратима.
обратимых