Similar presentations:
Математическая статистика. Формула классической вероятности
1.
ТЕОРИЯ ВЕРОЯТНОСТЕЙИ
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
2.
Лекция 33. Формула классической вероятности
mP ( A)
n
,
где
m – число элементарных исходов,
благоприятствующих А;
n – число всех возможных
элементарных исходов испытания.
Элементарные исходы несовместны,
равновозможны и образуют полную
группу.
4. Свойства вероятности
Свойство 1. Вероятностьдостоверного события равна
единице.
m n
Р( А) 1
n n
5.
Свойство 2. Вероятностьневозможного события равна
нулю.
m 0
Р( А) 0
n n
6.
Свойство 3. Вероятностьслучайного события А есть число,
заключенное между нулем и
единицей.
m
0 P( A) 1.
n
7. Требования к классической схеме
1) Выбрать множество элементарныхисходов
2)Подсчитать число всех элементарных
исходов
3)Если вычисляем P(A), подсчитать
число благоприятных исходов.
8. Пример 1
Монету подбрасывают дважды.Построить множество
элементарных исходов.
9. Решение
Если учитывать порядок, то исходовполучится четыре
(герб,герб) (решка,решка) (герб,решка)
(решка,герб)
Все эти исходы равновозможны.
10.
Если порядок не учитывать, то исходы(решка,герб) и (герб,решка) считают
как один. Тогда элементарных исходов
будет три
(герб,герб) (решка,решка) (герб,решка)
11.
Гипергеометрическаяформула
12. В случае разбиения исходного множества на два подмножества
C CP A
n
CN
m
M
n m
N M
13.
P AC
m
M
C
n
CN
n m
N M
N – общее количество элементов
M – количество элементов
определенного типа
n – отобранные
m – количество элементов в выборке,
связанных с M
14.
Пример 1В фирме работают 6 женщин и 4 мужчин.
Наудачу отобраны 7 человек. Чему равна
вероятность, что среди отобранных ровно
3 женщины?
Решение:
Тогда
Имеем N=10; n=7; M=6; m=3.
3
6
4
4
CC
1
P( A) 7
C10
6
15.
Пример 2В партии из 6 деталей 3 стандартных.
Найти вероятность того, что среди
четырех взятых наудачу деталей 2
стандартных.
Решение: Имеем N=6; n=4; M=3;
m=2.
2 2
Тогда
3 3
4
6
C C
3
P( A)
C
5
16. Покерные комбинации
Пара(2) :Т♠;10♣;К♣;2♦;2♠Две пары:(2+2) 10♠;10♣;К♣;2♦;2♠
Тройка(3): Т♠;10♣;2♣;2♦;2♠
Стрит(Street): Т♠;10♣;К♣;Д♦;В♥
Флеш(Flush): Т♠;10 ♠;К ♠;2 ♠;2♠
3+2: 10♠;10♣;2♣;2♦;2♠
Каре: 10♠; 2♥;2♣;2♦;2♠
S+F: Т♣;10♣;К♣;Д♣;В♣.
17. Расчет вероятностей покерных комбинаций
Результат эксперимента – наименованияпяти карт, например, (Т♠;10♣;К♣;2♦;2♠).
Число всех исходов
n C 2 598 960
5
52
18. Вероятность пары
Число благоприятных исходов и вероятностьпары
m C C C C C C 1098240
1
13
2
4
3
12
1
4
1
4
1
4
m
P "2" 0,4225690276
n
19. Вероятность двух пар
Число благоприятных исходов и вероятностьдвух пар
m C C C C C 494208
2
13
2
4
2
4
1
11
1
4
m
P "2 2" 0,1901560624
n
20.
C131 C43 C122 C41 Ñ4154912
P "3"
=0,0211284514
2598960
2598960
9 C41 C41 C41 Ñ41 C41
9216
P " S "
=0,0035460338
2598960
2598960
C135 Ñ41
5148
P " F "
=0,0019807923
2598960 2598960
C131 C43 C121 C42
3744
P "3 2"
=0,0014405762
2598960
2598960
1
1
1
C13 Ñ12 C4
624
P " K "
=0,0002400960
2598960
2598960
9 4
36
P " S F "
=0,0000138517
2598960 2598960
21. Относительная частота
Относительной частотой событияназывают отношение числа испытаний,
в которых событие появилось, к общему
числу фактически произведенных
испытаний.
m
W ( A)
n
где m – число появлений события,
n – общее число испытаний.
22.
ПримерПо цели произвели 32 выстрела,
причем было зарегистрировано 15
попаданий. Чему равна относительная
частота поражения цели?
Решение: общее число испытаний
n=32.
Событие появилось 15 раз, то есть
m=15. Тогда W(A)=15/32.
23.
Статистическая вероятностьпоявления события
Относительная частота –
приближенное значение
вероятности, называемое
статистической.
24. Пример
По данным статистики,относительная частота
рождения девочек за
некоторый год по
месяцам характеризуется
следующими числами
(начиная с января):
0,486; 0,489; 0,490; 0,471; 0,478; 0,482;
0,462; 0,484; 0,485; 0,491; 0,482; 0,473.
25.
Относительная частотаколеблется около числа 0,482,
которое можно принять за
приближенное значение
вероятности рождения девочек.
26. Проверка свойств статистической вероятности
1. Если событие достоверно, тоm = n и относительная частота
m
n
1
n
n
2. Если событие невозможно, то
m = 0 и, следовательно,
0
относительная частота
n
0
27.
Для любого события 0 m n ,и, следовательно, относительная
частота
m
0 1 ,
n
т.е. статистическая вероятность
любого события заключена между
нулем и единицей.
28. Операции над событиями
29. Сумма событий
Пусть даны события А и В.Сумма событий А+В – событие,
которое означает, что произошло хотя
бы одно из исходных событий.
30. Разность событий
Разностью двух событий A-Bназывается событие, состоящее в
том, что А произошло, но В не
произошло
31. Произведение событий
Пусть даны события А и В.Произведение событий АВ – событие,
которое означает, что одновременно
произошли оба события.
32. Противоположные события и
Противоположные событияA
и
A
События называются
противоположными, если они
несовместны и образуют полную
группу.
p( A) p( A) 1
33.
Другими словами:Событием, противоположным к А,
называется событие Ā, состоящее в
том, что событие А не произошло.
34. Примеры
А={идет дождь}В={идет снег}
АВ={идет дождь и снег}
А+В={идет дождь или снег}
35. Пример противоположного события
A= {попадание в мишень}
A
= {промах}
36.
Задача 1Вероятность того, что день будет ясным равна
0,3. Чему равна вероятность, что день будет
дождливым?
Решение.
A
={день ясный}
A
={день дождливый}
Так как сумма противоположных событий
равна 1, то вероятность, что день будет
дождливым равна 1- 0,3 = 0,7.
37. Задача 2
Вероятность не сдать зачет попредмету для некоторого студента
равна 0,8. Какова вероятность
сдать зачет?
38. Решение
Обозначим событие A={сдать зачет}.Тогда противоположным событием
будет событие Ā={не сдать зачет}.
Так как P(A)+P(Ā)=1, то P(A)=1-P(Ā)
Вероятность P(A)=1-0,8=0,2
39. Вероятностное пространство
40.
Пусть в результате испытаниянаступает одно и только одно из
совокупности событий, называемых
элементарными событиями
(элементарными исходами):
i , (i 1,2,..., n,...)
41.
Множество всех элементарныхсобытий, которые могут
появиться в испытании, называют
пространством элементарных
событий ,
а сами элементарные события –
точками пространства .
42. Пример
В урне 4 шара: красный, синий, желтый,зеленый. Наудачу вынимают один шар.
Выпишем множество элементарных исходов
1
2
3
4
- вынули красный шар
- вынули синий шар
- вынули желтый шар
- вынули зеленый шар
43.
Пространство{ 1 , 2 , 3 , 4 }
Точки этого пространства
1 , 2 , 3 , 4
44. Поле событий S
Поле событий – подмножествомножества всех подмножеств ,
замкнутое относительно операций
объединения, пересечения,
дополнения, содержащее само и
пустое подмножество.
45. Аксиомы вероятностного пространства:
1. Каждому событию А поставлено всоответствие неотрицательное
действительное число Р (А). Это число
называется вероятностью события А;
2. Вероятность достоверного события
равна единице: Р ( ) 1 ;
3. Вероятность наступления суммы
попарно несовместных событий равна
сумме вероятностей этих событий.
46. Вероятностное пространство
, S , p47. Типы пространств
Выделяют два основных типа:Дискретное вероятностное
пространство;
Непрерывное вероятностное
пространство.
48. Дискретное вероятностное пространство
Конечное –классическая схема;
неклассическая.
Бесконечное.
49. Непрерывное пространство
Пример.Случайный эксперимент – измерение
роста человека. Случайное событие –
произвольное положительное
действительное число.
50. Геометрические вероятности
Геометрические вероятности –вероятности попадания точки в
область (отрезок, часть плоскости и
т.д.).
51.
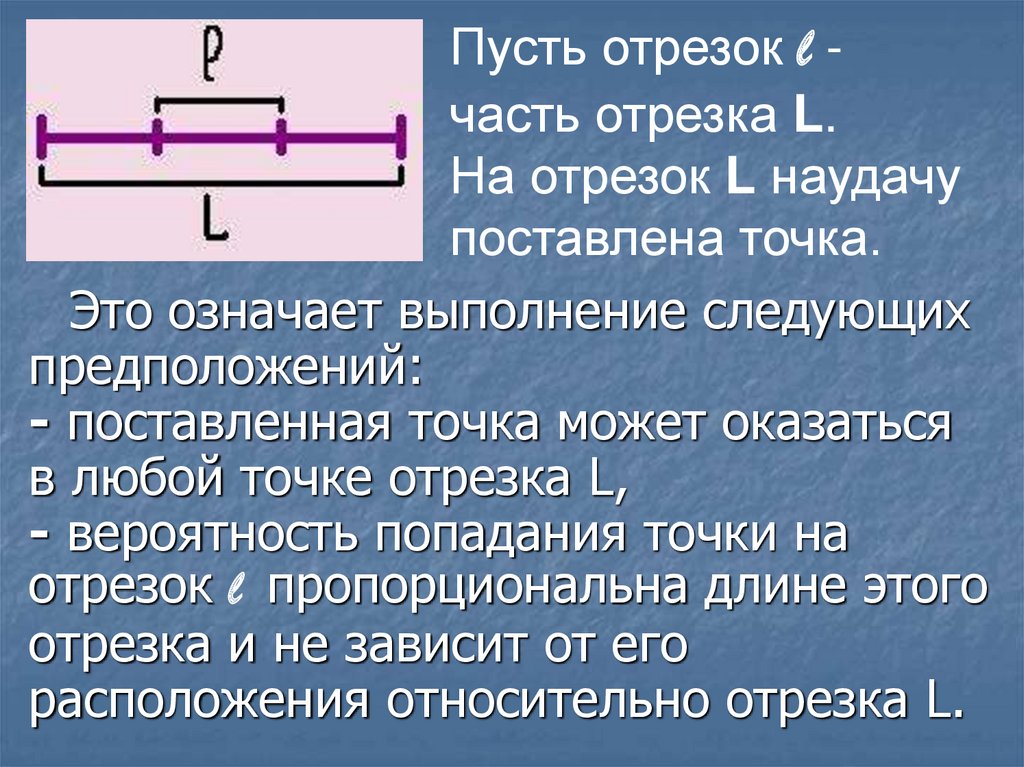
Пусть отрезок l часть отрезка L.На отрезок L наудачу
поставлена точка.
Это означает выполнение следующих
предположений:
- поставленная точка может оказаться
в любой точке отрезка L,
- вероятность попадания точки на
отрезок l пропорциональна длине этого
отрезка и не зависит от его
расположения относительно отрезка L.
52.
Вероятность попаданияточки на отрезок l определяется
равенством
Длина l
P
Длина L
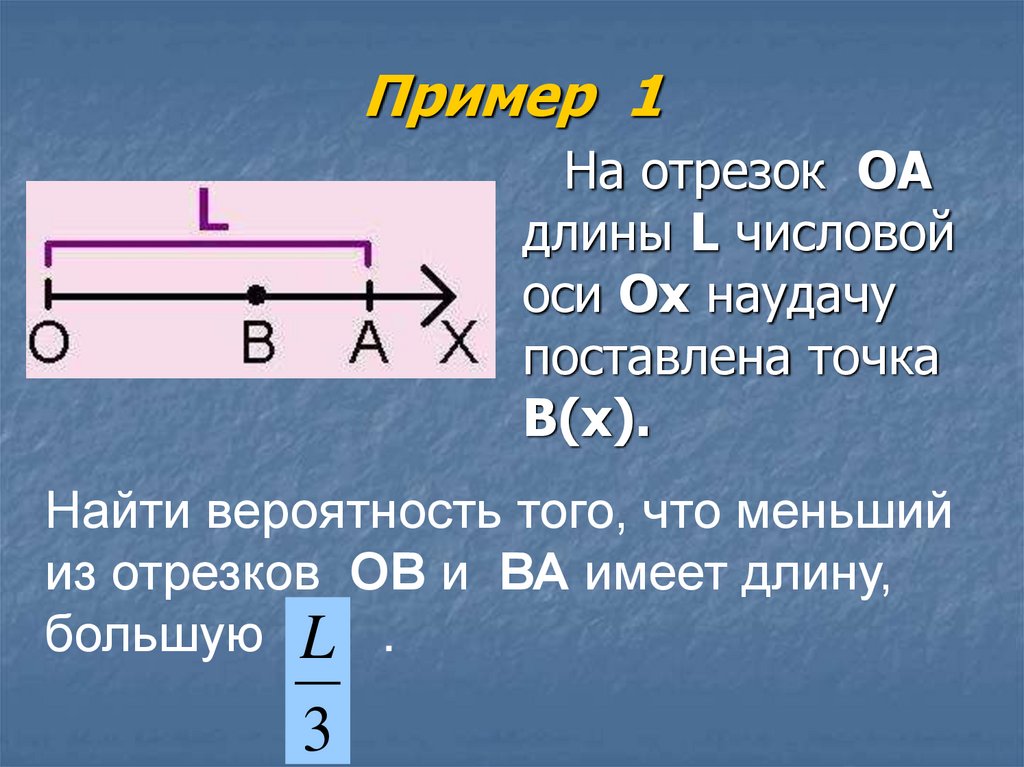
53. Пример 1
На отрезок ОАдлины L числовой
оси Ох наудачу
поставлена точка
В(х).
Найти вероятность того, что меньший
из отрезков ОВ и ВА имеет длину,
большую L .
3
54.
Решение.Разобьем
отрезок ОА
точками С и D
на 3 равных
части.
55.
Требование задачи будетвыполнено, если точка В(х) попадет
на отрезок CD длины L .
3
Искомая
вероятность:
L
1
3
P
.
L
3
56. Пусть плоская фигура g составляет часть плоской фигуры G.
На фигуру G наудачу брошенаточка.
57.
Вероятность попадания точки вфигуру g определяется равенством:
Площадь g
P
Площадь G
58. Пример 2 На плоскости начерчены две концентрические окружности, радиусы
которых 5 и 10 см соответственно.Найти вероятность того, что точка,
брошенная наудачу в большой круг,
попадет в кольцо, образованное
построенными окружностями.
59.
Решение.Площадь кольца (фигуры g):
Sg 10 5 75
2
2
60.
Площадь большого круга(фигуры G):
S G 10 100
2
Искомая вероятность:
75
P
0,75
100
61.
ЗамечаниеВ случае классического определения
вероятность достоверного (невозможного)
события равна единице (нулю);
справедливы и обратные утверждения
(например, если вероятность события равна
нулю, то событие невозможно).
В случае геометрического
определения вероятности
обратные утверждения не имеют
места.
62. Задача о встрече
Два человека договорились встретитсяв течение часа, причем время ожидания
первым относительно второго не
превышает 15 минут. Найти
вероятность их встречи.
63.
Решение.Обозначим моменты прихода
первого и второго соответственно
через x и y. В силу условия задачи
должны выполняться двойные
неравенства:
0 х 1, 0 y 1.
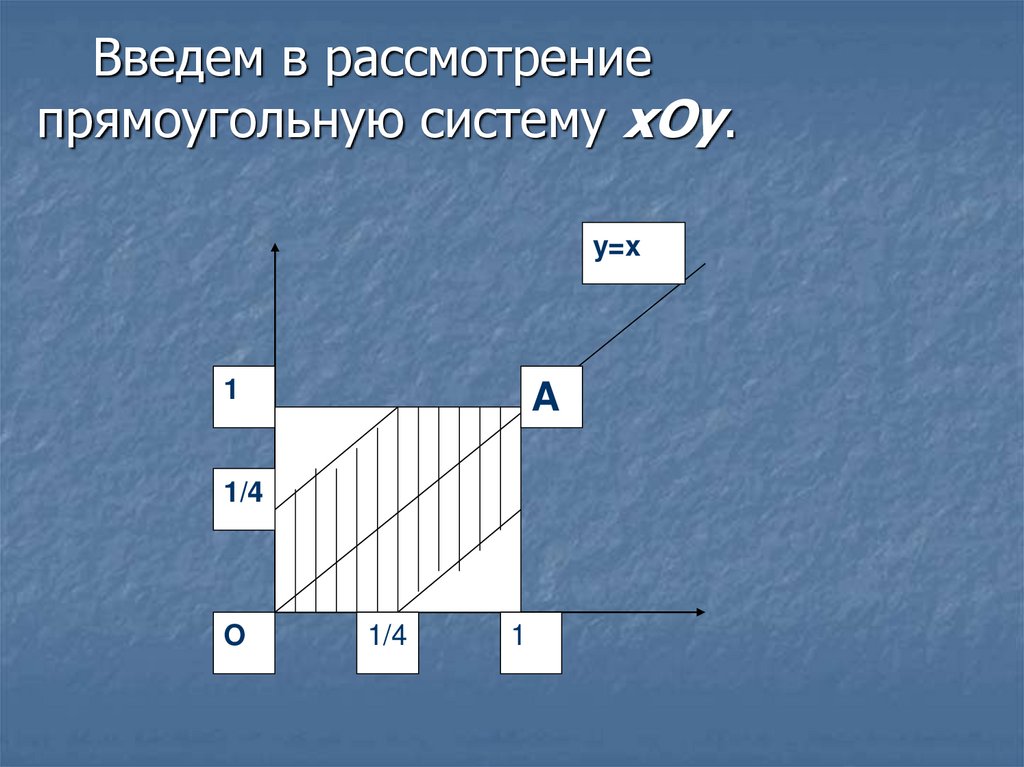
64.
Введем в рассмотрениепрямоугольную систему xOy.
y=x
1
A
1/4
O
1/4
1
65. Таким образом,
23
1
Sg
7
4
P
SG
1
16
66.
Задачи67. Задача 1
В прямоугольник 5x4 см2 вписан круградиуса 1,5 см. Какова вероятность
того, что точка, случайным образом
поставленная в прямоугольник,
окажется внутри круга?
68. Решение
По определению геометрическойвероятности искомая вероятность
равна отношению площади круга (в
который точка должна попасть) к
площади прямоугольника, то есть
1,5
P( A)
0,353
5 4
2
69. Задача 2
В квадрат со стороной 6 вписан круг.Наудачу в квадрат бросают точку.
Найти вероятность, что точка попадет в
круг.
70. Решение
По определению геометрическойвероятности искомая вероятность равна
отношению площади квадрата к
площади круга
Площадь квадрата со стороной 6 равна
S=36
71.
Заметим, что радиус вписанного в квадраткруга будет равен половине стороны
квадрата, R=3
Площадь круга с радиусом R=3 равна
S R 3 9
2
2
Тогда вероятность
9
P ( A)
36 4
72. Вопросы к лекции 3
Напишите гипергеометричекуюформулу
Что называют относительной частотой?
Что такое статистическая вероятность?
Сумма событий
Произведение событий
Противоположные события. Пример
Формула вычисления геометрической
вероятности






































































 mathematics
mathematics








