Применение производной. Демонстрационный материал

1. Применение производной

Демонстрационный материал

2. Возрастание функции

y
y=f(x)
Если f (x)>0 на
промежутке, то функция
возрастает на этом
промежутке
0 а
x
b

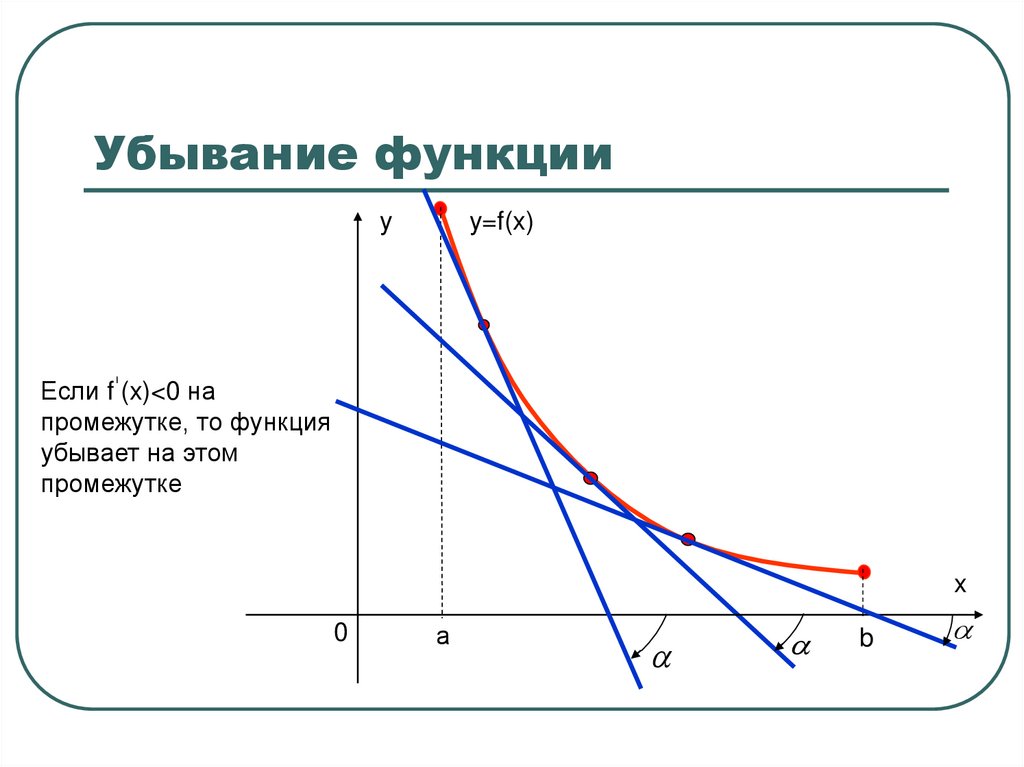
3. Убывание функции

y
y=f(x)
Если f (x)<0 на
промежутке, то функция
убывает на этом
промежутке
x
0
а
b

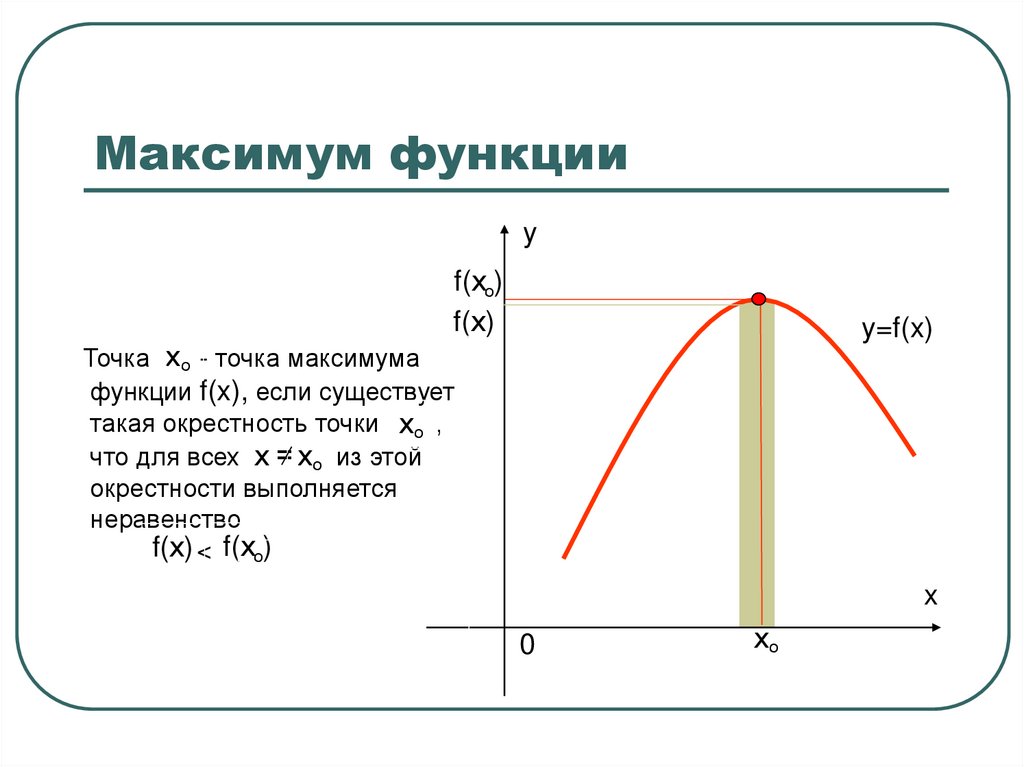
4. Максимум функции

y
f(хо)
f(х)
y=f(x)
Точка х о - точка максимума
функции f(x), если существует
такая окрестность точки х о ,
что для всех х = х о из этой
окрестности выполняется
неравенство
f(х) < f(хо)
x
0
хо

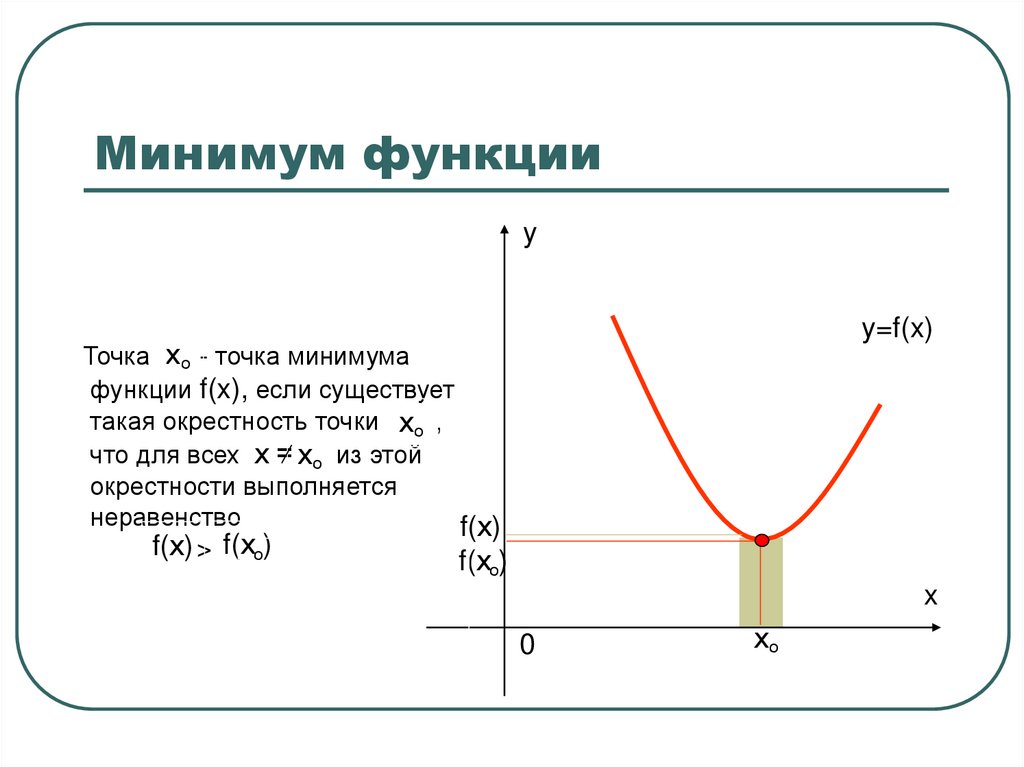
5. Минимум функции

y
y=f(x)
Точка х о - точка минимума
функции f(x), если существует
такая окрестность точки х о ,
что для всех х = х о из этой
окрестности выполняется
неравенство
f(х)
f(х) > f(хо)
f(хо)
x
0
хо

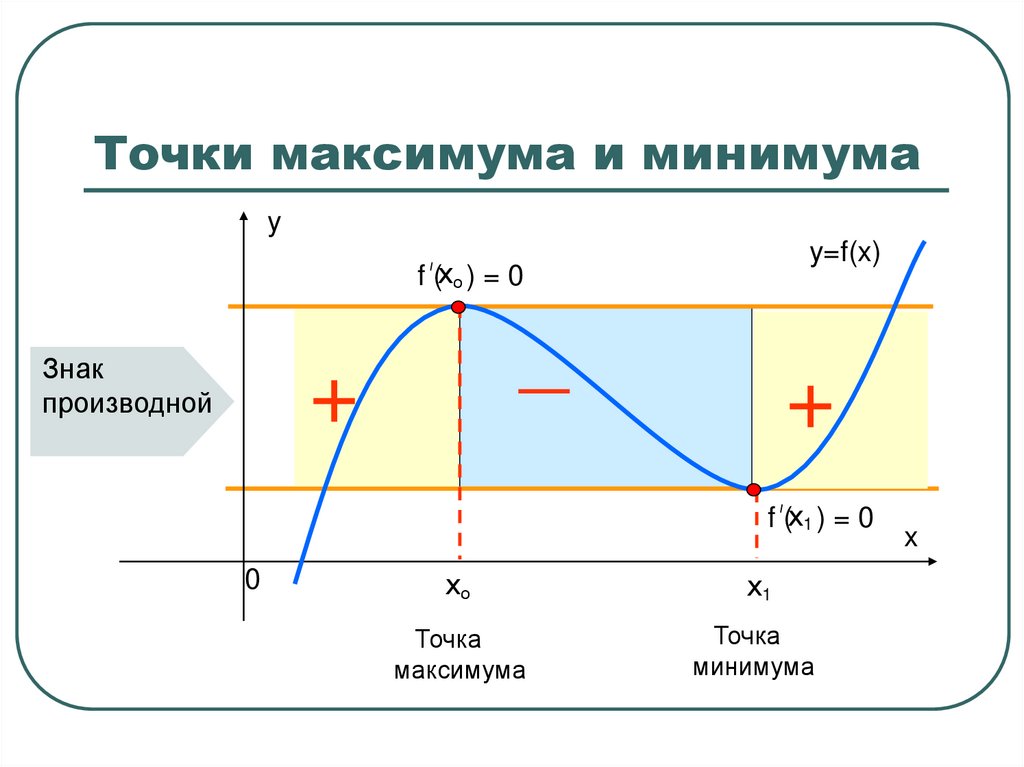
6. Точки максимума и минимума

y
y=f(x)
f (хо ) = 0
Знак
производной
_
+
+
f (х1 ) = 0
0
хо
х1
Точка
максимума
Точка
минимума
x

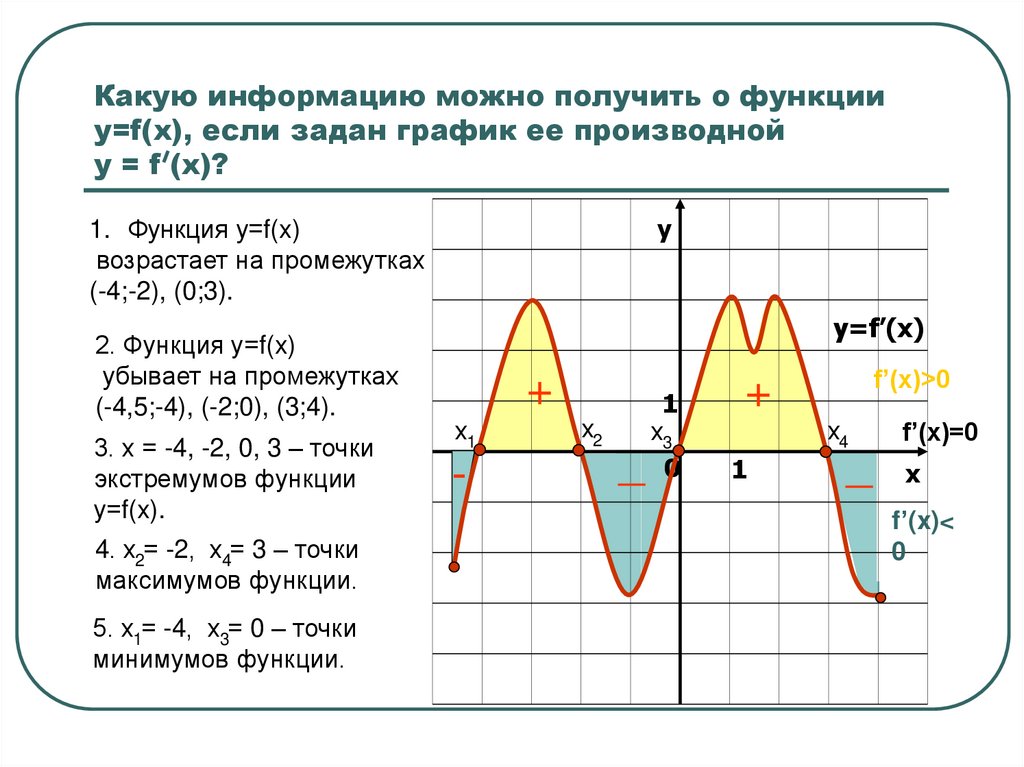
7. Какую информацию можно получить о функции у=f(x), если задан график ее производной у = f (x)?

у
1. Функция у=f(x)
возрастает на промежутках
(-4;-2), (0;3).
2. Функция у=f(x)
убывает на промежутках
(-4,5;-4), (-2;0), (3;4).
3. х = -4, -2, 0, 3 – точки
экстремумов функции
у=f(x).
4. х2= -2, х4= 3 – точки
максимумов функции.
5. х1= -4, х3= 0 – точки
минимумов функции.
y=f’(x)
+
х1
-
х2
_
1
х3
0
f’(x)>0
+
х4
1
_
f’(x)=0
х
f’(x)<
0