Similar presentations:
Геометрический смысл производной
1.
Повторение2. Геометрический смысл производной.
Повторение Геометрический смыслпроизводной.
Производная функции в точке x0 равна
угловому коэффициенту касательной к
графику функции y = f(x) в этой точке.
f x0 tg k
3.
В точке х2 угол наклонакасательной – острый,
значит,
k 0 f ( x2 ) 0
В точке х4 угол
наклона касательной –
тупой, значит,
у
k 0 f ( x4 ) 0
х
х2 х3
х4
В точке х3 угол
наклона касательной –
равен 0°, значит,
k 0, касательная
параллельна оси ОХ
f ( x3 ) 0
4.
Экстремальные точки.Локальный экстремум
функции
5. Окрестность точки
ОпределениеОкрестностью
точки называется некоторый
интервал, содержащий данную
точку
6.
Например:y
-1
О
1
x
у = f(х)
Точка
О є (-1; 1)
Интервал
(-1; 1) –
окрестность точки О.
7. Точка локального максимума
Точка а из области определенияфункции f(х) называется точкой
локального максимума этой функции,
если существует такая окрестность
точки а, что для любого х не равного
а из этой окрестности выполняется:
f(а) > f(х).
8.
y-1
О
1
x
у = f(х)
Пусть т. О є (-1; 1)
Для любого х из
окрестности точки О:
f(0) > f(х)
f(0) – максимальное
значение функции на
данном промежутке, т.е.
х = 0 – точка локального
максимума.
9. Точка локального минимума
Точка а из области определенияфункции f(х) называется точкой
локального минимума этой
функции, если существует такая
окрестность точки а, что для
любого х не равного а из этой
окрестности выполняется:
f(а) ˂ f(х).
10.
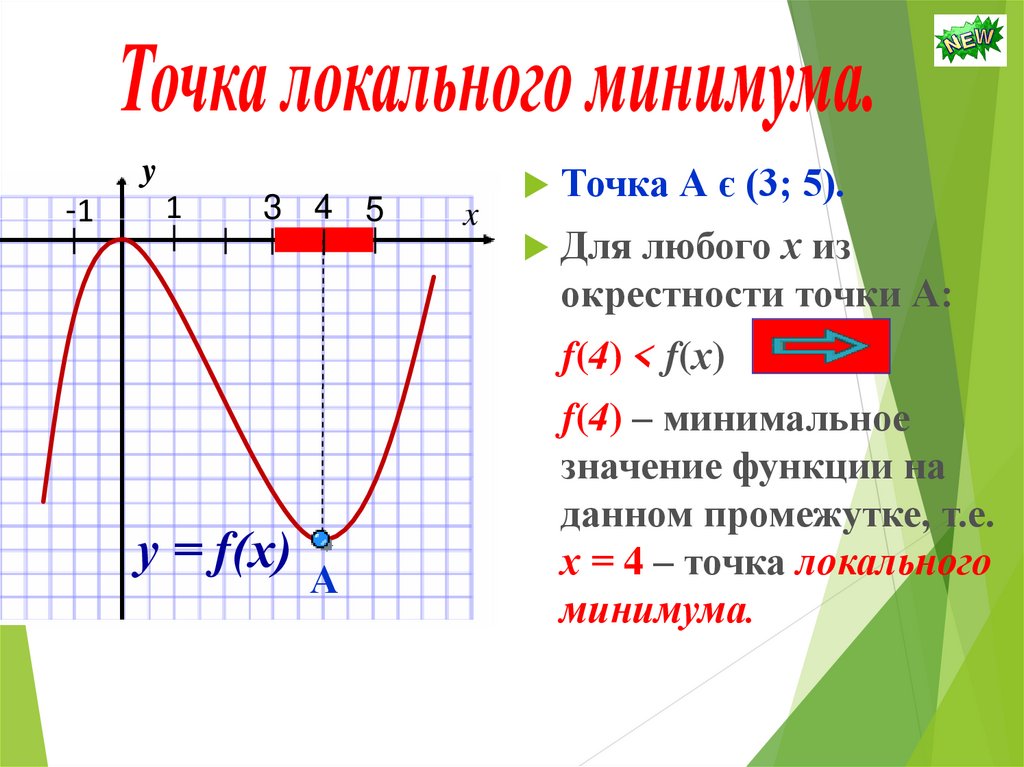
y-1
1
3 4 5
x
Точка А є (3; 5).
Для любого х из
окрестности точки А:
f(4) < f(х)
у = f(х)
А
f(4) – минимальное
значение функции на
данном промежутке, т.е.
х = 4 – точка локального
минимума.
11.
Точкимаксимума и минимума
обозначают:
Хmax, Xmin – точки экстремума.
Значения функции в этих точках
обозначают:
Ymax,
Y min
и называют - экстремумы
функции
12.
13.
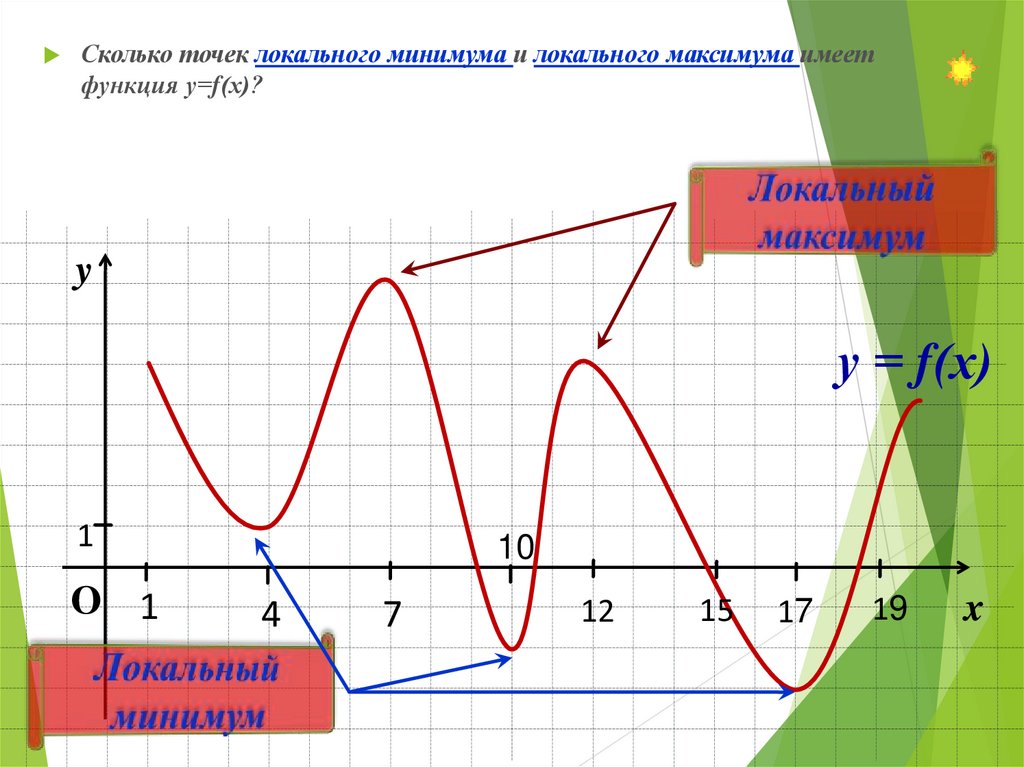
Сколько точек локального минимума и локального максимума имеетфункция у=f(х)?
y
у = f(х)
1
O 1
10
4
7
12
15
17
19
x
14.
1.Сколько точек минимума имеет функция,заданная графиком на отрезке 6;7 ?
Ответ: 2
1) 4
2)3
3)1
4) 2
15.
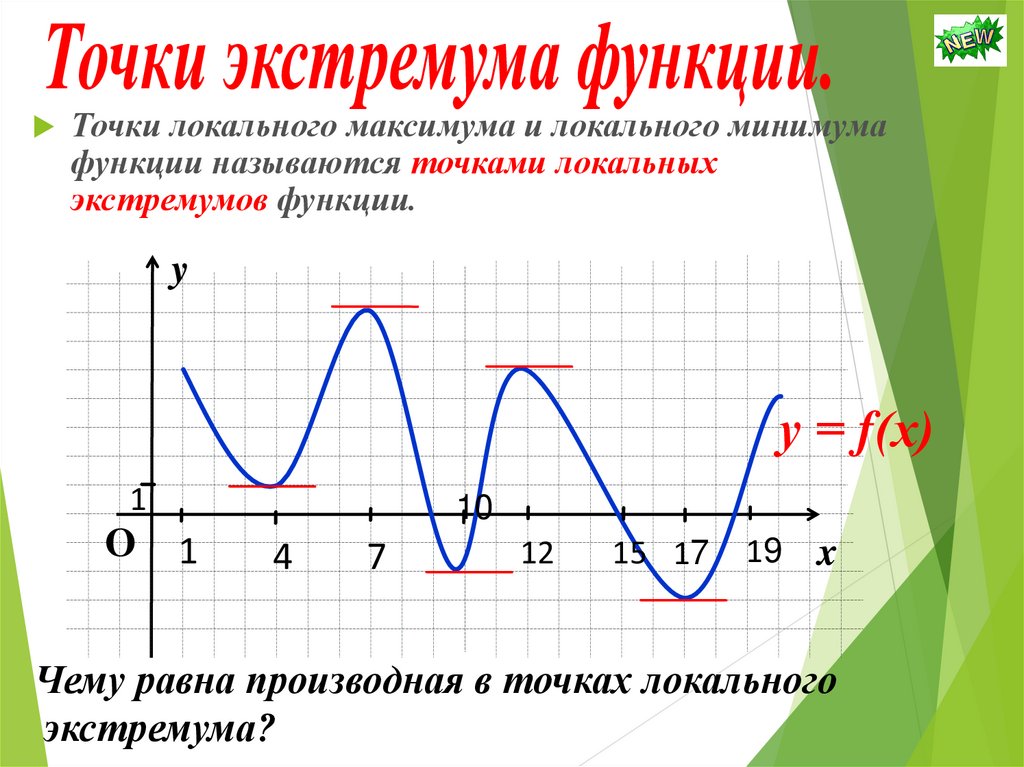
Точки локального максимума и локального минимумафункции называются точками локальных
экстремумов функции.
y
у = f(х)
1
O
10
1
4
7
12
15 17
19
x
Чему равна производная в точках локального
экстремума?
16. Теорема Ферма. (Необходимое условие экстремума)
Теорема. Еслих0 - точка экстремума
дифференцируемой функции f(х), то f ´(х0) = 0.
Геометрический смысл.
y
f´(х1) = 0
x1
у = f(х)
x2
x
f´(х2) = 0
17. Вспомним, что точки, в которых f´(х) = 0 называются критическими или стационарными точками. Данное определение необходимо
дополнить.Внутренние точки области
определения функции, в которых
ее производная равна нулю или
не существует, называются
критическими точками.
18. Ответим на вопрос - верно ли обратное утверждение:
Ответим на вопрос верно ли обратное утверждение:если
функция
дифференцируема в точке х0 и
f ´(х0) = 0 , то следует ли , что
х0 - точка экстремума?
19. Интересно: f ´(х0) = 0 х0 - точка экстремума
х3f (х) =
f ´(х) = 3х2
3х2 = 0; х = 0 –критическая точка,
т.е. f ´(0) = 0,
однако точка х = 0 не есть точка максимума или
точка минимума (обоснуйте, используя
определение)
Значит, х = 0 – не является точкой экстремума.
Видим, что не все критические
точки есть точки экстремума
f (х)= х3
20.
Таким образом, если f' (х0 ) = 0, тонеобязательно, что точка х0 будет
точкой экстремума.
Примеры
21.
Достаточное условие существованияэкстремума функции:
Если при переходе через точку х0
производная от функция меняет знак с
«плюса» на «минус», то точка х0
является точкой максимума.
y
_ _ _
f ( x ) 0
f ( x ) 0
а
х0
f ( x0 ) 0
b
х
22.
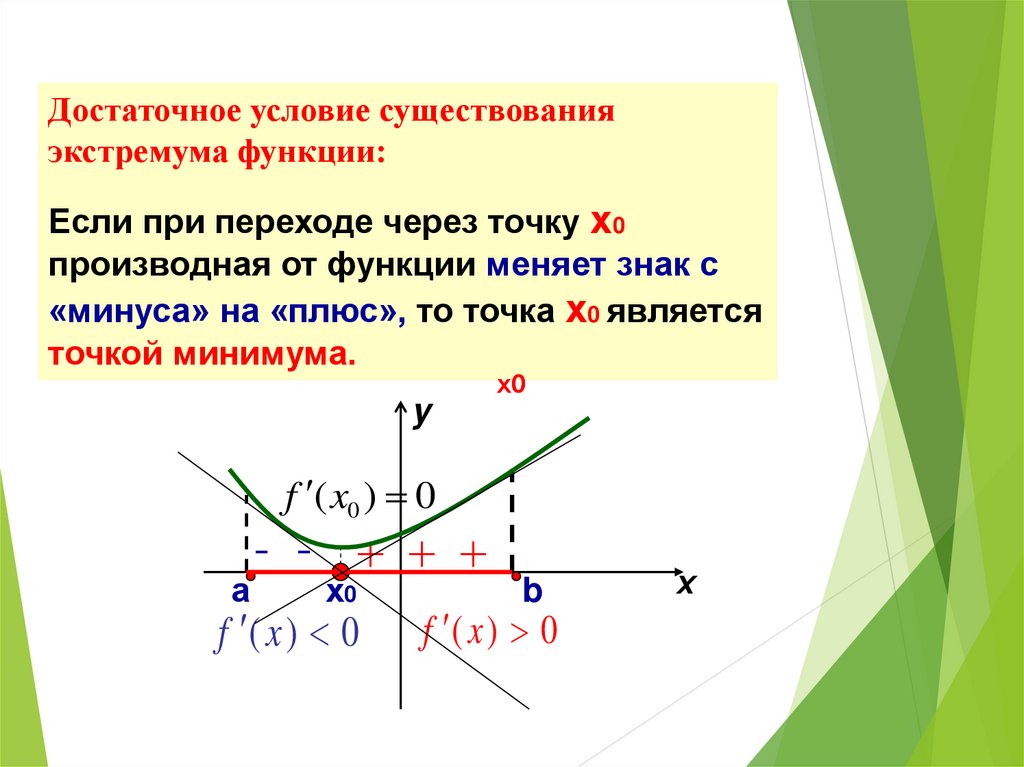
Достаточное условие существованияэкстремума функции:
Если при переходе через точку х0
производная от функции меняет знак с
«минуса» на «плюс», то точка х0 является
точкой минимума.
y
х0
f ( x0 ) 0
а
_ _
х0
f ( x ) 0
b
f ( x ) 0
х
23.
Алгоритм нахождения точек экстремумафункции:
1) найти производную функции;
2) найти критические точки, т.е.
решить уравнение f´(х)=0;
3) с помощью метода интервалов
определить знаки производной
в
х0
окрестностях критических точек;
4) используя достаточные условия
существования экстремума, найти
точки максимума и минимума
24.
Упрощенное нахождение точек максимума иминимума:
х=-2 – точка максимума,
х=0 – точка минимума
25.
Пример:Найдите точки экстремума функции
f(х)=2х4 – 4х2 +1
f´(х)= 8х3 – 8х
f´(х)=0 т.е. 8х3 – 8х =0
8х(х2 – 1)=0
8х=0
или
х2 – 1=0
х₁ =0
х2 =1
х₂ = -1; х3=1
Ответ: Хmax= 0;
Xmin =-1 , Xmin =1.
26. Решение упражнений.
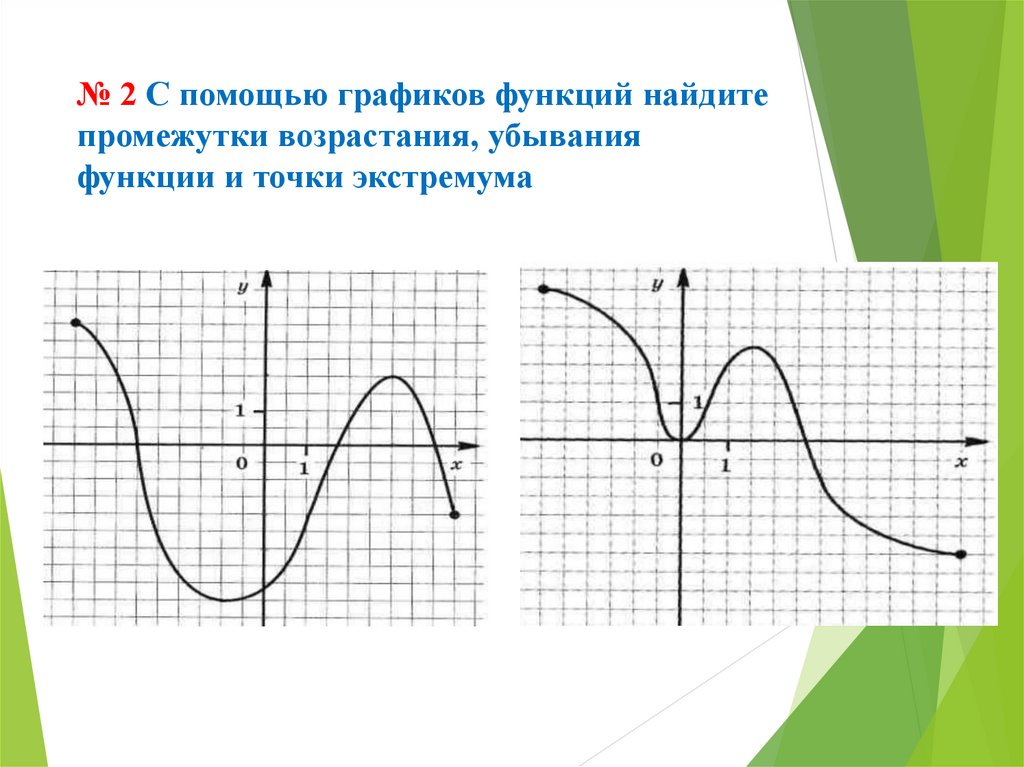
УСТНО:27. №1 В каких точках производная функции равна нулю? Не существует?
yу = f(х)
1
O 1
х1
х2
х3
х4
х5
х6
х7
x























 mathematics
mathematics








