Similar presentations:
Введение в теорию графов
1. ВВЕДЕНИЕ В ТЕОРИЮ ГРАФОВ
Желобаев А.Л. МИЭТ 2009.2. 1. Основные понятия теории графов
3. Ориентированный Граф G(V,E)
МНОЖЕСТВОДУГ
ВЕРШИНА D
МНОЖЕСТВО
ВЕРШИН
D
A
C
B
ДУГА {A,B}
ДУГА {B,A}
ЦИКЛ
(Петля)
4. Неориентированный Граф G(V,E)
ВЕРШИНА АD
МНОЖЕСТВО
ВЕРШИН
A
C
РЕБРО (A,B)
(B,A)=(A,B)
МНОЖЕСТВО
РЕБЕР
B
ВИСЯЧАЯ
ВЕРШИНА
E
ИЗОЛИРОВАННАЯ
ВЕРШИНА
5. Ориентированные и неориентированные графы
Ориентированныйграф G(V,E),
Неориентированный Подграф графа (а),
граф G(V,E),
порожденный
множеством
V = {1,2,3,4,5,6}
вершин {1,2,3,6}
V = {1,2,3,4,5,6}
E = {{1,2}, {2,2}, E = {(1,2), (1,5),
{2,4}, {2,5}, {4,1}, (2,5), (3,6)}
{4,5}, {5,4}, {6,3}}
6. Основные понятия
Вершина графаСмежная
Изолированная
Висячая
Степень вершины
исходящая,
входящая
Ребро (дуга) графа
Инцидентность
вес
Дуга-цикл
Совокупность дуг
Путь длины k
Цикл
Ациклический граф
Связный граф
Сильно связный граф
Полный граф
Пустой граф
Лес
Дерево в графе
7. Пути и циклы в графе
ID
G
A
J
C
H
B
E
F
8. Изоморфизм графов
ИЗОМОРФНЫЕ ГРАФЫНЕИЗОМОРФНЫЕ ГРАФЫ
9. Подграфы
G(V,E)Подграфы
G’(V’,E’)
D
D
A
A
C
C
B
B
E
E
G’ подграф G, если E’ E и V’ V
G’ суграф G, если E’ E и V’ = V
10. Клики в графе
DE
F
A
C
B
G
11. Двудольные графы
EA
D
B
F
C
G
12. Планарные и плоские графы
EA
D
B
A
E
F
C
Планарный
граф
D
B
F
C
Плоский
граф
13. 2. Алгоритмы на графах
14. Минимальные покрывающие деревья
Имеется граф G(V,E)Каждому ребру (u,v) задан неотрицательный
вес w(u,v)
Задача: найти подмножество Т Е,
связывающее все вершины, для которого
минимален суммарный вес
w(T)= w(u,v)
(u,v)εT
15. Отличия теории и практики
AB
А
D
A
C
B
B
D
A
C
B
C
кратчайшее дерево:
А - без дополнительных вершин
В - с дополнительной вершиной
С – дерево Штейнера
D
C
16. Алгоритм Краскала шаг 0
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 0
17. Алгоритм Краскала шаг 1
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 1
18. Алгоритм Краскала шаг 2
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 3
19. Алгоритм Краскала шаг 3
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 5
20. Алгоритм Краскала шаг 4
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 9
21. Алгоритм Краскала шаг 5
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 13
22. Алгоритм Краскала шаг 6
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 20
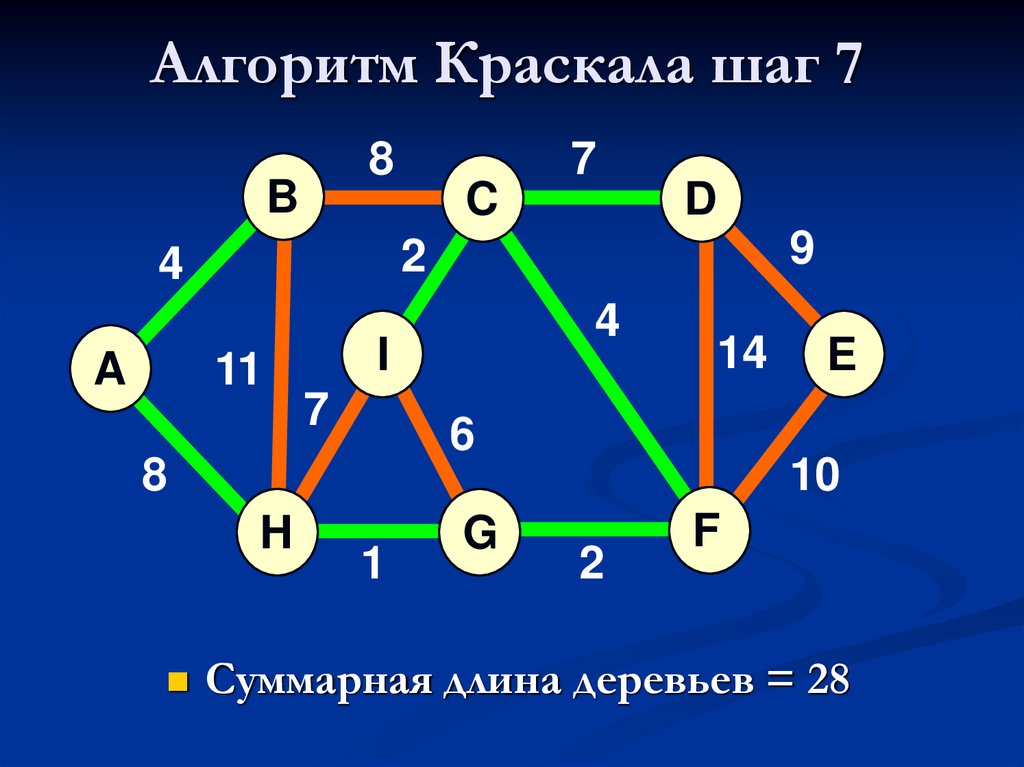
23. Алгоритм Краскала шаг 7
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 28
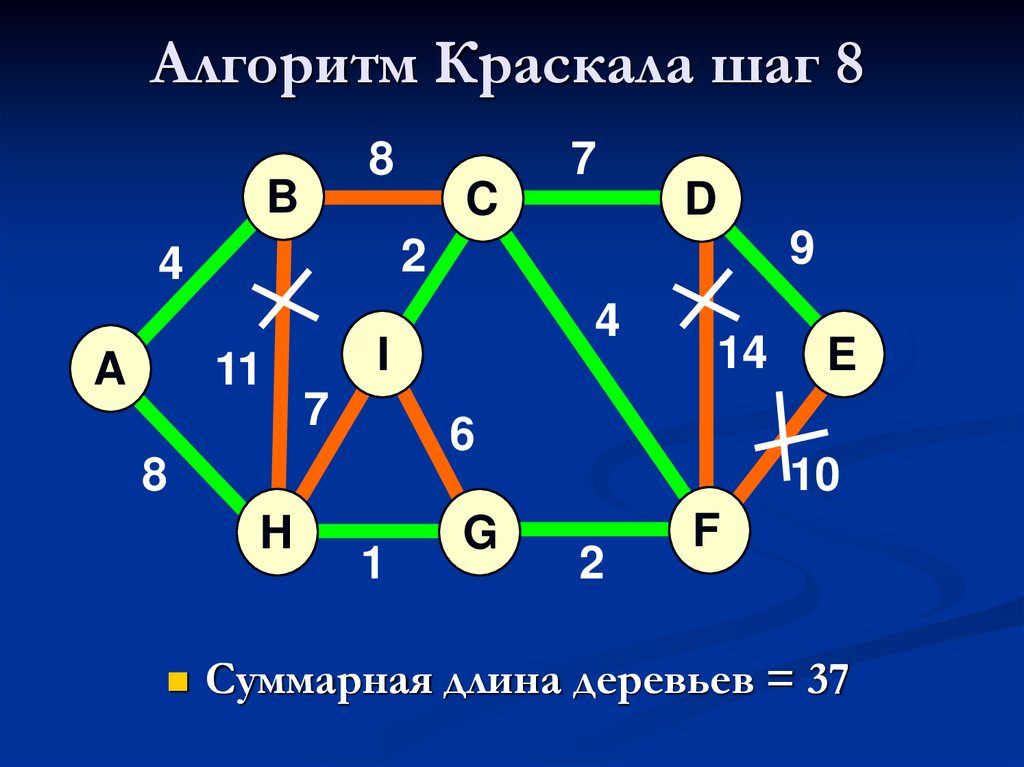
24. Алгоритм Краскала шаг 8
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина деревьев = 37
25. Алгоритм Краскала шаг 9
BC
7
D
9
2
4
4
I
A
E
8
H
1
G
2
F
Суммарная длина деревьев = 37
26. Алгоритм Прима
Начало алгоритма: с произвольнойвершины
К текущему дереву присоединяется
смежная вершина с кратчайшим ребром.
Окончание алгоритма: либо все вершины
подключены, либо невозможно
подключить ни одно ребро.
27. Алгоритм Прима шаг 0
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 0
28. Алгоритм Прима шаг 1
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 0
29. Алгоритм Прима шаг 2
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 4
30. Алгоритм Прима шаг 3
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 12
31. Алгоритм Прима шаг 4
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 14
32. Алгоритм Прима шаг 5
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 18
33. Алгоритм Прима шаг 6
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 20
34. Алгоритм Прима шаг 7
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 21
35. Алгоритм Прима шаг 8
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 28
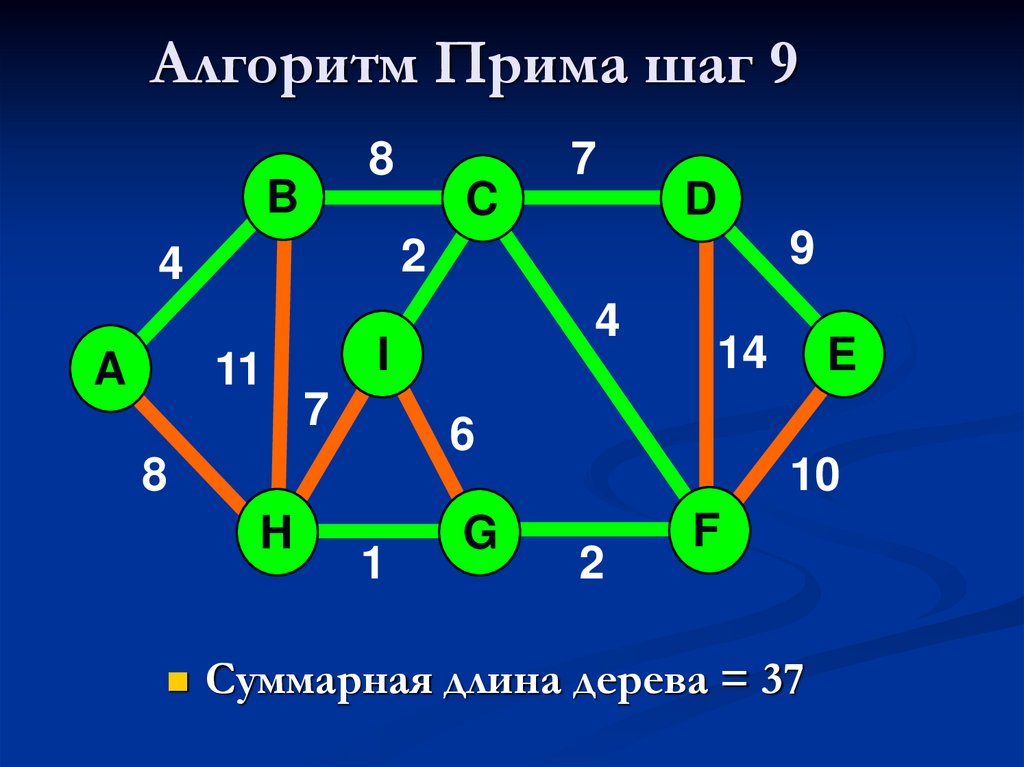
36. Алгоритм Прима шаг 9
8B
11
9
H
4
I
7
14
6
8
D
2
4
A
C
7
1
G
E
10
2
F
Суммарная длина дерева = 37
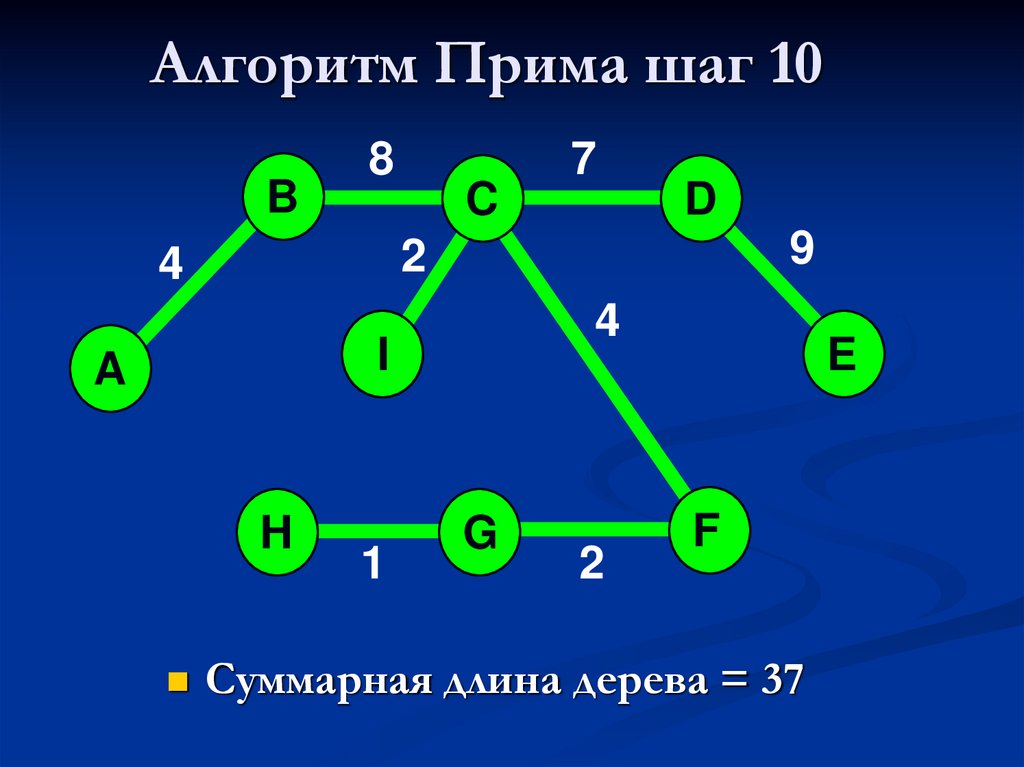
37. Алгоритм Прима шаг 10
B8
C
D
9
2
4
4
I
A
H
7
1
G
2
E
F
Суммарная длина дерева = 37
38. КРАТЧАЙШИЕ ПУТИ В ГРАФЕ
Алгоритм Дейкстры (Дийкстры)Алгоритм Ли
Алгоритм А* (А-звездочка)
39. Алгоритм Дейкстры
VU
1
8
10
3
S
2
0
9
4
6
7
5
X
2
Y
Ищем путь из S V
40. Алгоритм Дейкстры
VU
8
10
S
3
2
0
1
9
4
6
7
5
X
2
Y
41. Алгоритм Дейкстры
VU
8
10
10
S
3
2
0
1
9
4
6
7
5
5
X
2
Y
42. Алгоритм Дейкстры
VU
8
10
10
S
3
2
0
1
9
4
6
7
5
5
X
2
Y
43. Алгоритм Дейкстры
VU
8
8
10
S
3
2
0
1
14
9
4
6
7
5
5
X
2
7
Y
44. Алгоритм Дейкстры
VU
8
8
10
S
3
2
0
1
14
9
4
6
7
5
5
X
2
7
Y
45. Алгоритм Дейкстры
VU
8
8
10
S
3
2
0
1
13
9
4
6
7
5
5
X
2
7
Y
46. Алгоритм Дейкстры
VU
8
8
10
S
3
2
0
1
13
9
4
6
7
5
5
X
2
7
Y
47. Алгоритм Дейкстры
VU
8
8
10
S
3
2
0
1
9
9
4
6
7
5
5
X
2
7
Y
48. Алгоритм А* (Алгоритм оптимального поиска)
V’V
h(v)
g(v)
9
F
S
11
F(v)=g(v)+h(v)
49. Оценка длины пути
Минимальнаяоценка
Точная
длина
Манхеттеновская
длина
V
F
S
50. Алгоритм А*
g(v) – стоимость пути от финиша довершины v.
h(v) – нижняя оценка стоимости
пути от вершины v до старта.
f(v)=g(v)+h(v) – нижняя оценка
стоимости пути от старта к финишу
через вершину v.
51. Алгоритм А*
1. Среди вершин, смежных с конечной найтивершину V, имеющую наименьшую оценку
f(v).
2. Если вершина V не смежна с начальной, то
среди вершин, достижимых из V найти
вершину V’ с наименьшим значением f(v).
3. Продолжать, пока не будет достигнута
начальная вершина.















































 mathematics
mathematics








