Similar presentations:
Повышение качества преподавания математики и подготовки обучающихся с учетом результатов ГИА (ОГЭ) в 2021 году
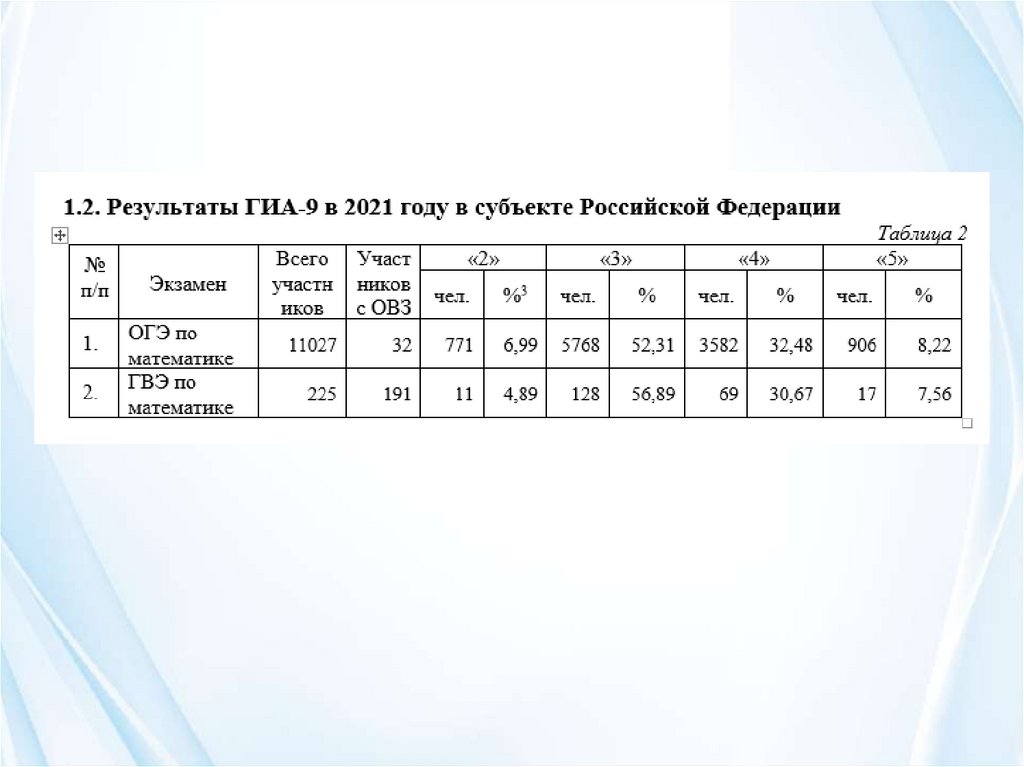
1. Повышение качества преподавания математики и подготовки обучающихся с учетом результатов ГИА (ОГЭ) в 2021 году
Автономное образовательное учреждение Вологодской областидополнительного профессионального образования
«Вологодский институт развития образования»
Повышение качества преподавания математики и подготовки
обучающихся с учетом результатов ГИА (ОГЭ) в 2021 году
Елена Михайловна Ганичева, методист сектора
предметных областей ОСП АОУ ВО ДПО
«Вологодский институт развития образования»
«Центр
непрерывного
повышения
профессионального мастерства педагогических
работников в г. Вологде»
Вологда, 2021 год
2.
3.
АОУ ВО ДПО «Вологодский институт развития образования»Шкала перевода первичных баллов ОГЭ
по математике в отметку по
пятибалльной шкале в 2021 году
Пятибалльная
шкала
Первичный
балл
«2»
«3»
«4»
«5»
15-21, не
22-31, не
7-14, не менее
менее 1
менее 1
1 балла
балла
балла
получено за
0 – 6 выполнение получено за получено за
выполнение выполнение
заданий по
*Соответствует шкале, рекомендованной ФГБНУ
«Федеральный
заданий по
заданий по
геометрии
институт педагогических измерений»
геометрии
геометрии
4.
АОУ ВО ДПО «Вологодский институт развития образования»Динамика успеваемости участников ОГЭ по математике в
Вологодской области (в основные сроки)
Год
Минимальный
балл
Количество
«2», %
Успеваемость, %
2011
7
650
91,8
2012
8
1457
85,5
2013
8
510
94,7
2014
4*
18
99,8
2015
4*
76
99,2
2016
4*
49
99,5
2017
4*
102
99,1
2018
8
723
93,5
2019
8
888
92,54
2021
7
771
93,01
5.
АОУ ВО ДПО «Вологодский институт развития образования»Динамика успеваемости участников ОГЭ по
математике в Вологодской области, %
99,8
94,7
91,8
85,5
99,2
99,5
99,1
93,5
92,54
93,01
6.
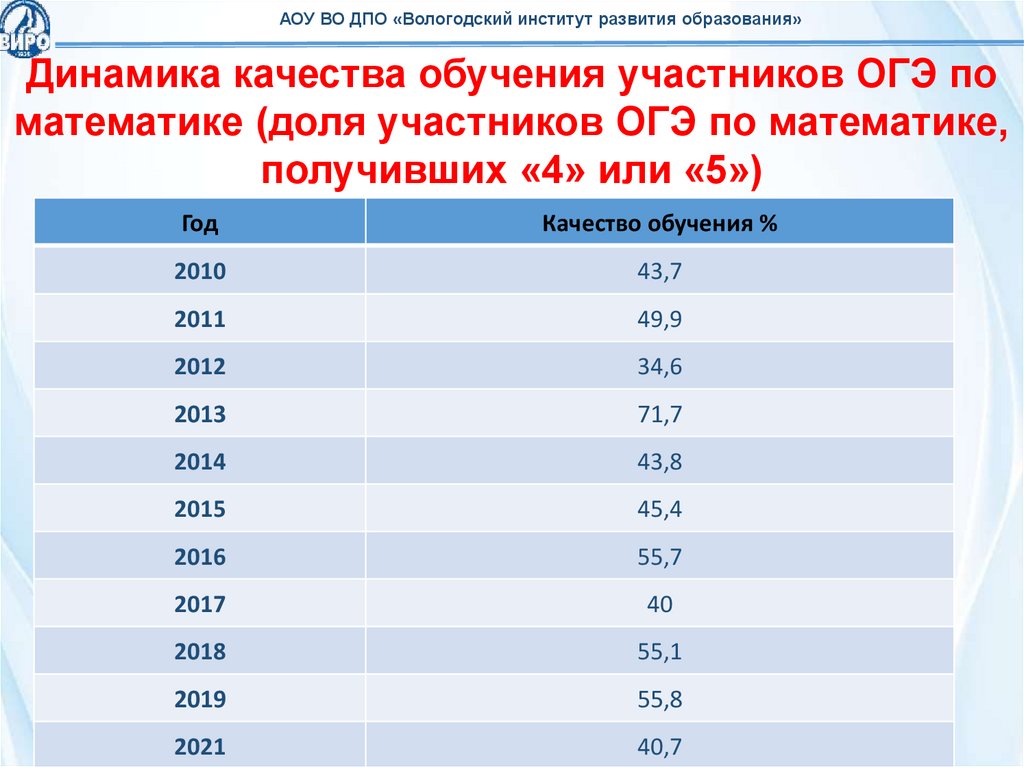
АОУ ВО ДПО «Вологодский институт развития образования»Динамика качества обучения участников ОГЭ по
математике (доля участников ОГЭ по математике,
получивших «4» или «5»)
Год
Качество обучения %
2010
43,7
2011
49,9
2012
34,6
2013
71,7
2014
43,8
2015
45,4
2016
55,7
2017
40
2018
55,1
2019
55,8
2021
40,7
7.
АОУ ВО ДПО «Вологодский институт развития образования»Динамика качества обучения (доли участников
ОГЭ по математике, получивших «4» или «5»), %
80
71,7
70
60
50
40
55,7
55,1
55,8
49,9
43,8
43,7
45,4
40
40,7
34,6
30
20
10
0
2010 г. 2011 г. 2012 г. 2013 г. 2014 г. 2015 г. 2016 г. 2017 г. 2018 г. 2019 г. 2021 г.
8.
Диаграмма распределения участников по первичным баллам900
825
800
775
763
699
741
723
693 701
700
668
580
600
568
515
500
432
391
400
307
300
204 206
167 182 181
200
68
100
141
108
92
34
64 79
26
48
8
22
30
31
0
0
32
33
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
9.
10.
11.
12.
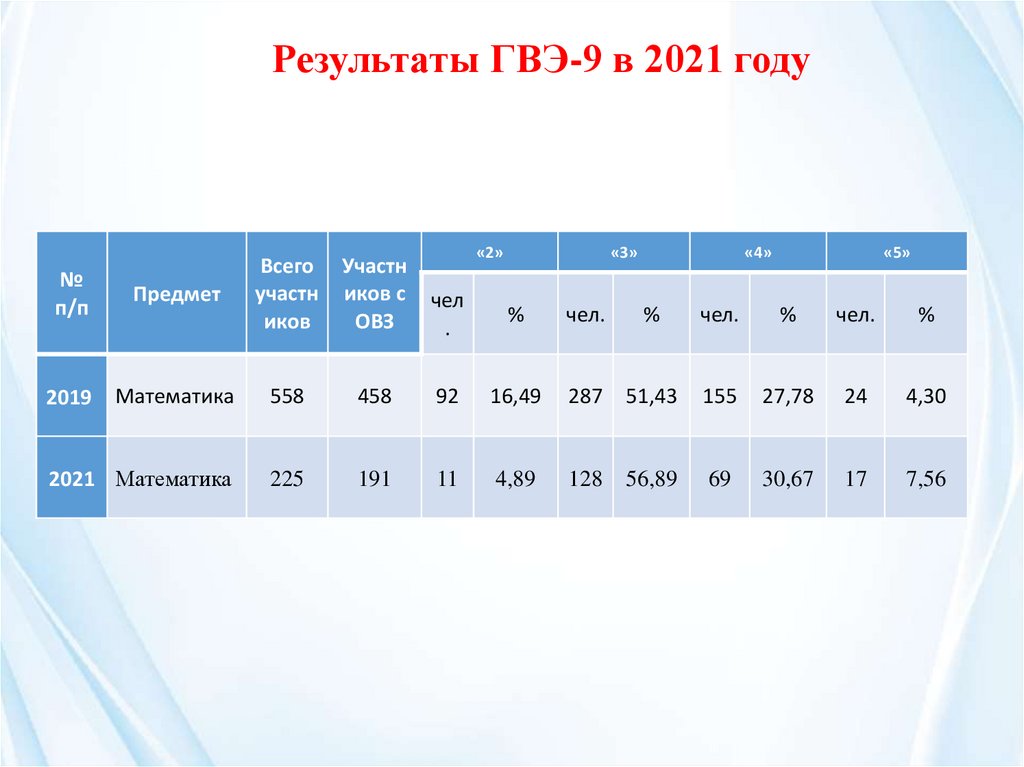
Результаты ГВЭ-9 в 2021 годуВсего Участн
участн иков с
иков
ОВЗ
№
п/п
Предмет
2019
Математика
558
2021 Математика
225
«2»
«3»
«4»
«5»
чел
.
%
чел.
%
чел.
%
чел.
%
458
92
16,49
287
51,43
155
27,78
24
4,30
191
11
4,89
128
56,89
69
30,67
17
7,56
13.
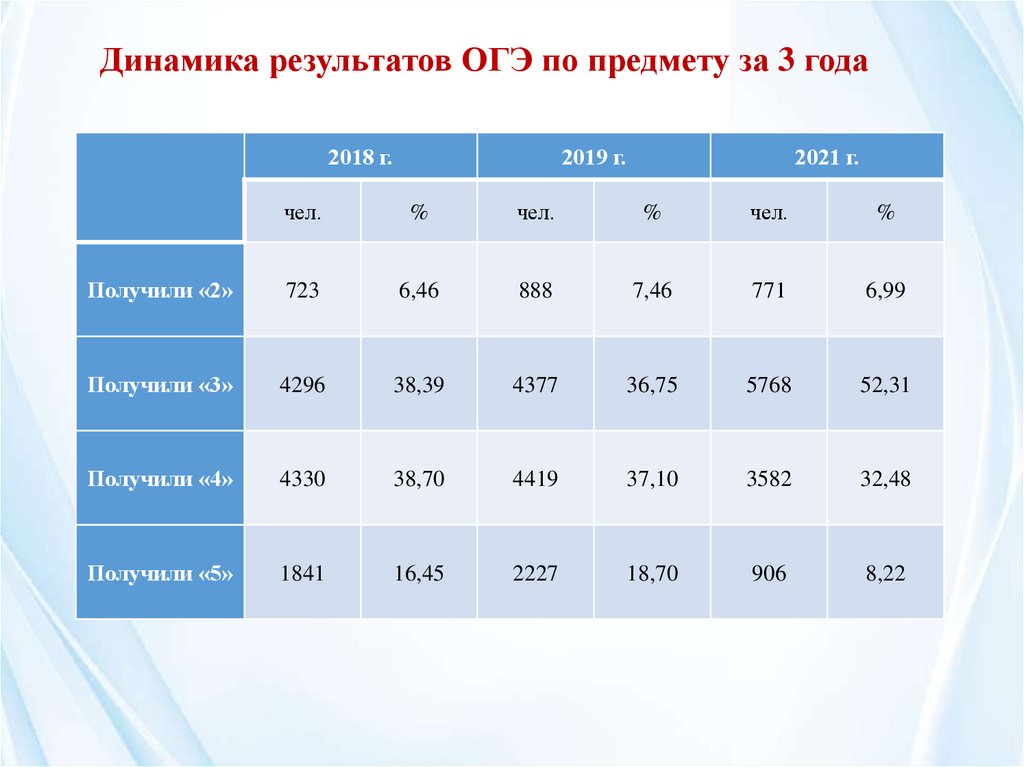
Динамика результатов ОГЭ по предмету за 3 года2018 г.
2019 г.
2021 г.
чел.
%
чел.
%
чел.
%
Получили «2»
723
6,46
888
7,46
771
6,99
Получили «3»
4296
38,39
4377
36,75
5768
52,31
Получили «4»
4330
38,70
4419
37,10
3582
32,48
Получили «5»
1841
16,45
2227
18,70
906
8,22
14.
Динамика результатов ОГЭ по математике7000
5768
6000
5000
4296 4377
4330
4419
4000
3582
3000
2227
1841
2000
1000
906
723 888 771
0
"2"
"3"
2018
"4"
2019
2021
"5"
15.
Год2017
68,67
2018
78,2
2019
74,49
2021
90,63
Задание 6 (в 2021 году)
16.
Год2017
82,18
2018
87,0
Задание 7 (в 2021 году)
17.
Год2019
87,02
2021
89,05
Задание 7 (в 2021 году)
18.
Год2017
65,29
2018
63,0
2019
55,59
2021
62,33
Задание 8 (в 2021 году)
19.
ГодЗадание 9 (в 2021 году)
2017
85,34
Решите уравнение: х2-36=0. Если уравнение имеет
более одного корня, в ответ запишите больший из
корней.
2018
75,2
Решите уравнение: х2+4х=21. Если уравнение
имеет более одного корня, в ответ запишите
меньший из корней.
2019
61,15
2021
59,33
Решите уравнение: 8х2=72х. Если уравнение имеет
более одного корня, в ответ запишите меньший из
корней.
20.
ГодЗадание 10 (в 2021 году)
2017 Вероятность того, что новая шариковая ручка пишет плохо
59,58 (или не пишет) равна 0,28. Покупатель в магазине выбирает
одну шариковую ручку. Найдите вероятность того, что эта
ручка пишет хорошо.
2018 На экзамене 50 билетов. Сеня не выучил 5 из них. Найдите
вероятность того, что ему попадется выученный билет.
78,2
2019 В лыжных гонках участвуют 13 спортсменов из России, 2
75,42 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок,
в котором спортсмены стартуют, определяется жребием.
Найдите вероятность того, что первым будет стартовать
спортсмен не из России.
2021 В фирме такси в данный момент свободно 20 машин: 2
81,49 чёрных, 5 жёлтых и 13 зелёных. По вызову выехала одна из
машин, случайно оказавшихся ближе всего к заказчику.
Найдите вероятность того, что к нему приедет жёлтое такси.
21.
Год2018
64,3
Задание 11 (в 2021 году)
22.
Год2019
72,06
Задание 11 (в 2021 году)
23.
Год2021
69,92
Задание 11 (в 2021 году)
24.
Год2018
73,3
Задание 12 (в 2021 году)
Чтобы перевести значение температуры по шкале Цельсия
в шкалу Фаренгейта, пользуются формулой tF =1,8tC+32,
где tC- температура в градусах Цельсия, tF – температура в
градусах Фаренгейта. Скольким градусам по шкале
Фаренгейта соответствует 55 градусов по шкале Цельсия?
2019
51,9
2021
70,89
В фирме «Эх, прокачу!» стоимость поездки на такси
(в рублях) длительностью более 5 минут
рассчитывается по формуле: C=150 +11(t-5), где t –
длительность поездки (в минутах). Пользуясь этой
формулой, рассчитайте стоимость 8-минутной
поездки. Ответ дайте в рублях.
25.
Год2018
63,5
2019
46,42
Задание 13 (в 2021 году)
26.
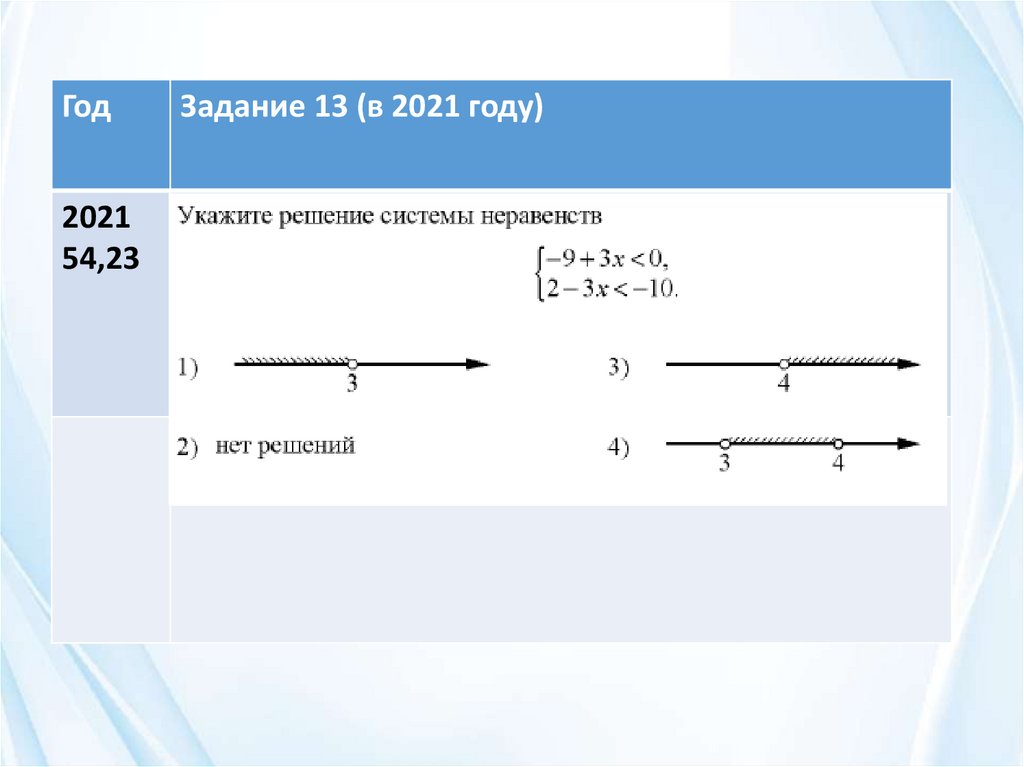
Год2021
54,23
Задание 13 (в 2021 году)
27.
ГодЗадание 14 (в 2021 году)
2018
51,8
Последовательность (сn) задана условиями с1=-4, сn-1= сn-2.
Найдите с8.
2019 Выписано несколько последовательных членов
87,04 арифметической прогрессии: ….; 10; х; 16; 19; …..
Найдите х.
2021 В амфитеатре 10 рядов. В первом ряду 25 мест, а в
75,22 каждом следующем на 3 места больше, чем в
предыдущем. Сколько мест в восьмом ряду
амфитеатра?
28.
ГодЗадание 15 (в 2021 году)
2017
19,77
Задание 9 (2016 г) (85,86%)
В треугольнике два угла равны 54° и 58°. Найдите его третий
угол. Ответ дайте в градусах.
Задание 9 (2017 г)
В треугольнике АВС угол А равен 30 , угол В равен 45 ,
ВС=8 2. Найдите АС.
2018
77,7
29.
Год2019
78,1
2021
47,32
Задание 1 (в 2021 году)
30.
Год2018
45,0
2019
35,66
2021
47,87
Задание 16 (в 2021 году)
31.
Год2018
52,5
2019
76,99
2021
76,94
Задание 17 (в 2021 году)
32.
Год2017
65,59
2018
79,8
Задание 18 (в 2021 году)
33.
Год2019
78,51
2021
72,65
Задание 18 (в 2021 году)
34.
Год2017
65,3
2018
55,3
Задание 19 (в 2021 году)
35.
ГодЗадание 19 (в 2021 году)
2019
73,74
Какое из следующих утверждений верно?
1) В параллелограмме есть два равных угла.
2) Каждая из биссектрис равнобедренного
треугольника является его медианой.
3) Площадь прямоугольного треугольника равна
произведению длин его катетов.
В ответ запишите номер выбранного утверждения.
2021
62,86
Какое из следующих утверждений верно?
1) Диагонали прямоугольной трапеции равны.
2) Существует прямоугольник, диагонали которого
взаимно перпендикулярны.
3) В тупоугольном треугольнике все углы тупые.
В ответ запишите номер выбранного утверждения.
36.
Задание 20 (2018, 19,3%)37.
Задание 20 (2019, 31,99%)Задание 20 (2021, 14,86%)
38.
39.
Задание 21 (2018. 23,0%)40.
Задание 21 (2019, 19,12%)Задание 21 (2021, 5,3%)
41.
42.
Задание 22 (2018, 6,9%)43.
Задание 22 (2019, 5,72%)Задание 22 (2021, 5,44%)
44.
45.
АОУ ВО ДПО «Вологодский институт развития образования»Задание 23 (2018 г., 9,6%)
Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD
равны соответственно 45° и 120°, а CD = 40.
Задание 23 (2019 г., 11,87%)
Катет и гипотенуза прямоугольного треугольника равны 21 и 75.
Найдите высоту, проведенную к гипотенузе.
Задание 23 (2021 г., 20,44%)
Высота АН ромба ABCD делит сторону CD на отрезки DH=24 и
CH=2. Найдите высоту ромба.
46.
47.
АОУ ВО ДПО «Вологодский институт развития образования»Задание 24 (2018 г., 6,9%)
Биссектрисы углов А и D параллелограмма ABCD пересекаются в
точке Е стороны ВС. Докажите, что Е – середина ВС.
Задание 24 (2019 г., 3,03%)
В остроугольном треугольнике АВС проведены высоты АА1 и СС1.
Докажите, что углы СС1А1 и САА1 равны.
Задание 24 (2021 г., 2,71%)
В остроугольном треугольнике АВС проведены высоты АА1 и ВВ1.
Докажите, что углы АА1В1 и АВВ1 равны.
48.
49.
АОУ ВО ДПО «Вологодский институт развития образования»Задание 25 (2018 г., 0,3%)
В треугольнике АВС известны длины сторон АВ=15, АС=25, точка О
– центр окружности, описанной около треугольника АВС. Прямая ВD,
перпендикулярная прямой ОА, пересекает сторону АС в точке D.
Найдите СD.
Задание 25 (2019 г., 0,33%)
В трапеции АВСD основания АD и ВС равны соответственно 48 и 24,
а сумма углов при основании АD равна 90°. Найдите радиус
окружности, проходящей через точки А и В и касающейся прямой СD,
если АВ=13.
Задание 25 (2021 г., 0,5%)
В трапеции АВСD боковая сторона АВ перпендикулярна основанию
ВС. Окружность проходит через точки С и D и касается прямой АВ в
точке Е. Найдите расстояние от точки Е до прямой СD, если
АD=14б ВС=12.
50.
51.
52.
53.
Средний процент выполнения заданий скратким ответом выпускниками 2021 года
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19
Все участники
Получившие "2"
Получившие "4"
Получившие "5"
Получившие "3"
54.
Средний процент выполнения заданий сразвернутым ответом выпускниками 2021 года
100
90
80
70
60
50
40
30
20
10
0
1
2
3
4
Все участники
Получившие "2"
Получившие "4"
Получившие "5"
5
Получившие "3"
6
55.
Результаты по содержательным разделам100,00
90,00
80,00
70,00
60,00
50,00
40,00
30,00
20,00
10,00
0,00
среднее_18
среднее_19
среднее_21
56.
Результаты по содержательным разделам60
50
40
30
20
10
0
"2"_2019
"2"_2021
часть 1
Числа и вычисления (1,2,3,4,5,6,8)
Алгебраические выражения (12)
Уравнения и неравенства (9,13)
Числовые последовательности (14)
Функции и графики (11)
Координаты на прямой и плоскости (7)
Геометрия (15,16,17,18,19)
Статистика и теория вероятностей (10)
57.
Результаты по содержательным разделам100,00
90,00
80,00
70,00
60,00
50,00
40,00
30,00
20,00
10,00
0,00
"3"_2019
"3"_2021
часть 1
Числа и вычисления (1,2,3,4,5,6,8)
Алгебраические выражения (12)
Уравнения и неравенства (9,13)
Числовые последовательности (14)
Функции и графики (11)
Координаты на прямой и плоскости (7)
Геометрия (15,16,17,18,19)
Статистика и теория вероятностей (10)
58.
Результаты по содержательным разделам120
100
80
60
40
20
0
"4"_2019
"4"_2021
часть 1
Числа и вычисления (1,2,3,4,5,6,8)
Алгебраические выражения (12)
Уравнения и неравенства (9,13)
Числовые последовательности (14)
Функции и графики (11)
Координаты на прямой и плоскости (7)
Геометрия (15,16,17,18,19)
Статистика и теория вероятностей (10)
59.
Результаты по содержательным разделам102
100
98
96
94
92
90
88
86
84
82
"5"_2019
"5"_2021
часть 1
Числа и вычисления (1,2,3,4,5,6,8)
Алгебраические выражения (12)
Уравнения и неравенства (9,13)
Числовые последовательности (14)
Функции и графики (11)
Координаты на прямой и плоскости (7)
Геометрия (15,16,17,18,19)
Статистика и теория вероятностей (10)
60.
61.
62.
63.
64.
65.
ОГЭПроблемные зоны, типичные ошибки
Результаты выполнения заданий базового уровня сложности: 4, 15, 16 части 1 нельзя
считать достаточными, т.е. на базовом уровне недостаточно сформированы:
• умения использовать приобретенные знания и умения в практической деятельности и
повседневной жизни;
• умение строить и исследовать простейшие математические модели;
• умение выполнять действия с геометрическими фигурами, координатами и векторами.
Трудности у выпускников вызвали задания повышенного уровня 20, 21, 24 части 2
(результаты выполнения этих заданий нельзя считать достаточными, поскольку они не
соответствуют планируемому результату, средний процент выполнения менее 15 %),
т.е. на повышенном уровне недостаточно сформированы умения:
•уметь решать уравнения, неравенства и их системы;
•умение строить и читать графики функций;
•умение строить и исследовать простейшие математические модели;
•выполнять действия с геометрическими фигурами, координатами и векторами;
•проводить доказательные рассуждения при решении задач, оценивать логическую
правильность рассуждений, распознавать ошибочные заключения (25);
Результаты выполнения заданий высокого уровня сложности: 22, 25 части 2 нельзя
считать достаточными (не соответствуют планируемому результату, средний процент
выполнения менее 15%), т.е. на высоком уровне недостаточно сформированы умения:
•умения выполнять преобразования алгебраических выражений, решать уравнения,
неравенства и их системы, строить и читать графики функций, строить и исследовать
66.
Рекомендуем усилить компетентностную составляющую преподаванияматематики за счет увеличения числа сюжетных задач, рассматриваемых на
уроках алгебры и геометрии. Это будет способствовать формированию у
обучающихся умения применять математические знания и решать практикоориентированные задачи.
Источники сюжетных задач:
1.Практико-ориентированные задания КИМ ОГЭ по математике. В 2020 году
в экзамен ОГЭ по математике В КИМ включён новый блок практикоориентированных заданий 1-5. В связи с этим, рассмотрим варианты
методических приёмов работы с этими заданиями в ходе подготовки к
экзамену.
67.
ученику даются подсказки в виде наводящих вопросов, аналогичных мини- заданий ипр., которые помогают найти верное решение.
Переформулирование условия. При выполнении заданий с практическим
содержанием, полезно выявить основную математическую составляющую из текста
условия и зафиксировать её в виде тезисов, основных мыслей. Также полезно
сложную задачу разбить над подзадачи, выявляя связи между величинами.
открытый банк тестовых заданий и демоверсии КИМов ФИПИ (https://fipi.ru/
1.Подборка материалов по оценке математической грамотности обучающихся в рамках
исследования PISA http://skiv.instrao.ru/bank-zadaniy/matematicheskaya-gramotnost/
Материалы электронного банка заданий для оценки функциональной грамотности
https://fg.resh.edu.ru/
68.
Для преодоления устойчивых ошибок рекомендуем при повторении курсагеометрии систематически проверять знание обучающимися основных
формул, формулировок теорем, свойств геометрических объектов, которые
часто используются при решении задач. Особое внимание должно быть
сконцентрировано на достижении осознанности знаний учащихся, на
умении применить полученные знания в практической деятельности, на
умении анализировать, сопоставлять, делать вывод. Рекомендуем
составлять опорные конспекты по темам курса геометрии, активно
использовать составление блоков задач при изучении тем курса геометрии,
применять
интерактивную
среду
Геогебра
для
демонстрации
геометрических объектов.
69.
Пример блока взаимосвязанных задач по теме: "Свойства прямоугольныхтреугольников".
Цель составления блока: отработка навыков использования свойств прямоугольных
треугольников от простейших до нестандартных задач.
Формулировки задач:
1.Найдите углы равнобедренного прямоугольного треугольника.
2.Один из острых углов прямоугольного треугольника на 24 больше другого. Найдите
острые углы треугольника
3.Один из острых углов прямоугольного треугольник в 4 раза меньше другого. Найдите эти
углы.
4.В треугольнике АВС ∠С – прямой, а ∠ В = 30 . Сторона АВ равна 5 см. Найти длину
стороны АС.
5.Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из
катетов равна 26,4 см. Найдите гипотенузу треугольника.
6.В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина
высоты — 6,1 см, длина боковой стороны — 12,2 см. Определи углы этого треугольника.
7.В треугольнике АВС ∠В = 90 ,СС1 – биссектриса, СС1=16см, ВС1=8см. Найдите внешний
угол при вершине А.
8.В треугольнике АВС ∠АСВ - тупой. Продолжения высот АА1, ВВ1, СС1 пересекаются в
точке О. Докажите, что ∠ АВС=∠АОС, ∠ОАС=∠ОВС.
9.В треугольнике АВС ∠С=90 , CD – высота треугольника, ВС=2BD. Докажите, что
AD=3DB.
70.
В блоке соблюдается принцип «от простого к сложному», варьируются всевозможные ситуации связей между условиями и заключением. В первых трех
задачах применяется знание суммы острых углов прямоугольного треугольника на
уровне программных знаний. Решение задач с четвертой
по шестую
предусматривает применение всех свойств прямоугольных треугольников как в
стандартных ситуациях, так и при небольших отклонениях от них. Решение
остальных задач требует умения применять знания в усложненных ситуациях, при
решении которых требуется творческий подход. Здесь приходится анализировать
сложные нестандартные геометрические ситуации, самостоятельно открывать
новые факты, устанавливать отношения между ними.
71.
Подготовка школьников к решению геометрических задач(по материалам ОГЭ и ЕГЭ) / Департамент образования Вологодской
области, Вологодский институт развития образования ;
[составители: Васильева Т.В., Панфилова Т.Л., Шилова Г.Н.]. – Вологда:
ВИРО, 2019.
https://viro.edu.ru/attachments/article/10238/1744.pdf
Перейти порог возможно! : сборник тренировочных заданий для
подготовки к итоговой государственной аттестации выпускников
основной школы : (для учащихся с низкой математической подготовкой)
/ Департамент образования Вологод. обл., Вологод. ин-т развития
образования ; [сост.: Е.М. Ганичева]. – Вологда: ВИРО, 2016.
https://viro.edu.ru/attachments/article/7966/2016_4.pdf
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
однотарифному плану от87.
88.
89.
Основные методы решения уравненийКлючевые слова: решение уравнения, тождественное
преобразование, тождественные преобразования, посторонний
корень, потеря корня.
Решение уравнения – это процесс, состоящий в основном в замене
заданного уравнения другим уравнением, ему равносильным. Такая
замена называется тождественным преобразованием.
90.
Основные тождественные преобразования:Замена одного выражения другим, тождественно равным
ему. Например, уравнение ( 3x+ 2 ) 2 = 15x+10 можно заменить
следующим равносильным: 9x2 + 12x + 4 = 15x + 10
Перенос членов уравнения из одной стороны в другую с обратными знаками. Так, в
предыдущем уравнении мы можем перенести все его члены из правой части в левую
со знаком « – »: 9x2 + 12x + 4 – 15x – 10 = 0, после чего получим: 9x2 – 3x – 6 = 0 .
Умножение или деление обеих частей уравнения на одно и то же выражение
(число), отличное от нуля. Это очень важно, так как новое уравнение может не
быть равносильным предыдущему, если выражение, на которое мы умножаем или
делим, может быть равно нулю. Уравнение x – 1 = 0 имеет единственный
корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение ( x – 1 )( x – 3 ) = 0,
у которого два корня: x = 1 и x = 3. Последнее значение не является корнем заданного
уравнения x – 1 = 0. Это так называемый посторонний корень. И наоборот, деление
может привести к потере корня. Так, если ( x – 1 )( x – 3 ) = 0 является исходным
уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x –
3.
Можно возвести обе части уравнения в нечетную степень или извлечь из обеих
частей уравнения корень нечетной степени. Необходимо помнить, что: а)
возведение в четную степень может привести к приобретению посторонних
корней; б) неправильное извлечение корня четной степени может
привести к потере корней.
91.
92.
93.
94.
95.
96.
97.
https://padlet.com/ganichevaem/r84zsxsvrqj992n998.
Курсы повышения квалификации в 2021 году99.
Направления деятельности:Подготовка к ГИА
Готовимся к переходу на
обновленный ФГОС (вступает
в действие с 01.09.2022 года)
•анализ результатов района / города
/ школы
•ознакомиться с КИМ 2022
•определить суть изменений,
(кодификатор, спецификация,
ознакомиться с примерной
демоверсия, критерии оценивания), программой по математике (сайт
проинформировать учеников и их
Института стратегии развития
родителей
образования)
•провести диагностику, определить
группы для адресной подготовки
•для обучающихся «группы риска»
будем проводить тестирования по
минимальному набору заданий
В рабочие программы
внести изменения в
тематическое планирование
с учетом программы
воспитания
100.
https://instrao.ru/101.
Новая примерная программа по математике (проект)ГЕОМЕТРИЯ
АЛГЕБРА
ВЕРОЯТНОСТЬ И
СТАТИСТИКА
© ГК «Просвещение», 2021
Информация с сайта ФГБНУ «Институт стратегии развития образования РАО»
101
102.
103.
104.
105.
106.
107.
108.
109.
Личностный результатВоспитательный потенциал
учебного предмета химии
Патриотического воспитания
Первоначальные химические понятия
понимания значения химической науки Роль химии в жизни человека.
в жизни современного общества,
Химия в системе наук
ценностного отношения к
Понятие о методах познания в химии.
отечественному культурному,
Важнейшие представители
историческому и научному
неорганических веществ
наследию,
Ряд активности металлов (Н. Н. Бекетов)
способности владеть достоверной
Атомно-молекулярное учение
информацией о передовых
достижениях и открытиях мировой (М.В.Ломоносов)
и отечественной химии,
Периодический закон.
заинтересованности в научных
Периодический закон и периодическая
знаниях об устройстве мира и
система химических элементов Д. И.
общества;
Менделеева
Д. И. Менделеев — учёный и гражданин.
110.
Личностный результатВоспитательный потенциал
учебного предмета химии
Формирования культуры здоровья Важнейшие представители неорганических
осознания ценности жизни,
веществ
ответственного отношения к
наблюдение взаимодействия
своему здоровью,
веществ с кислородом и условия
установки на здоровый образ жизни,
возникновения и прекращения горения
осознания последствий и
(пожара)
неприятия вредных привычек
Неметаллы и их соединения
(употребления алкоголя,
действие хлора и хлороводорода на организм
наркотиков, курения),
необходимости соблюдения правил
человека, оксиды углерода, их физические и
безопасности при обращении с
химические свойства, действие на живые
химическими веществами в быту организмы, понятие о биологически важных
и реальной жизни;
веществах: жирах, белках, углеводах — и их
роли в жизни человека.
Химия и окружающая среда
Химия и здоровье.
Безопасное использование веществ и
химических реакций в быту.
Первая помощь при химических ожогах
и отравлениях.
111.
112.
113.
114.
115.
116.
117. Спасибо за внимание!
АОУ ВО ДПО «Вологодский институт развития образования»Спасибо за внимание!














































































































 education
education







