Начертательная геометрия

1.

Начертательная геометрия
1 семестр
для студентов ф-та ИУ
ЛЕКЦИИ 6,7
Пересечение прямой линии с поверхностью.
Пересечение поверхностей.
Теорема Монжа.
Подготовили:
доценты кафедры РК-1 Сенченкова Л.С., Палий Н.В.

2.

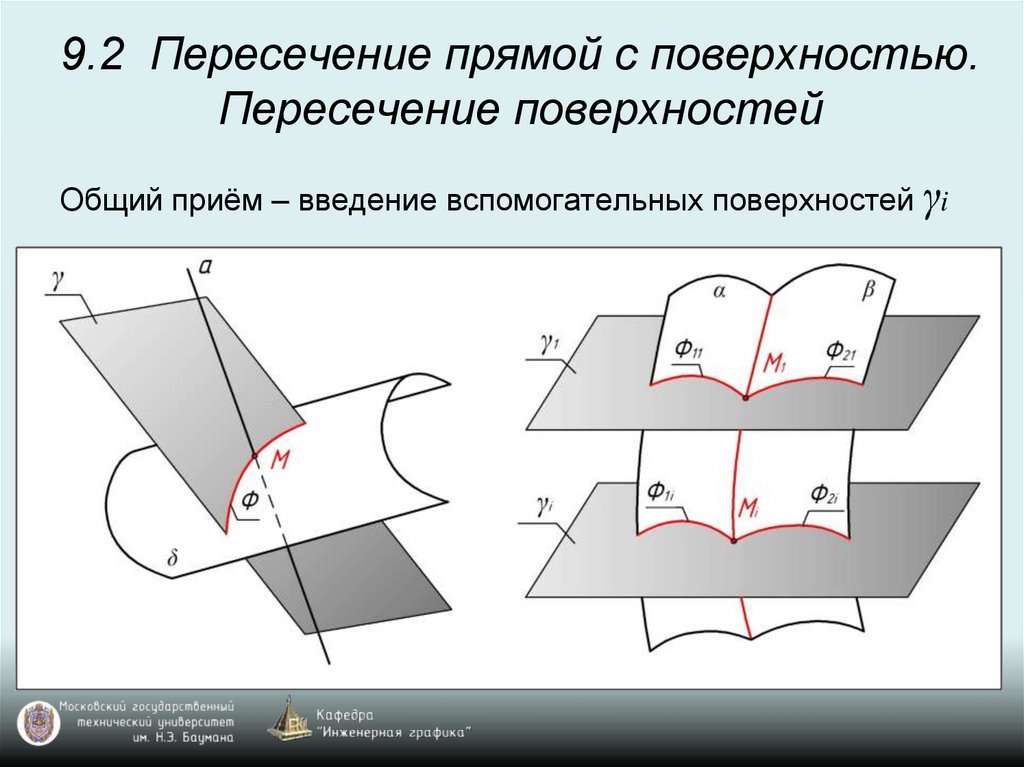
9.2 Пересечение прямой с поверхностью.
Пересечение поверхностей
Общий приём – введение вспомогательных поверхностей γi

3.

9.2 Пересечение прямой с поверхностью.
Пересечение поверхностей
Общий приём – введение вспомогательных поверхностей γi

4.

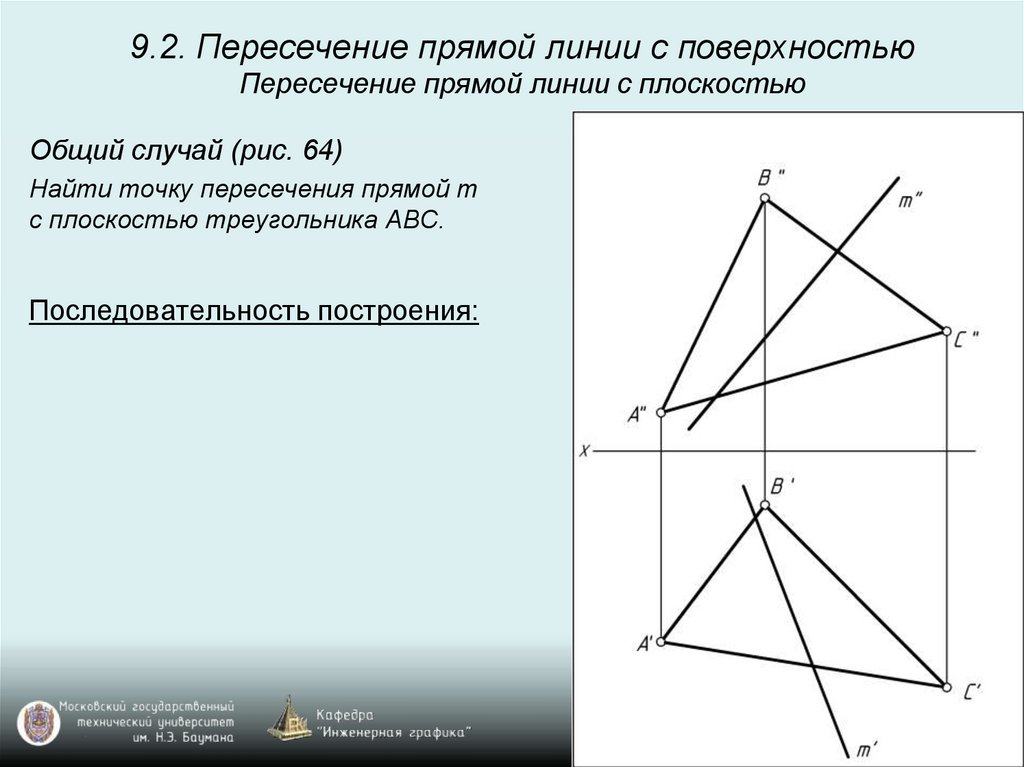
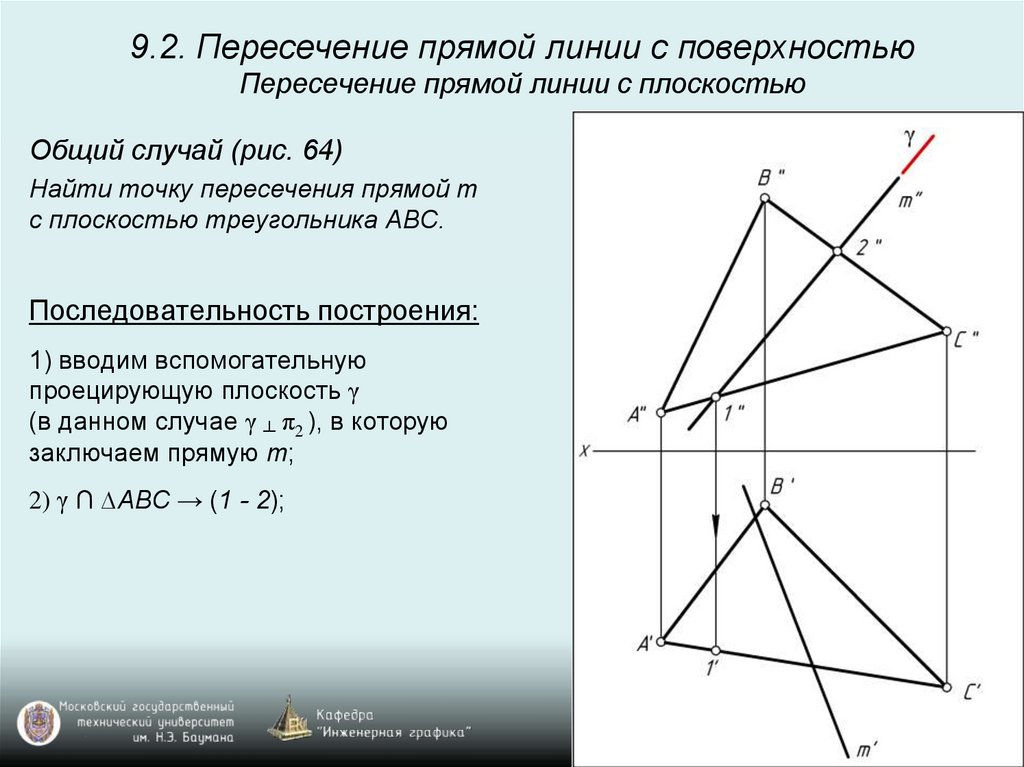
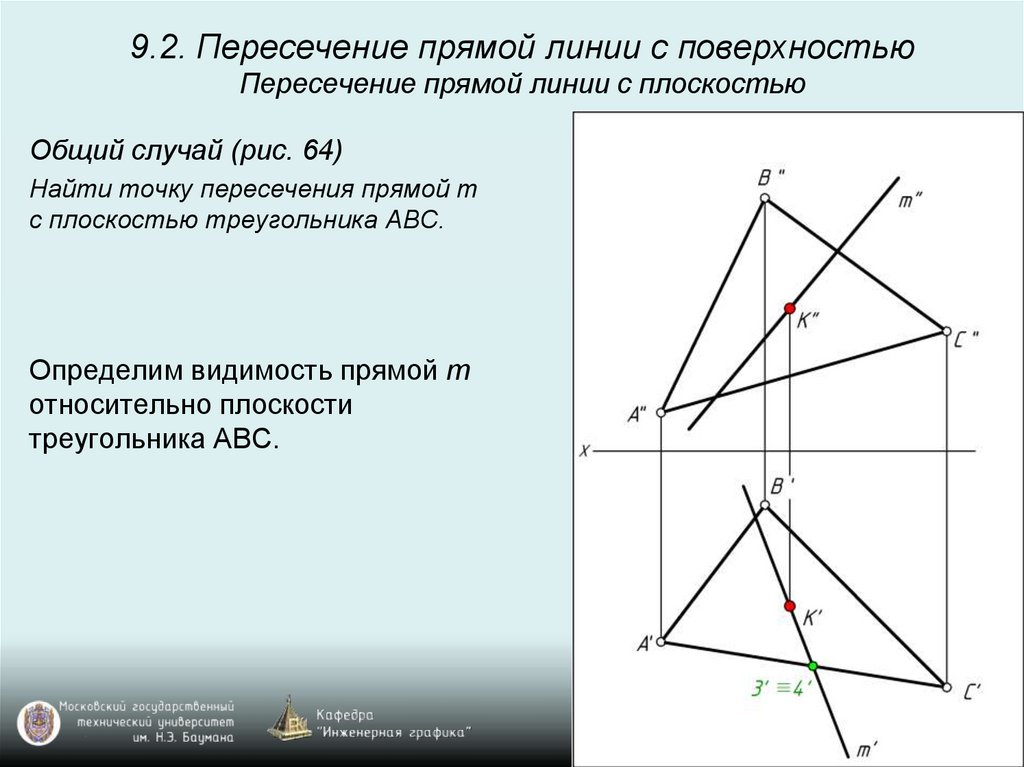
9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:

5.

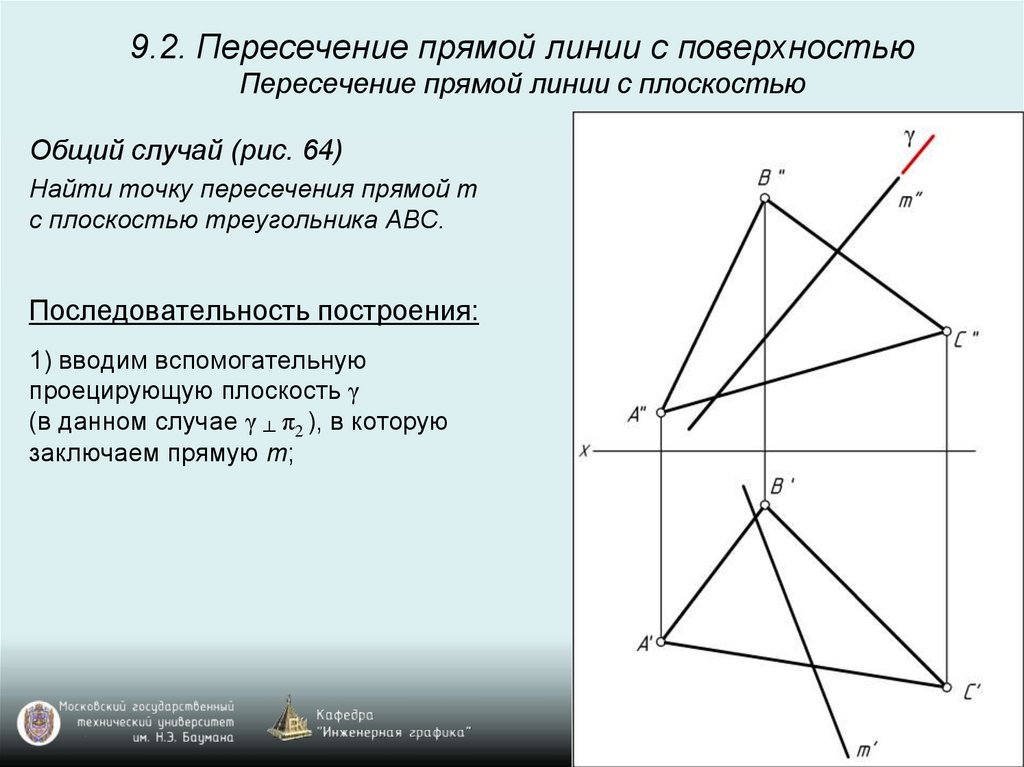
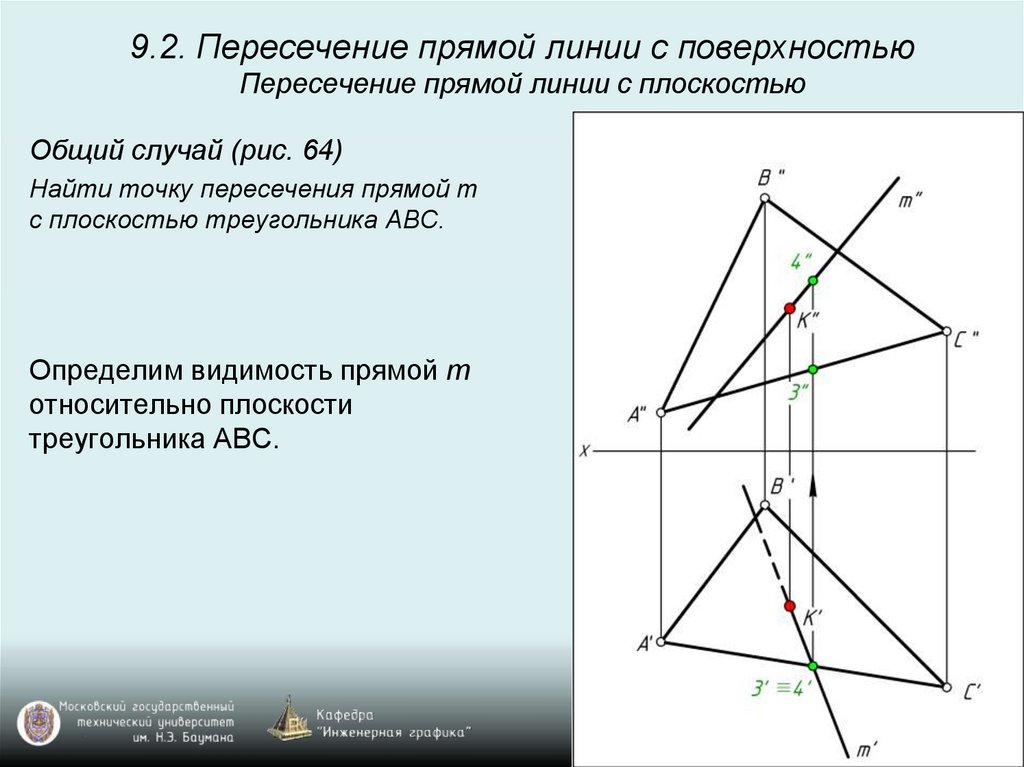
9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;

6.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
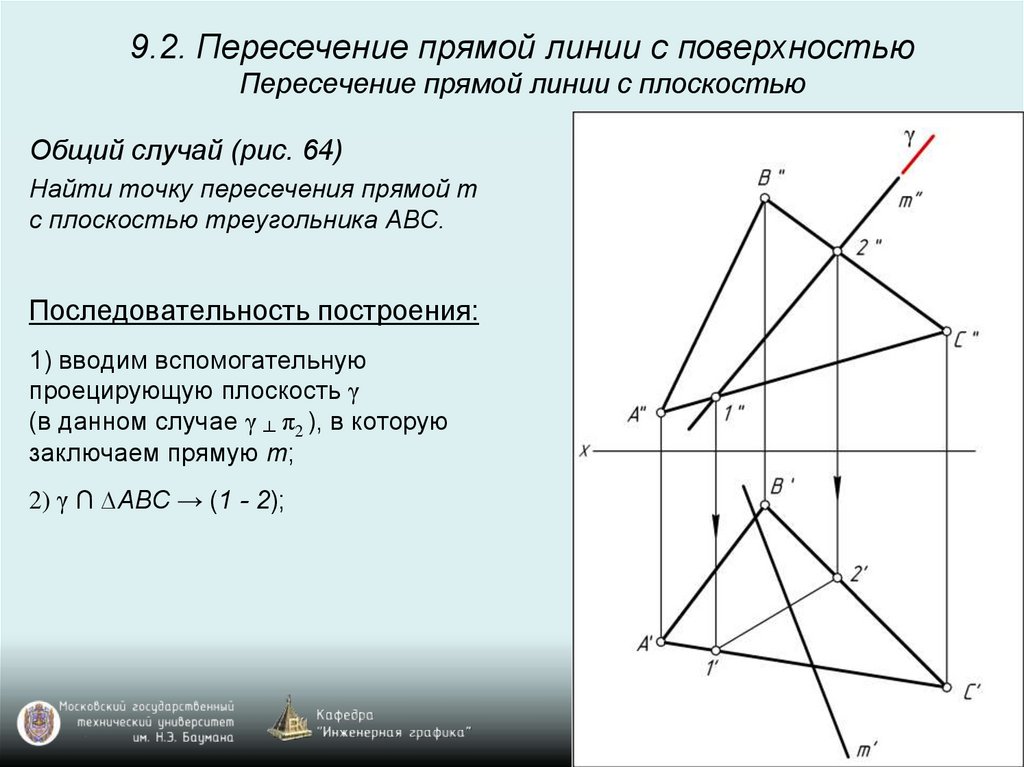
2) γ ∩ ∆ABC → (1 - 2);

7.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
2) γ ∩ ∆ABC → (1 - 2);

8.

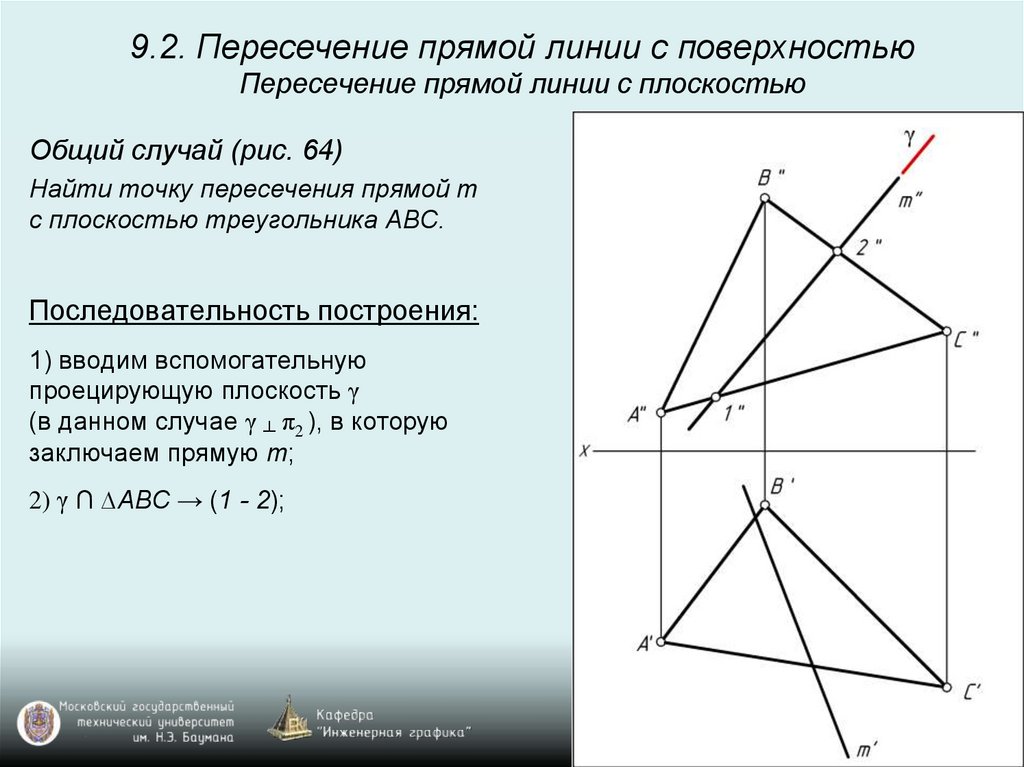
9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
2) γ ∩ ∆ABC → (1 - 2);

9.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
2) γ ∩ ∆ABC → (1 - 2);

10.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
2) γ ∩ ∆ABC → (1 - 2);
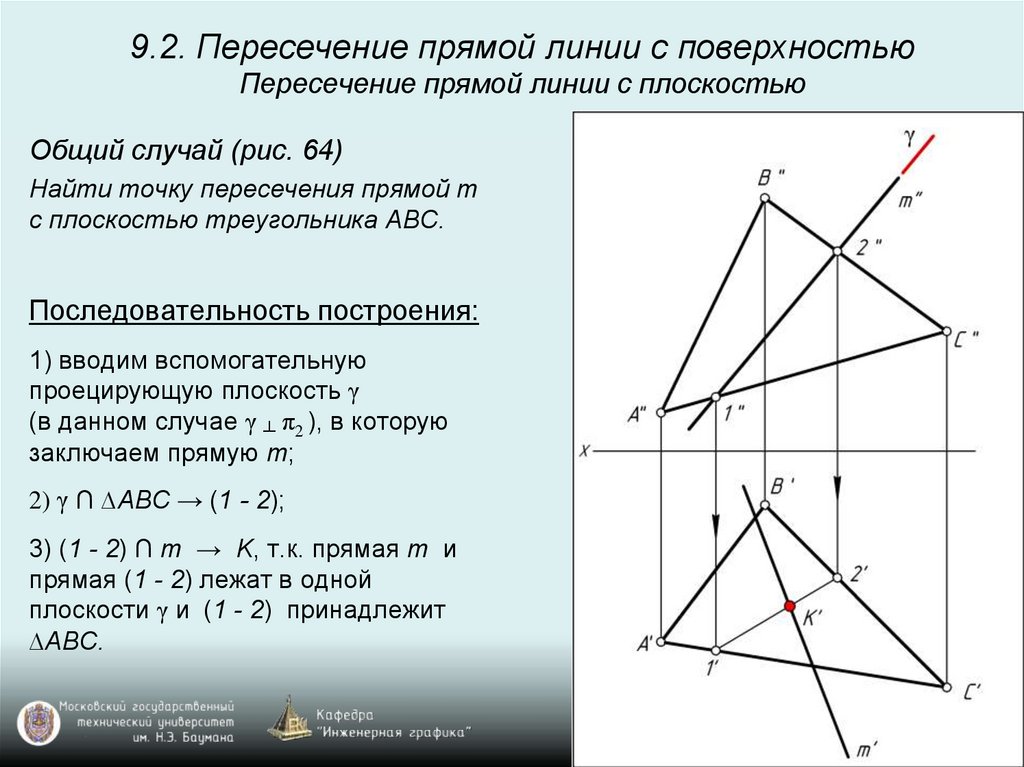
3) (1 - 2) ∩ m → K, т.к. прямая m и
прямая (1 - 2) лежат в одной
плоскости γ и (1 - 2) принадлежит
∆ABC.

11.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в которую
заключаем прямую m;
2) γ ∩ ∆ABC → (1 - 2);
3) (1 - 2) ∩ m → K, т.к. прямая m и
прямая (1 - 2) лежат в одной
плоскости γ и (1 - 2) принадлежит
∆ABC.

12.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
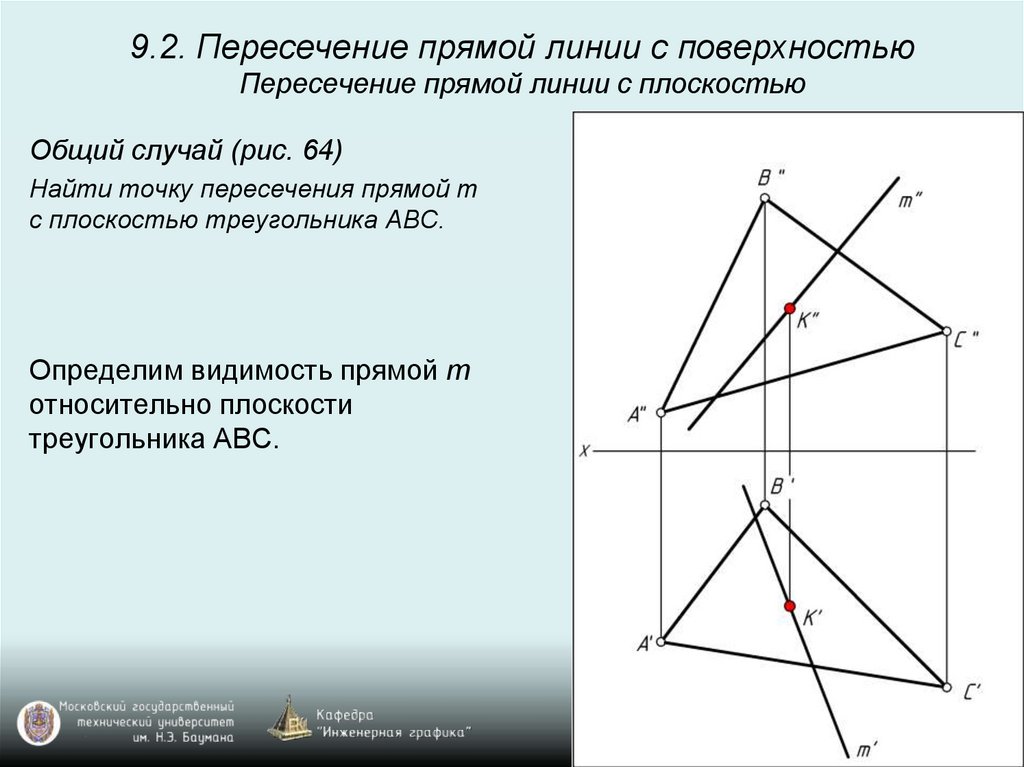
Определим видимость прямой m
относительно плоскости
треугольника АВС.

13.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

14.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

15.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

16.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

17.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

18.

9.2. Пересечение прямой линии с поверхностью
Пересечение прямой линии с плоскостью
Общий случай (рис. 64)
Найти точку пересечения прямой m
с плоскостью треугольника ABC.
Определим видимость прямой m
относительно плоскости
треугольника АВС.

19.

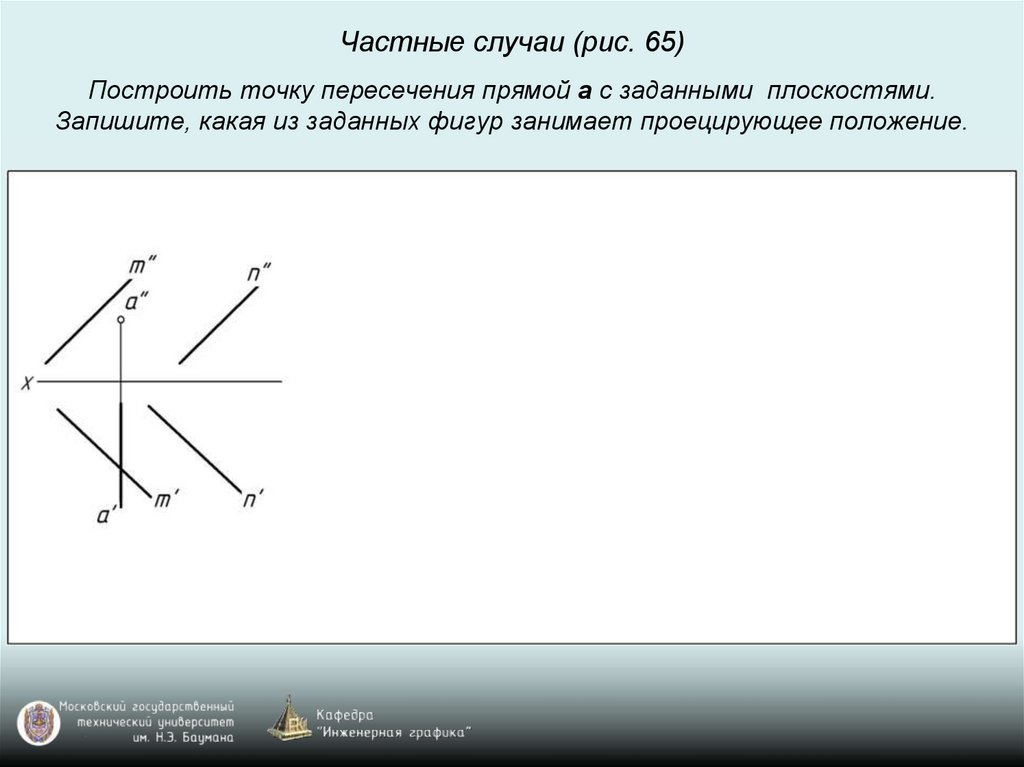
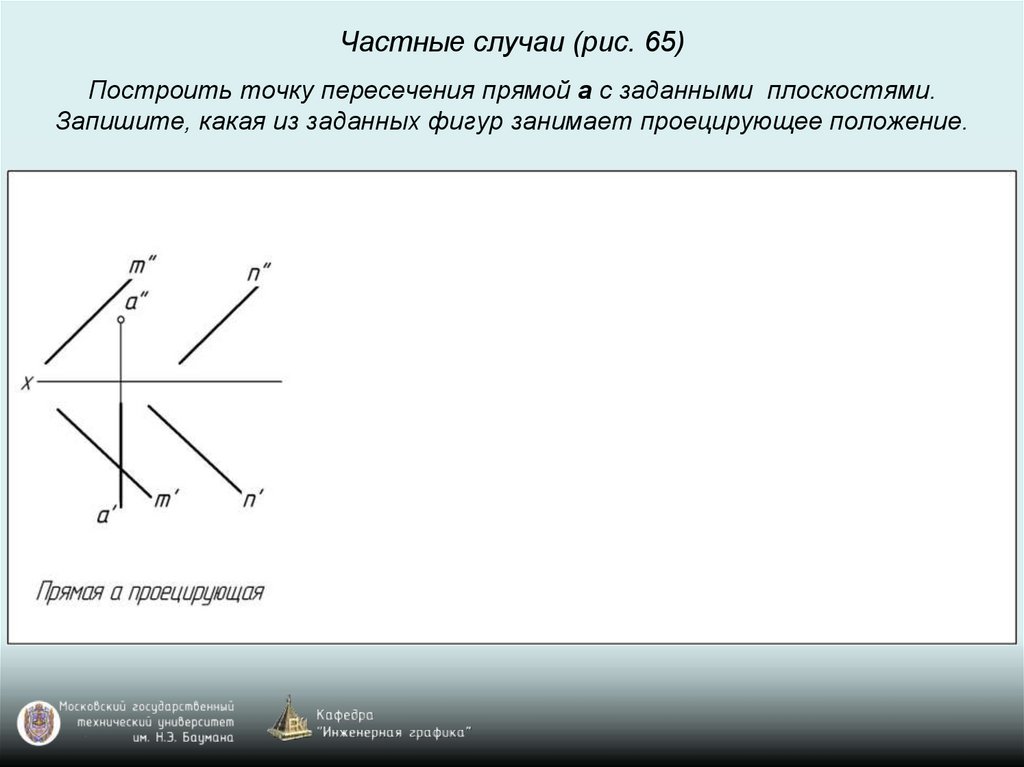
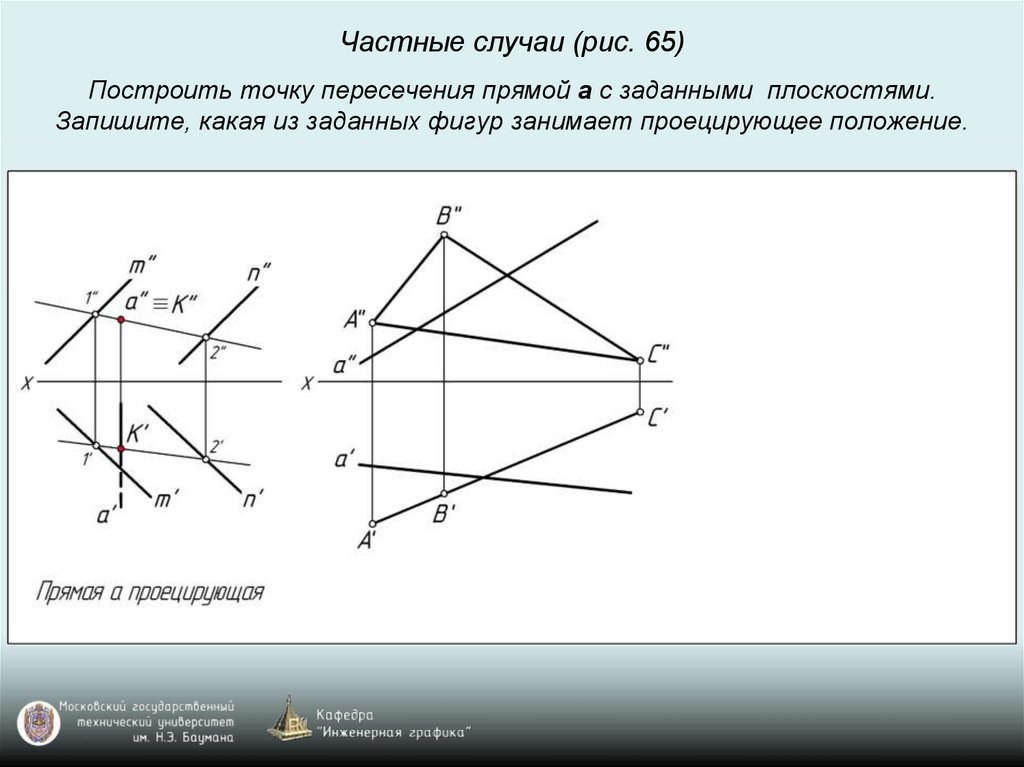
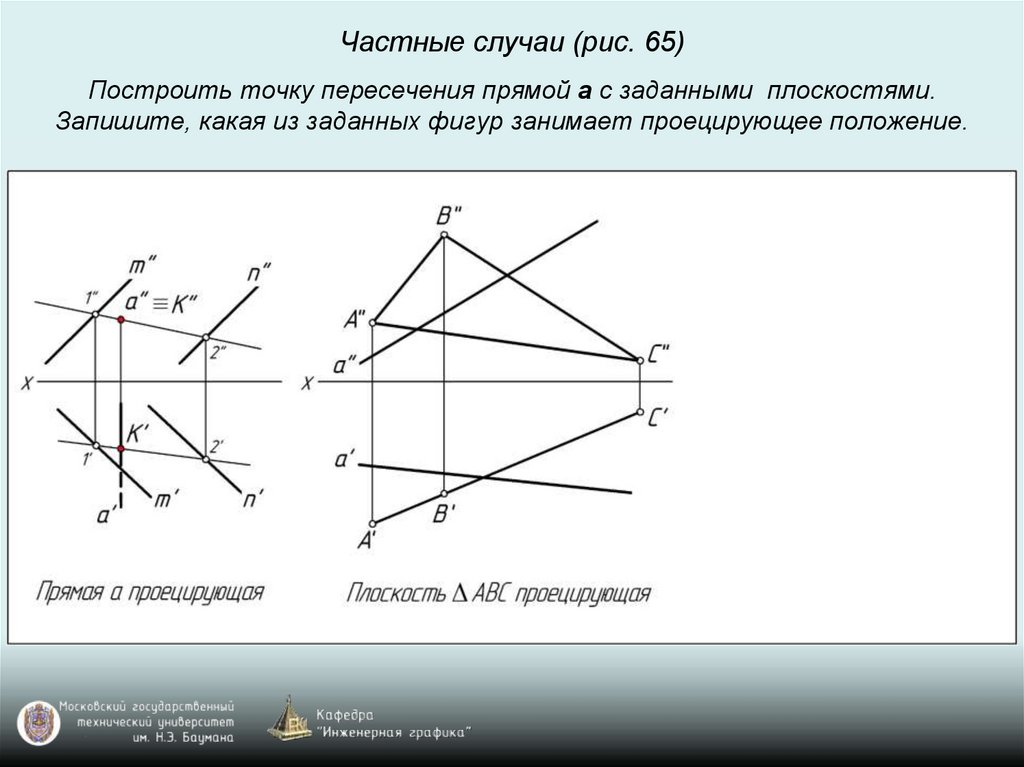
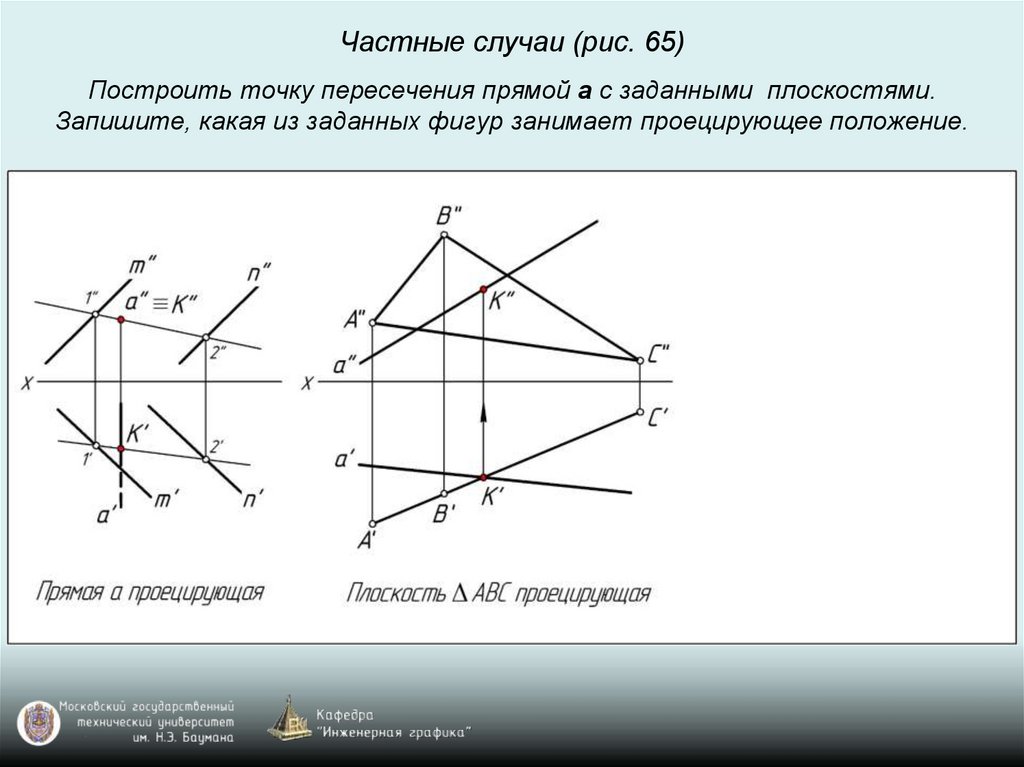
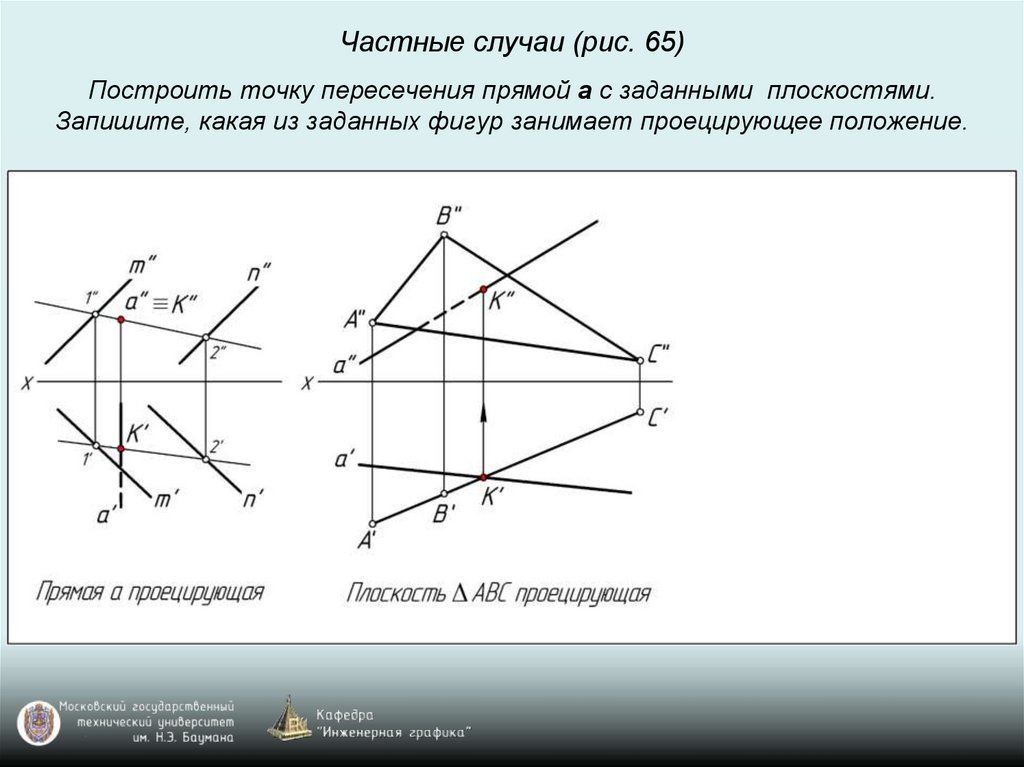
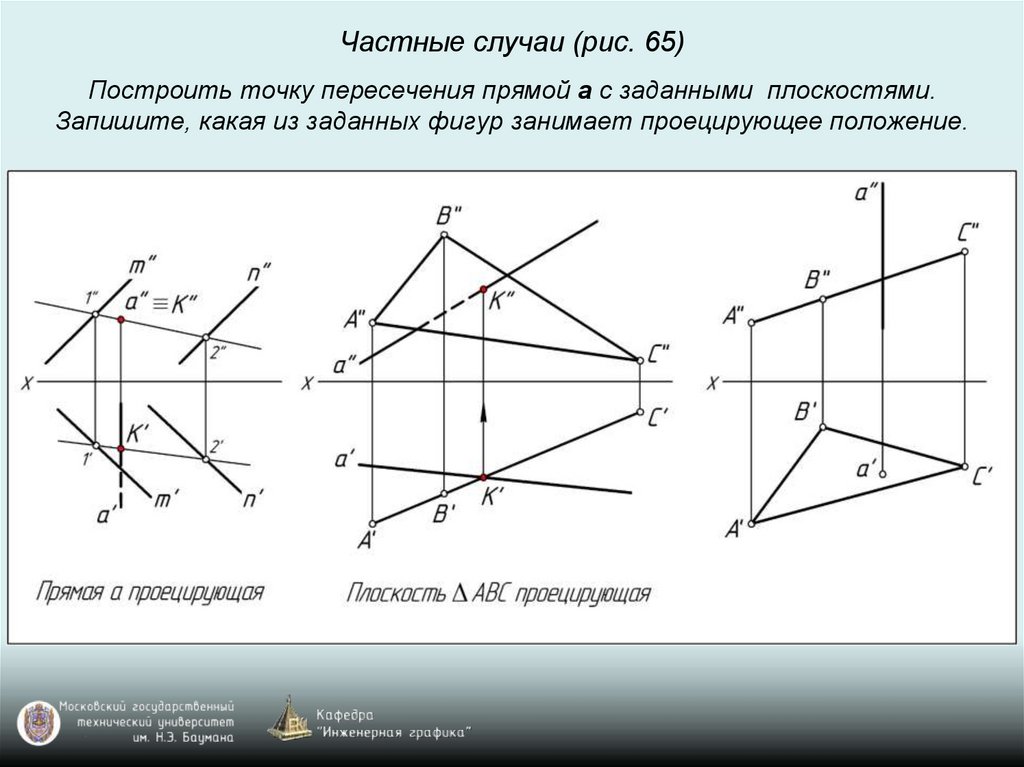
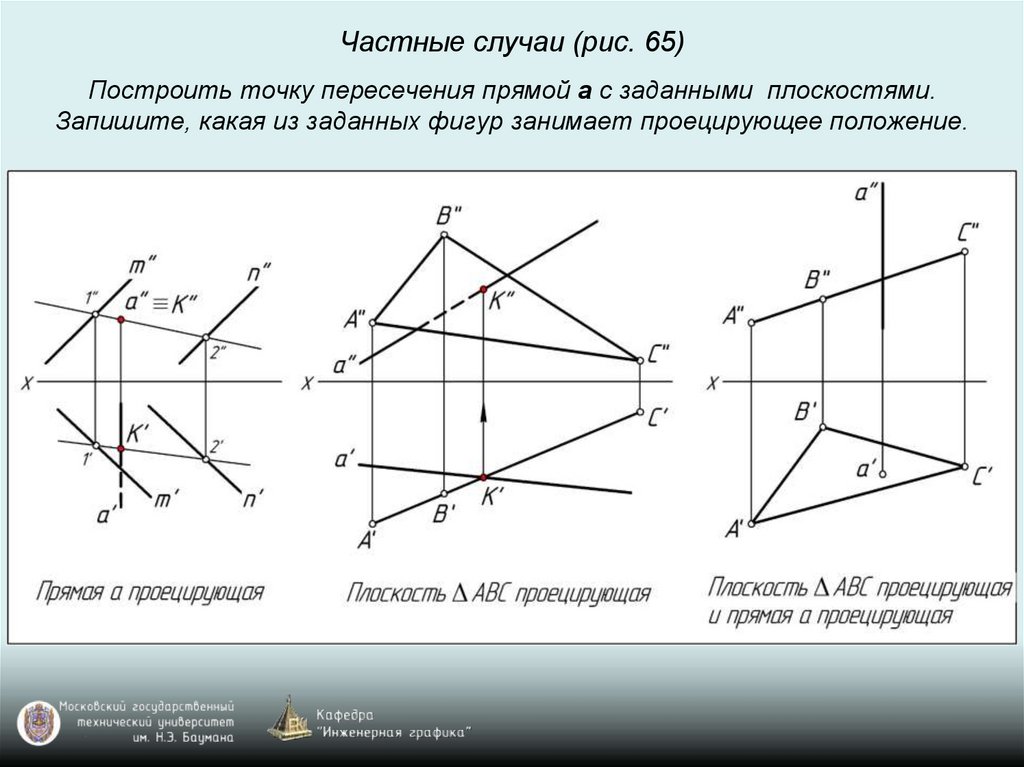
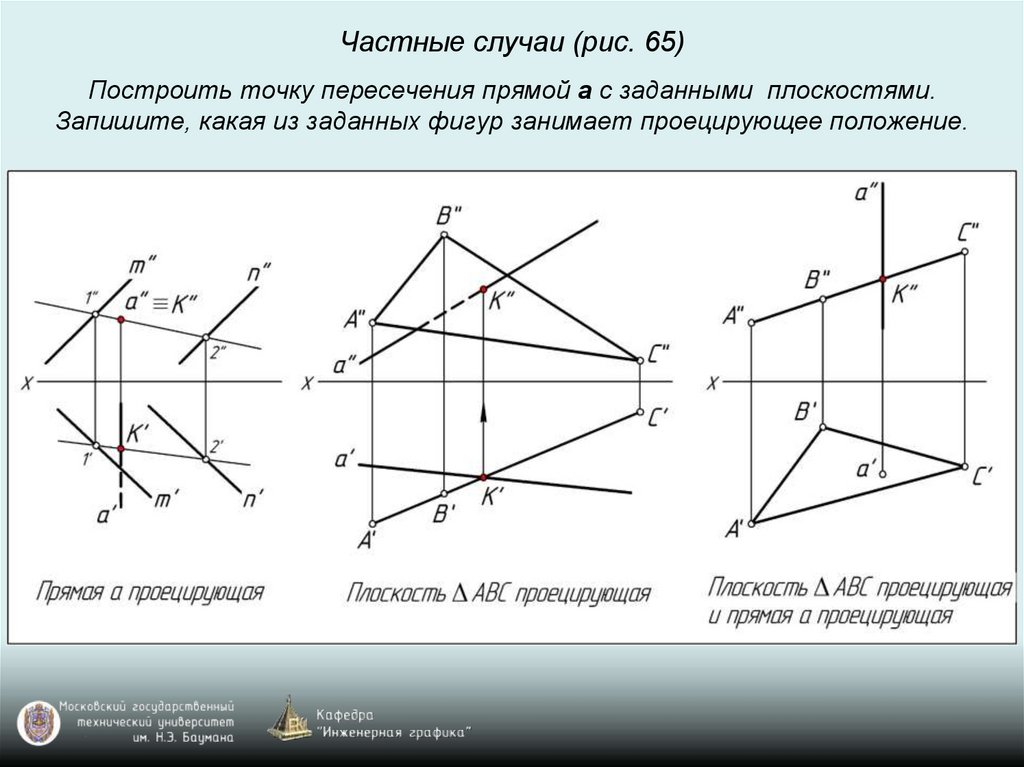
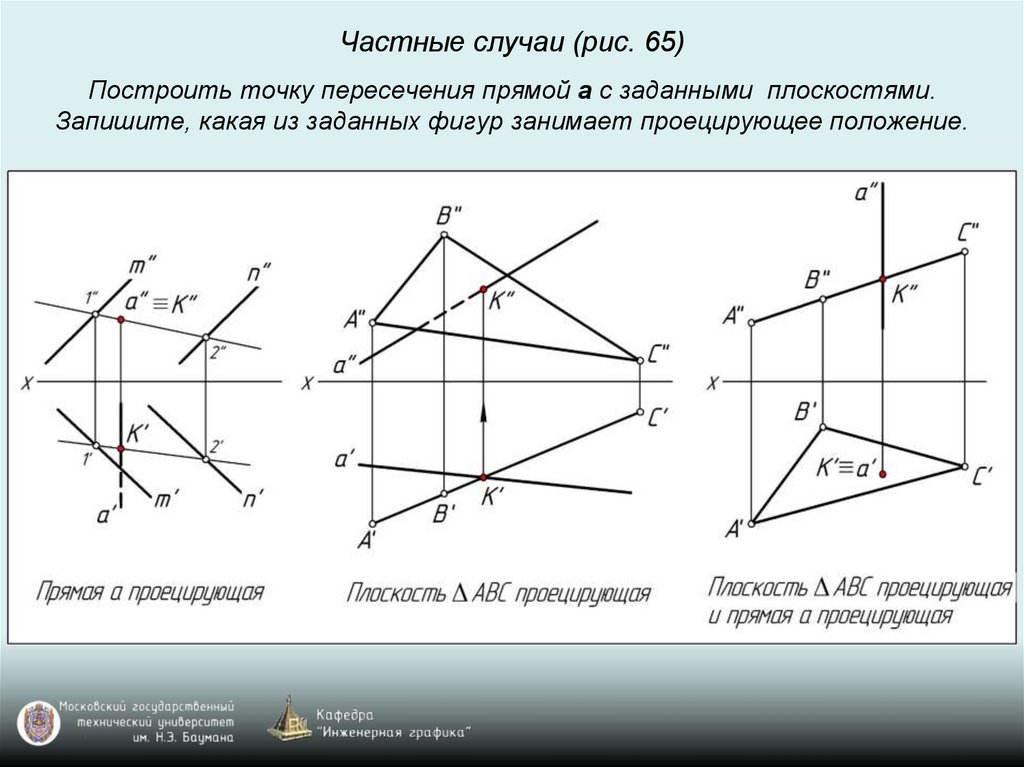
Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

20.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

21.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

22.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

23.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

24.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

25.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

26.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

27.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

28.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

29.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

30.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

31.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

32.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

33.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

34.

Частные случаи (рис. 65)
Построить точку пересечения прямой a с заданными плоскостями.
Запишите, какая из заданных фигур занимает проецирующее положение.

35.

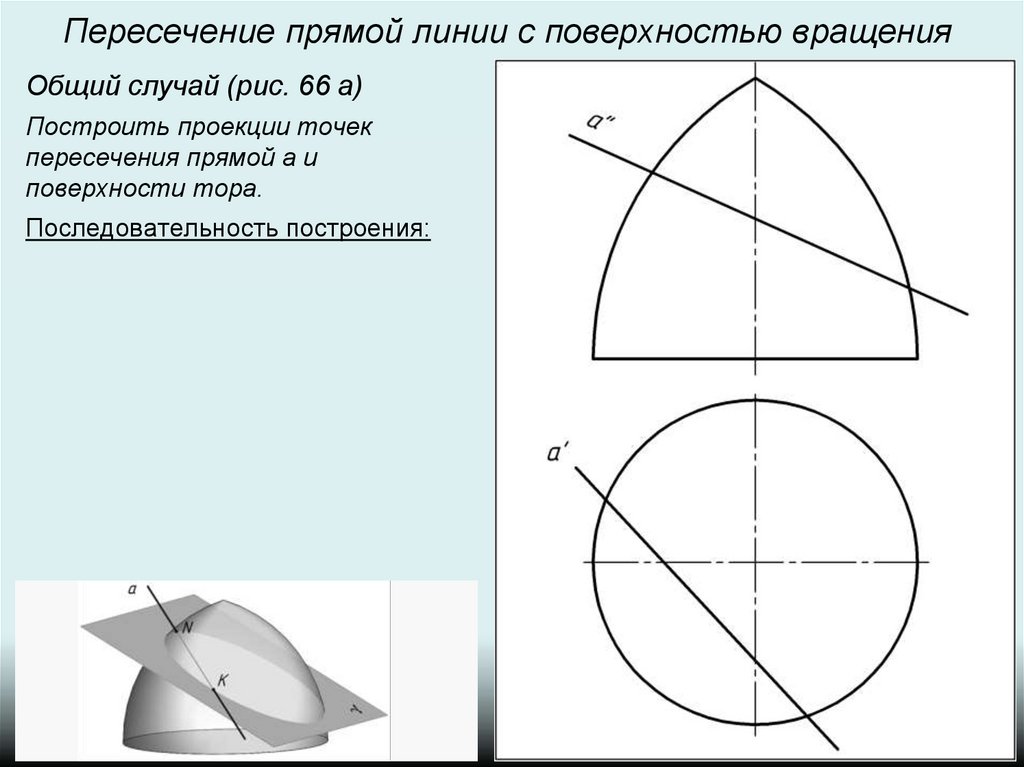
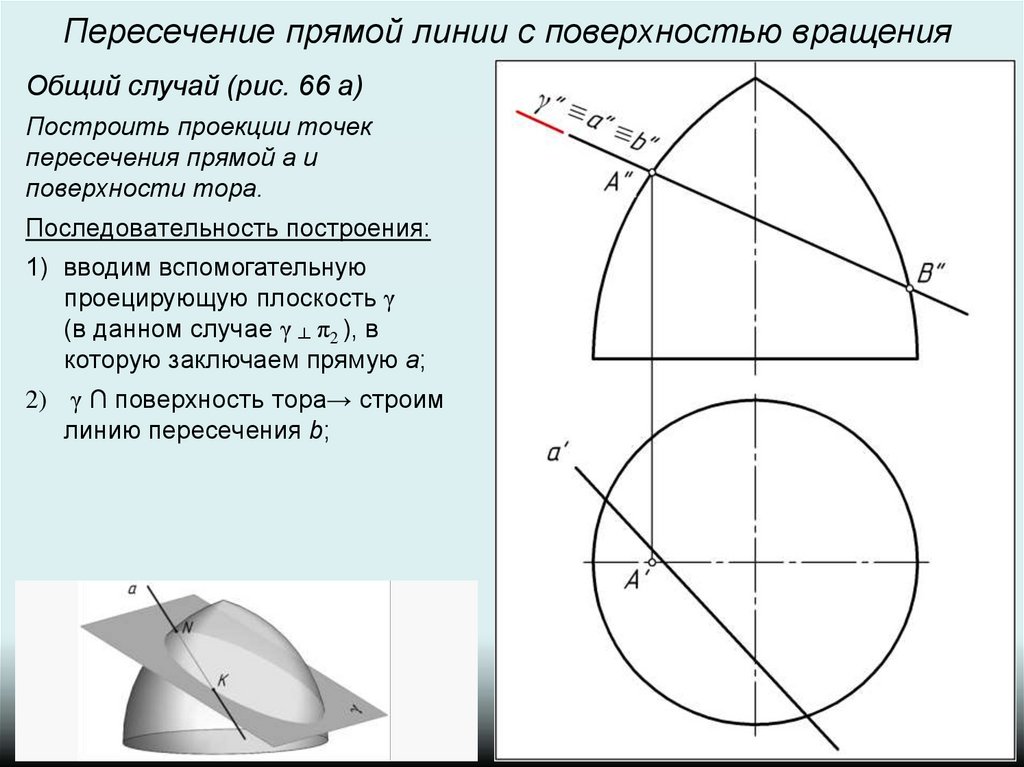
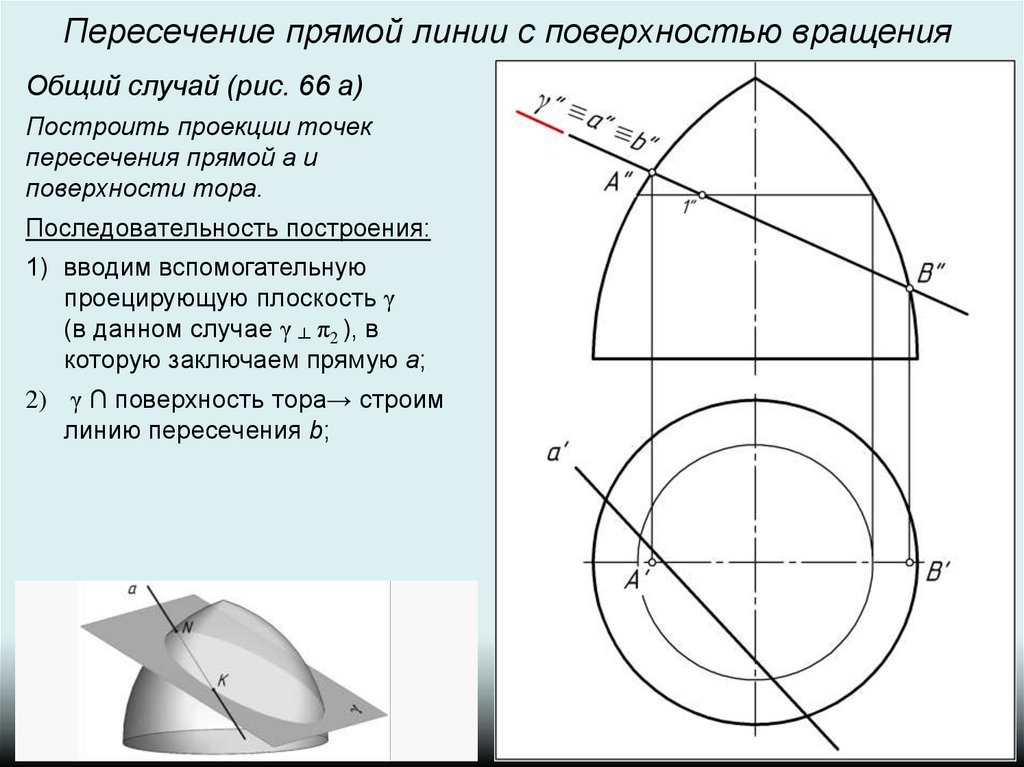
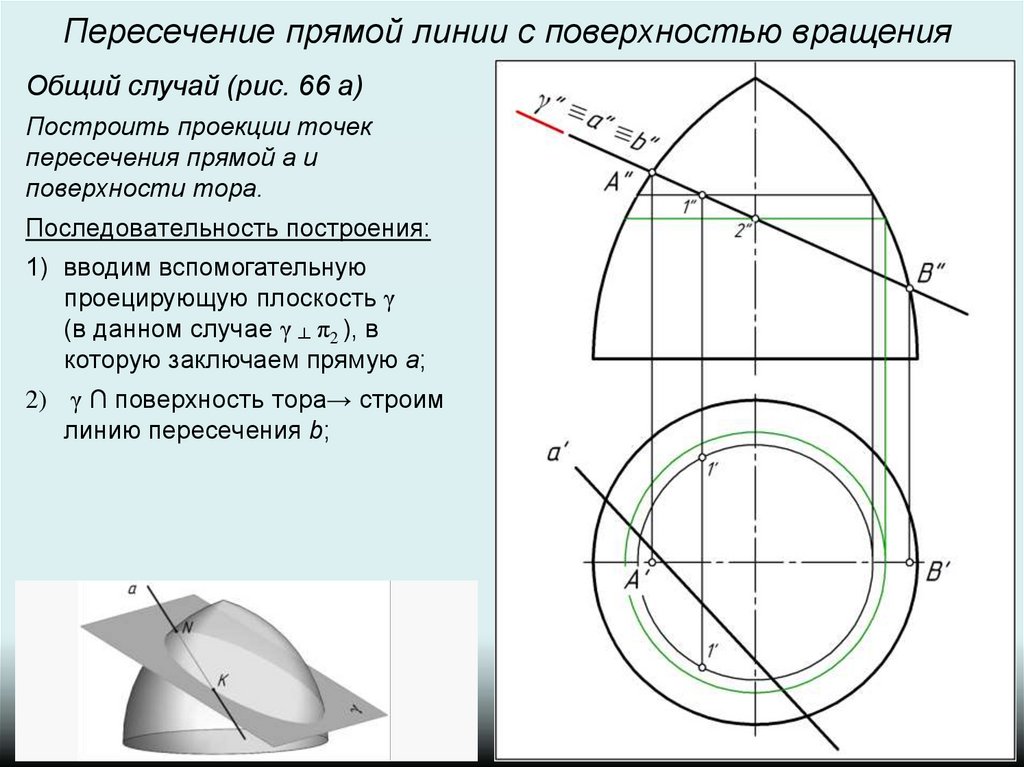
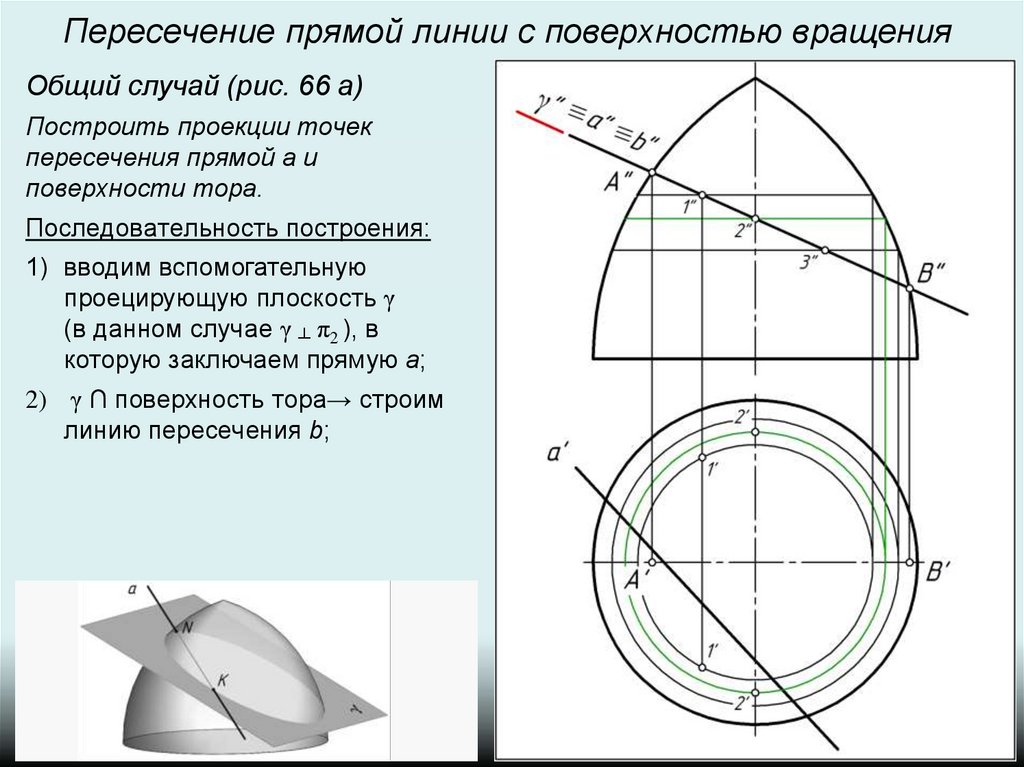
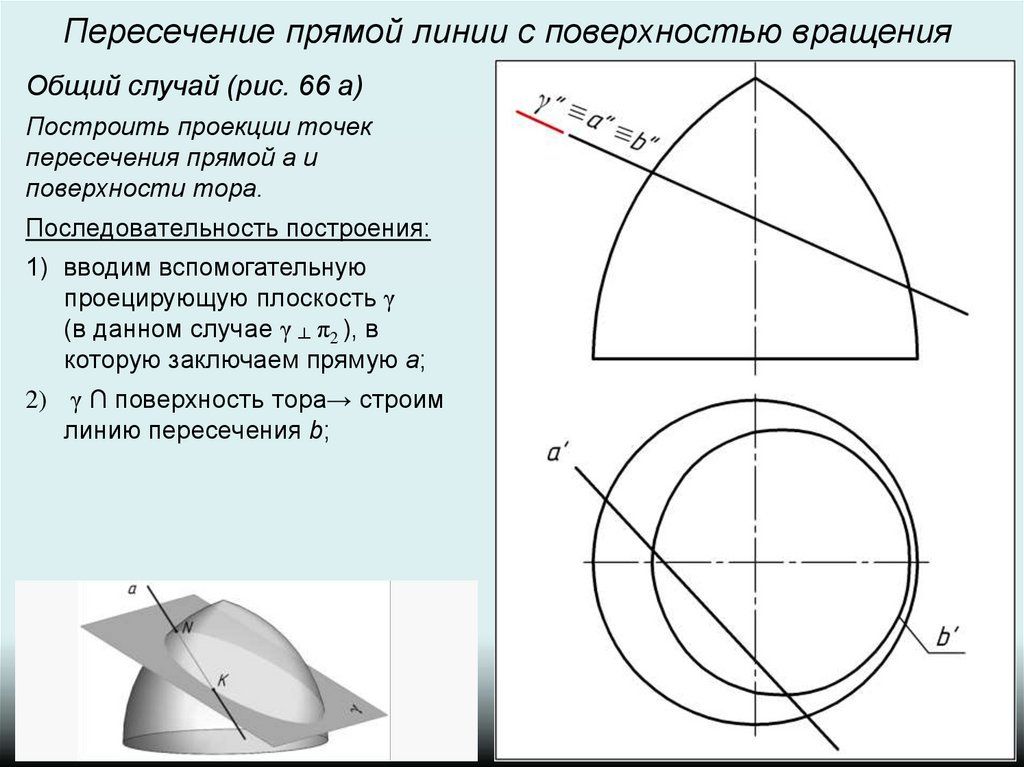
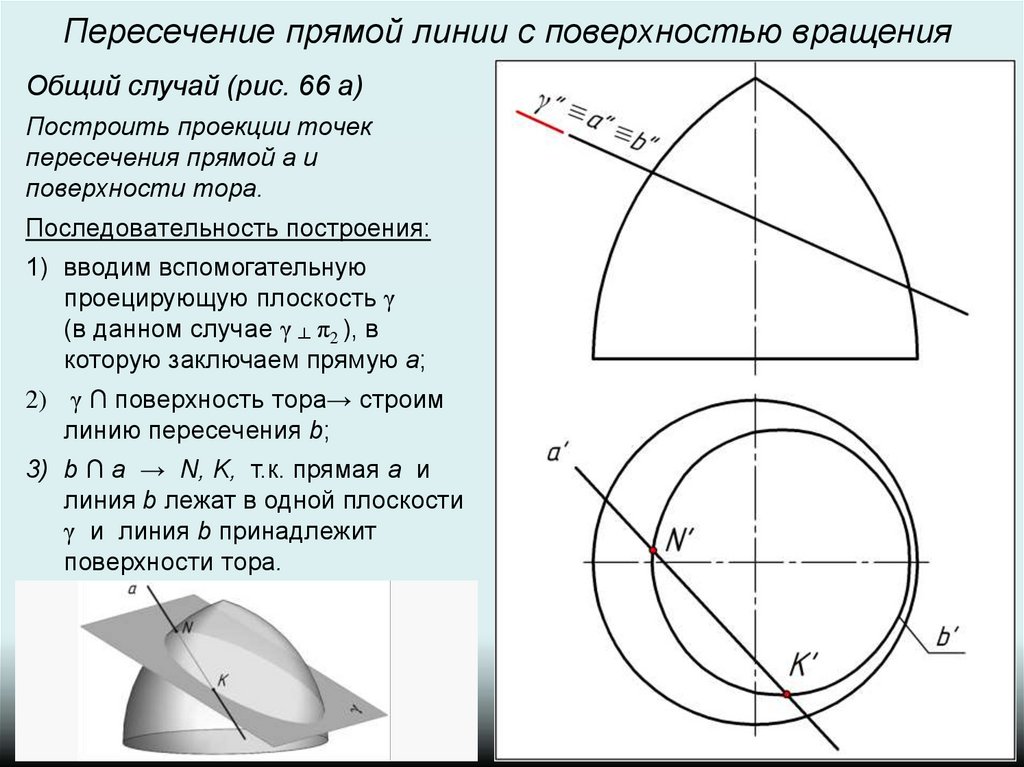
Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:

36.

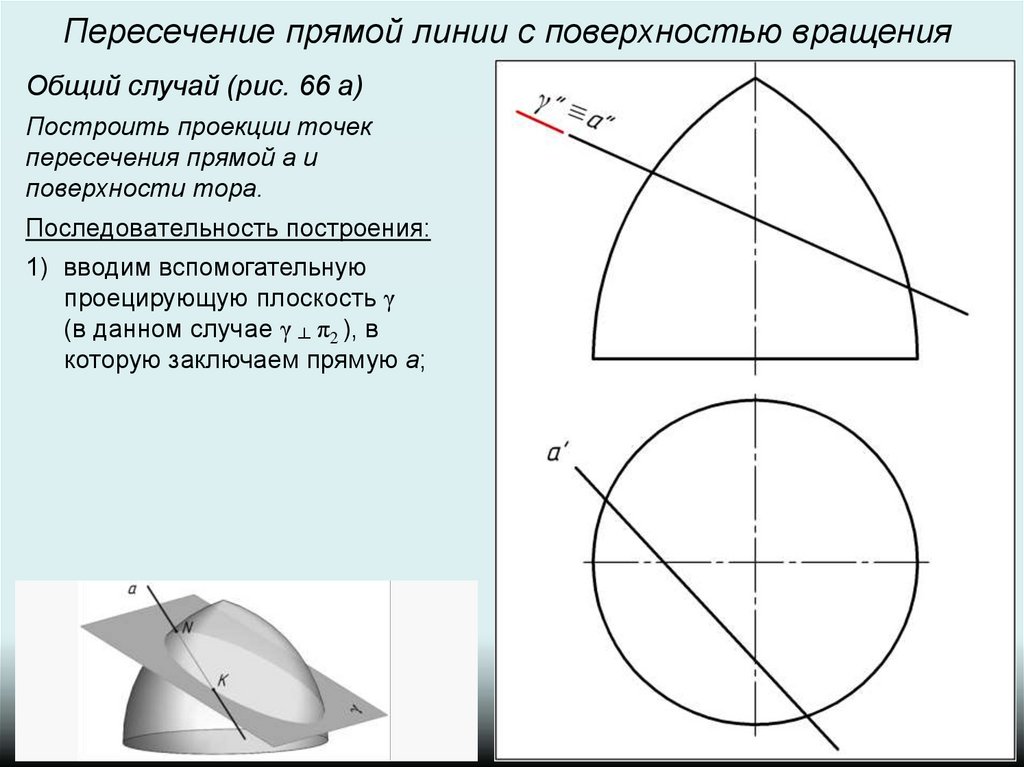
Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;

37.

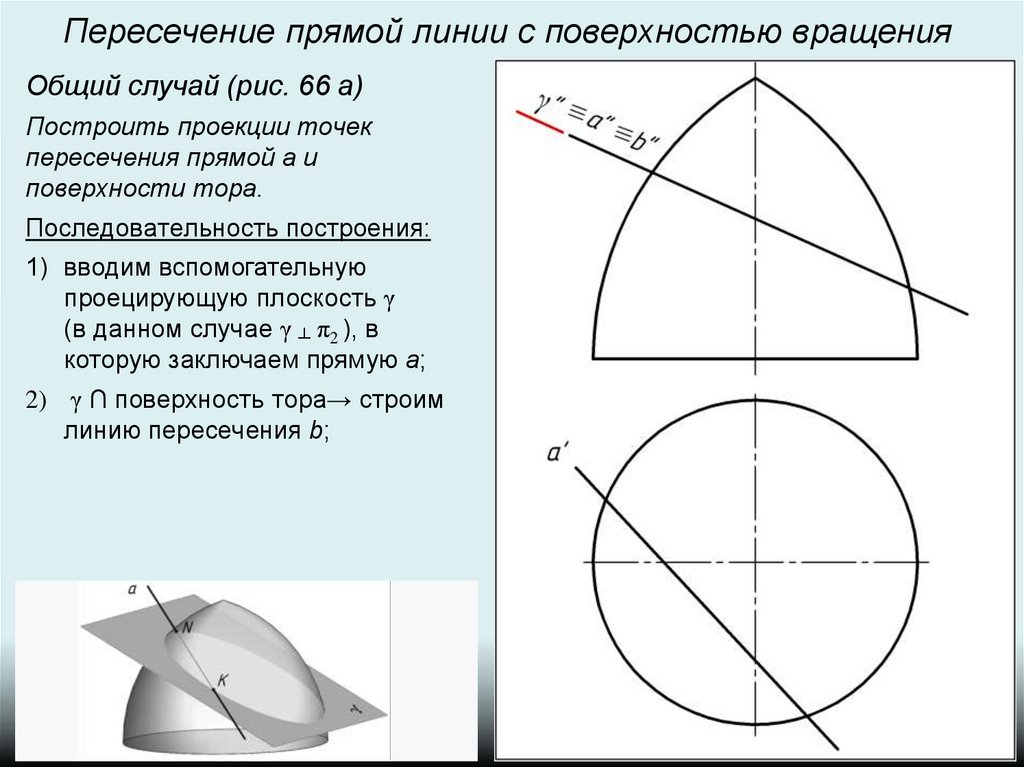
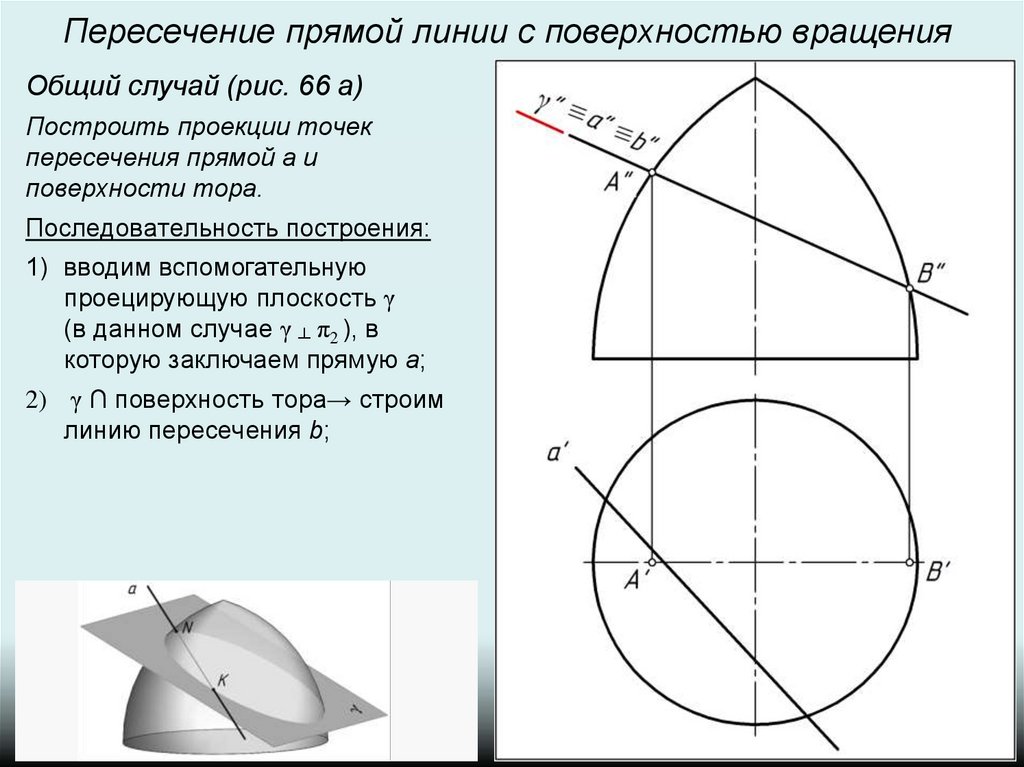
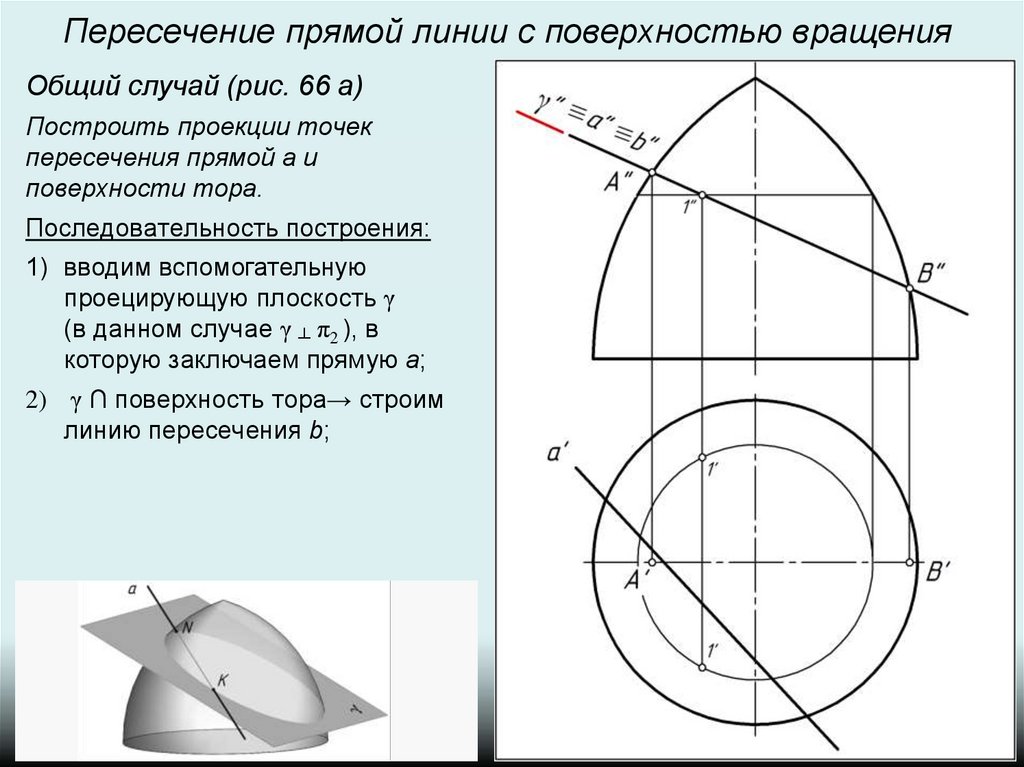
Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
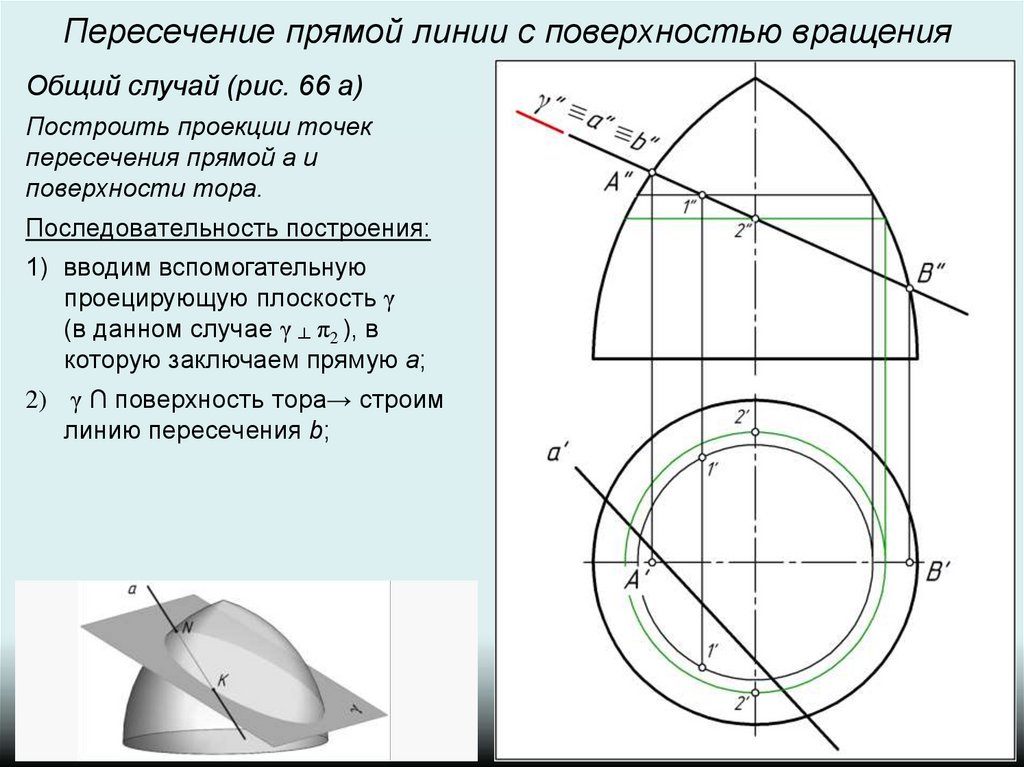
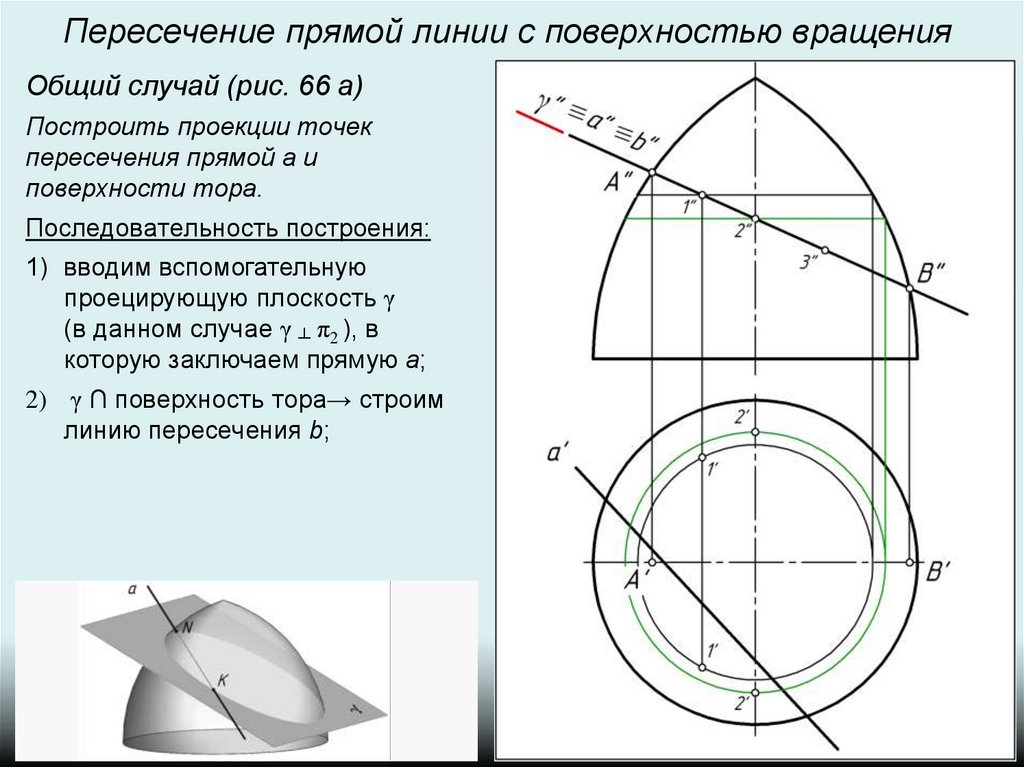
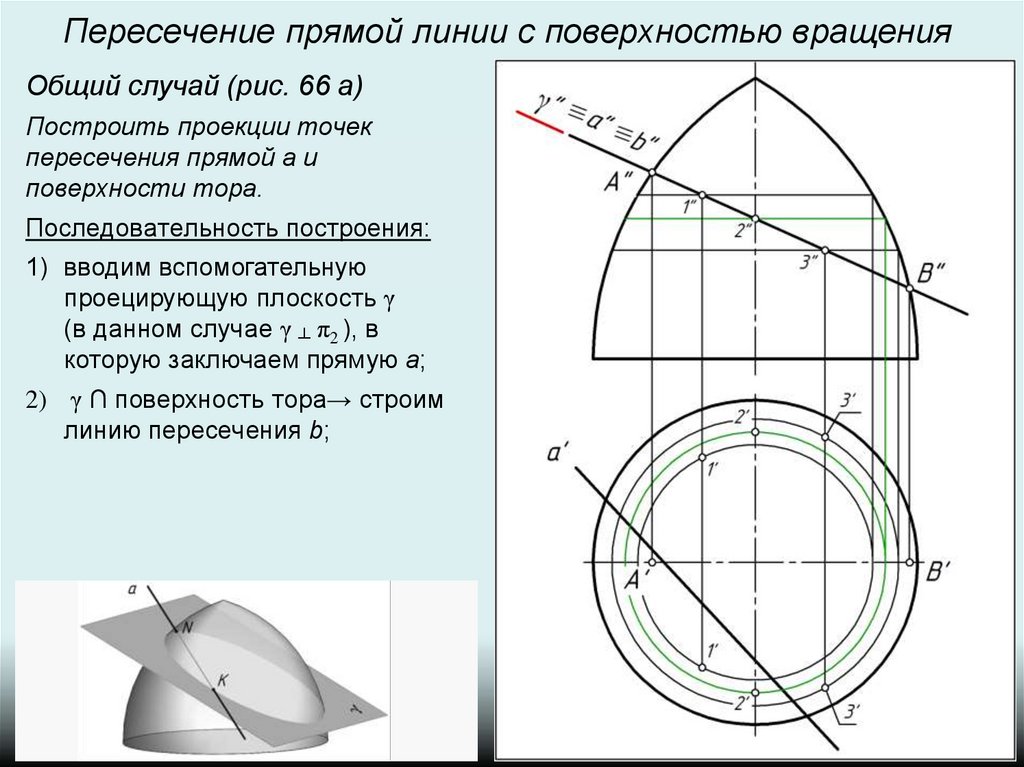
2) γ ∩ поверхность тора→ строим
линию пересечения b;

38.

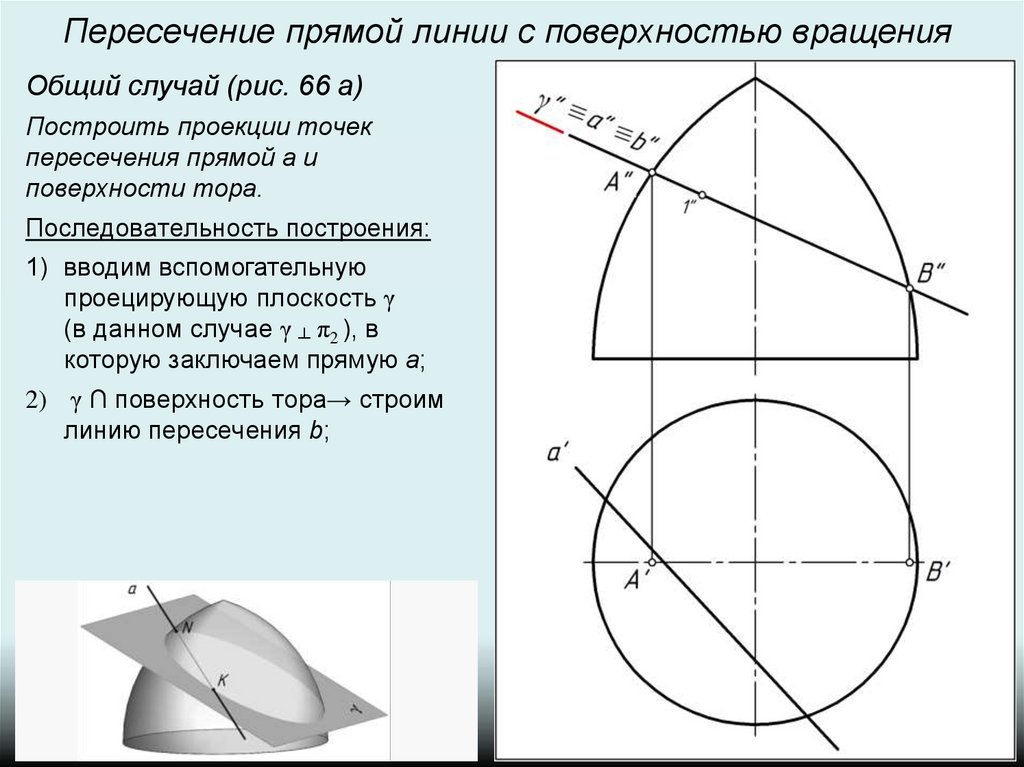
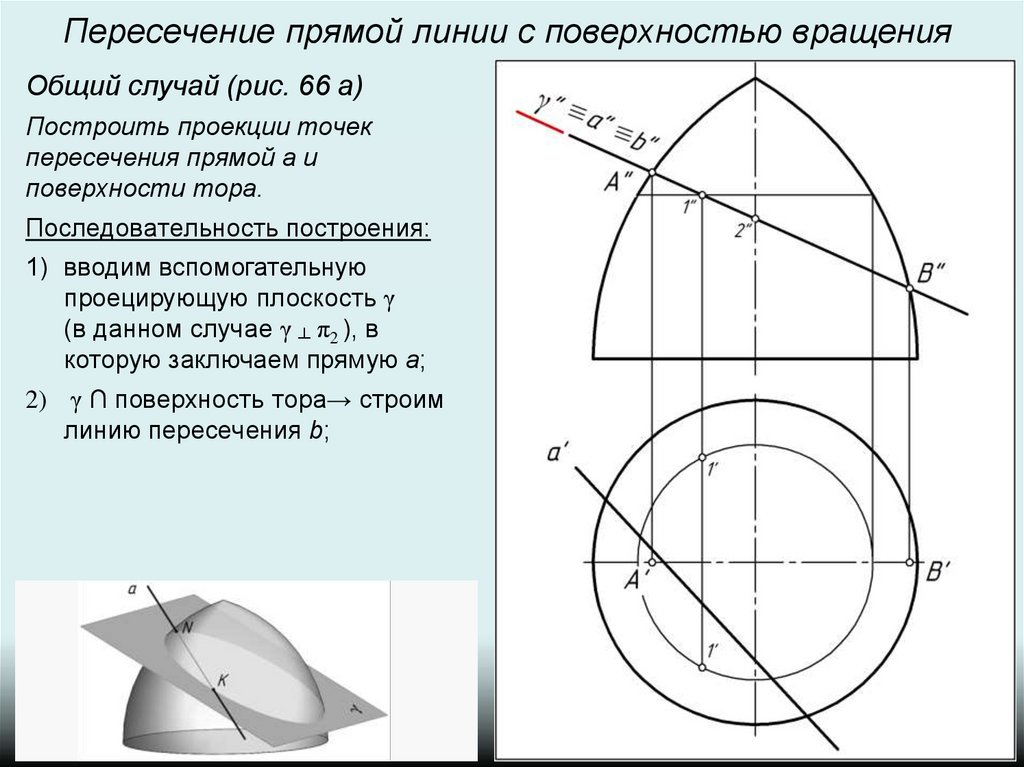
Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

39.

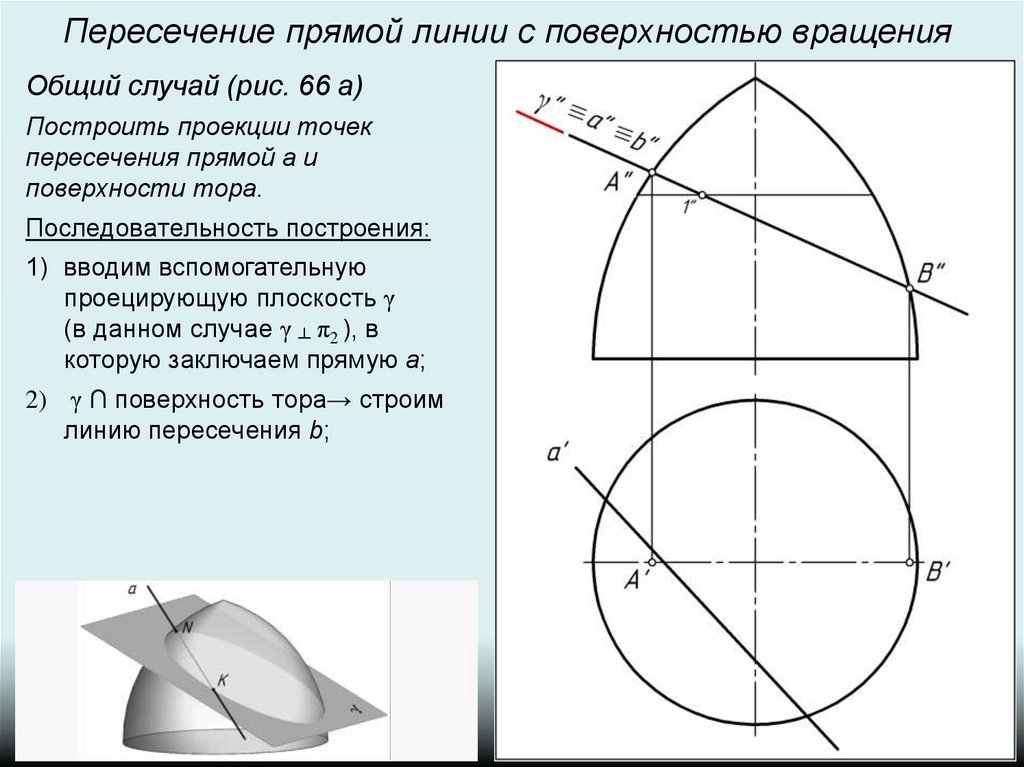
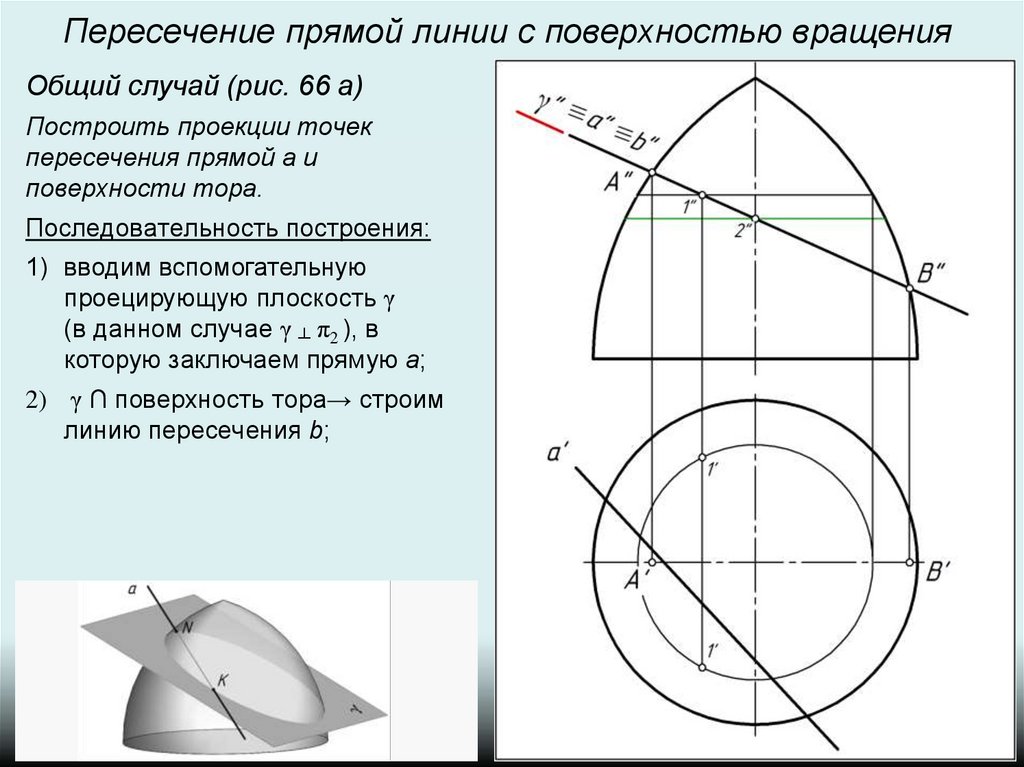
Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
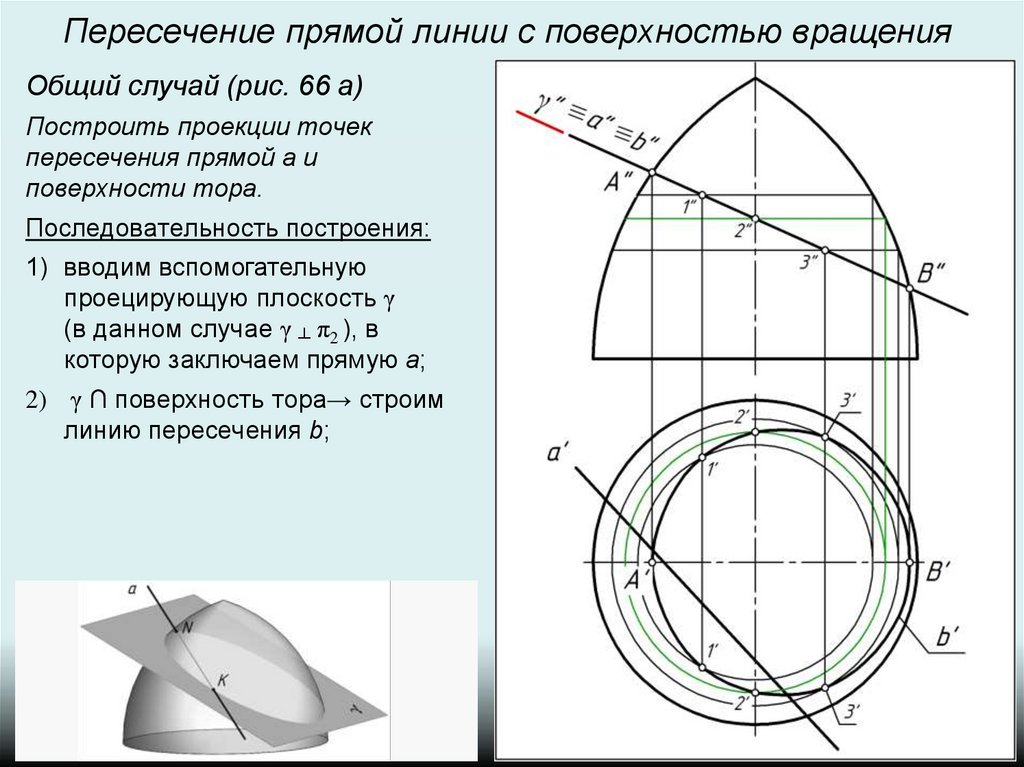
2) γ ∩ поверхность тора→ строим
линию пересечения b;

40.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

41.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

42.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

43.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

44.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

45.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

46.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

47.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

48.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

49.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

50.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

51.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

52.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

53.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

54.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;

55.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;
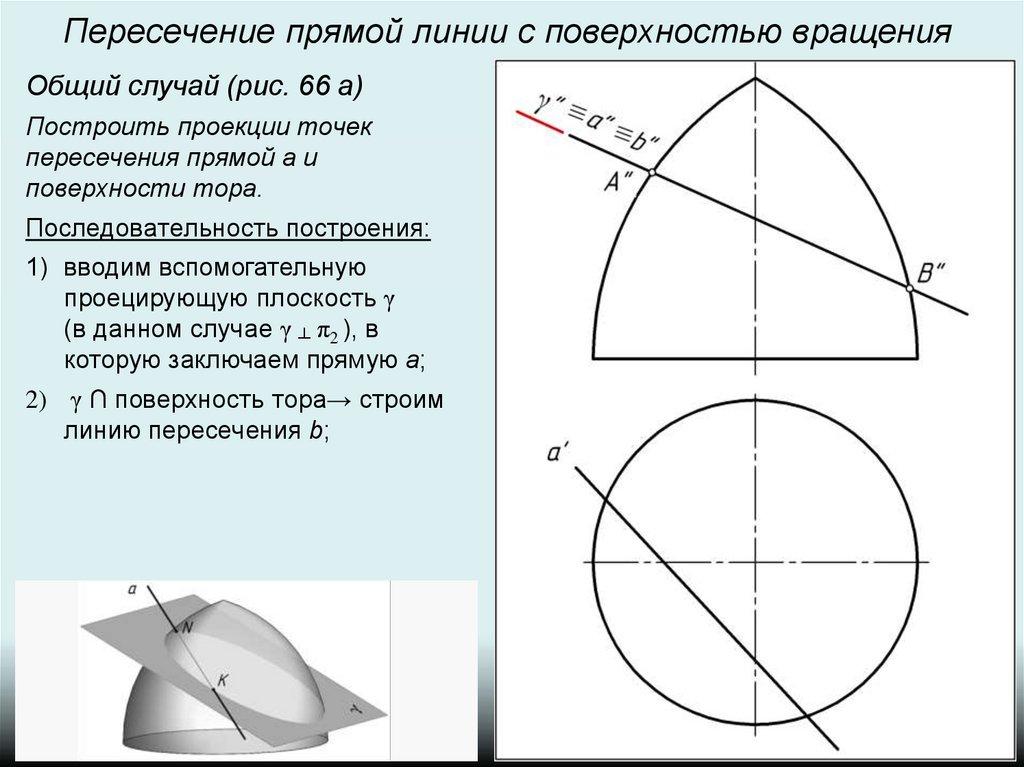
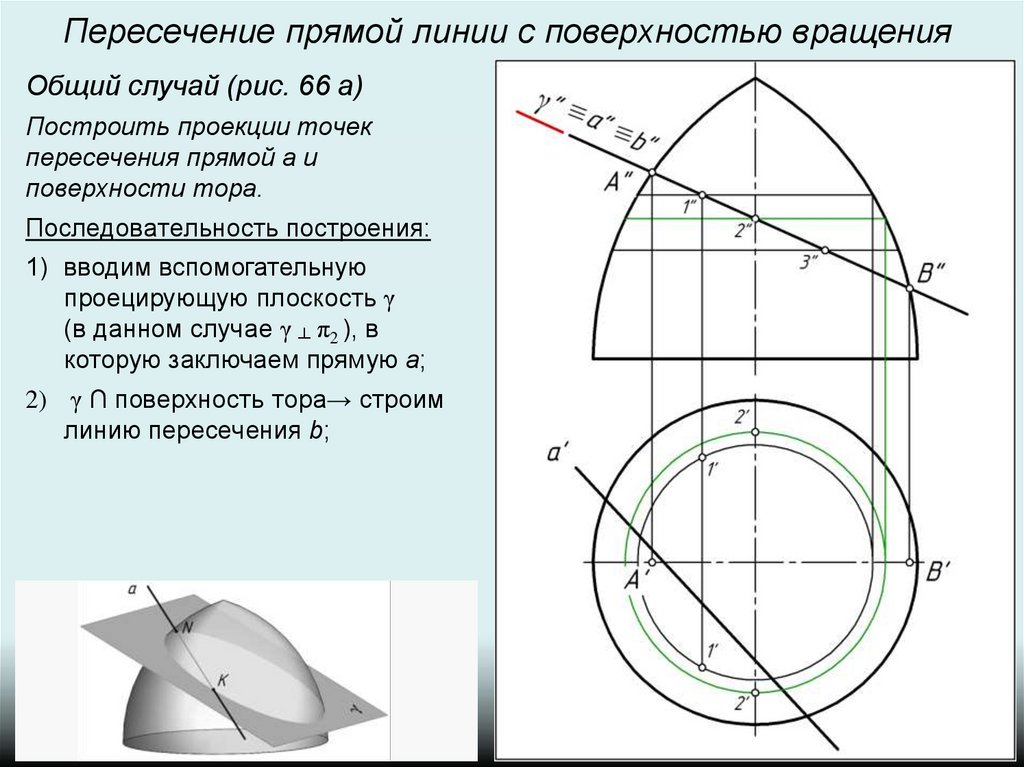
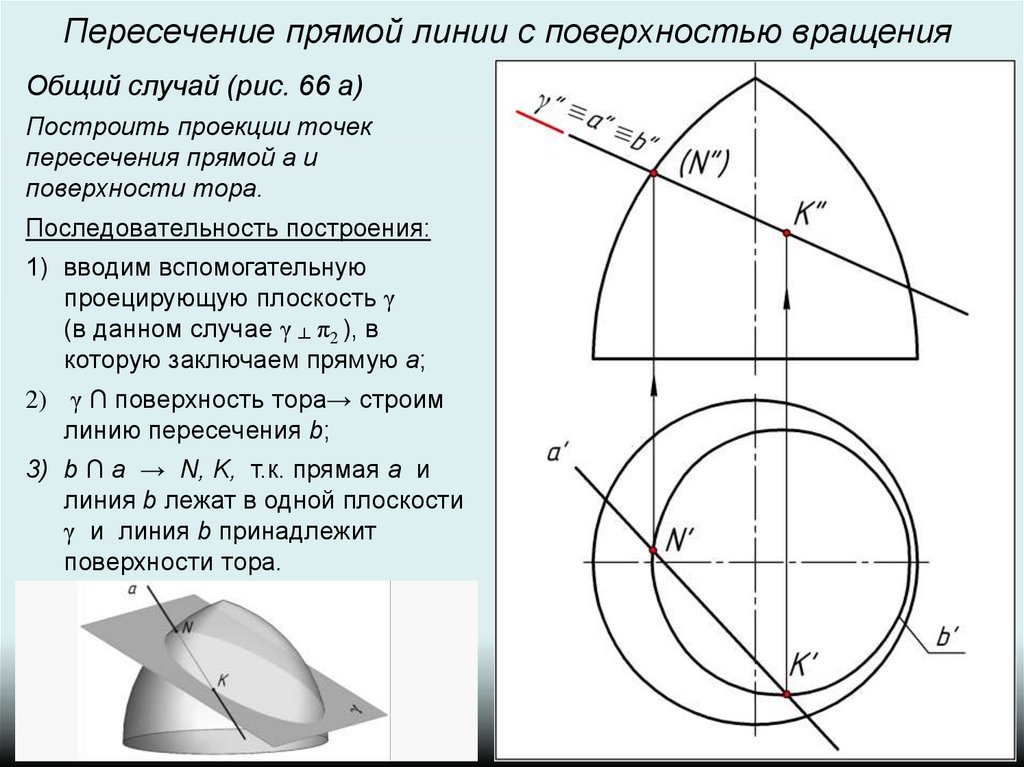
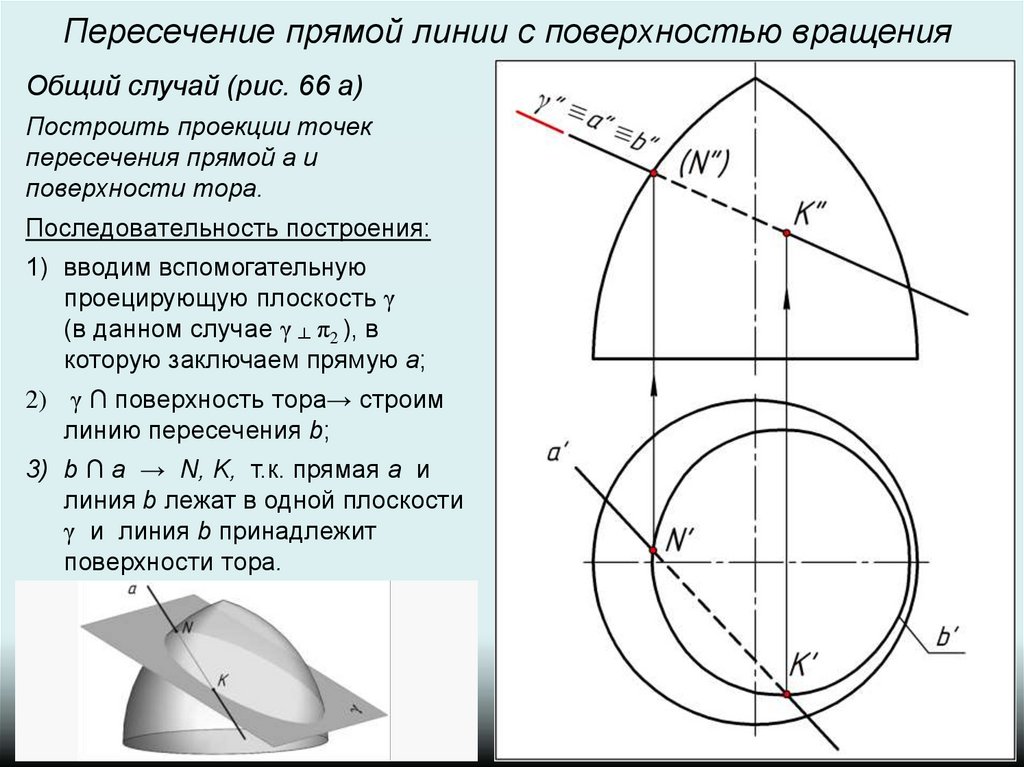
3) b ∩ a → N, K, т.к. прямая a и
линия b лежат в одной плоскости
γ и линия b принадлежит
поверхности тора.

56.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;
3) b ∩ a → N, K, т.к. прямая a и
линия b лежат в одной плоскости
γ и линия b принадлежит
поверхности тора.

57.

Пересечение прямой линии с поверхностью вращения
Общий случай (рис. 66 а)
Построить проекции точек
пересечения прямой а и
поверхности тора.
Последовательность построения:
1) вводим вспомогательную
проецирующую плоскость γ
(в данном случае γ ┴ π2 ), в
которую заключаем прямую a;
2) γ ∩ поверхность тора→ строим
линию пересечения b;
3) b ∩ a → N, K, т.к. прямая a и
линия b лежат в одной плоскости
γ и линия b принадлежит
поверхности тора.

58.

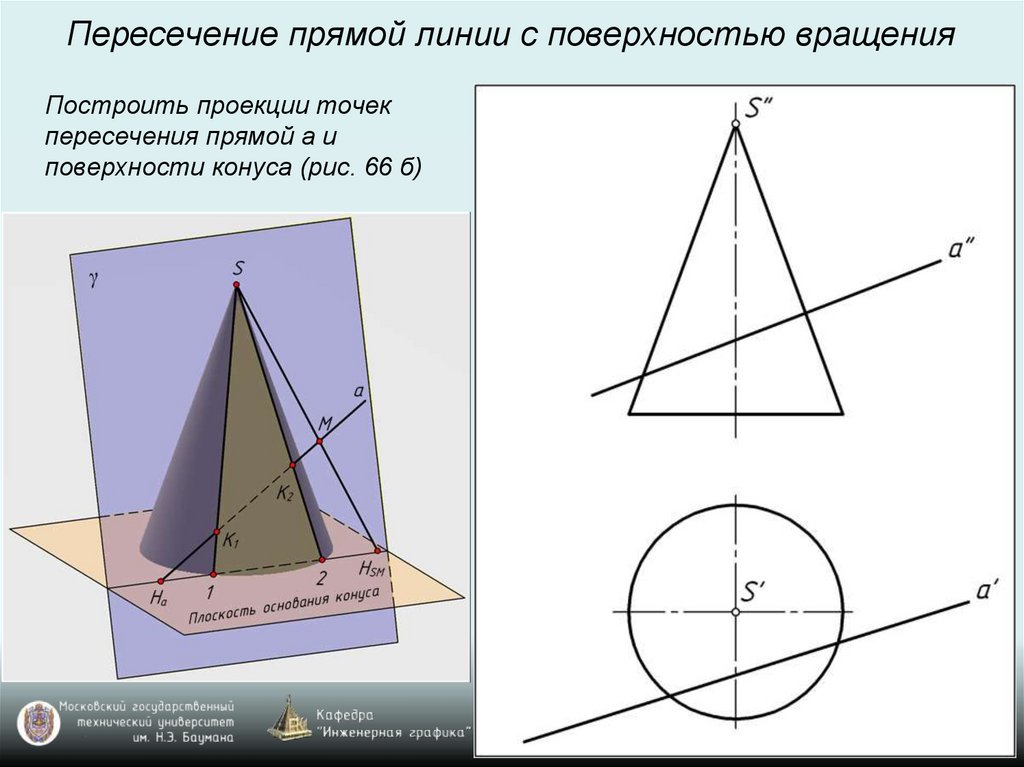
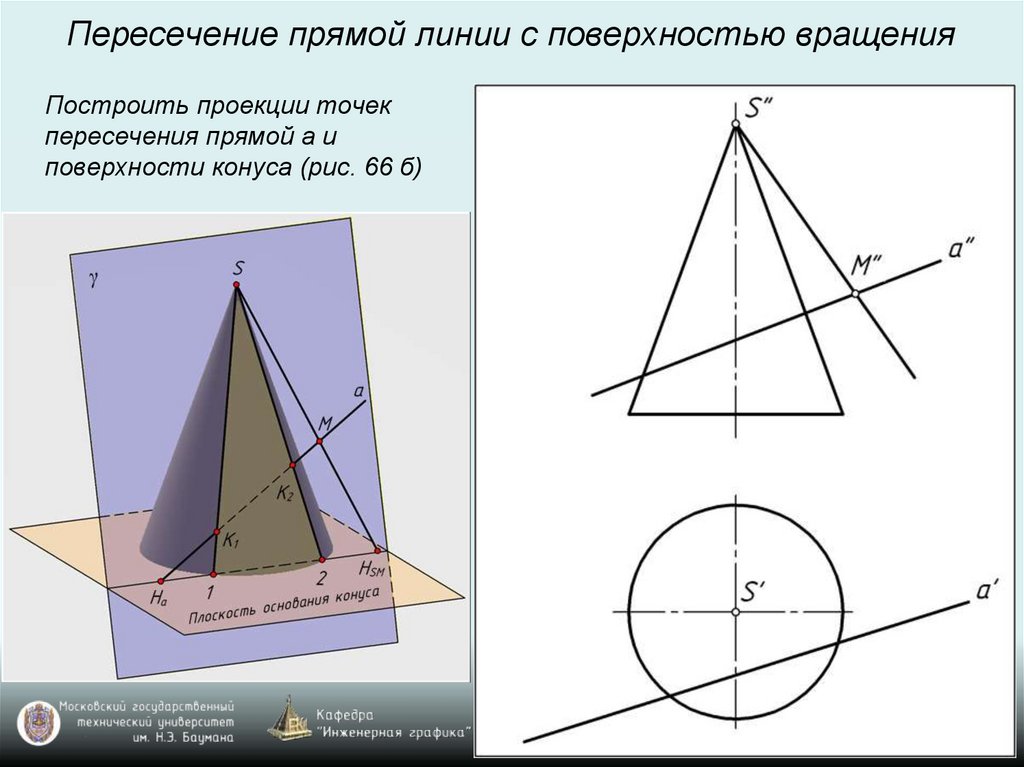
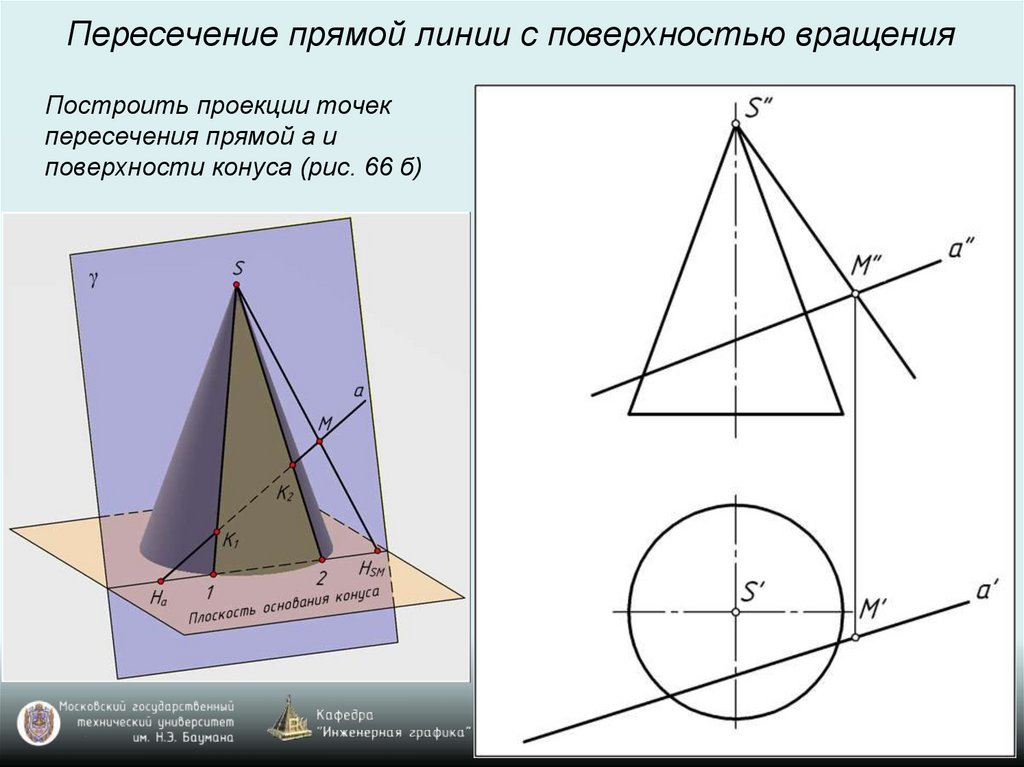
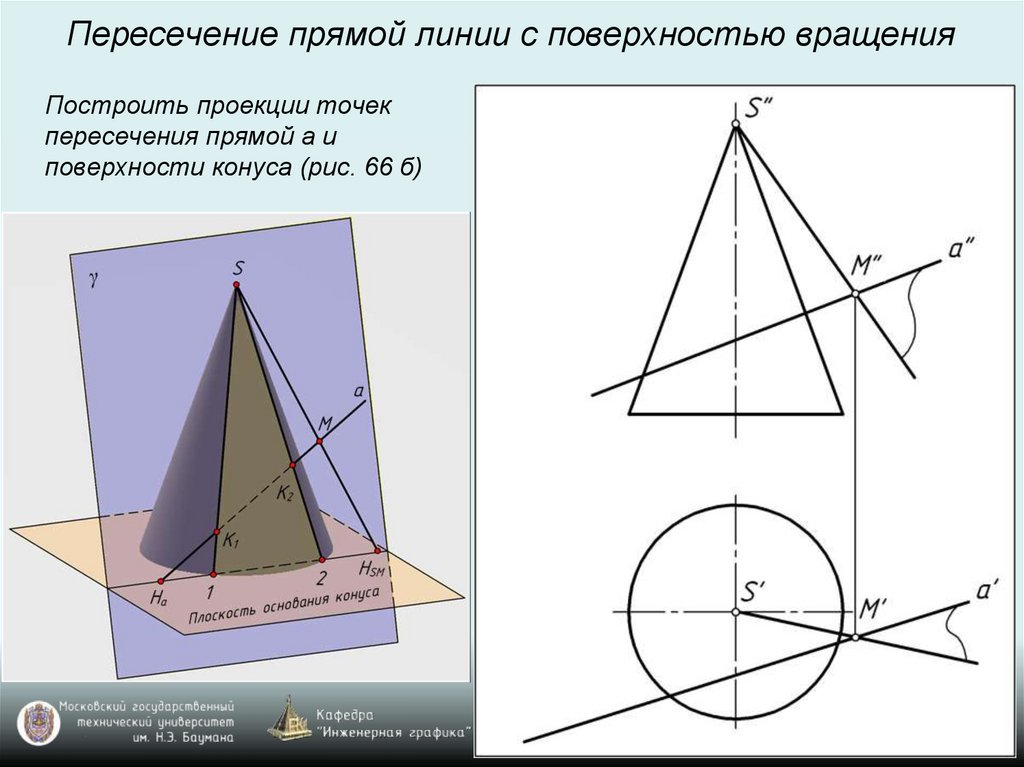
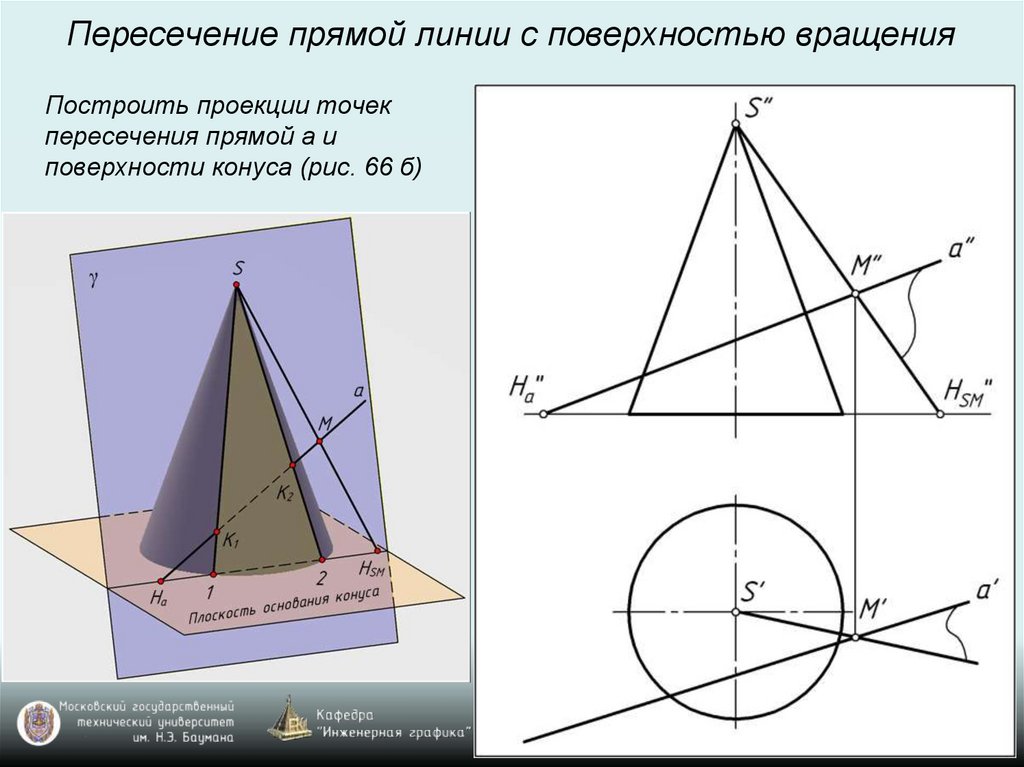
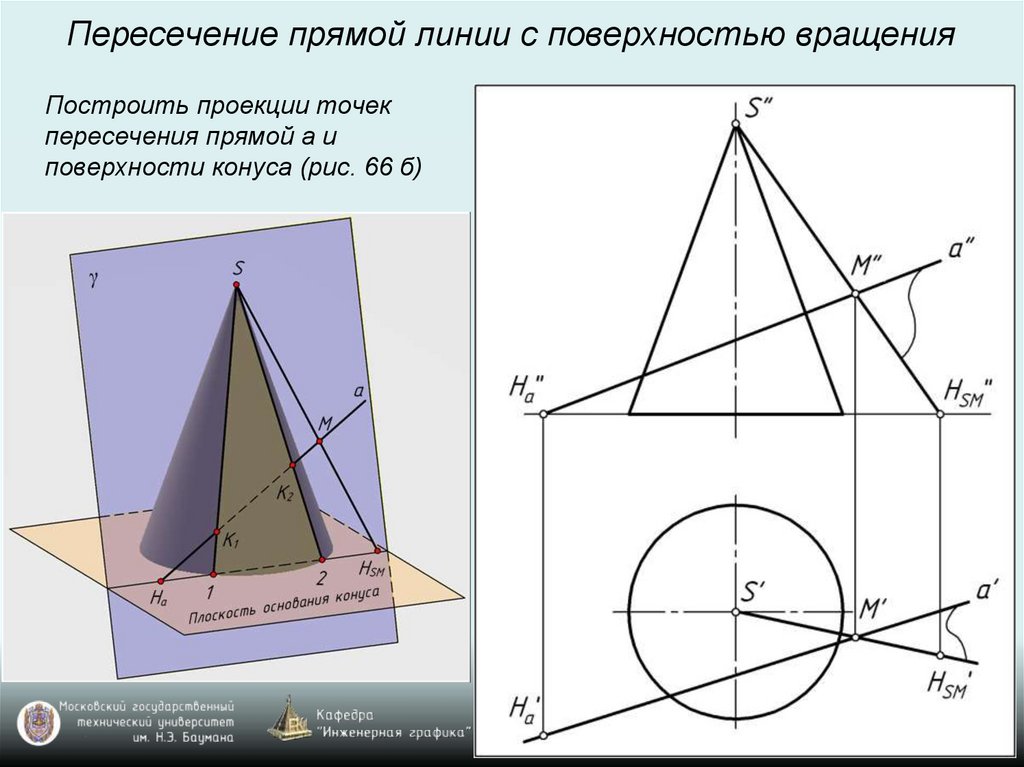
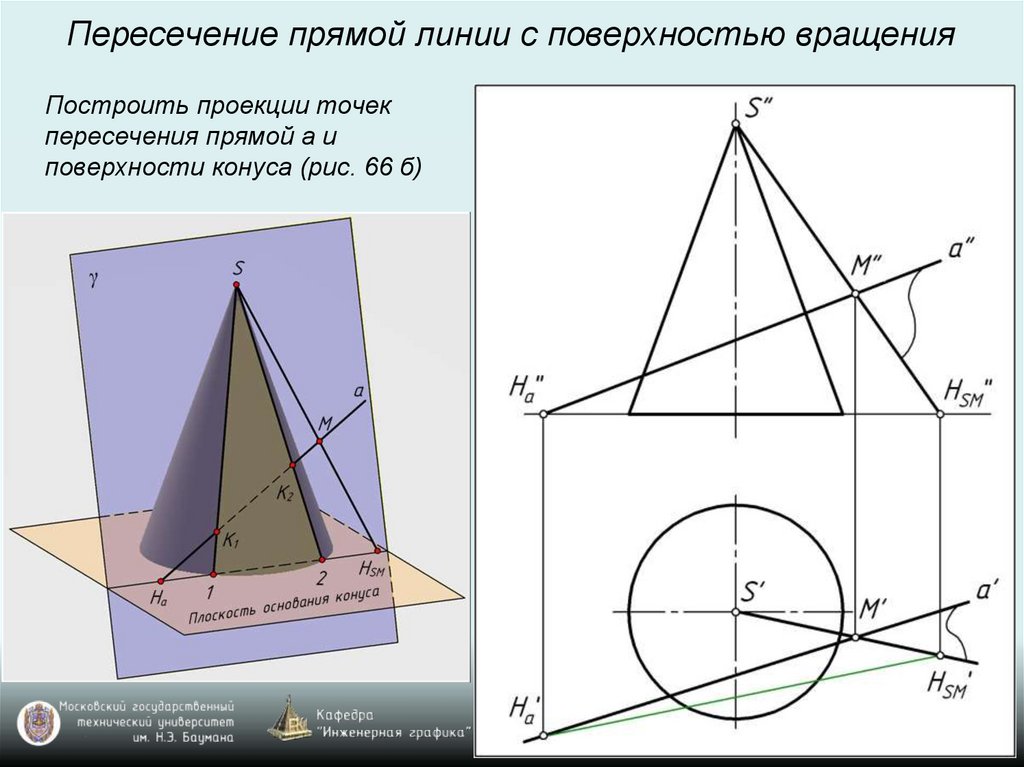
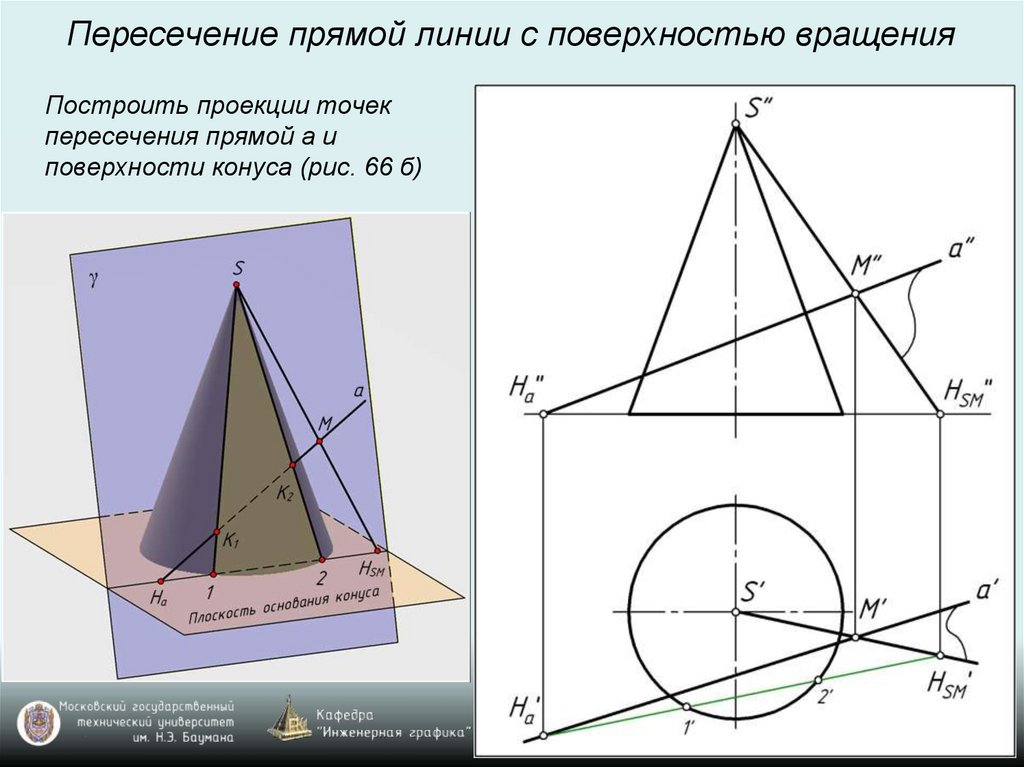
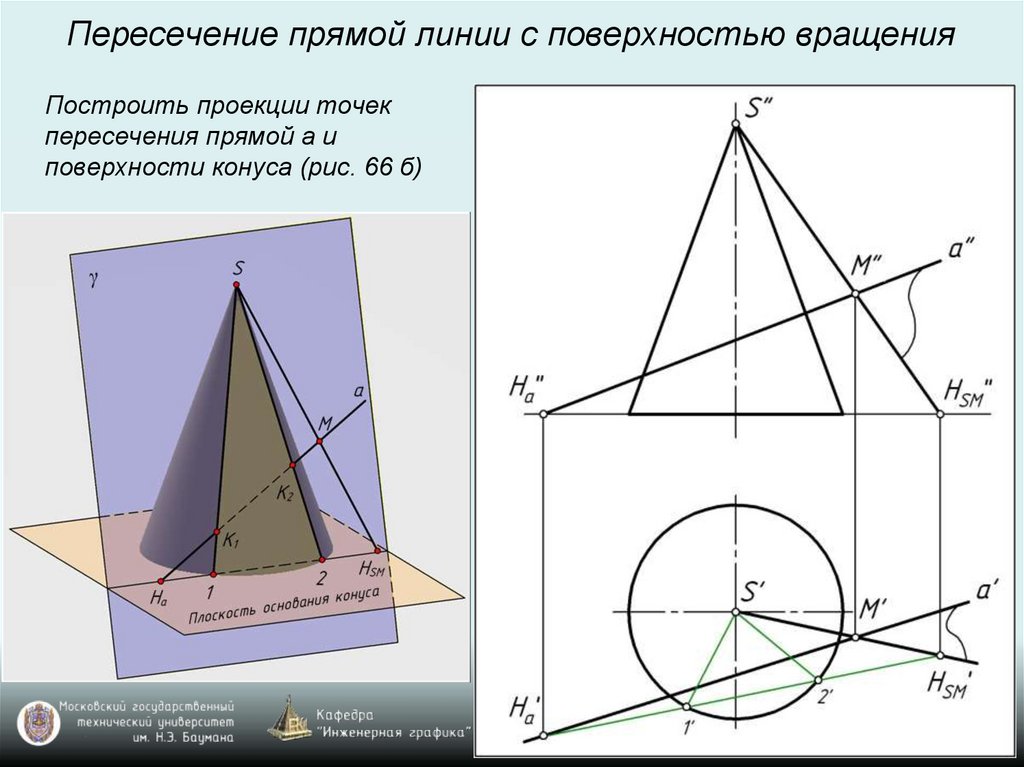
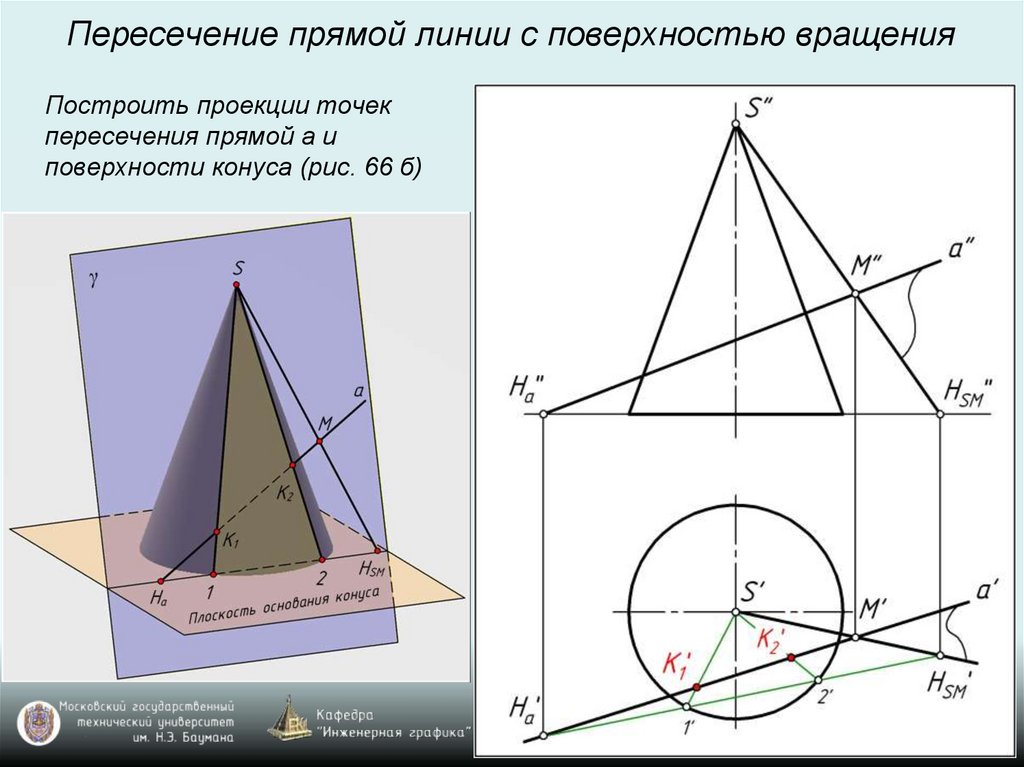
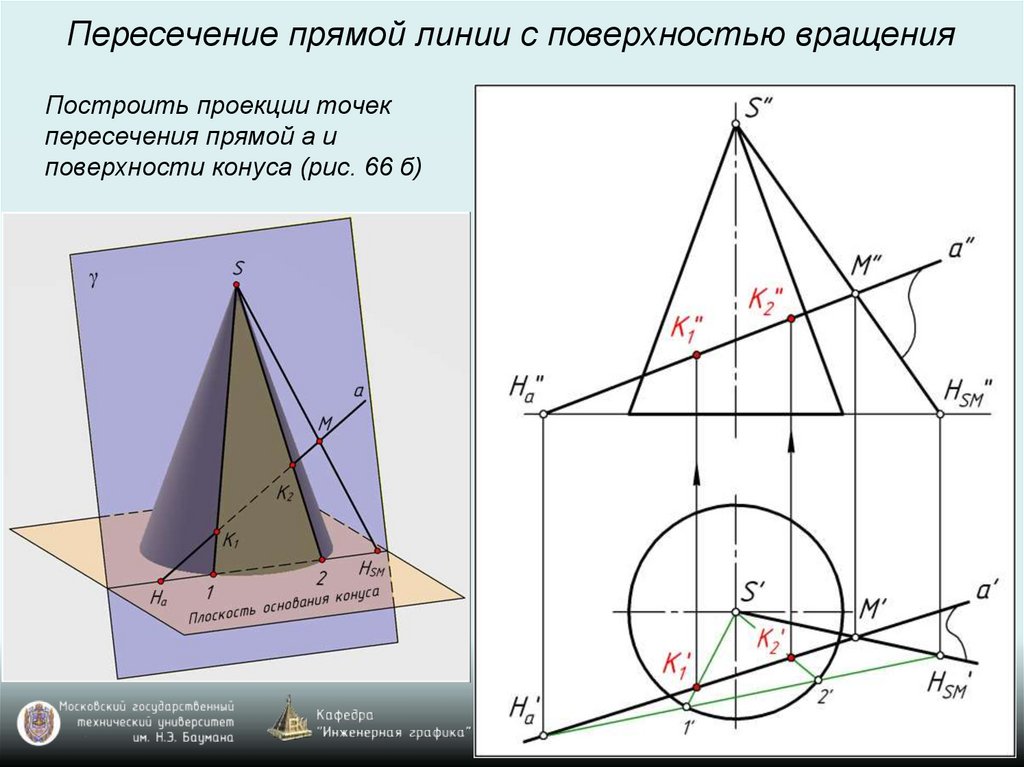
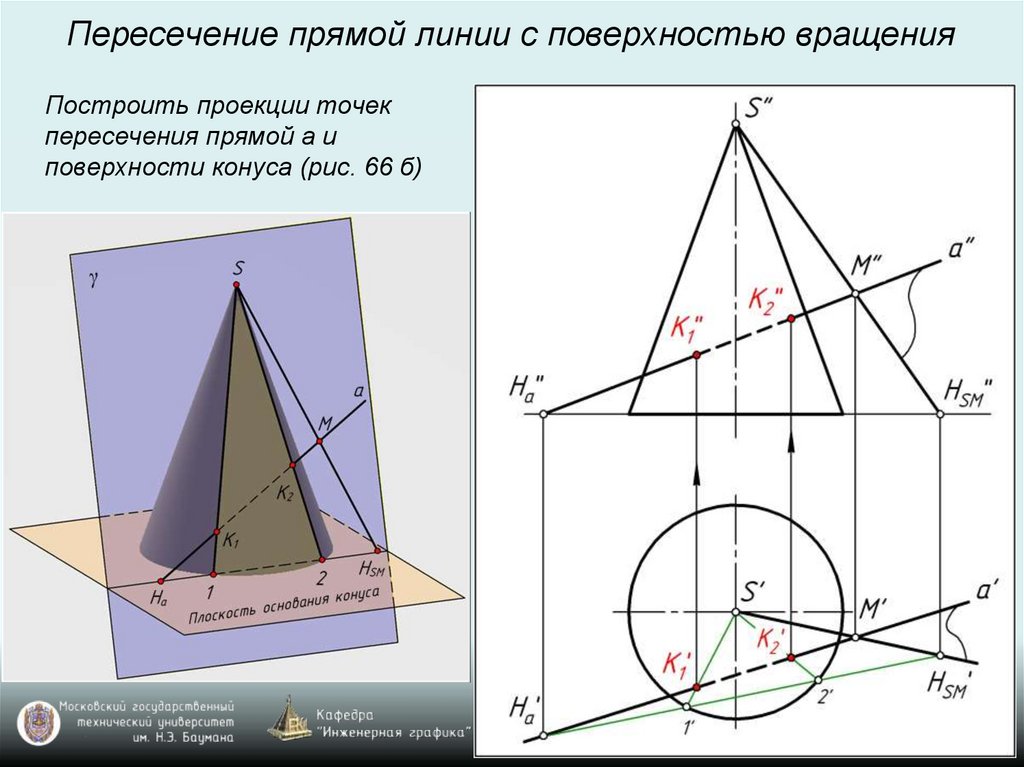
Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

59.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

60.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

61.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

62.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

63.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

64.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

65.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

66.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

67.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

68.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

69.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

70.

Пересечение прямой линии с поверхностью вращения
Построить проекции точек
пересечения прямой а и
поверхности конуса (рис. 66 б)

71.

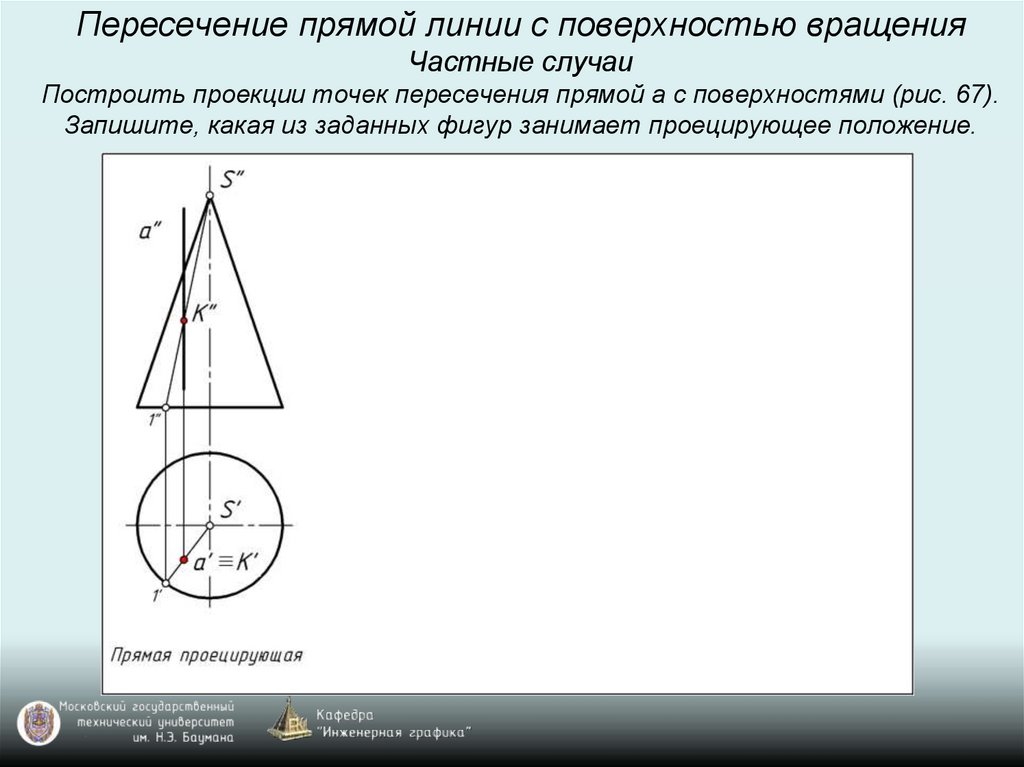
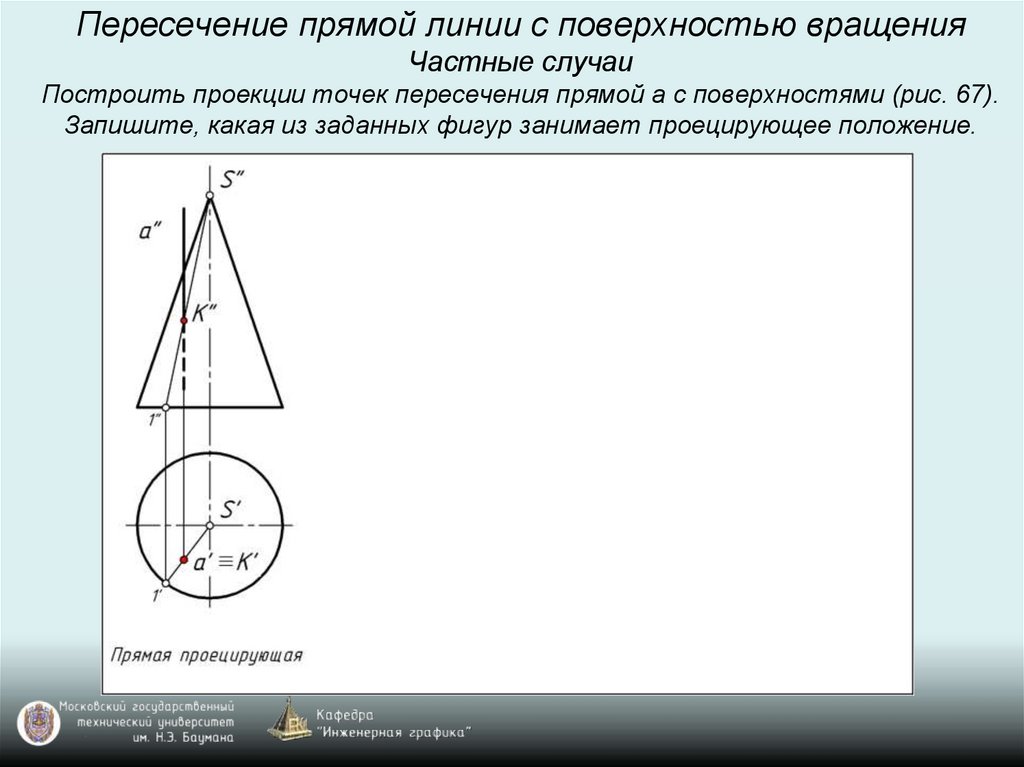
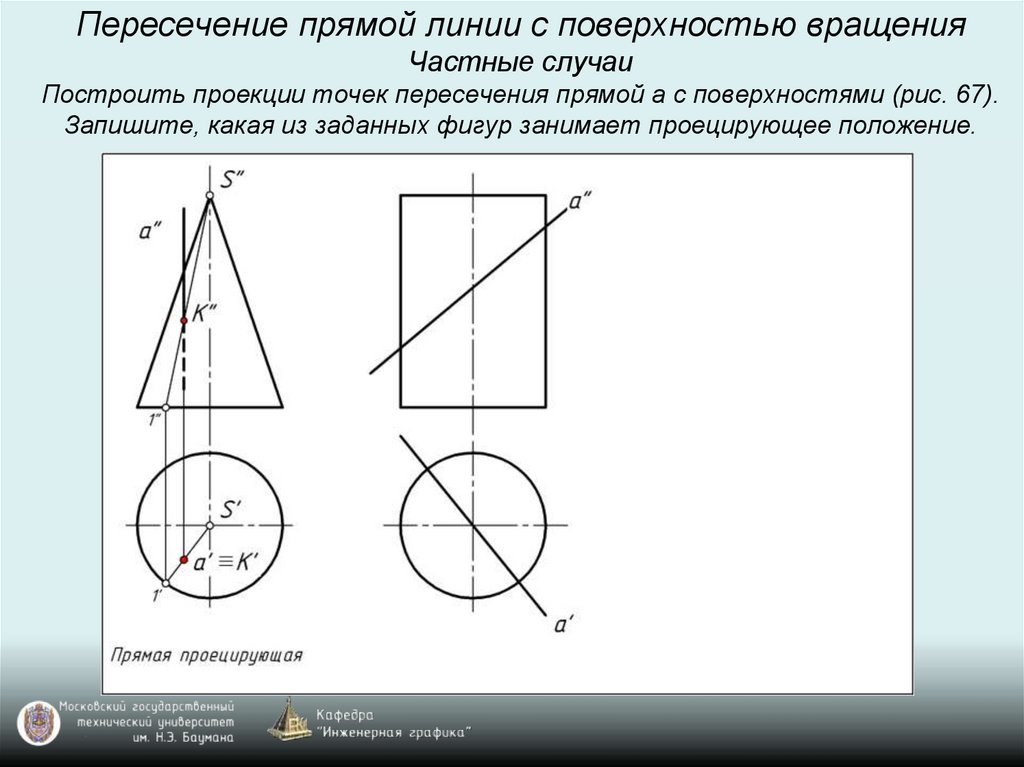
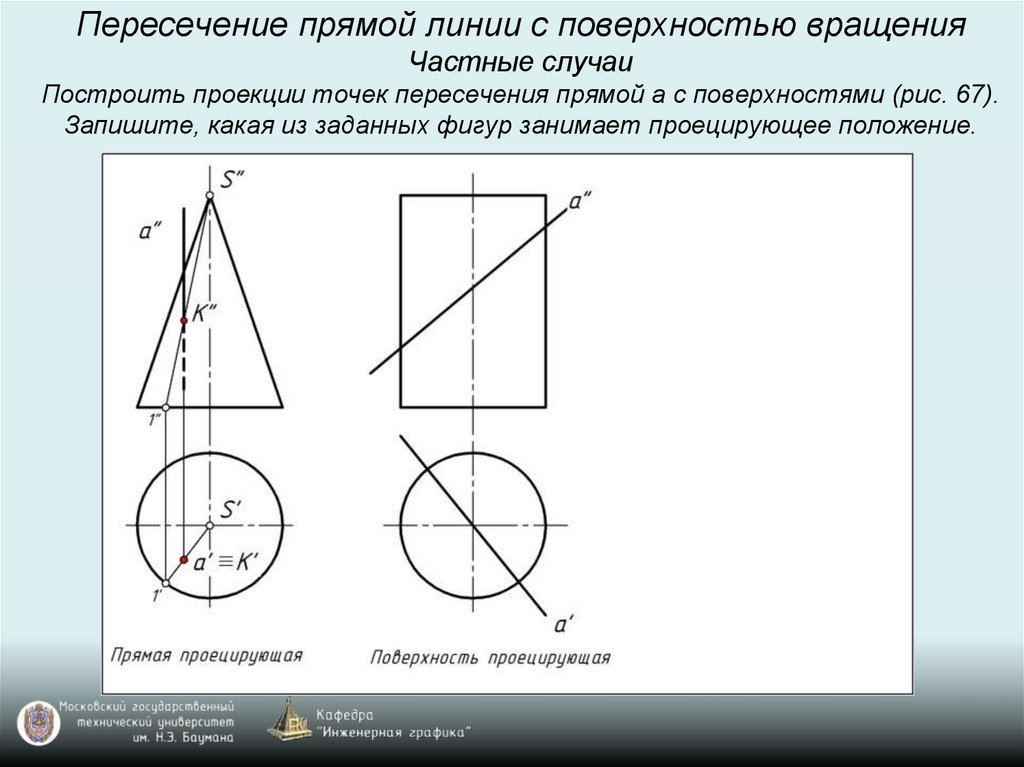
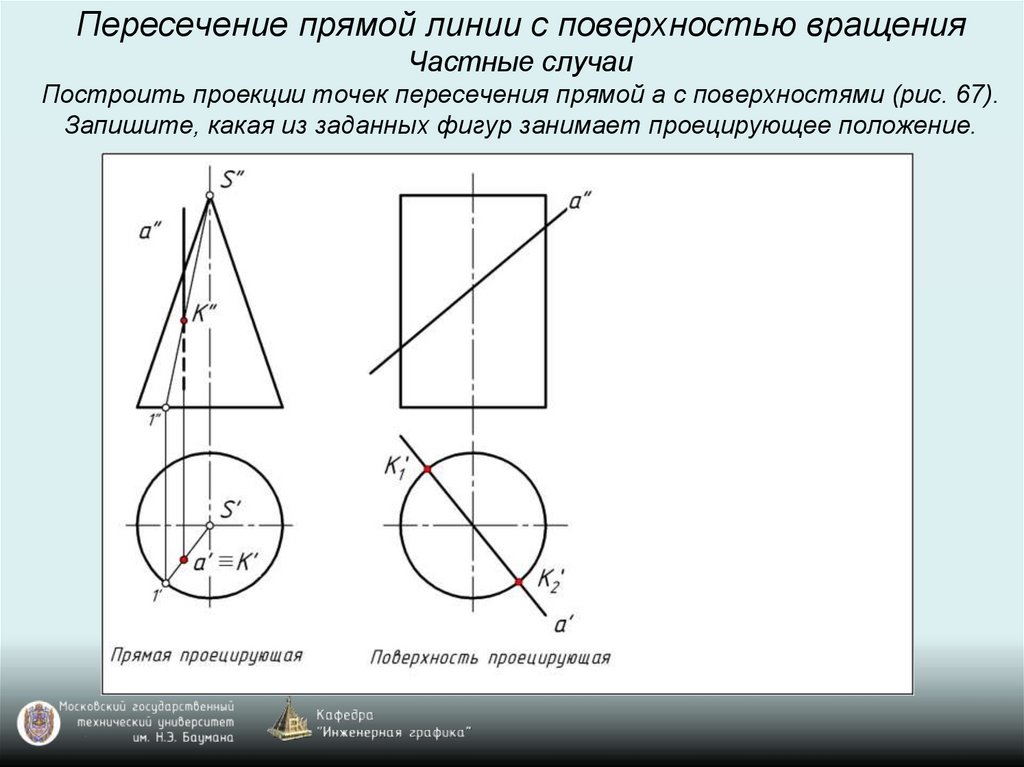
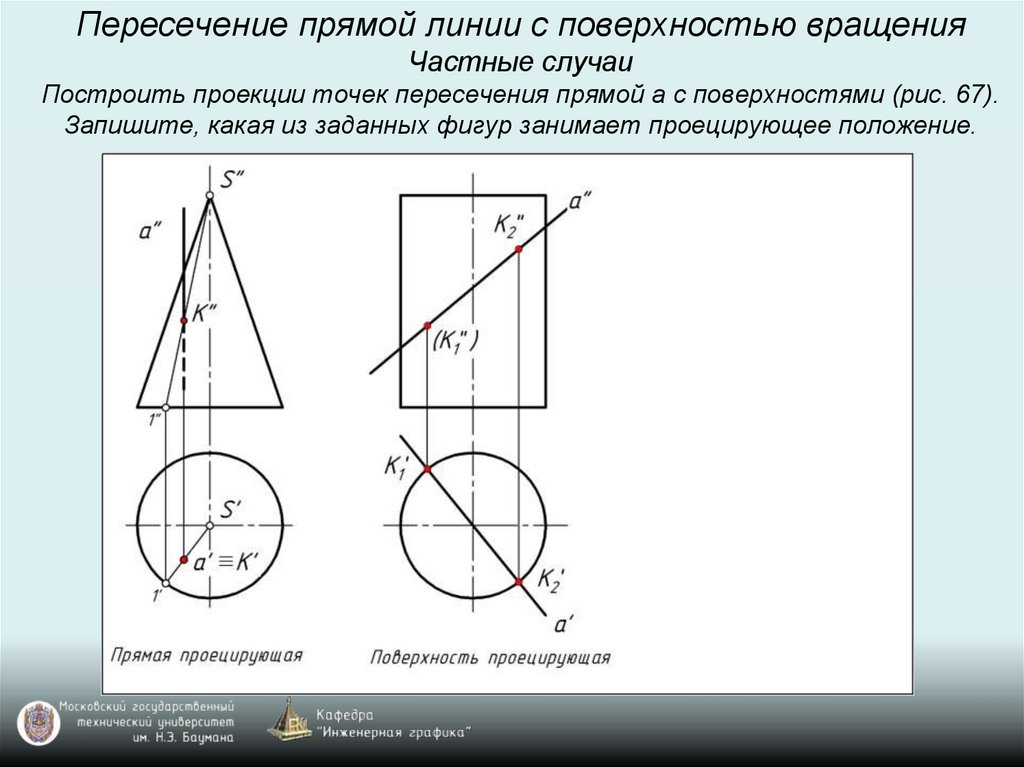
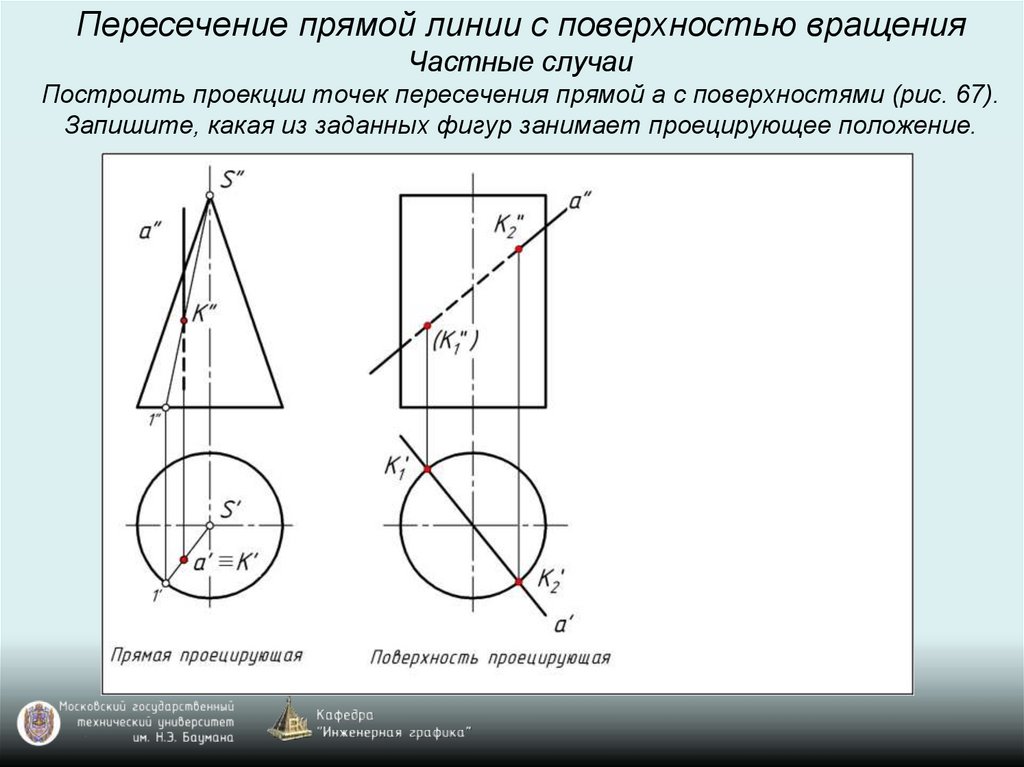
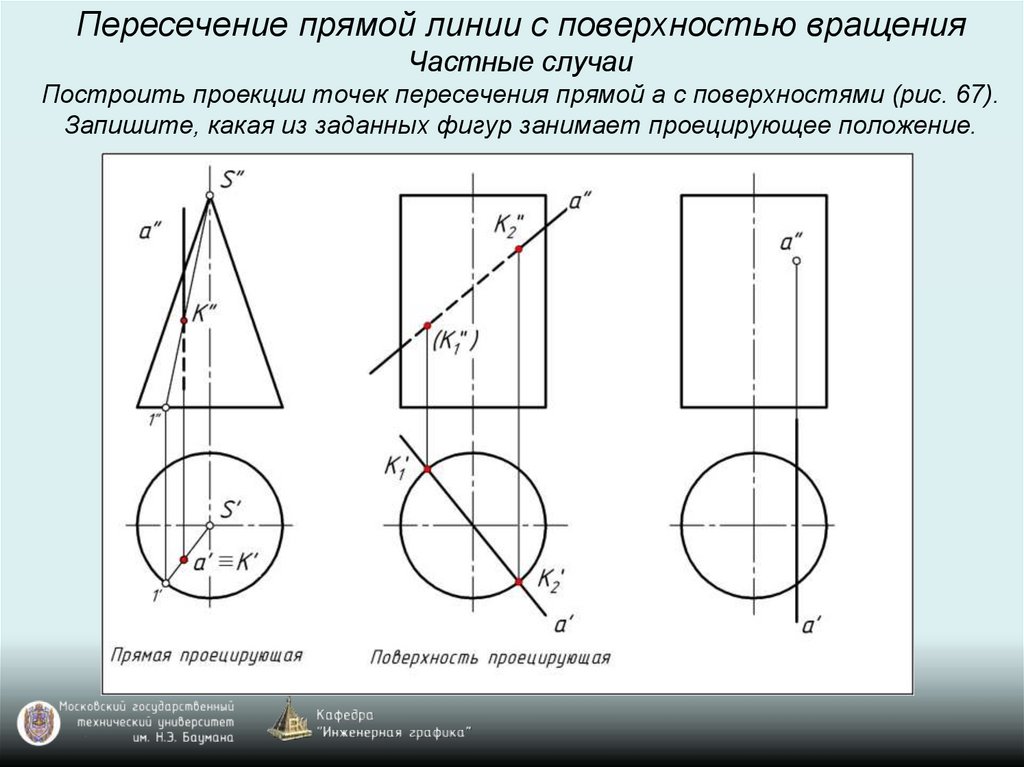
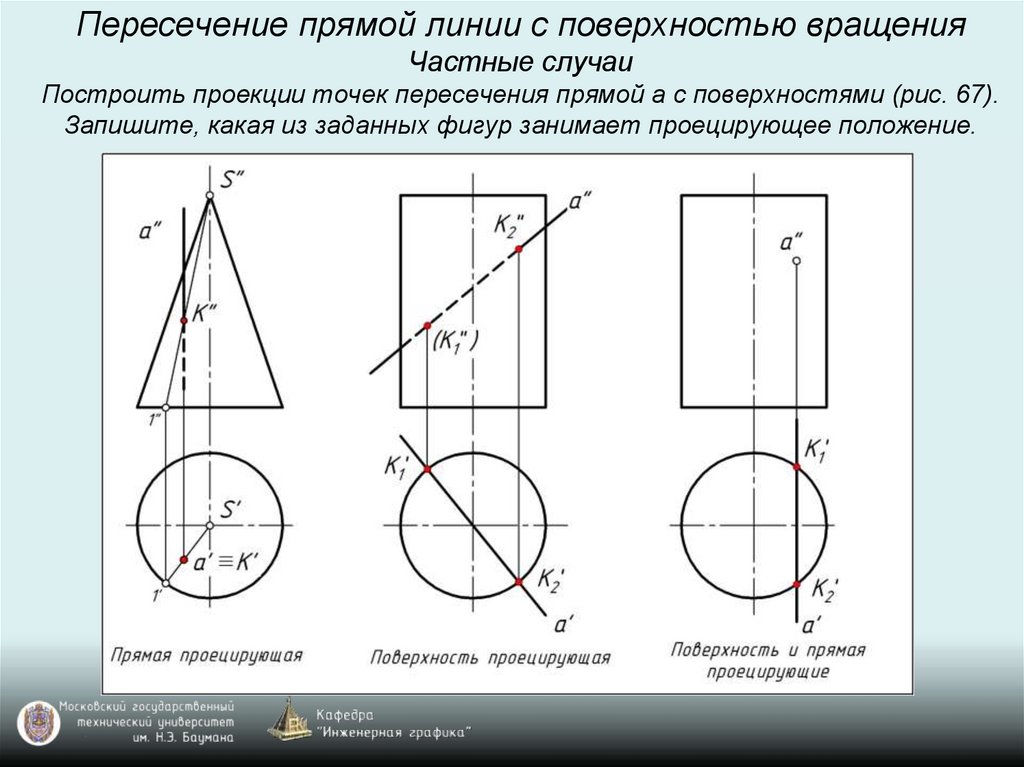
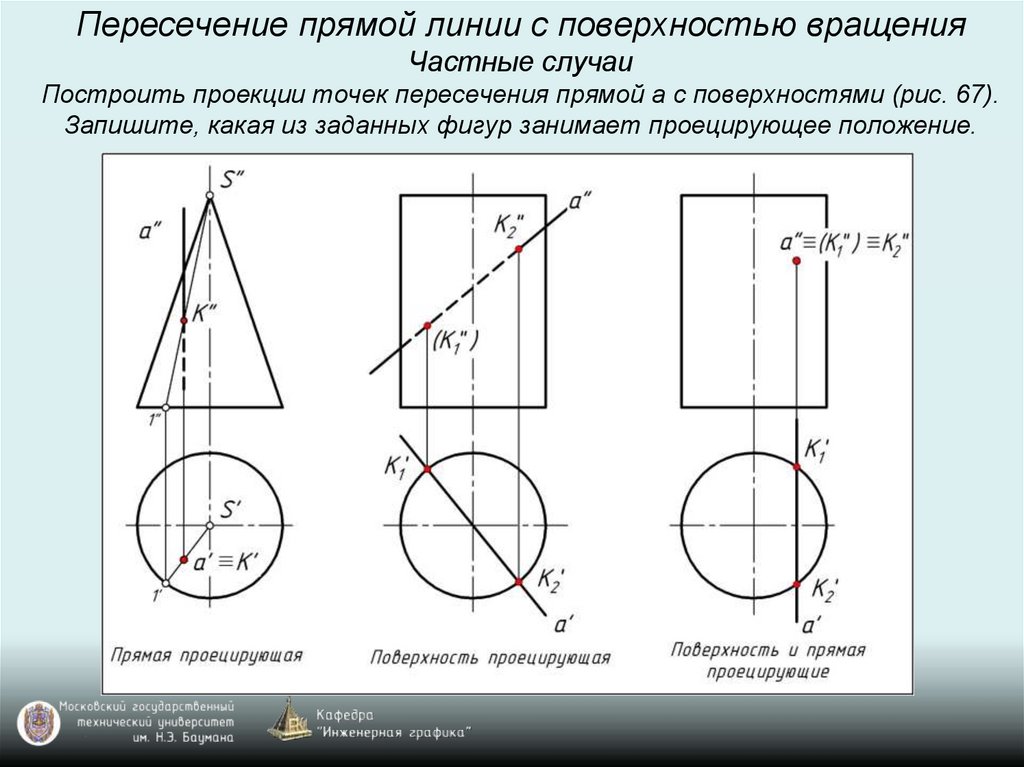
Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

72.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

73.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

74.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

75.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

76.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

77.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

78.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

79.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

80.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

81.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

82.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

83.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

84.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

85.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

86.

Пересечение прямой линии с поверхностью вращения
Частные случаи
Построить проекции точек пересечения прямой а с поверхностями (рис. 67).
Запишите, какая из заданных фигур занимает проецирующее положение.

87.

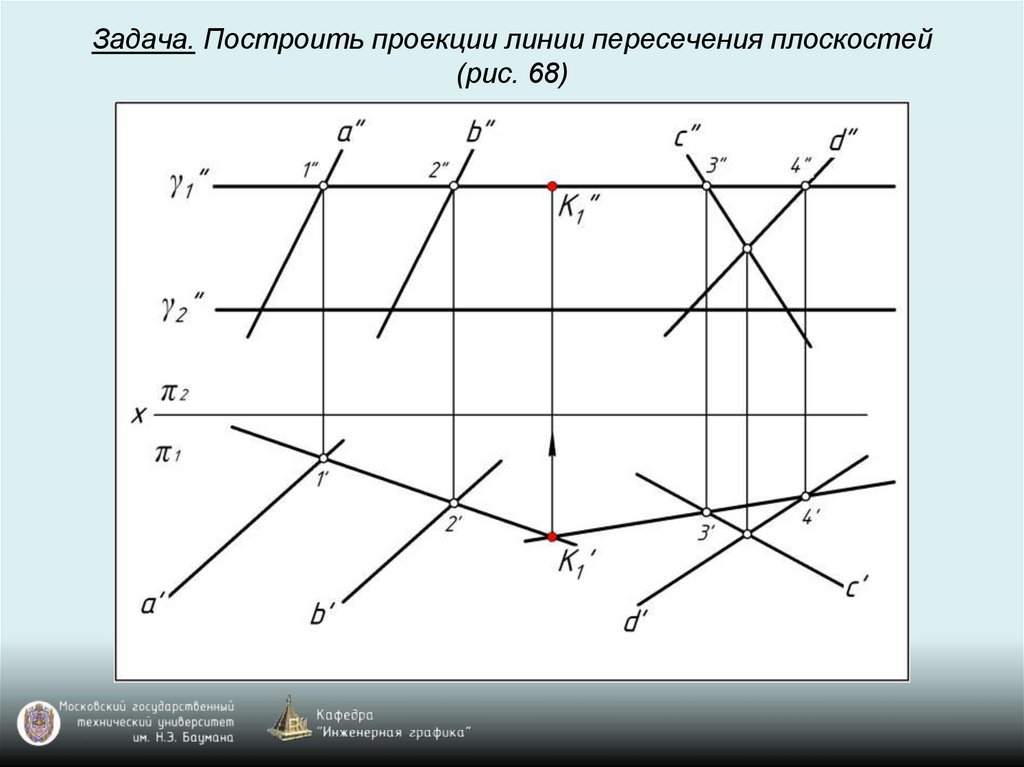
9.3.
Пересечение поверхностей
Общий случай
Последовательность построения линии пересечения
поверхностей:
α ∩ β → l1, l2 …
1) вводим γi – вспомогательные поверхности;
2) α ∩ γi → mi; β ∩ γ i → ni;
3) mi ∩ ni (т.к. лежат в одной поверхности γi), mi ∩ ni → Ki
4) K1 U K2 U K3 … U Ki → l

88.

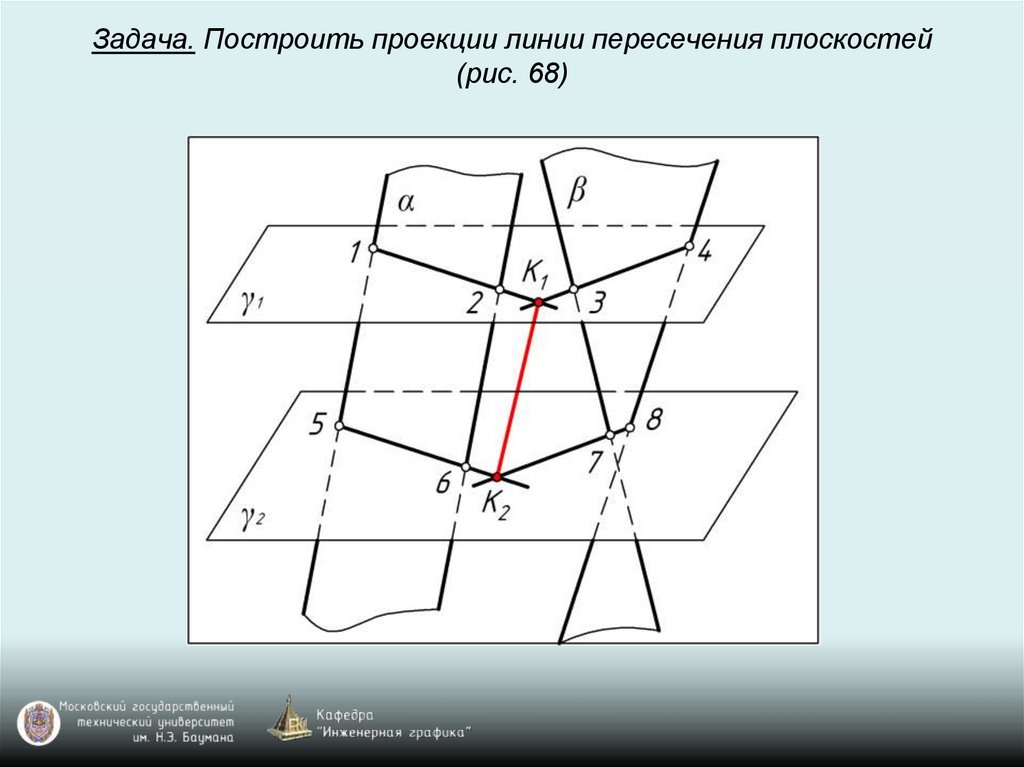
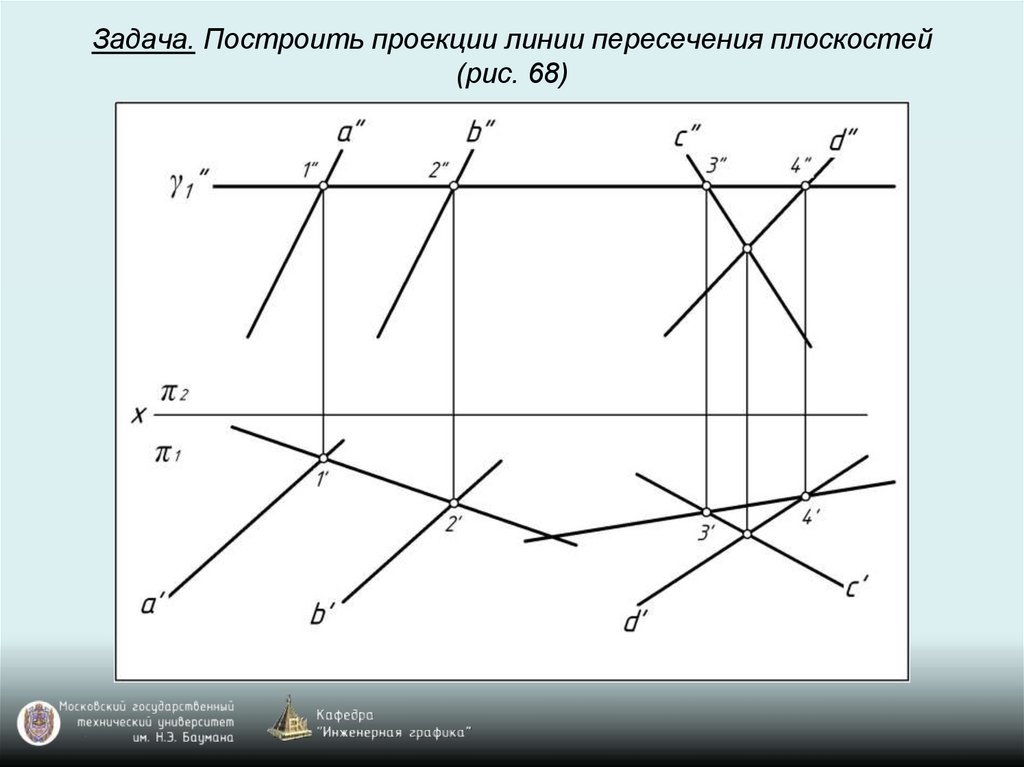
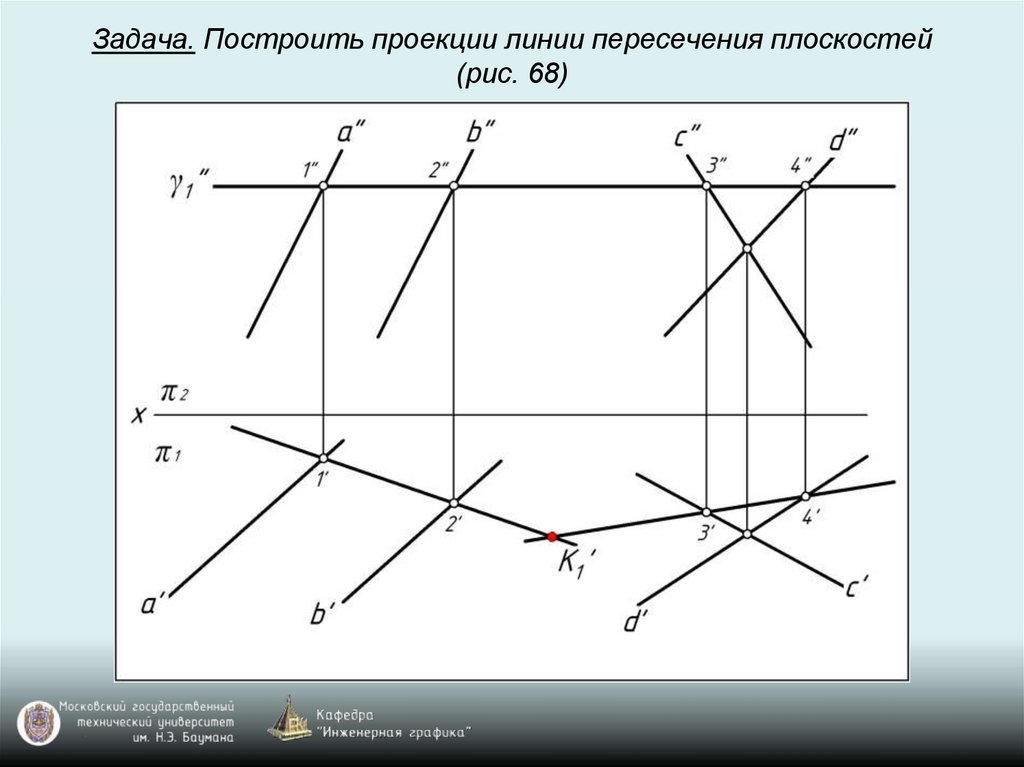
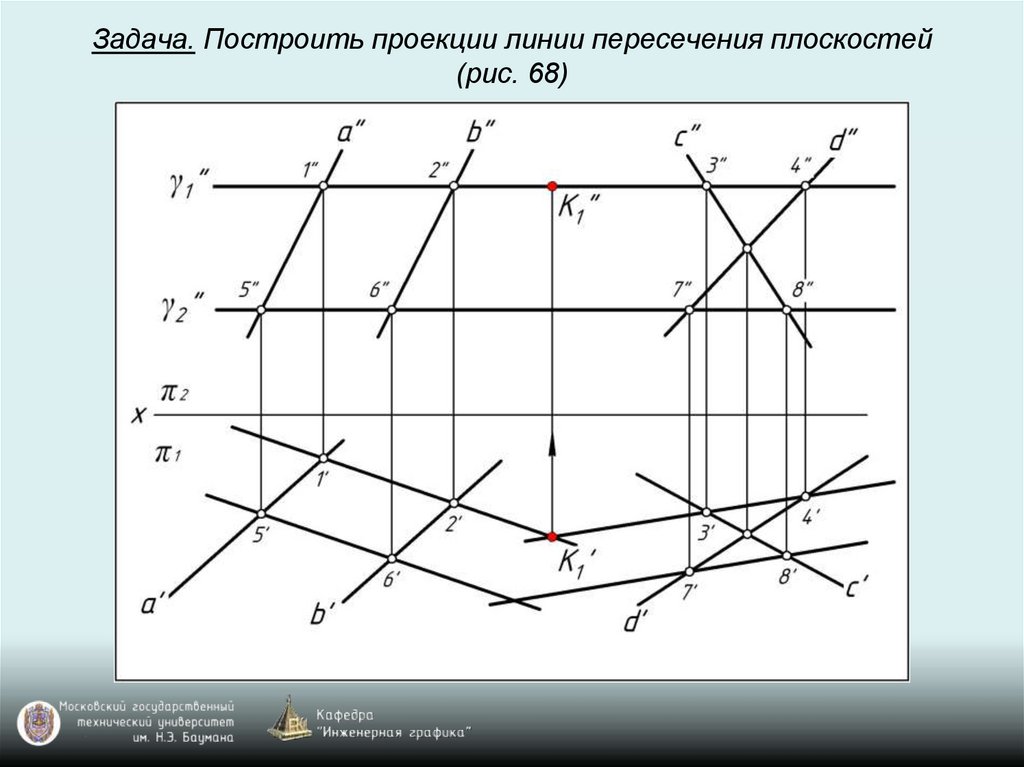
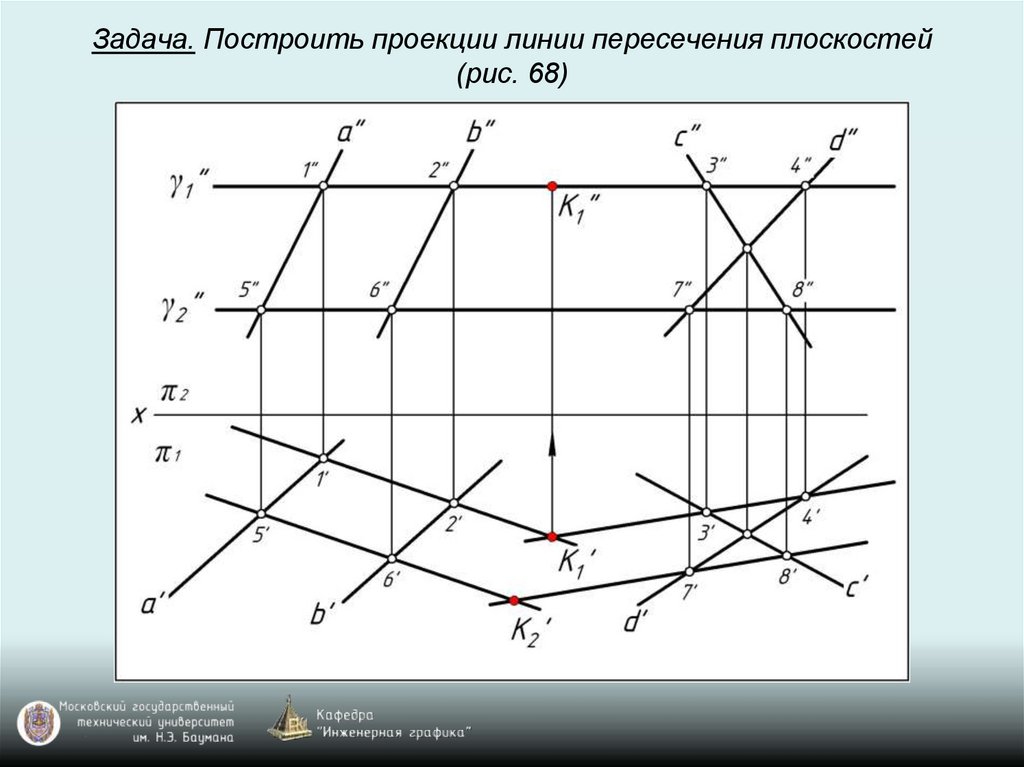
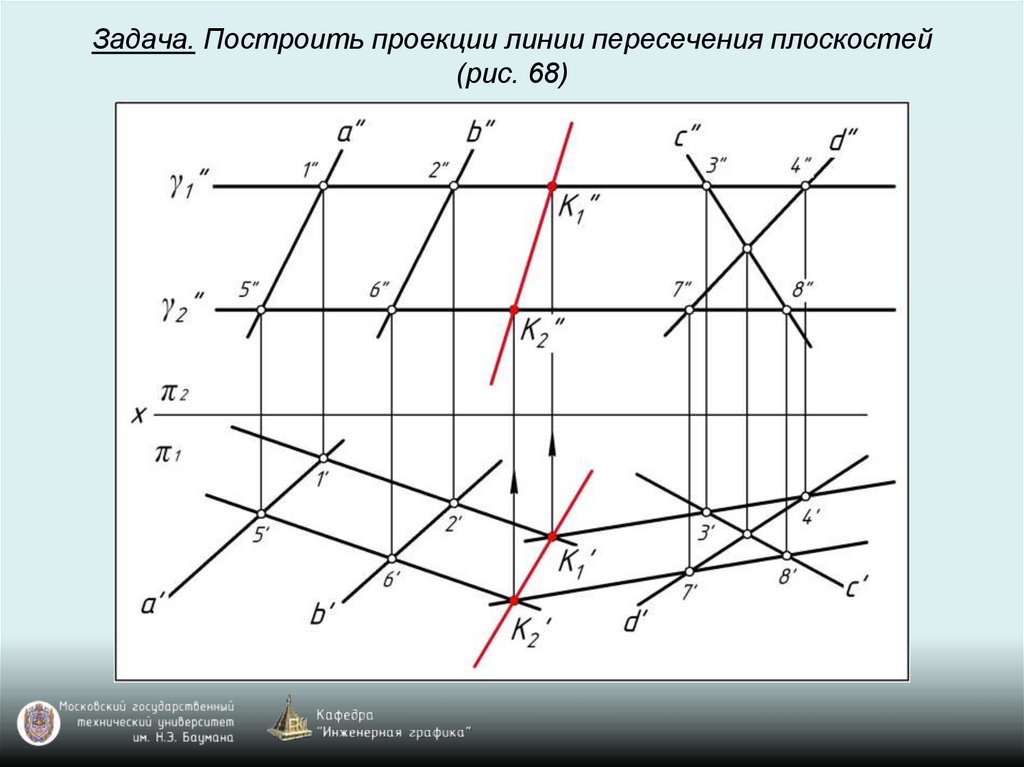
Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

89.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

90.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

91.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

92.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

93.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

94.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

95.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

96.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

97.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

98.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

99.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

100.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

101.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

102.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

103.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

104.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

105.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

106.

Задача. Построить проекции линии пересечения плоскостей
(рис. 68)

107.

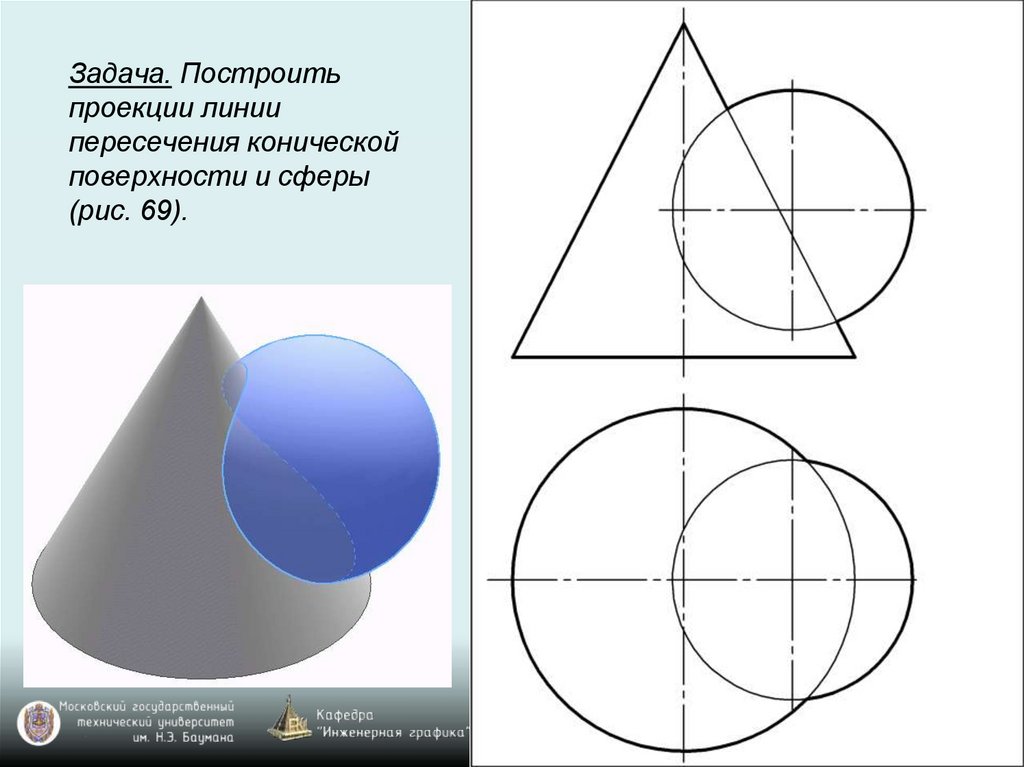
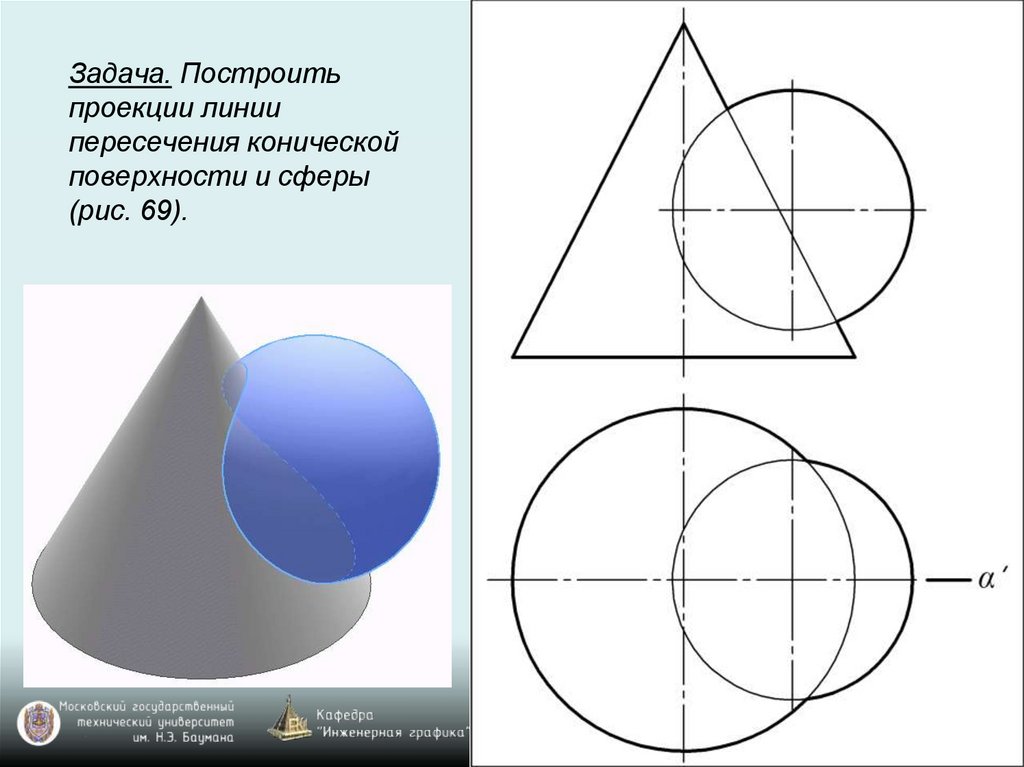
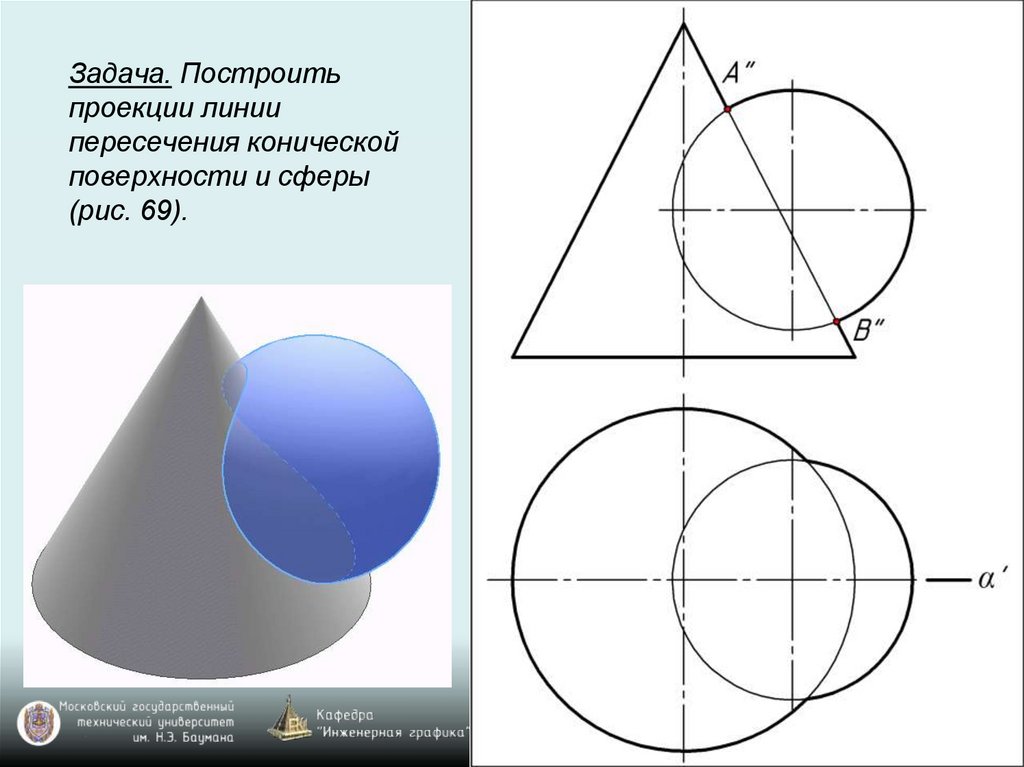
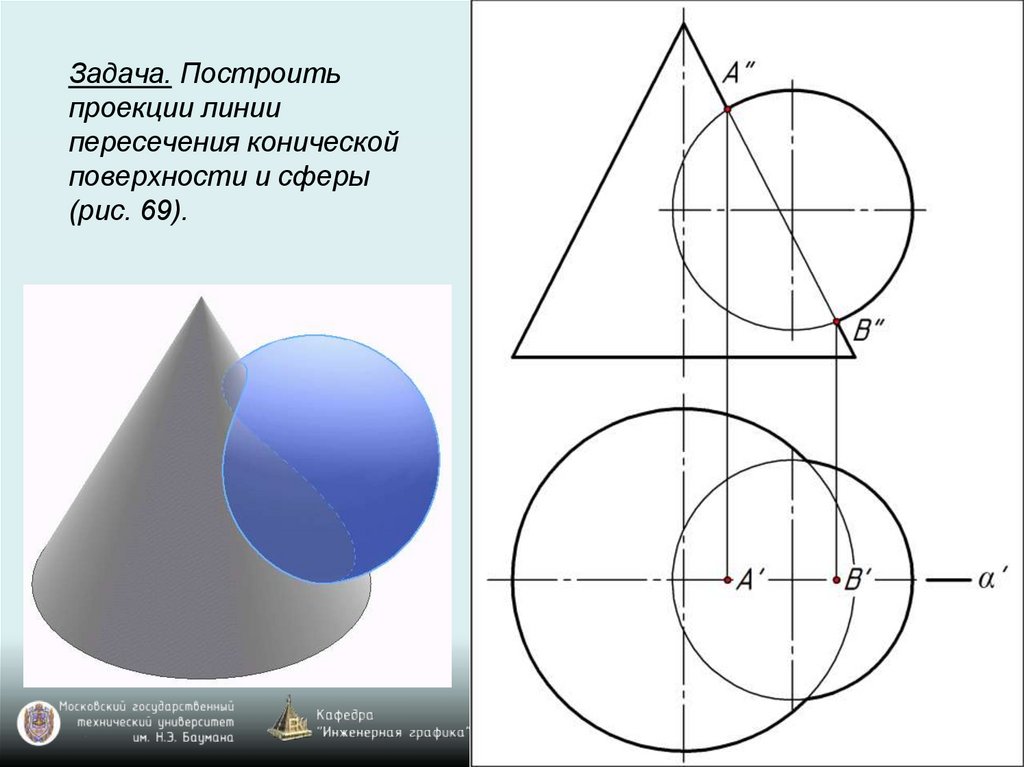
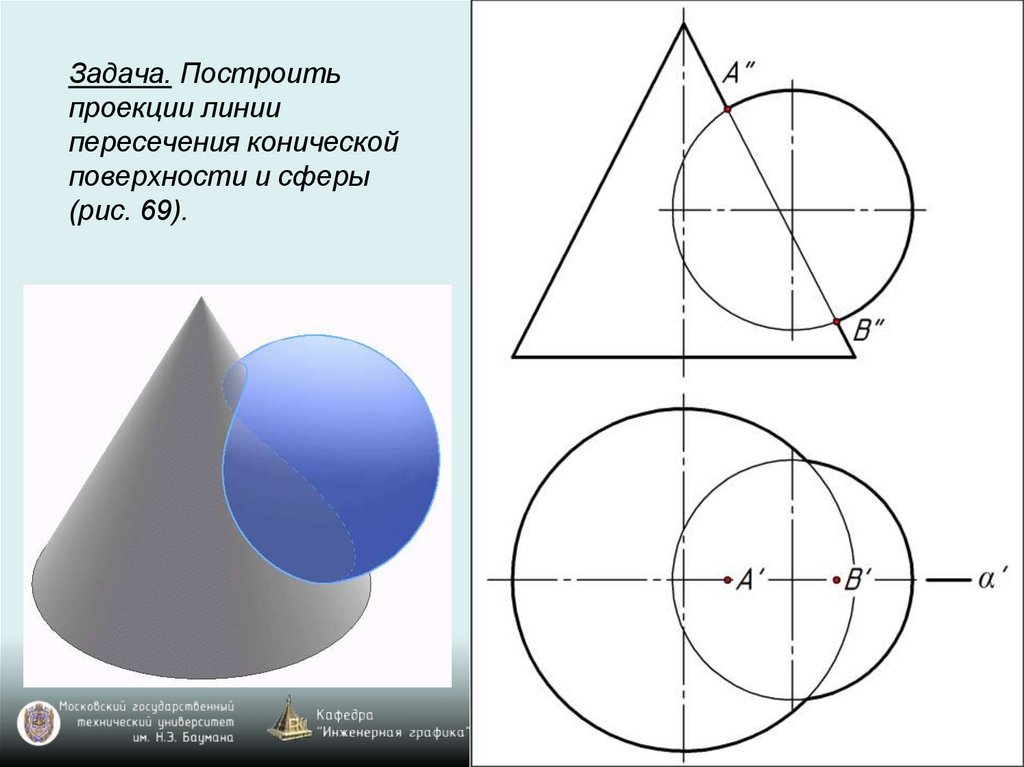
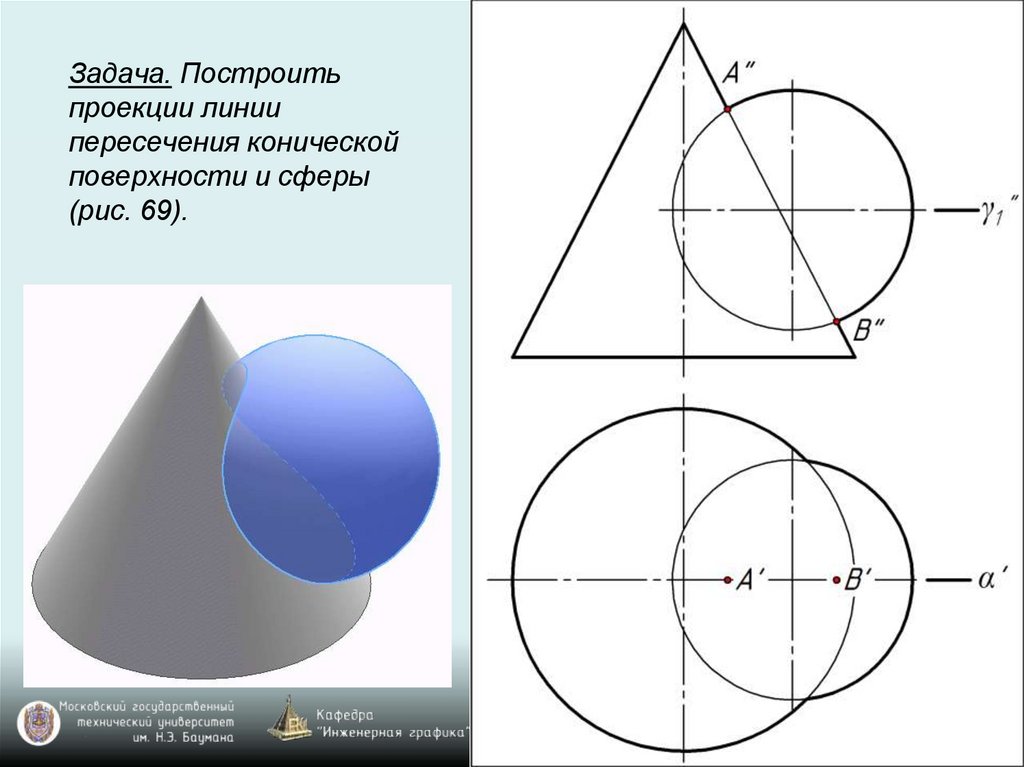
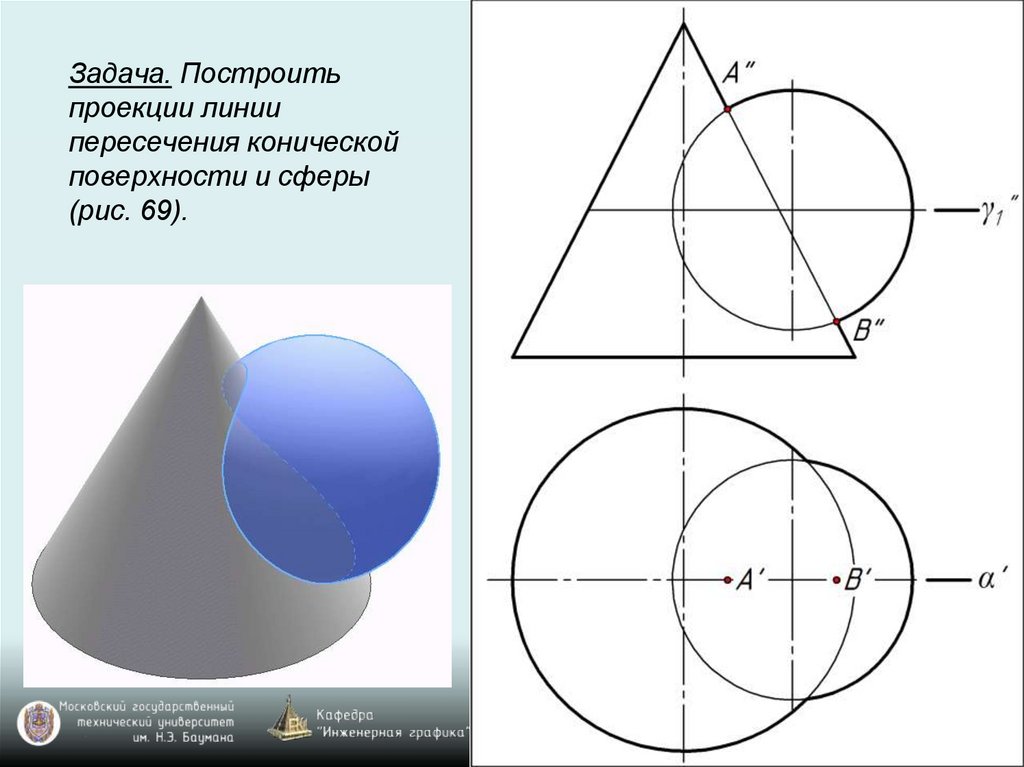
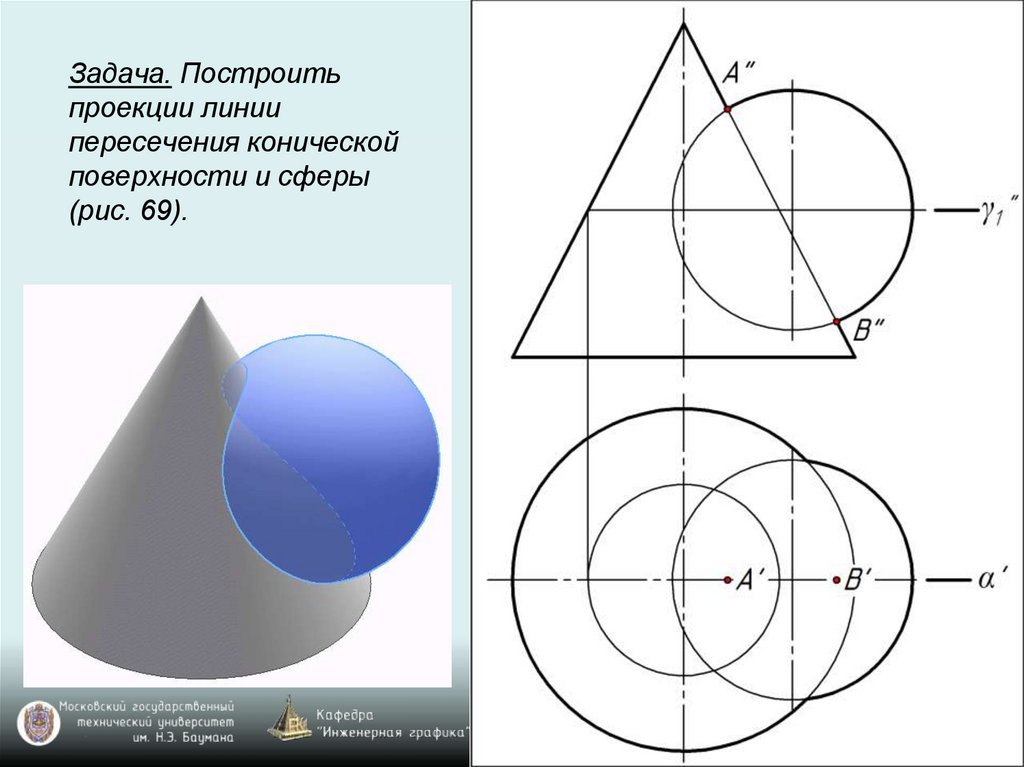
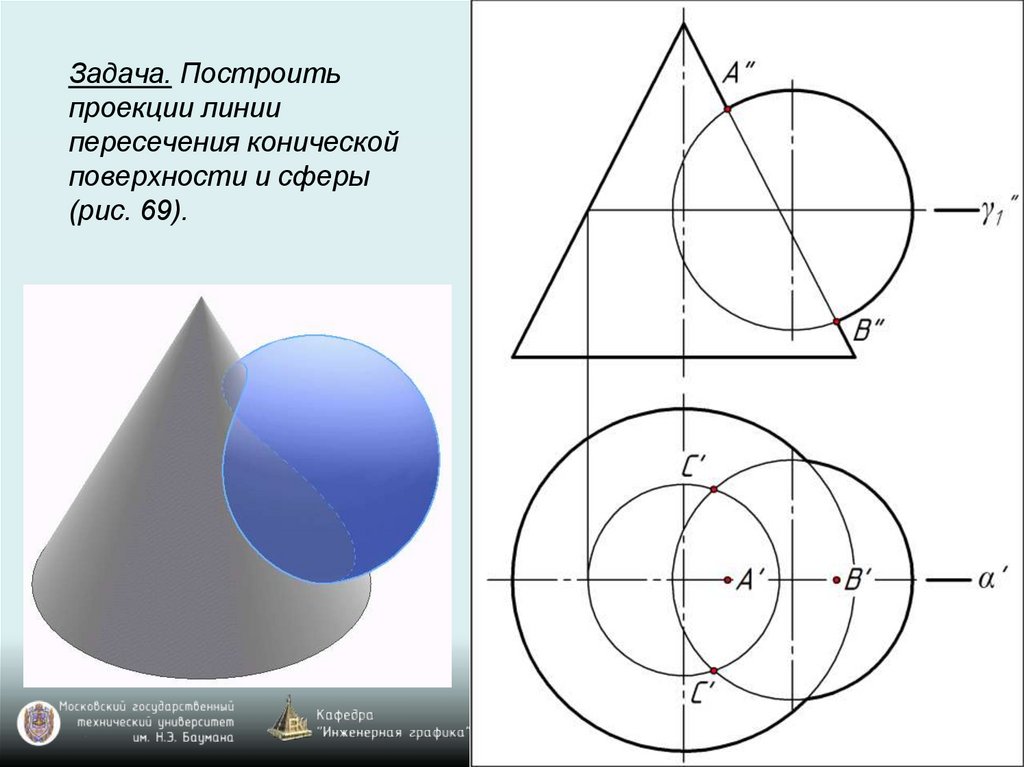
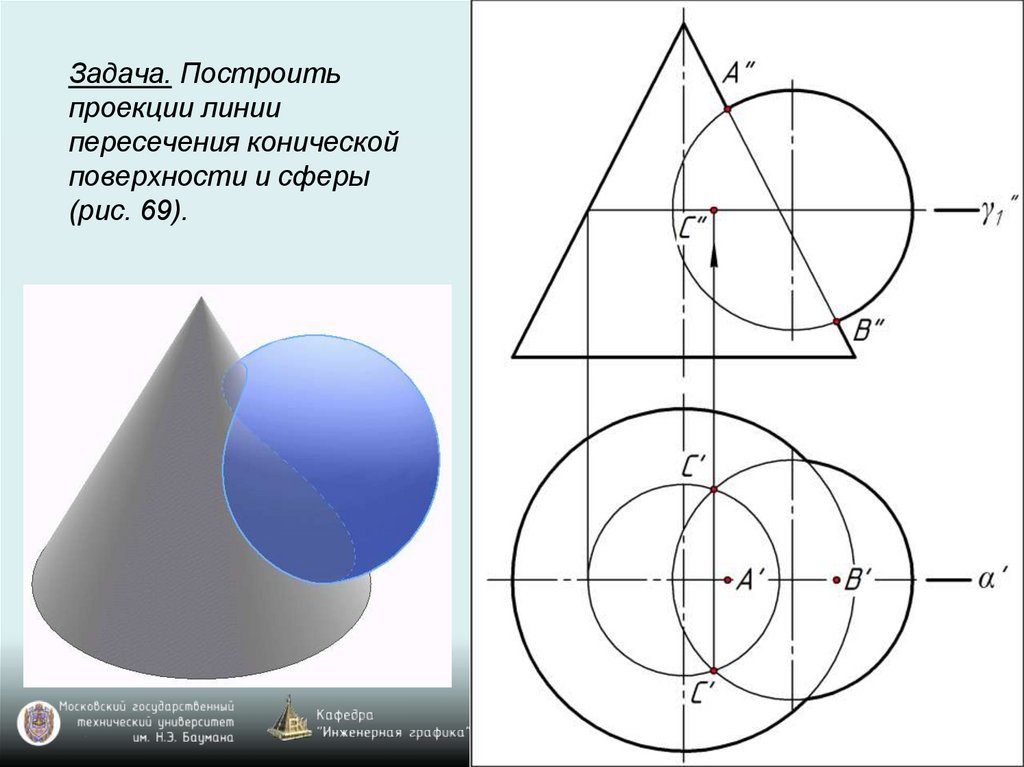
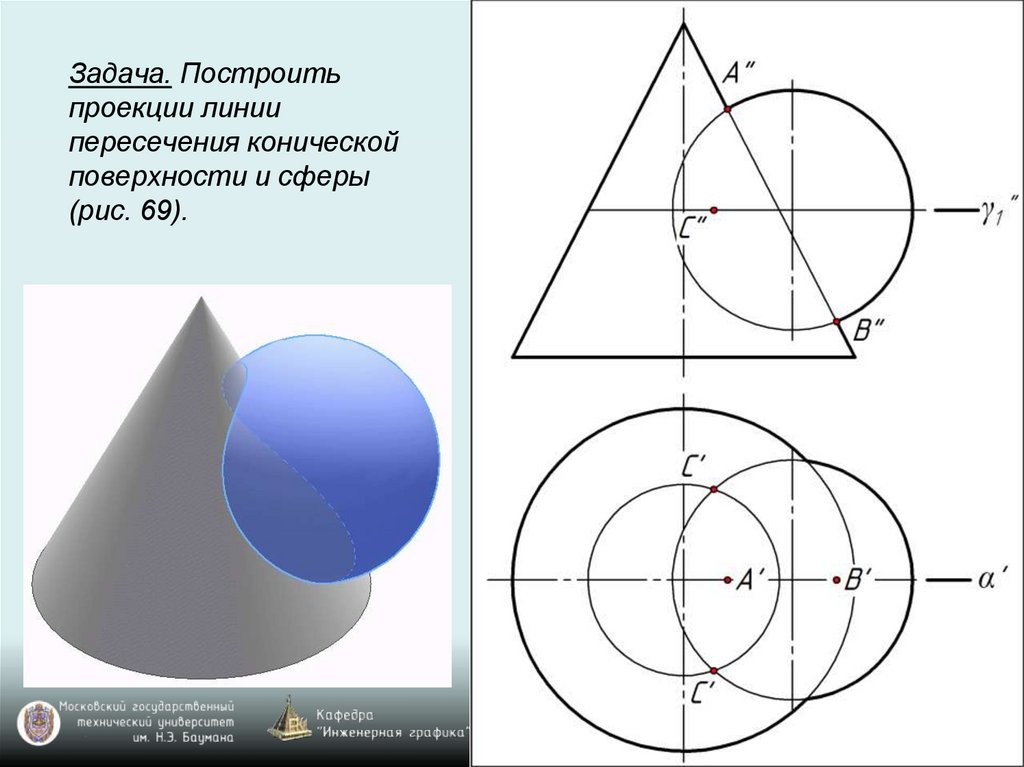
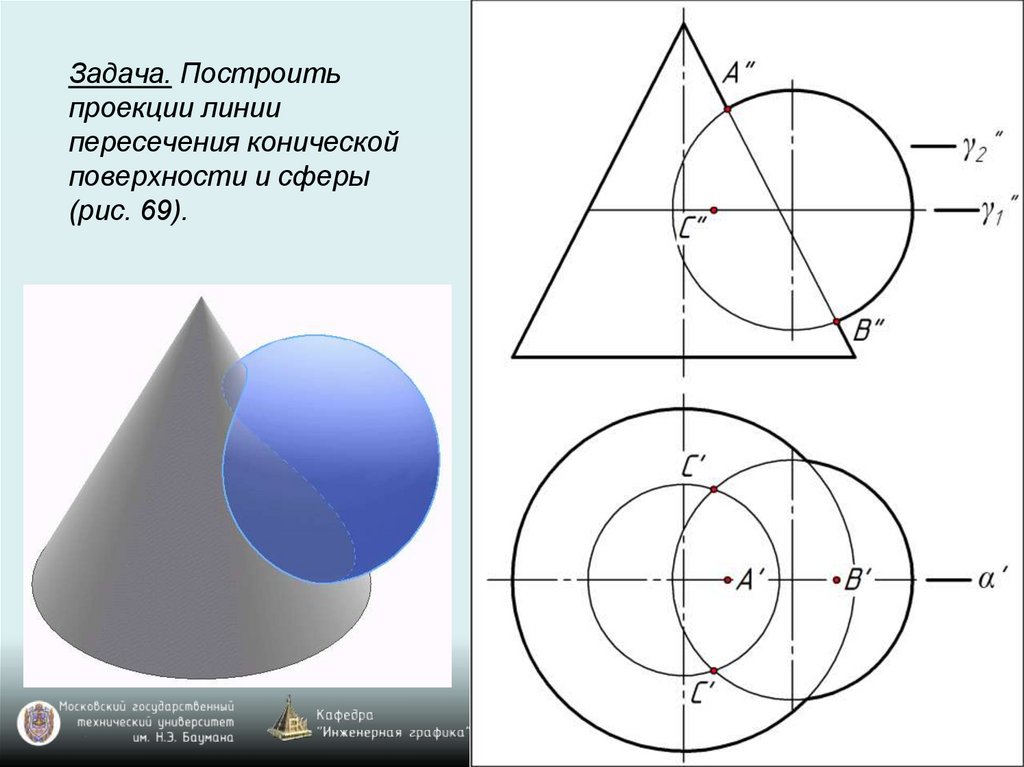
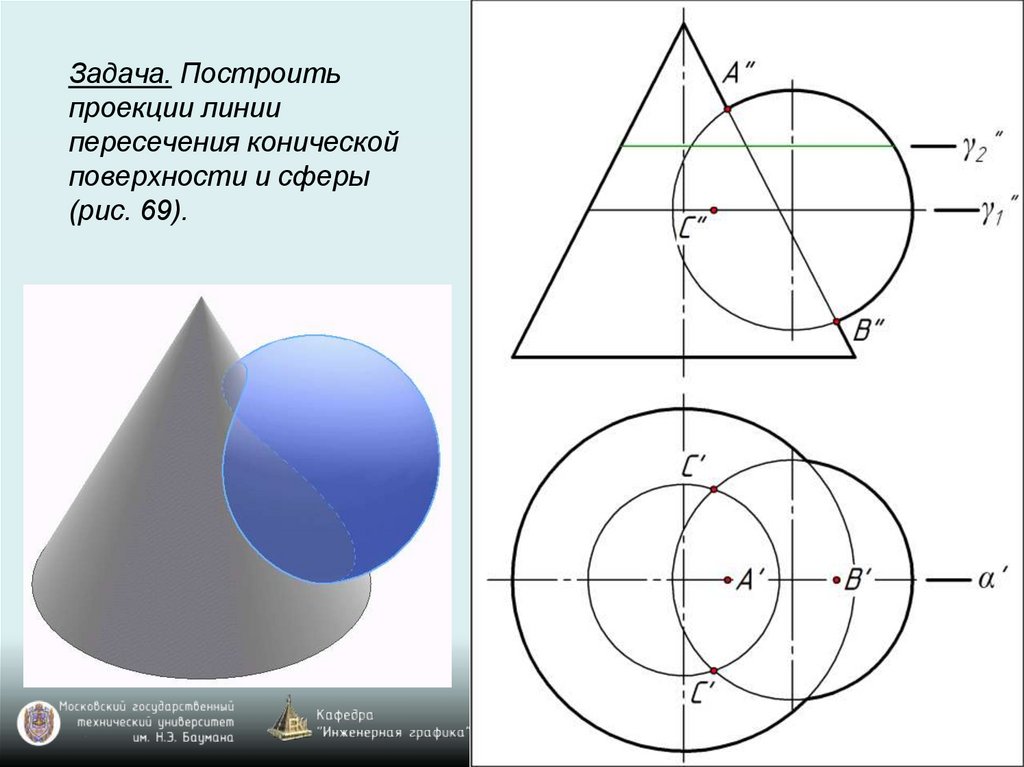
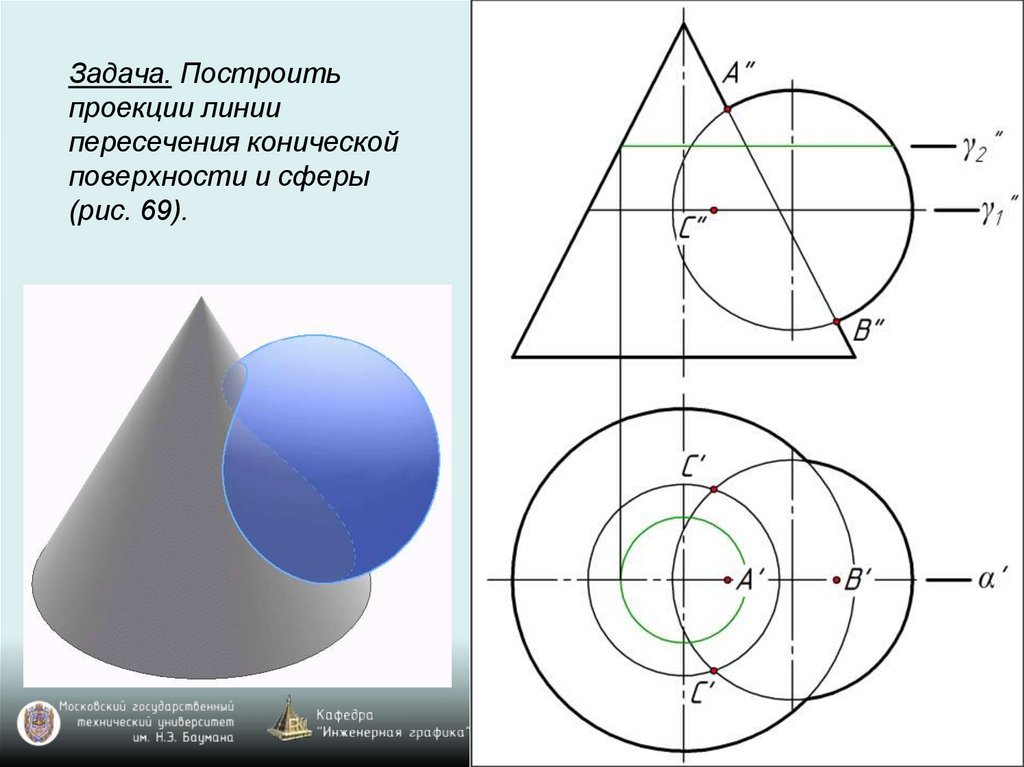
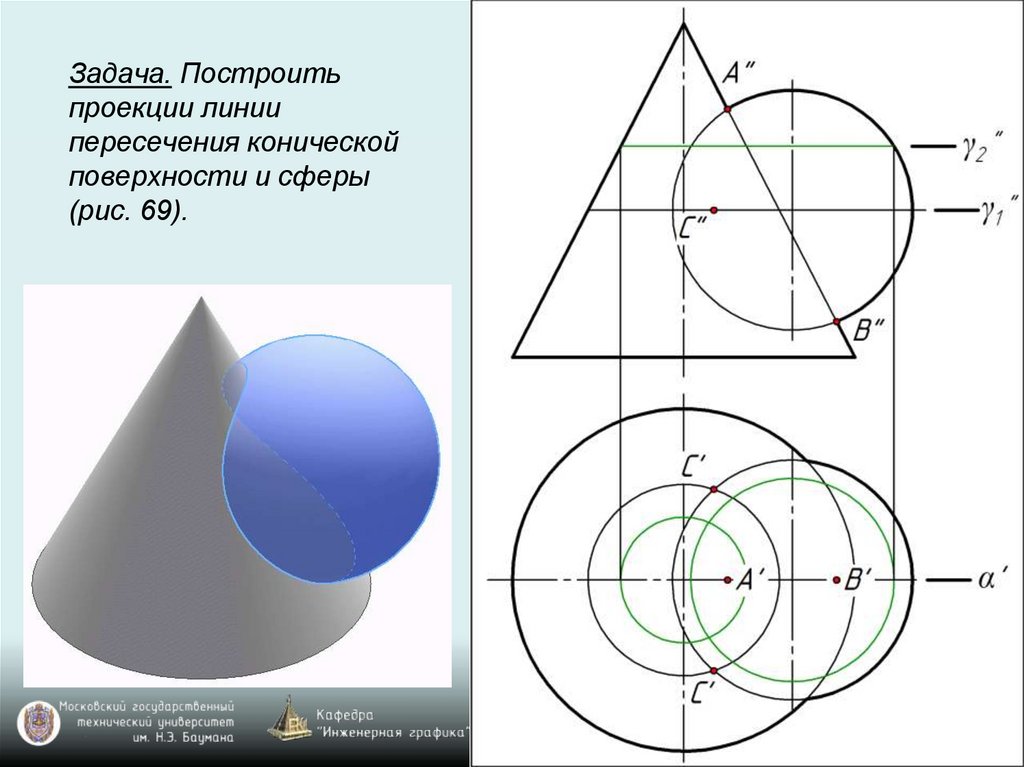
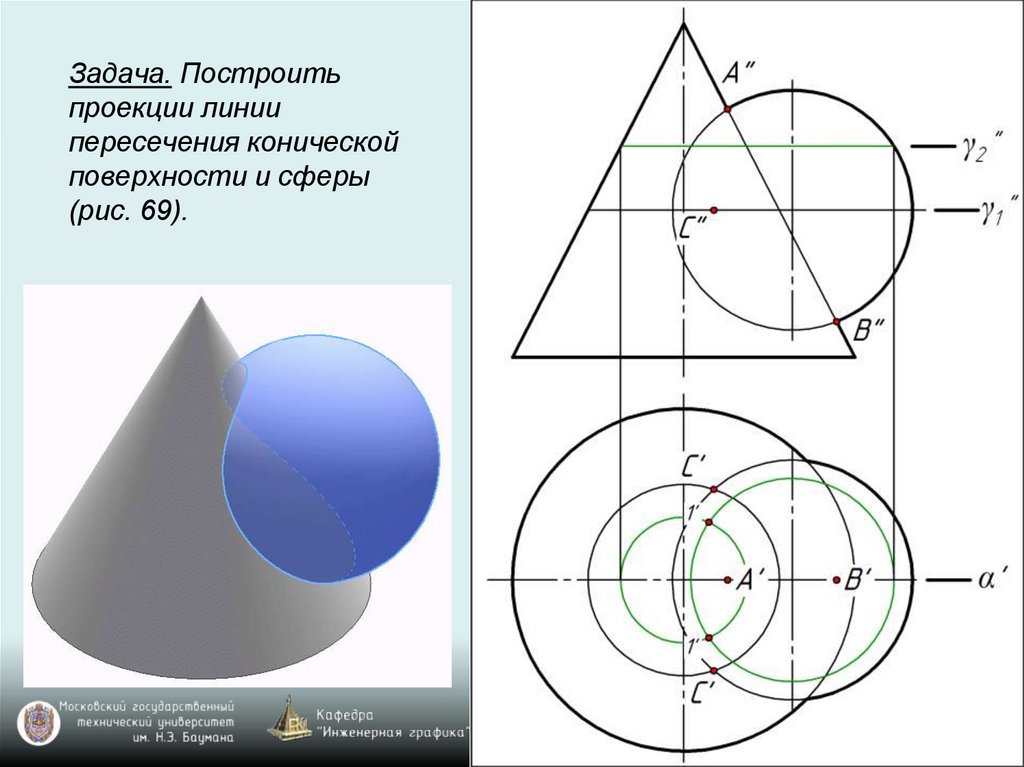
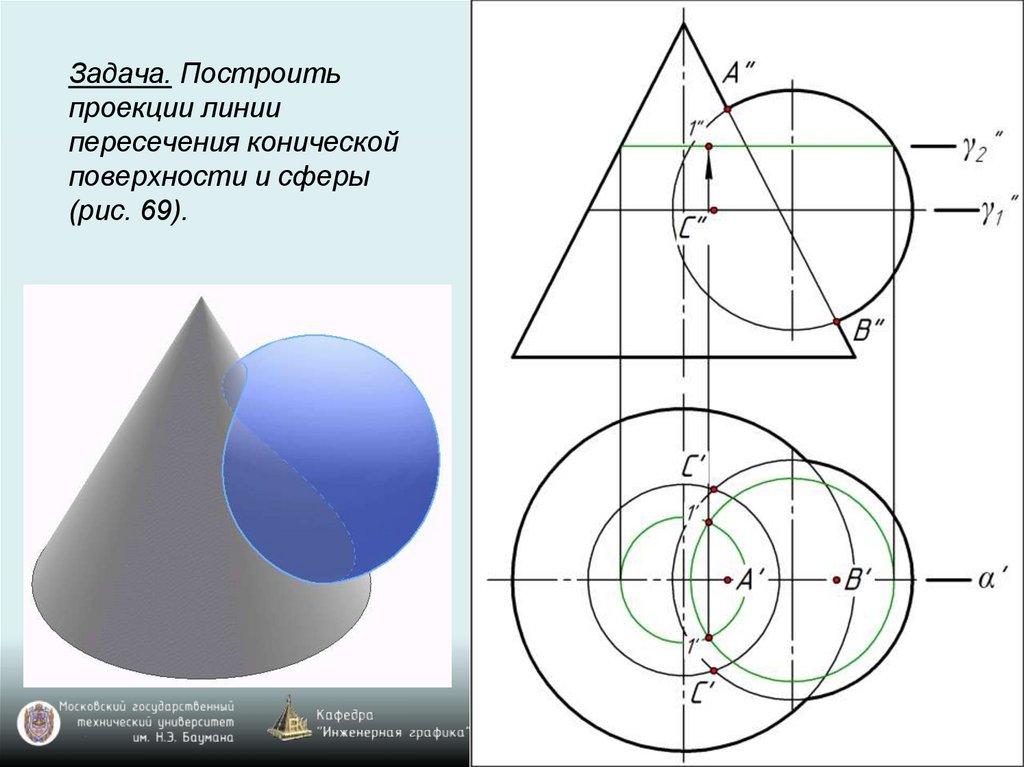
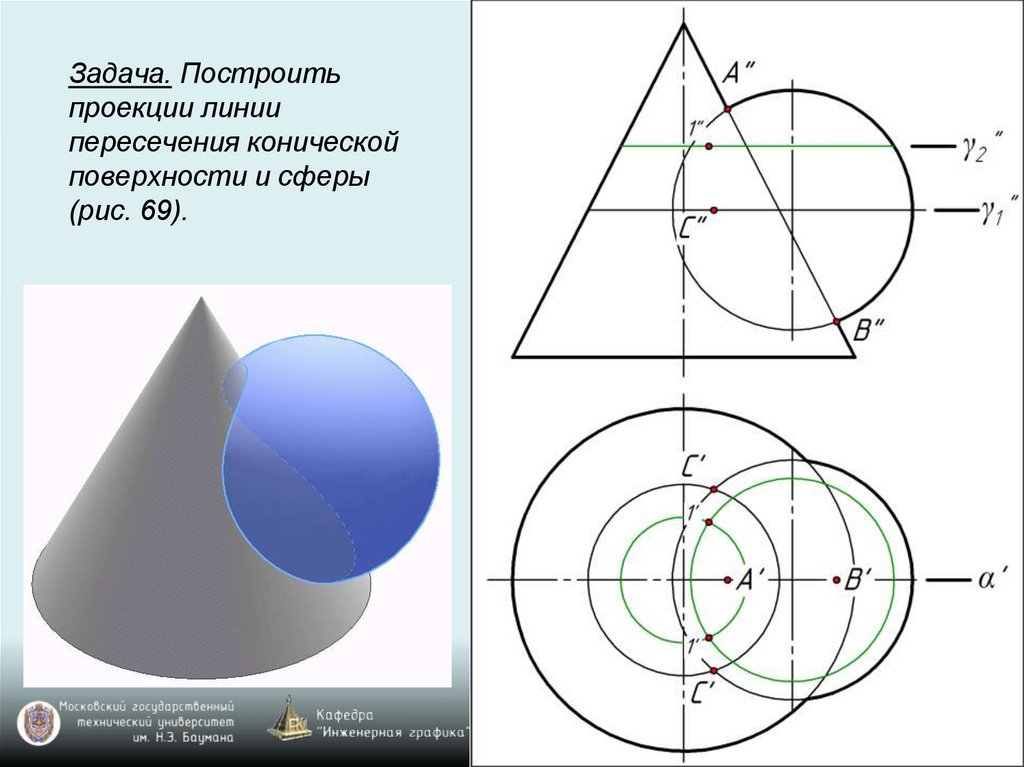
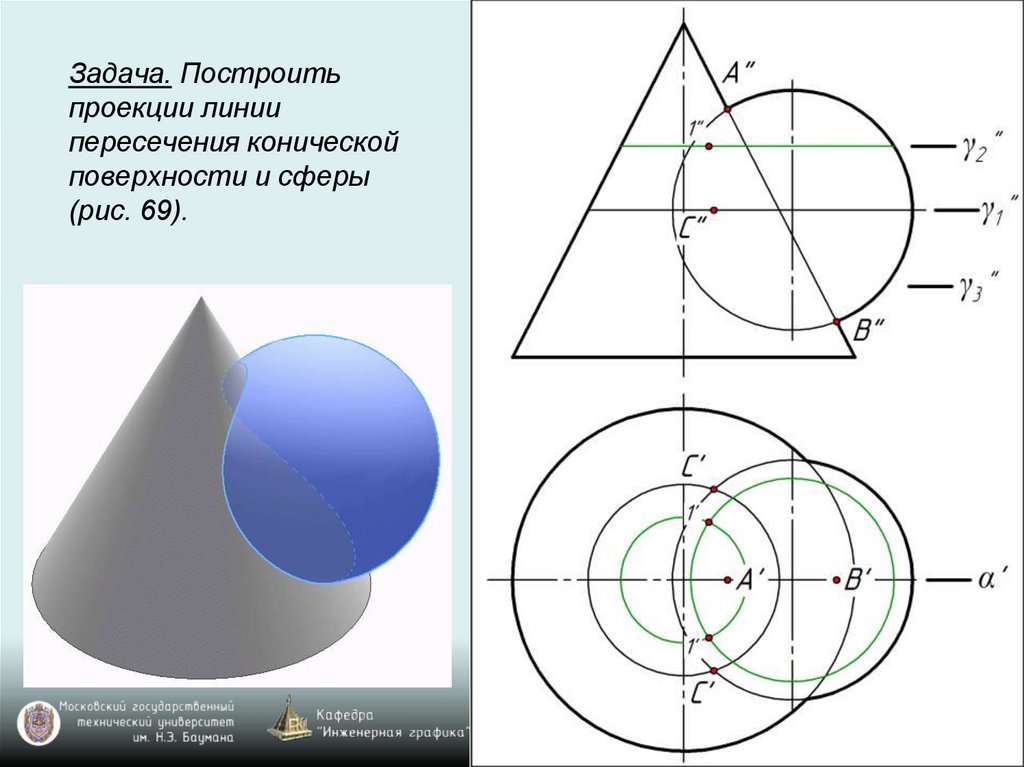
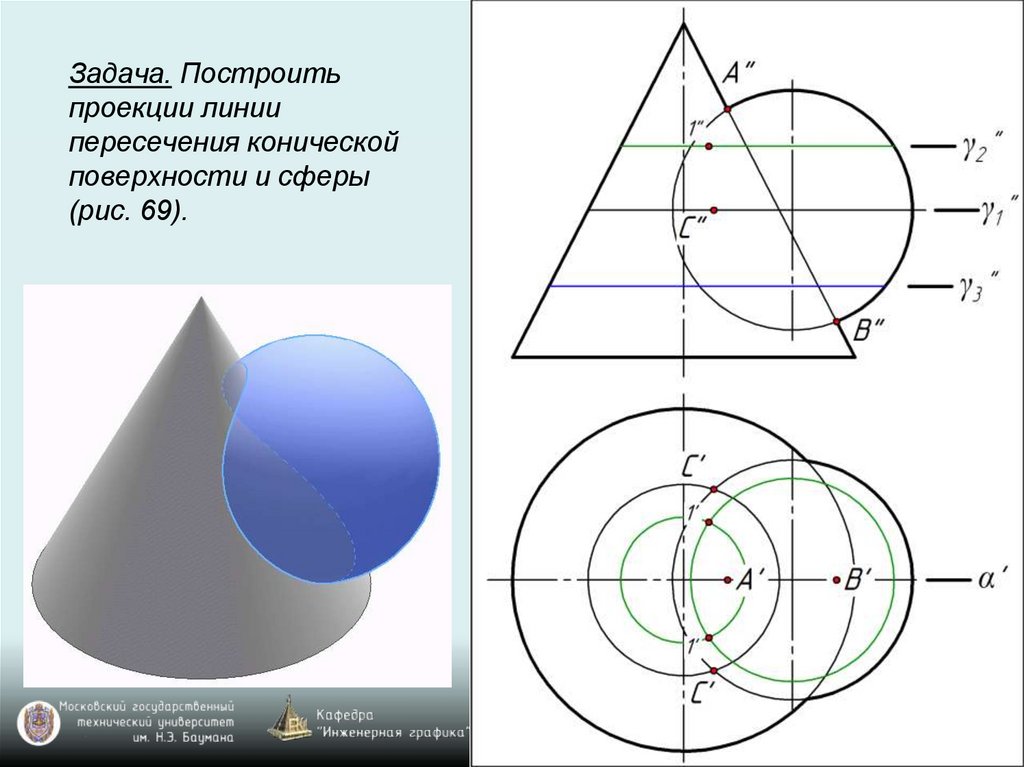
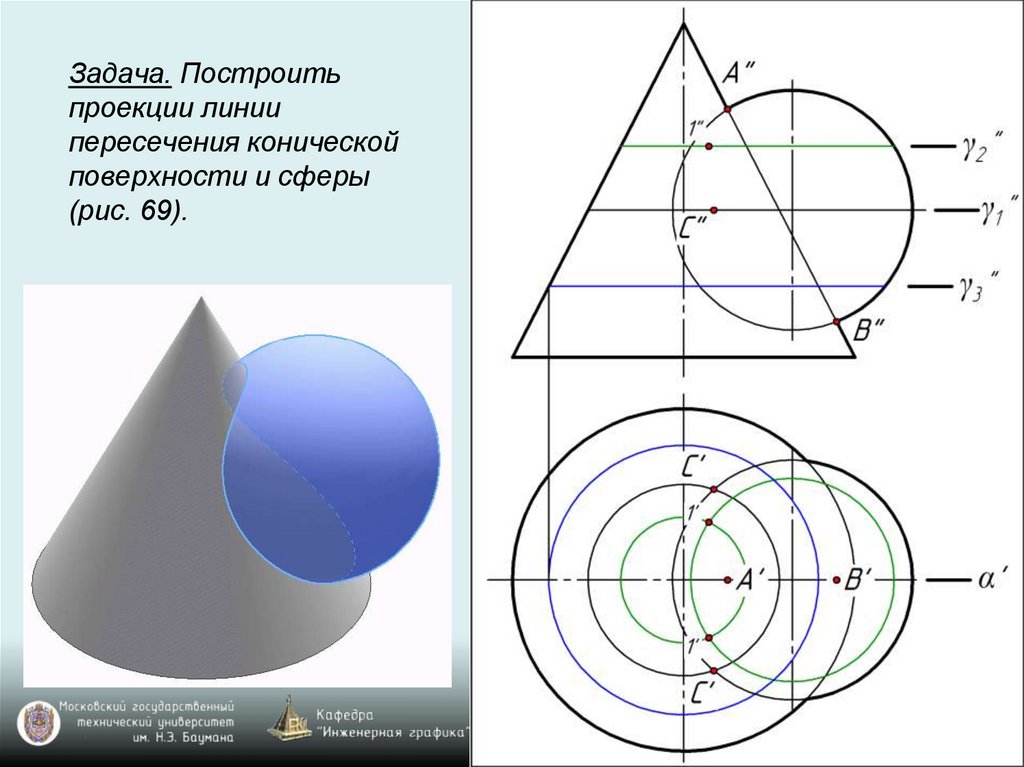
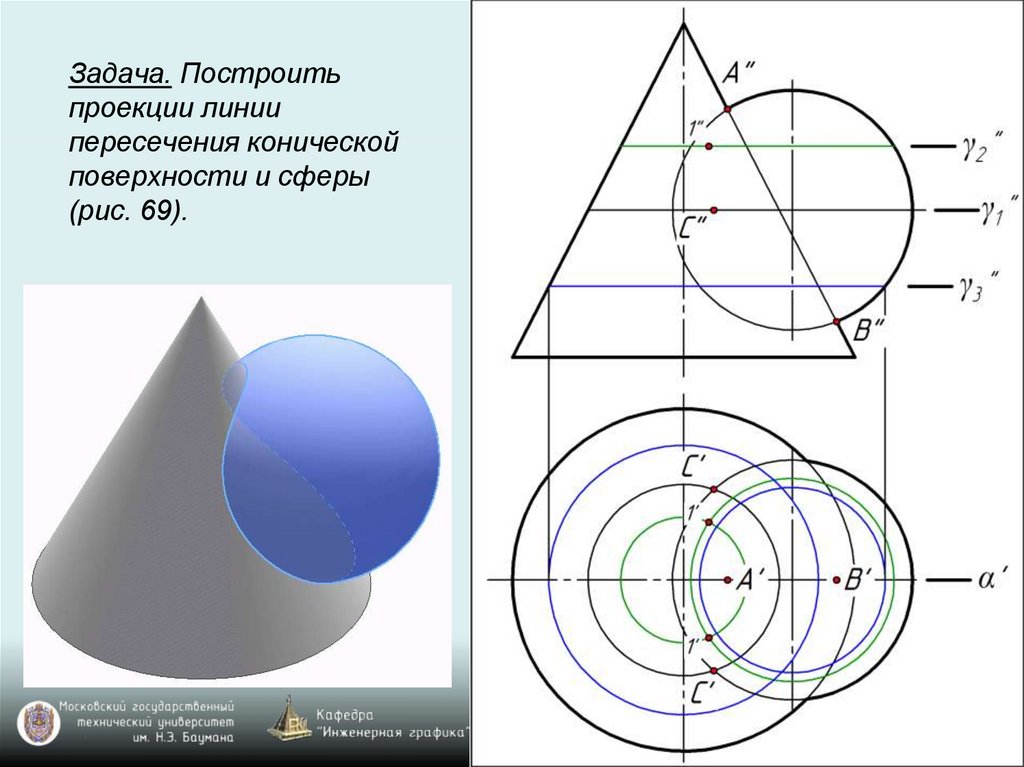
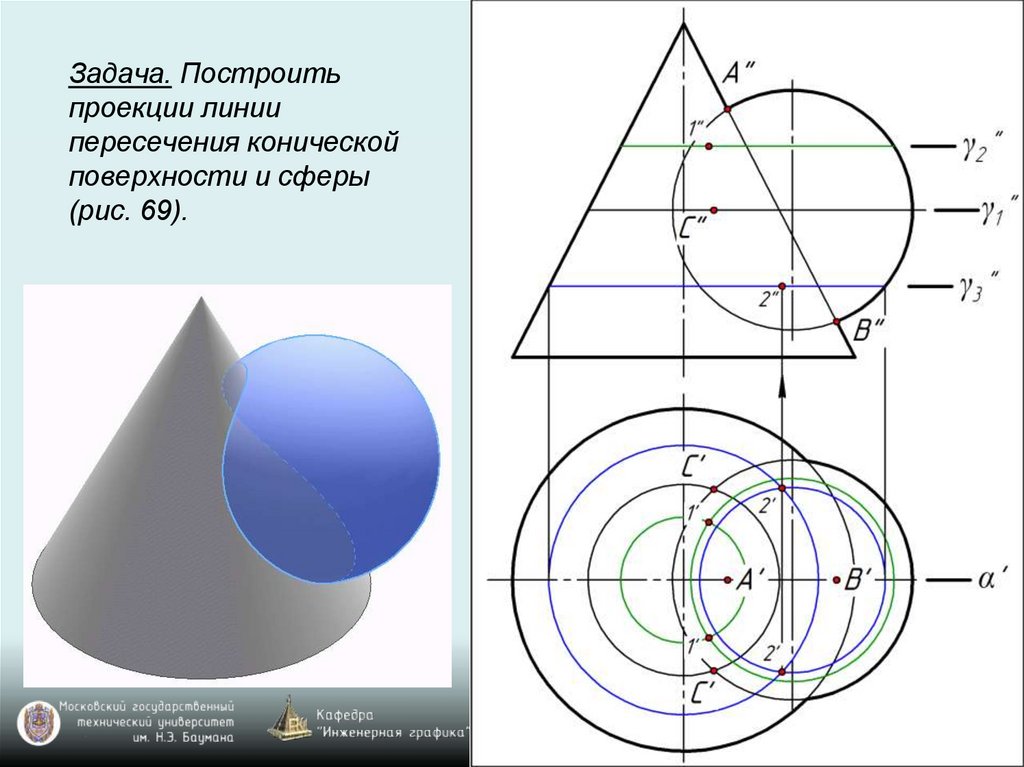
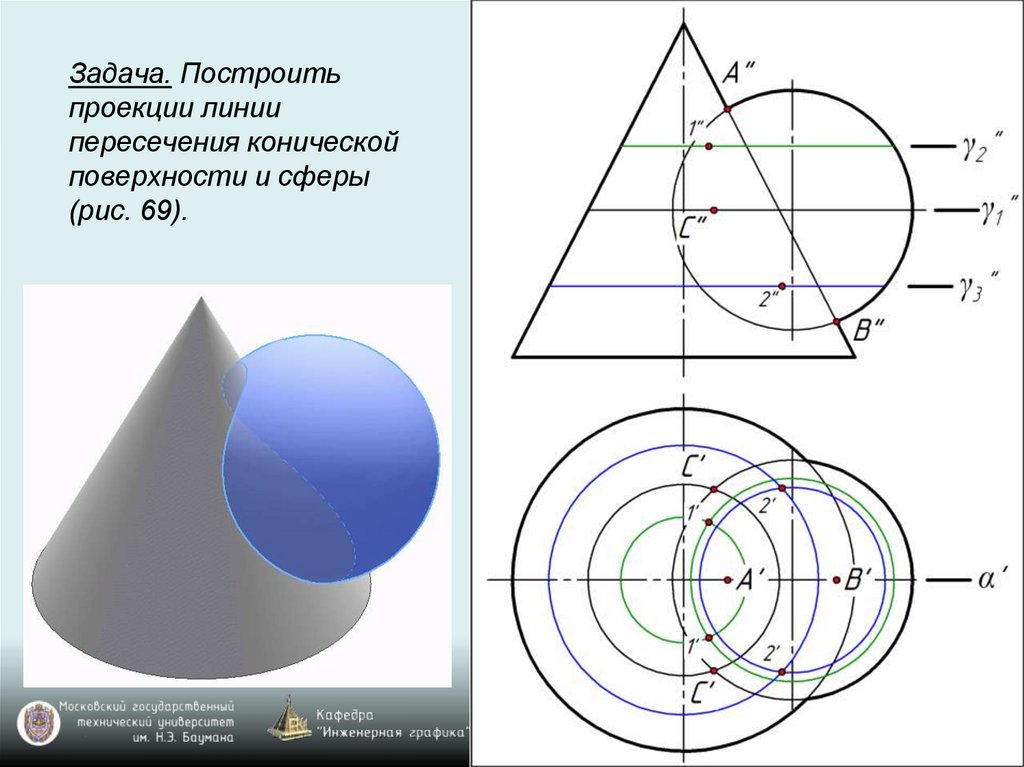
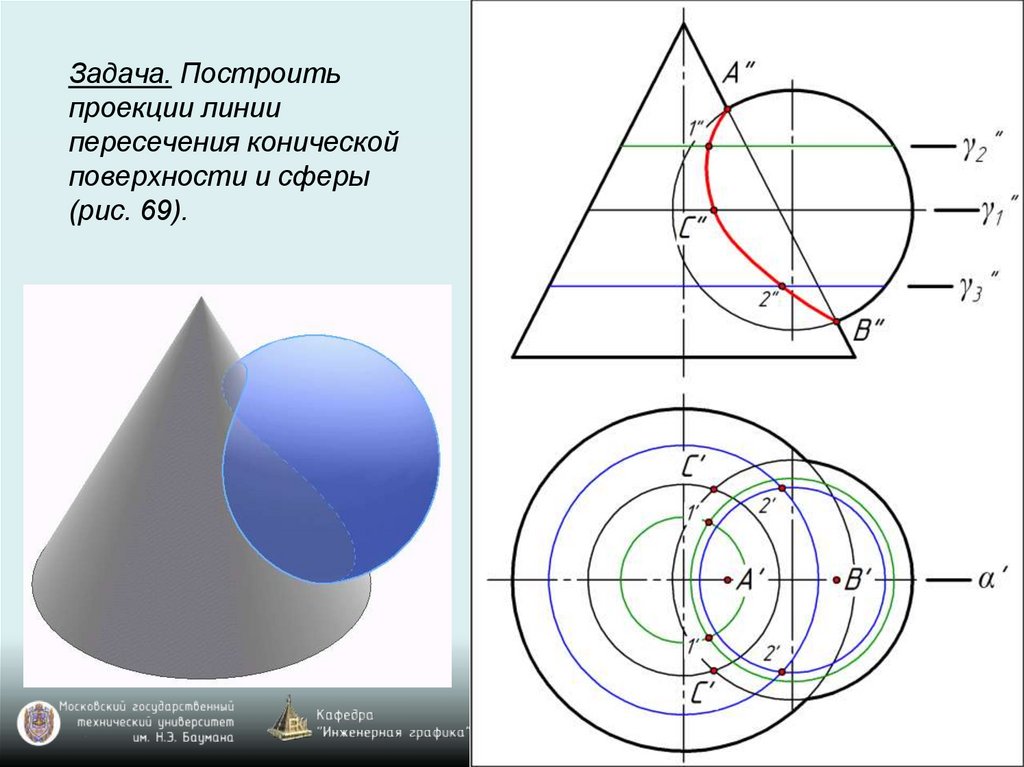
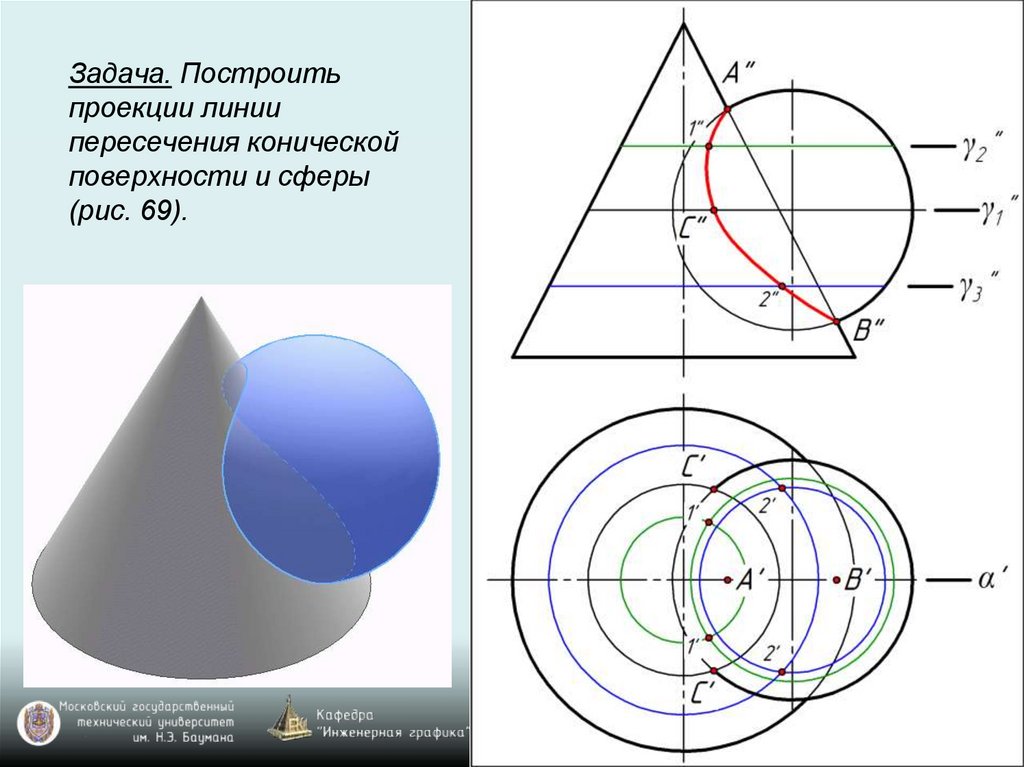
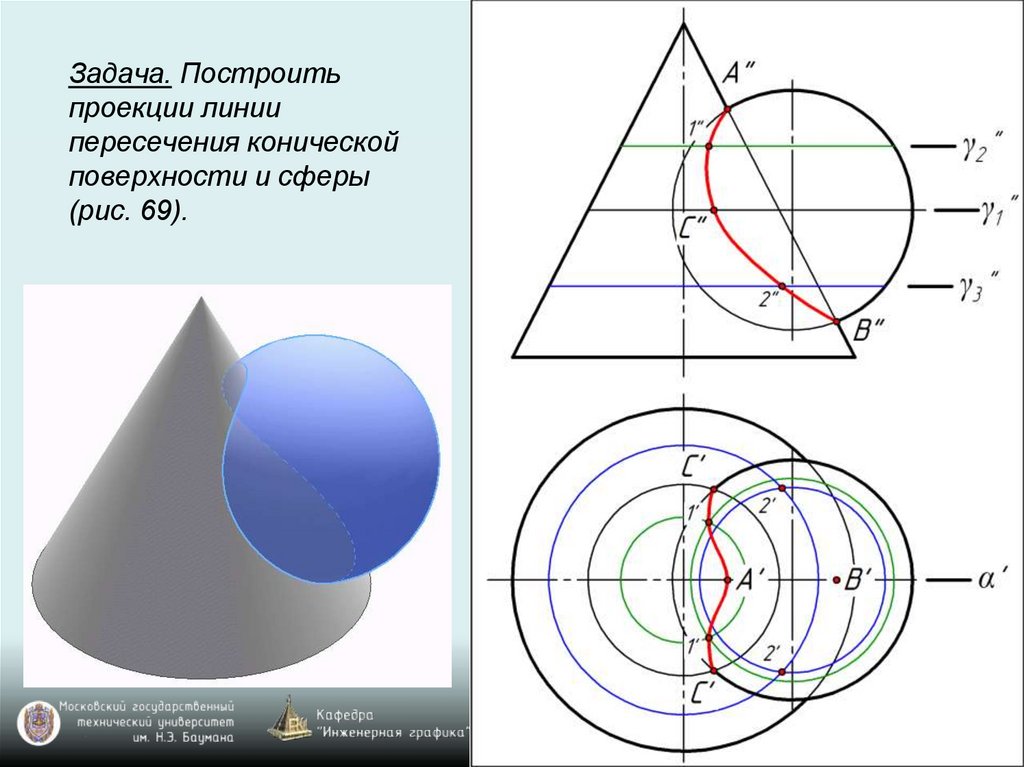
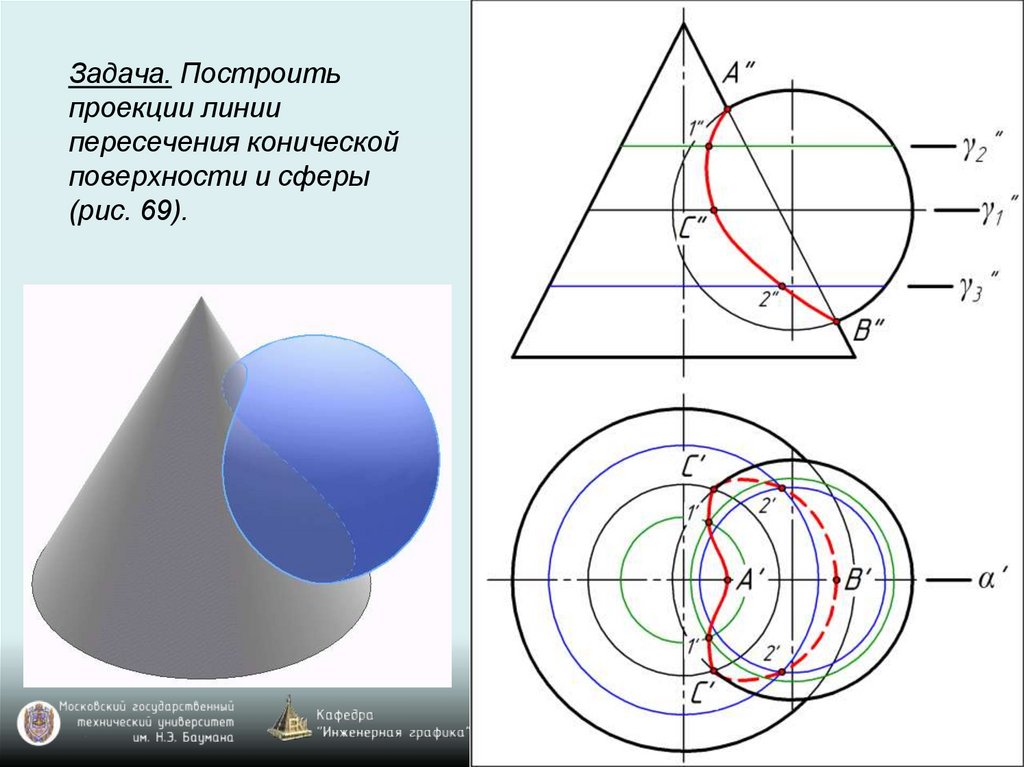
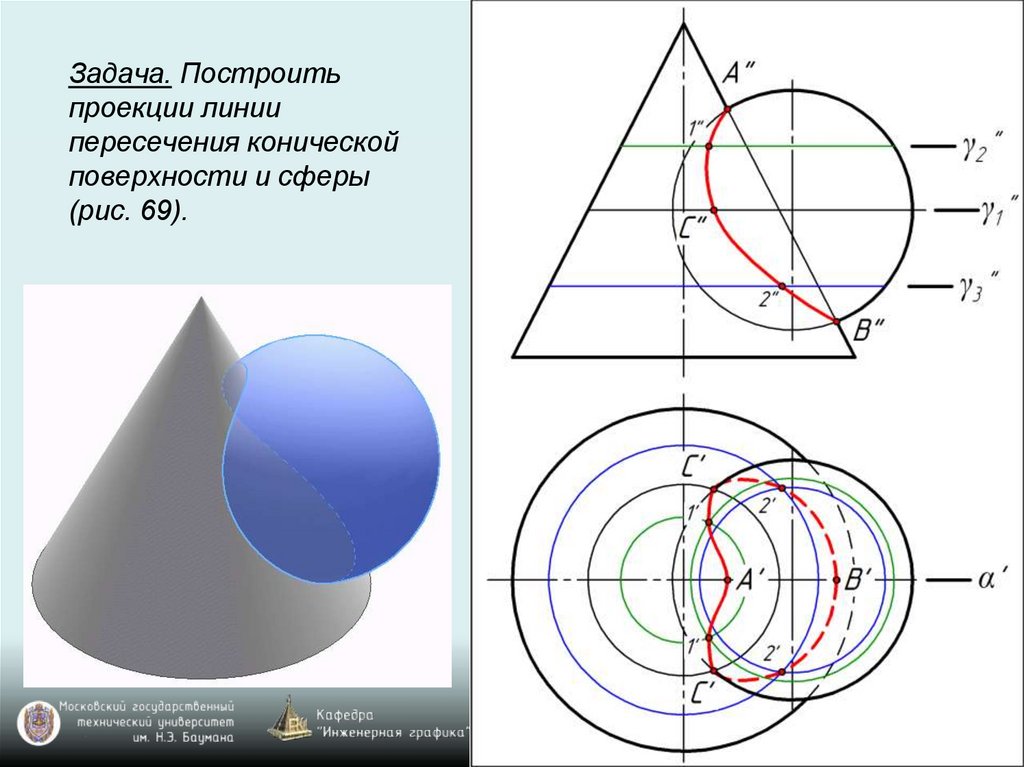
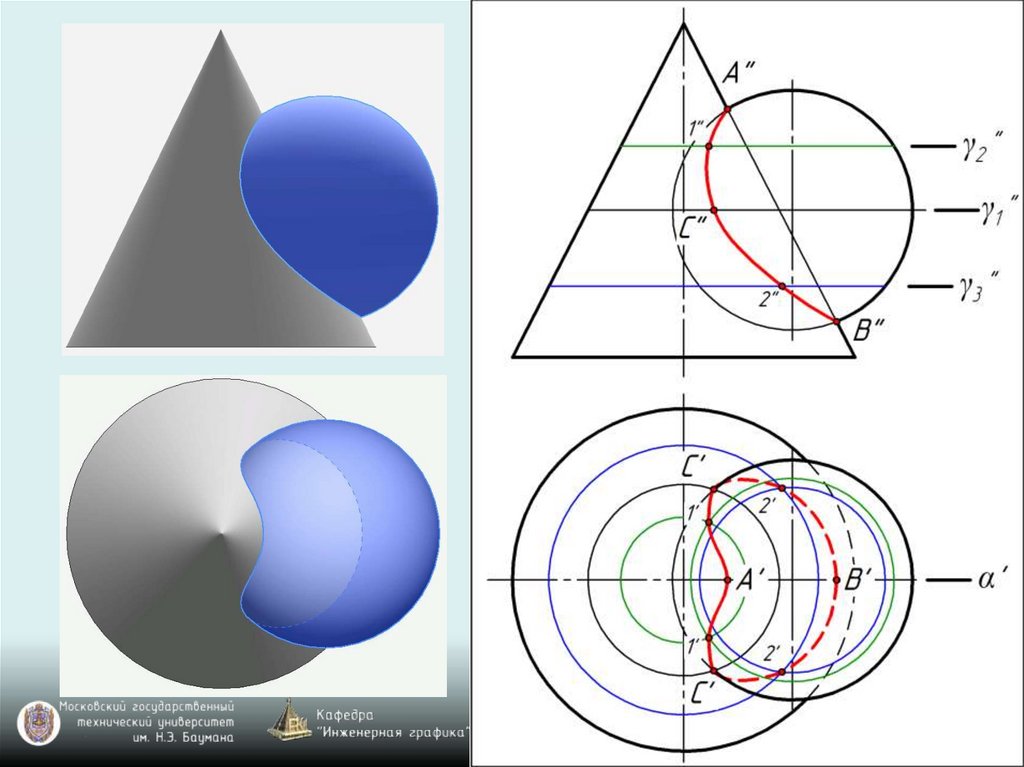
Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

108.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

109.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

110.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

111.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

112.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

113.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

114.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

115.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

116.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

117.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

118.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

119.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

120.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

121.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

122.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

123.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

124.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

125.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

126.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

127.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

128.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

129.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

130.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

131.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

132.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

133.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

134.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

135.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

136.

Задача. Построить
проекции линии
пересечения конической
поверхности и сферы
(рис. 69).

137.

138.

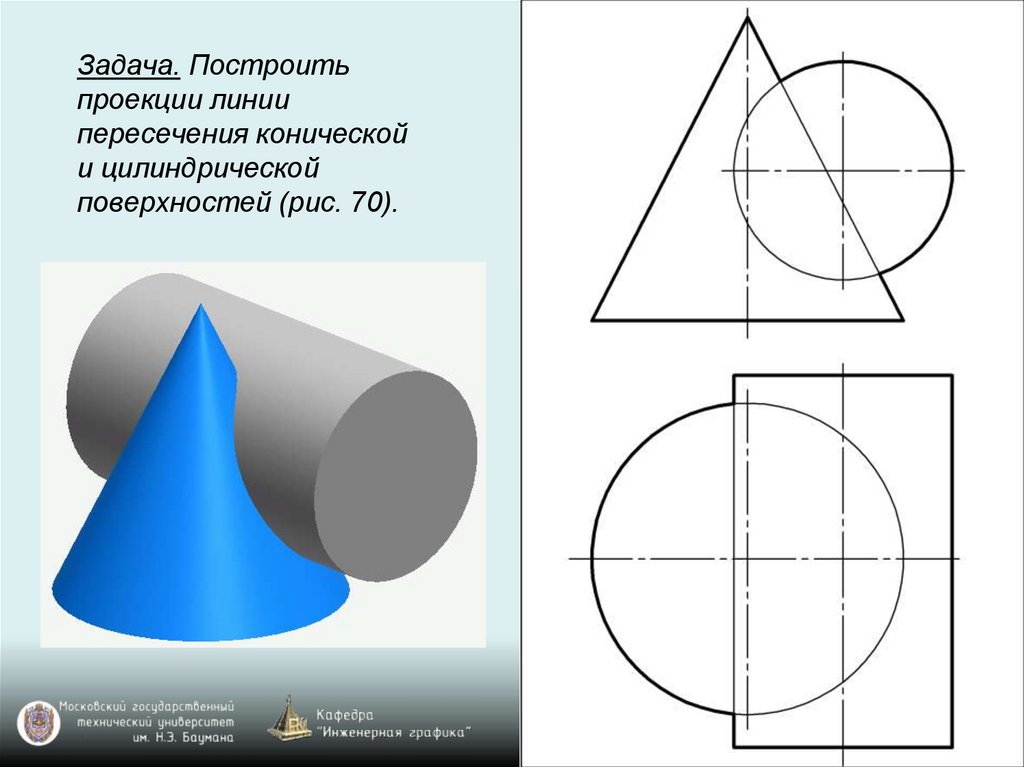
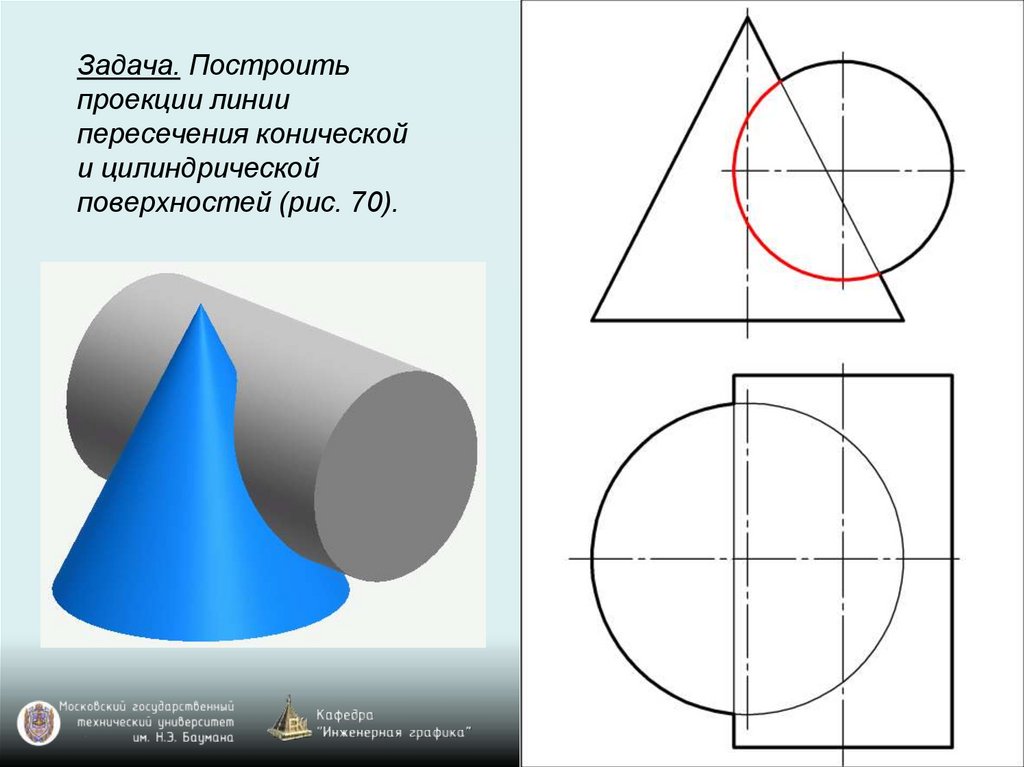
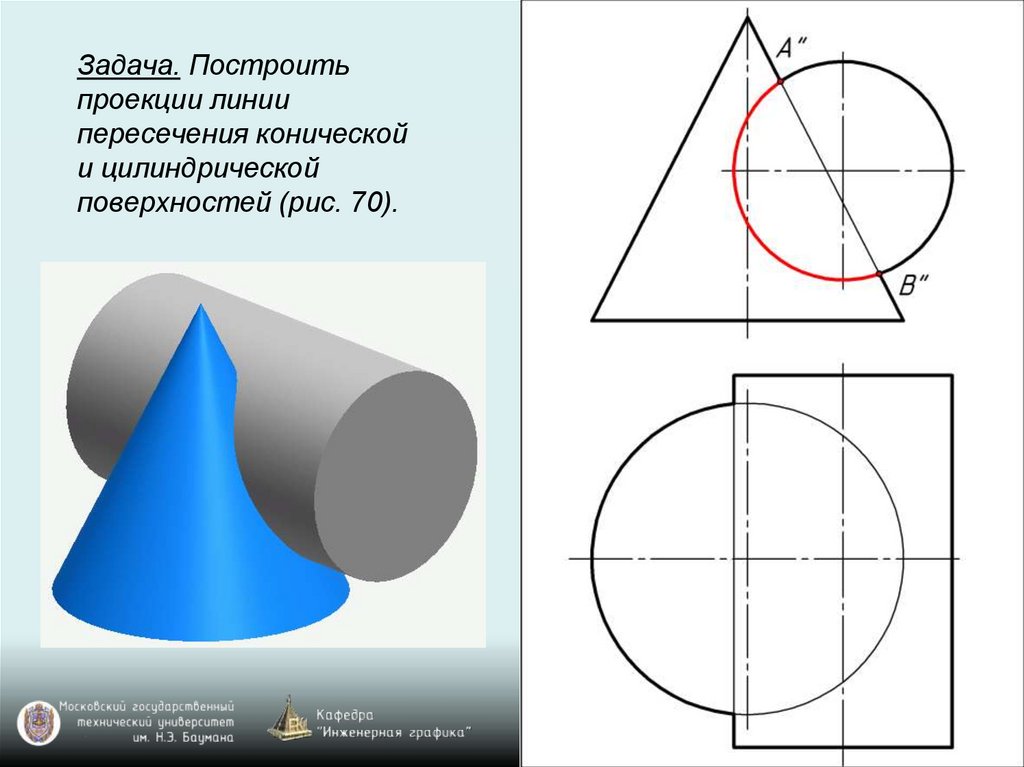
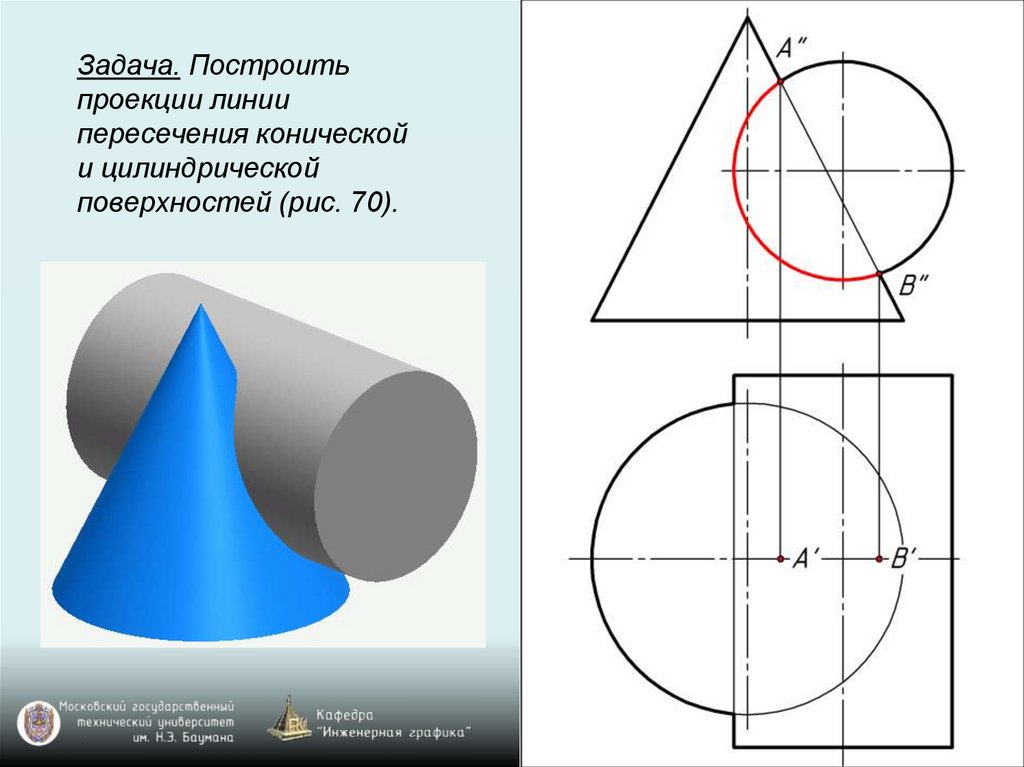
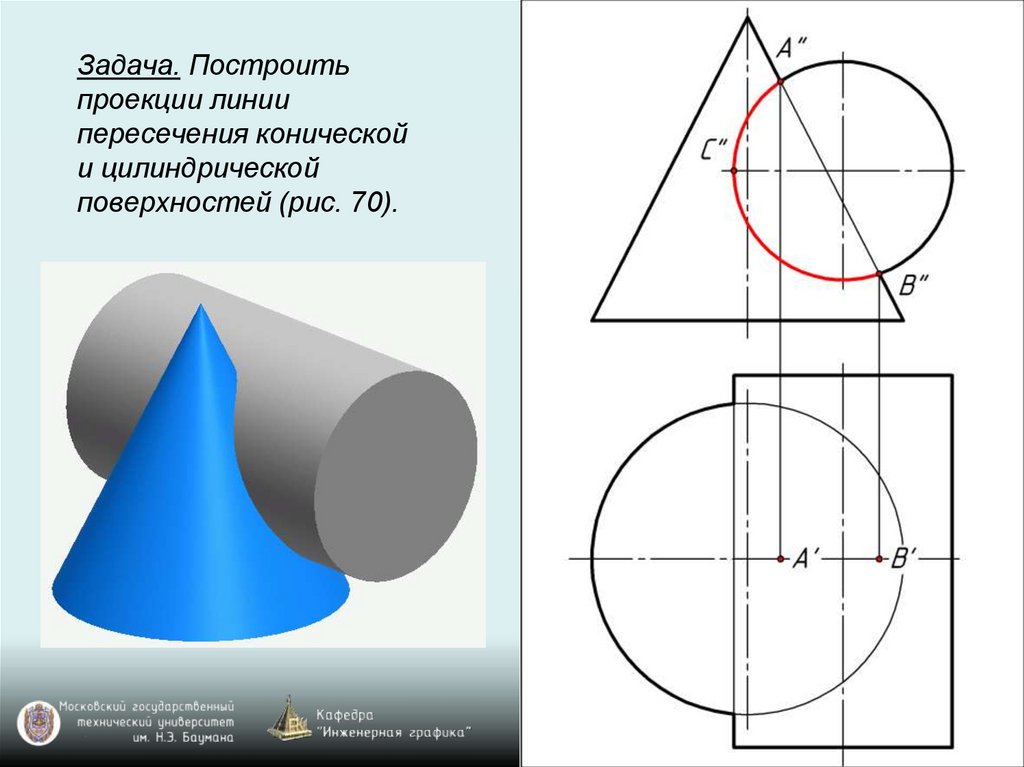
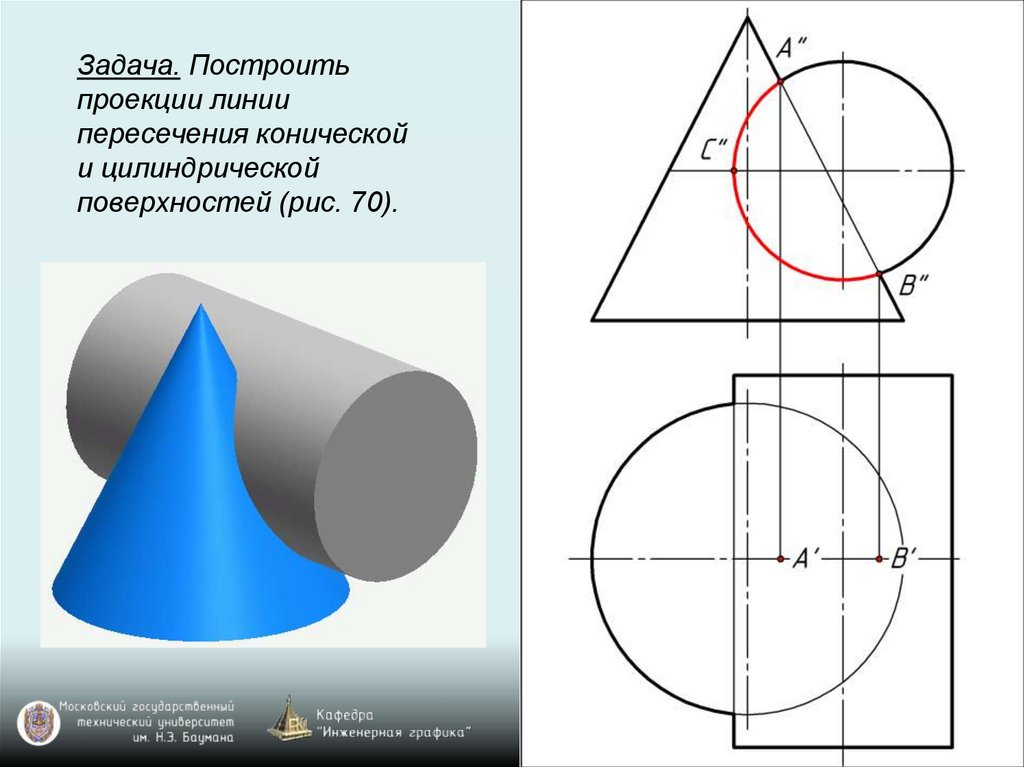
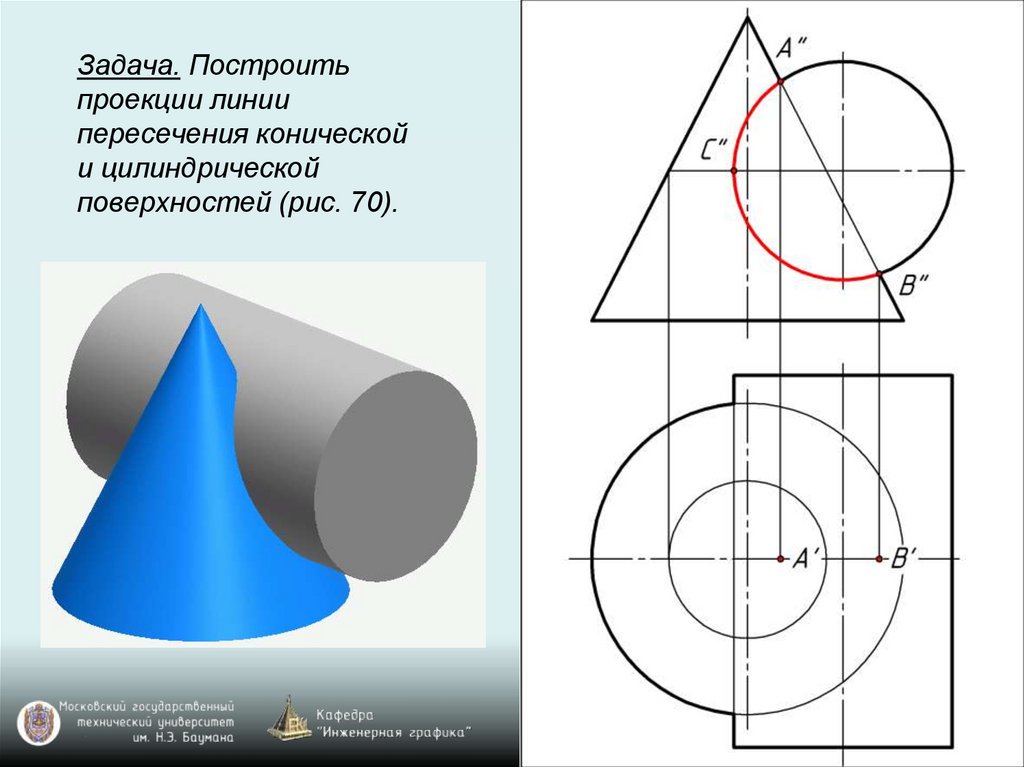
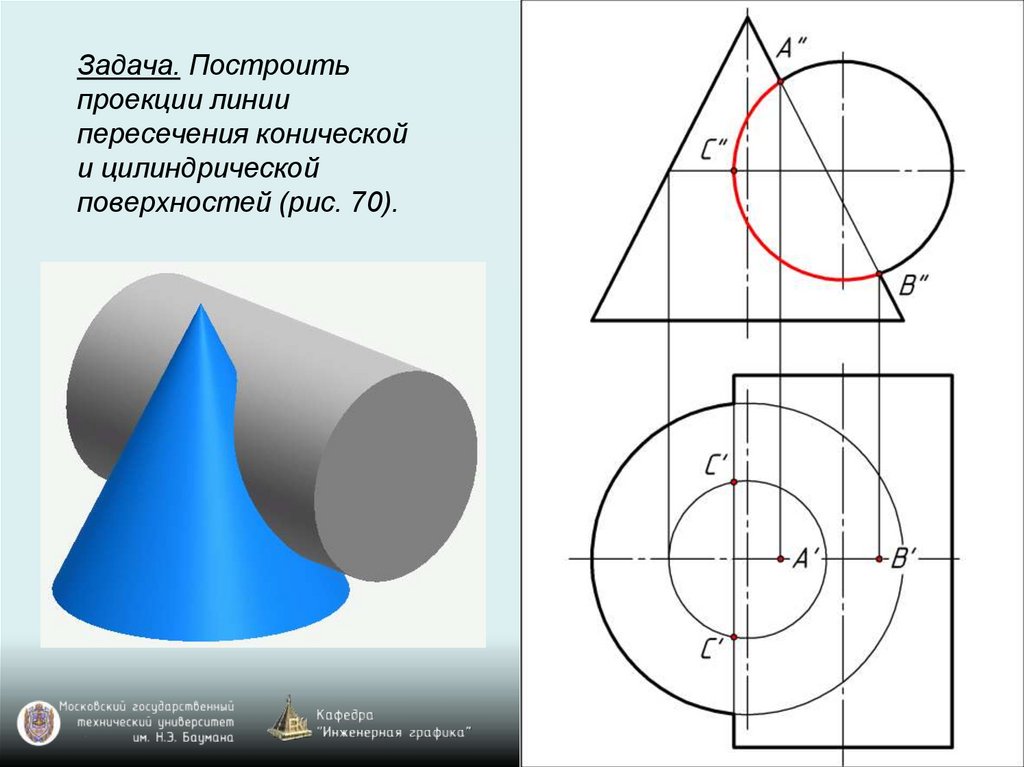
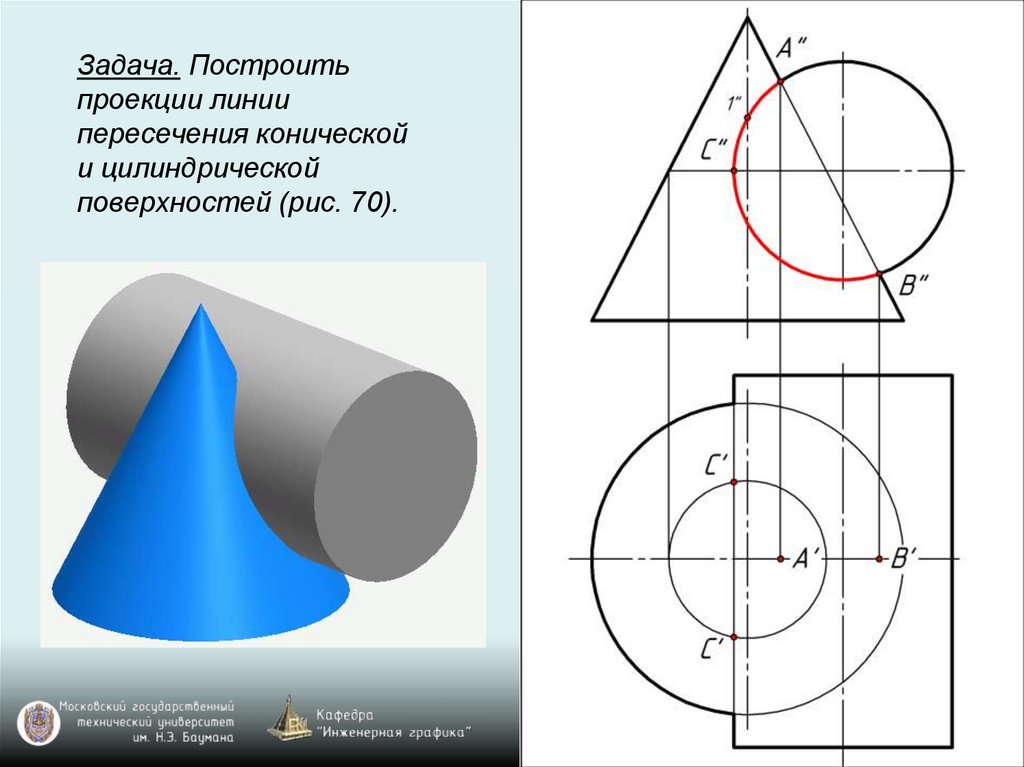
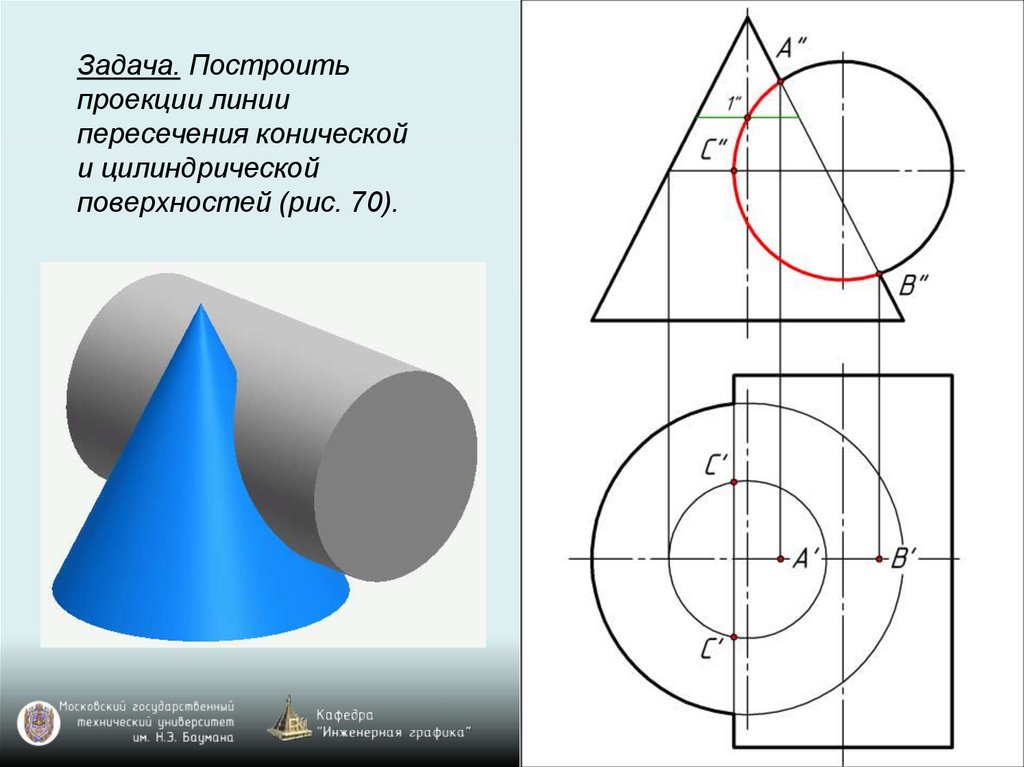
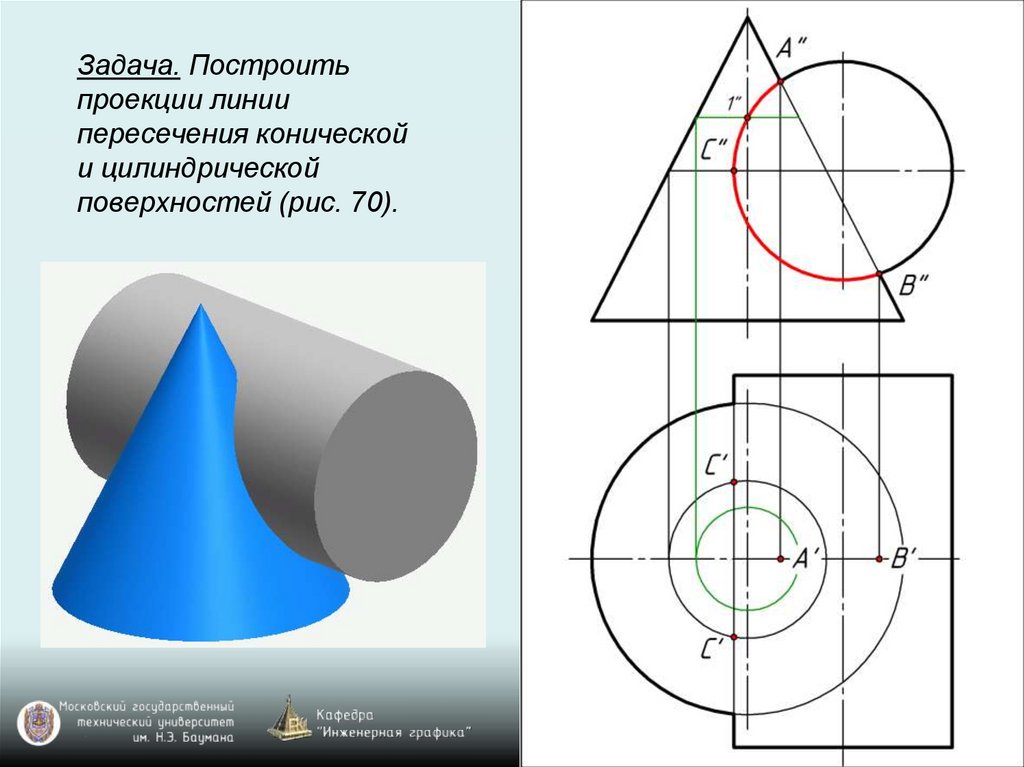
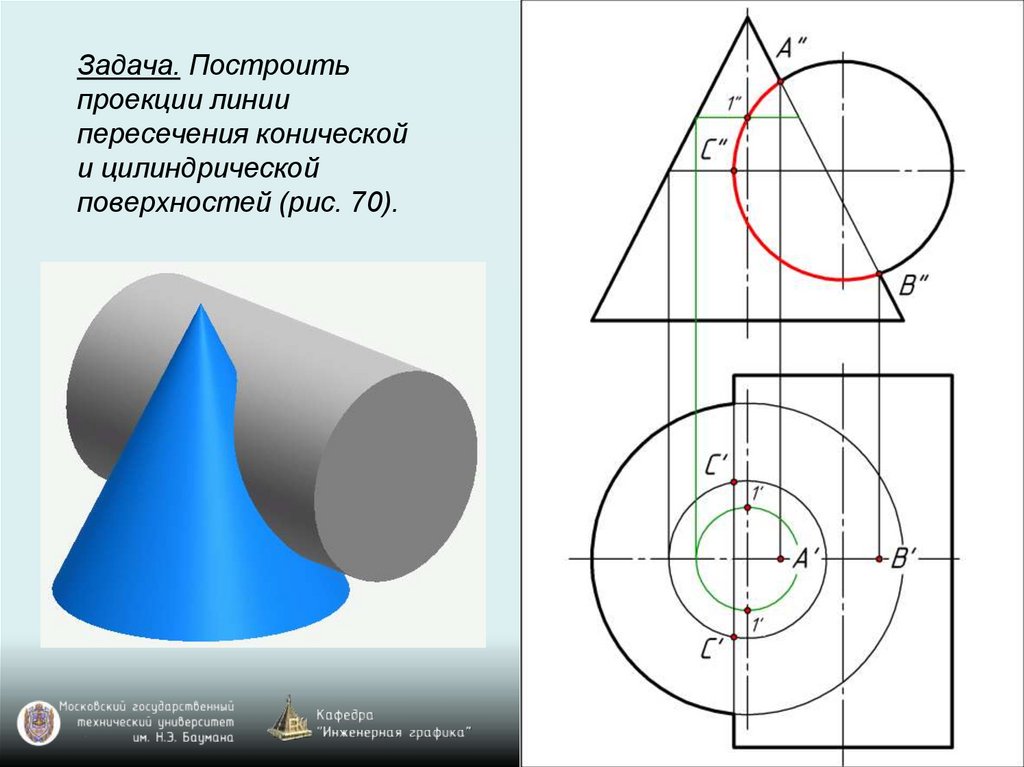
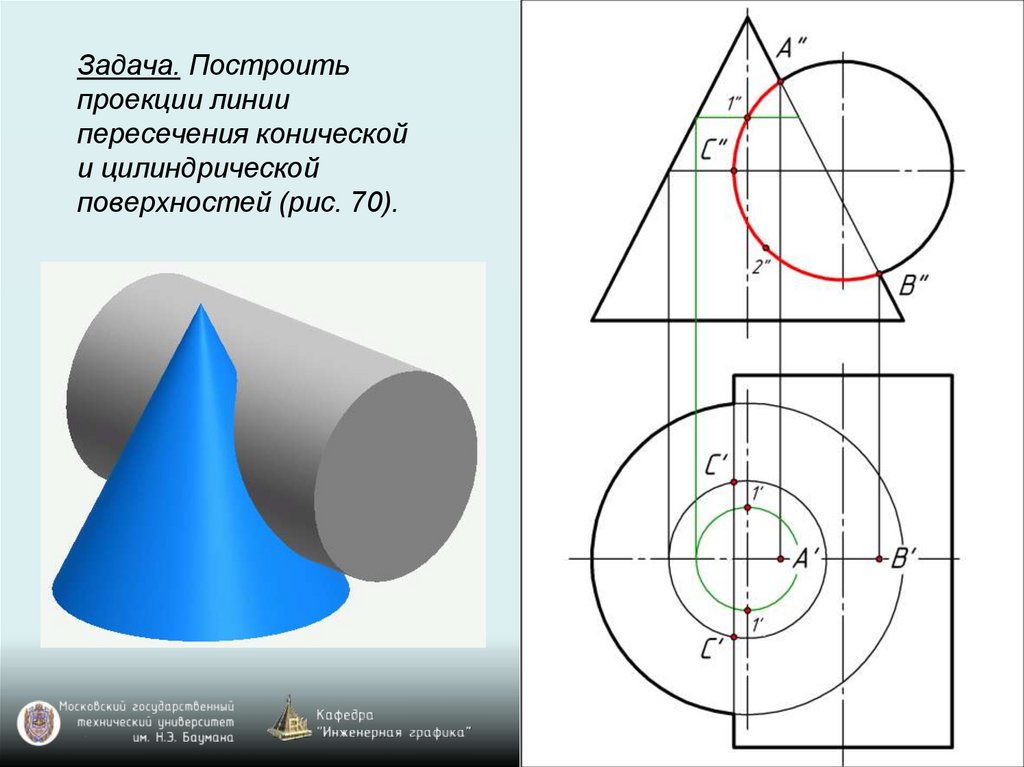
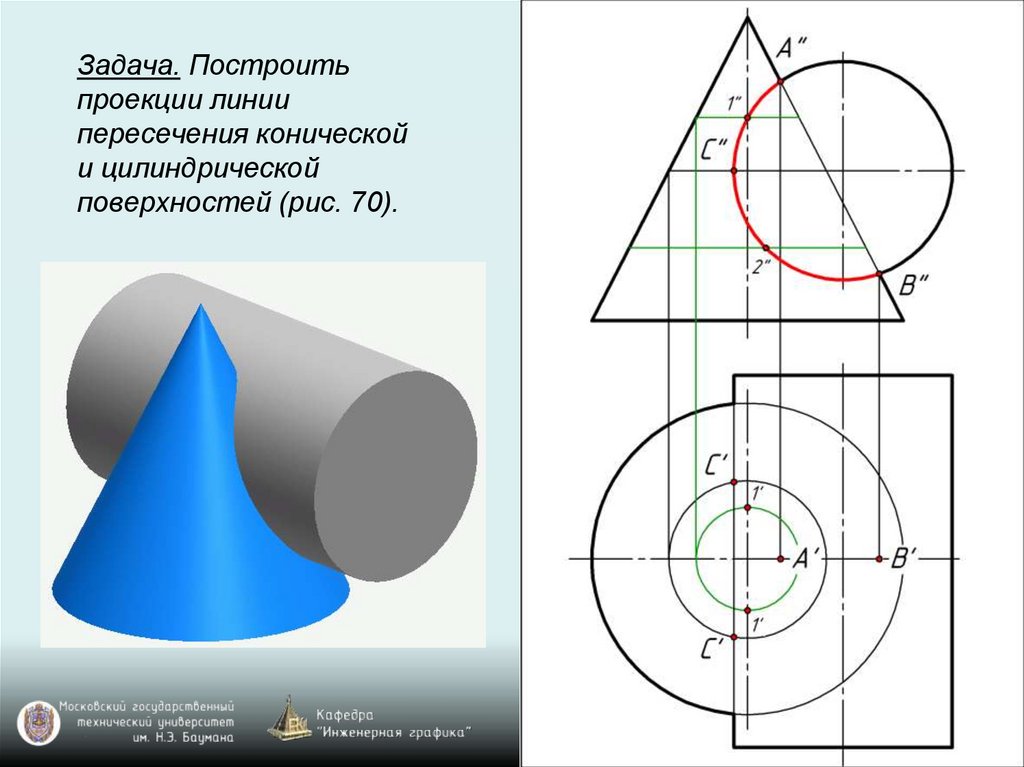
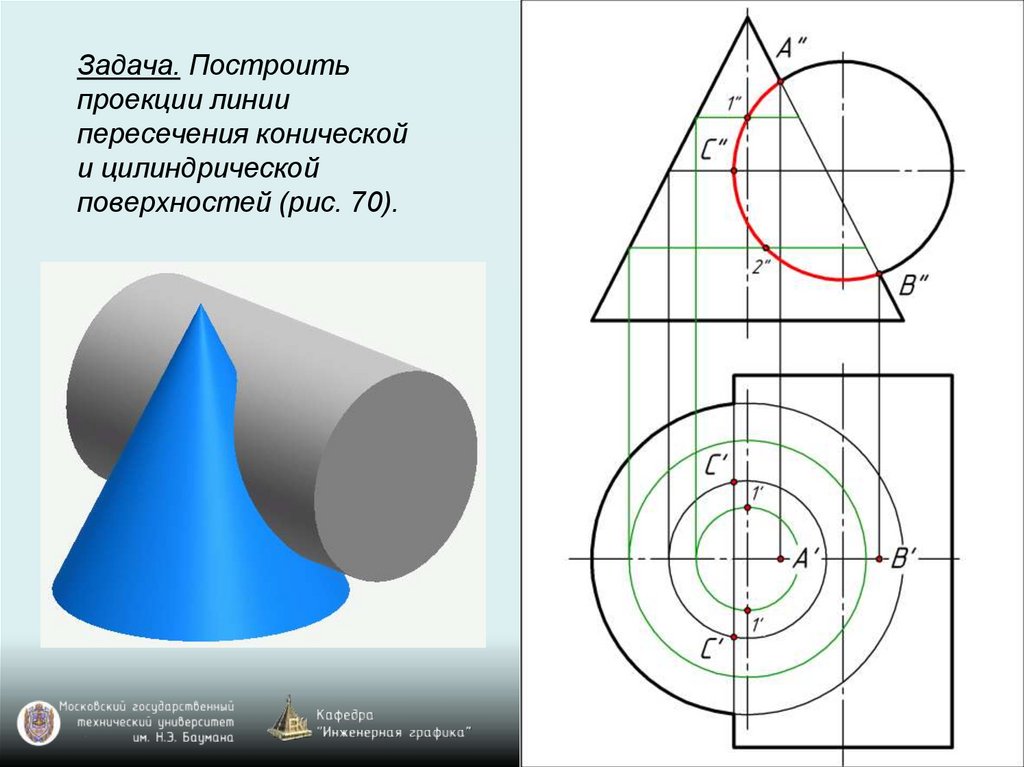
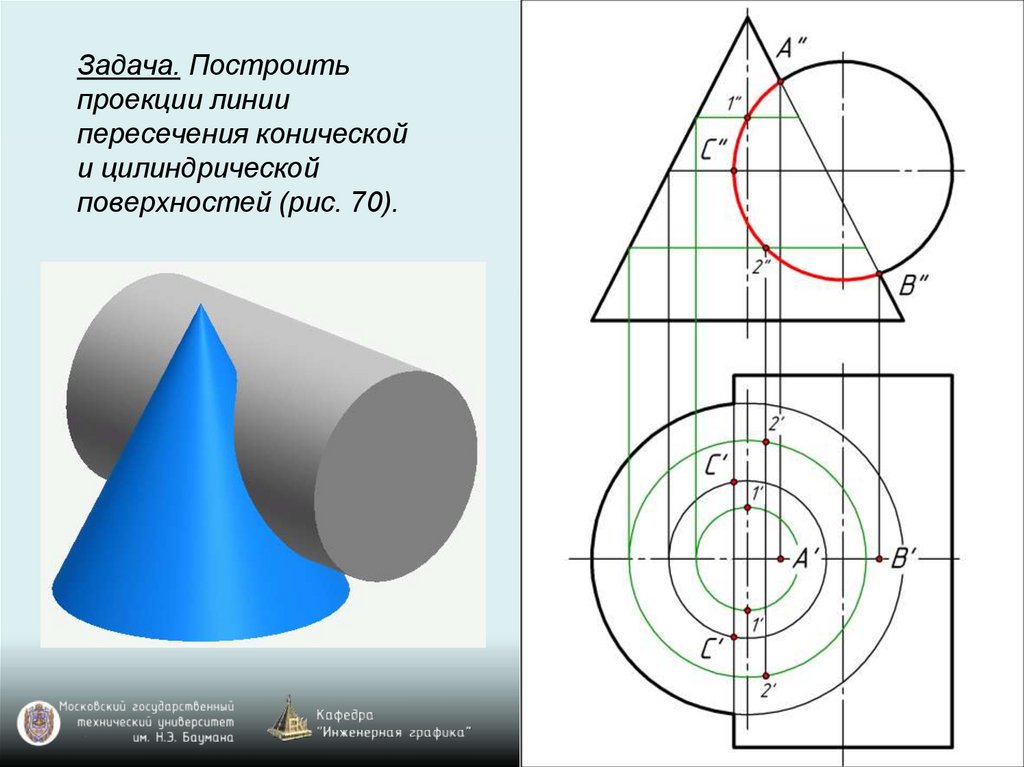
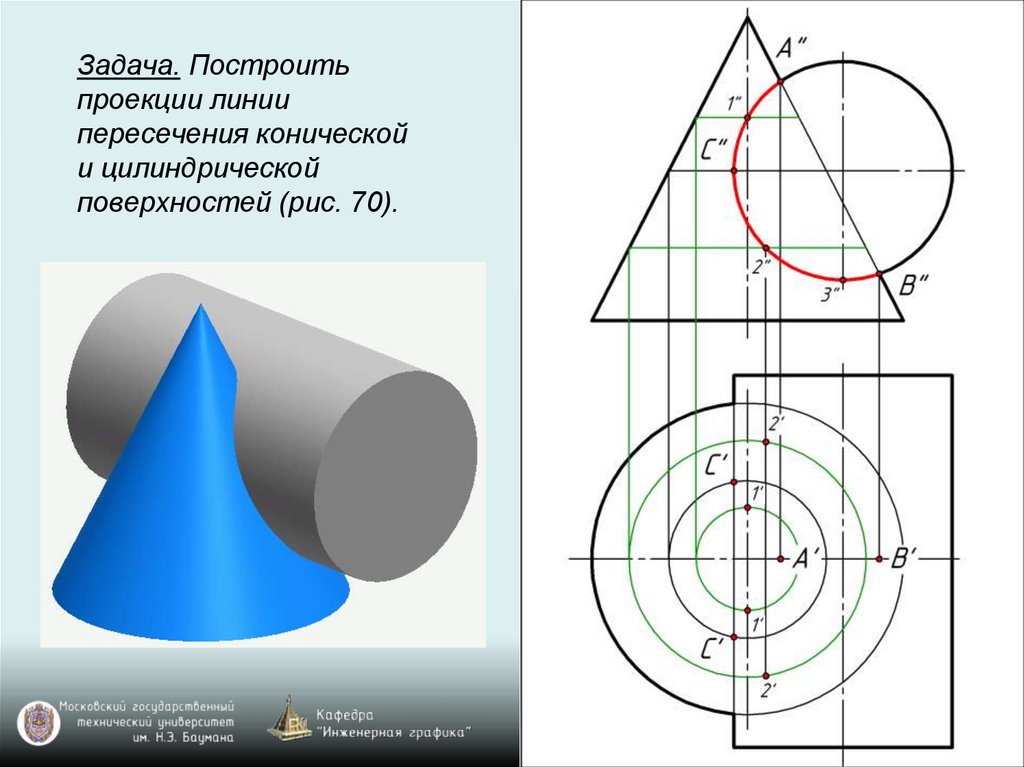
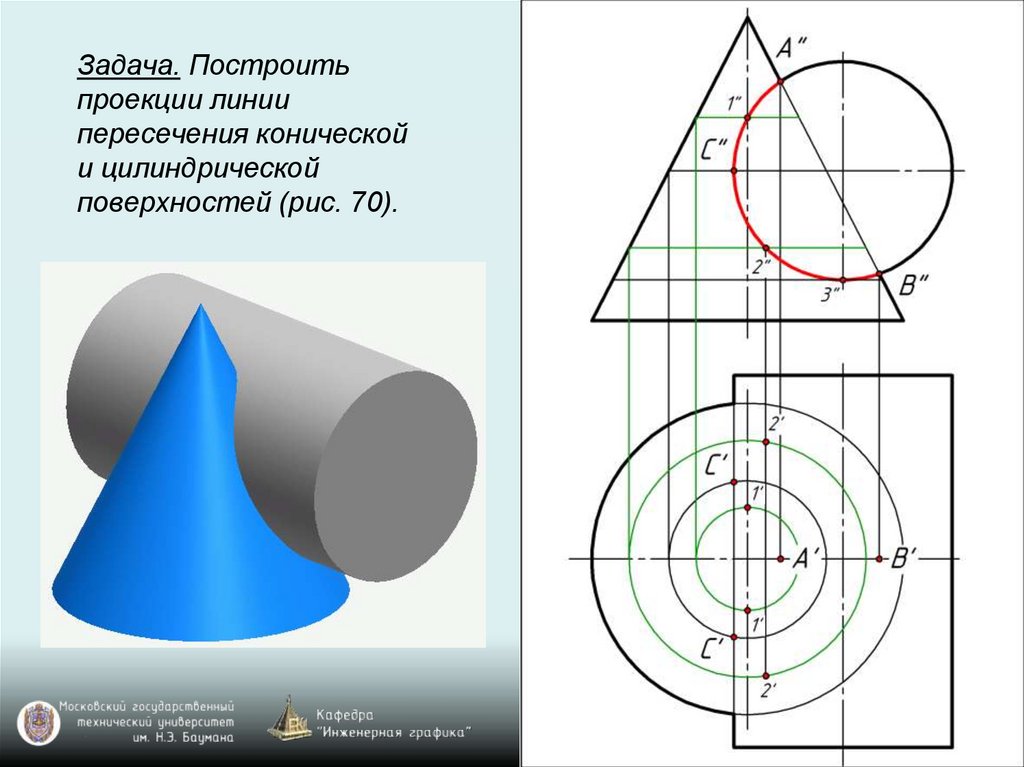
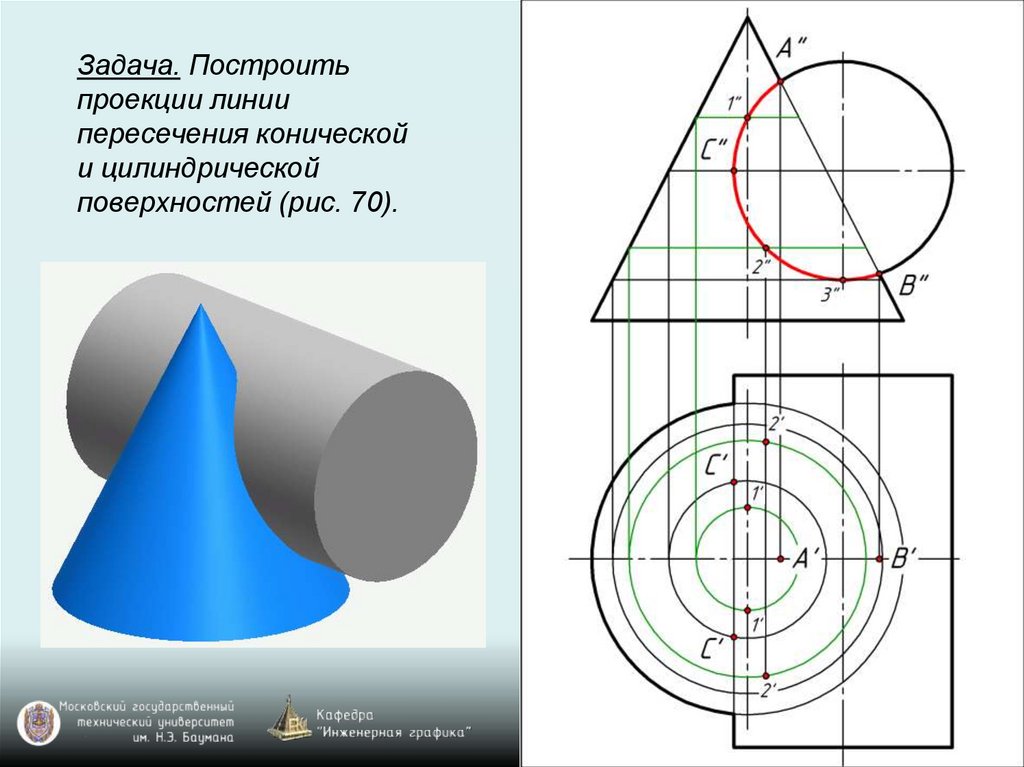
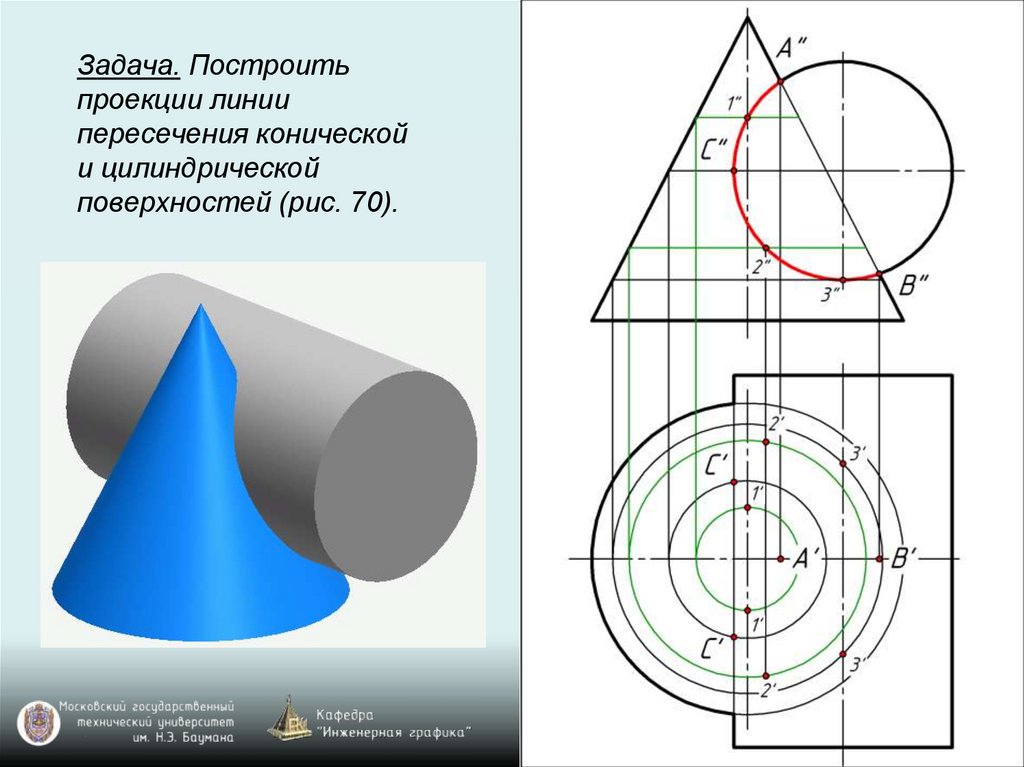
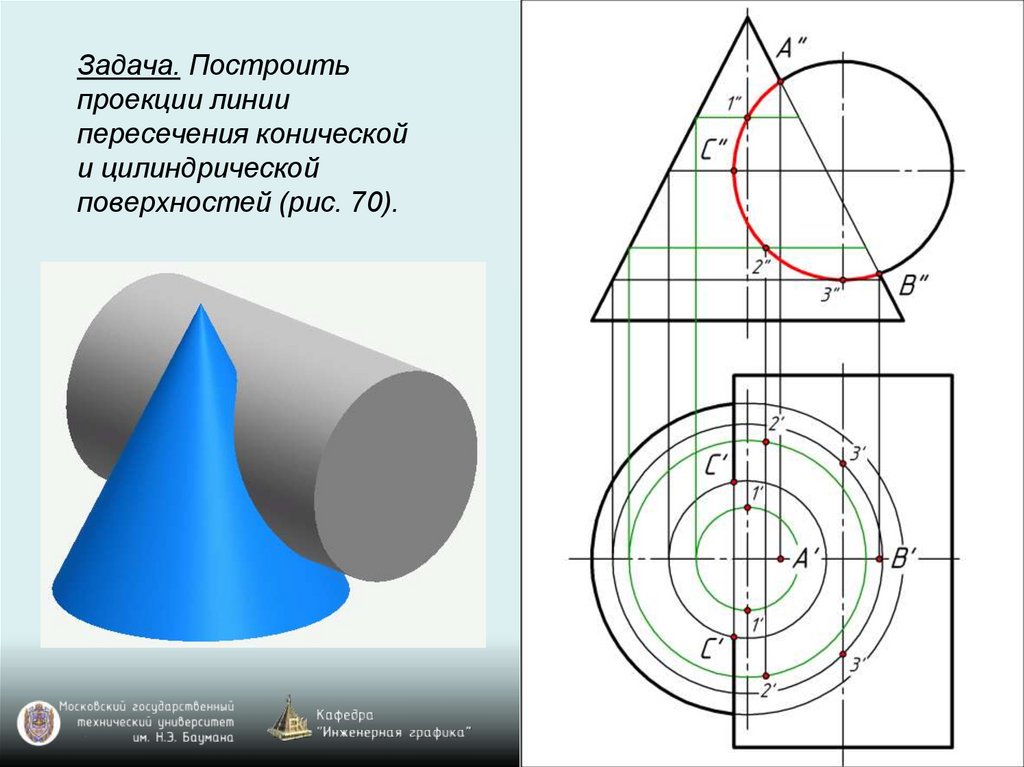
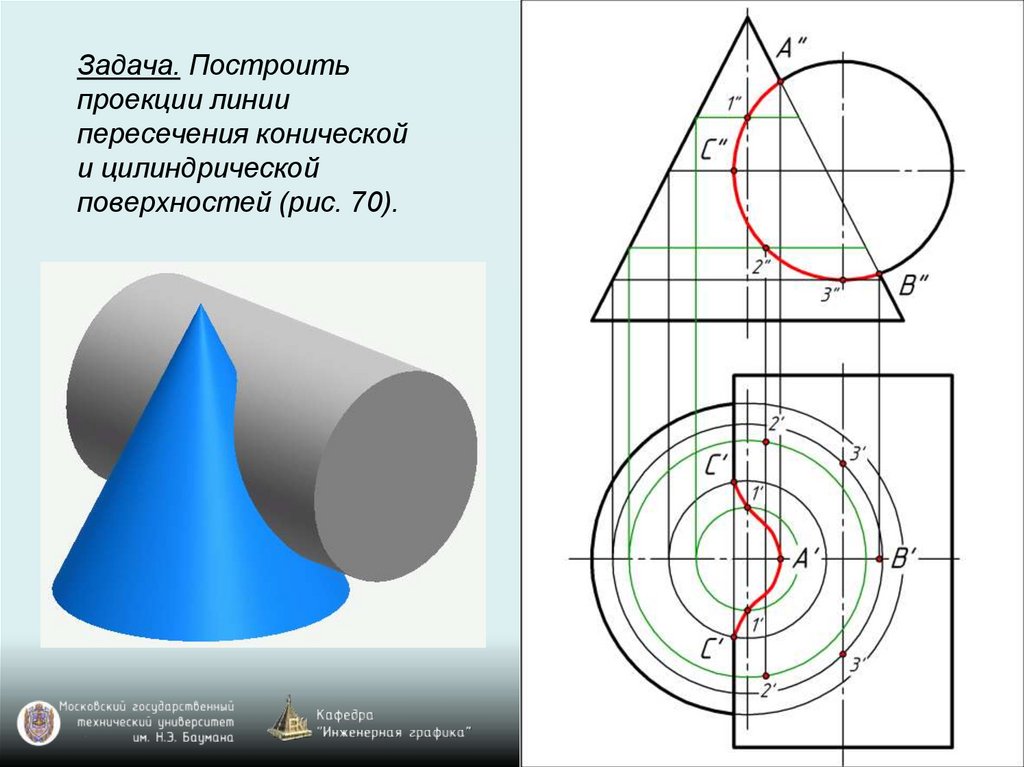
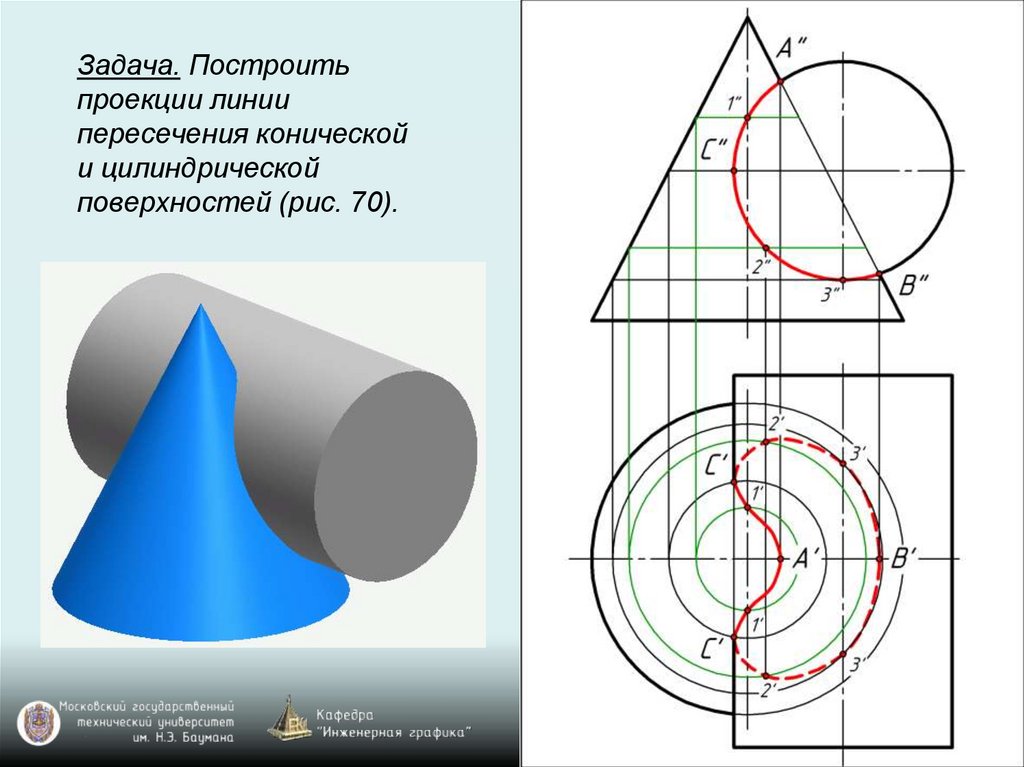
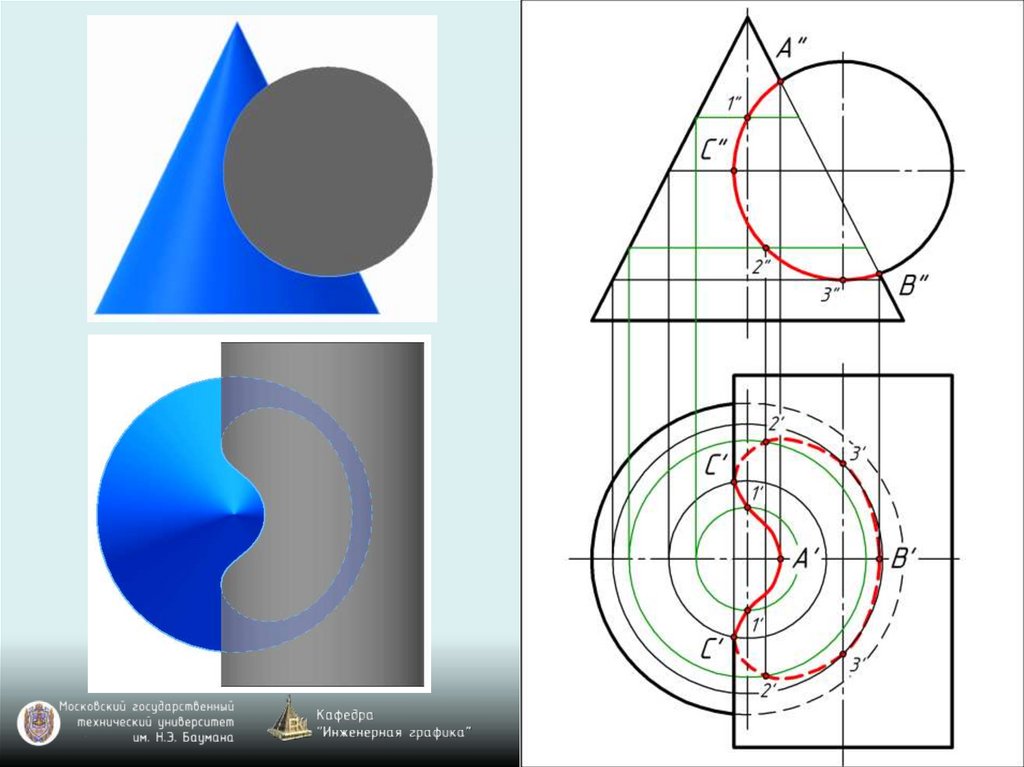
Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

139.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

140.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

141.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

142.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

143.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

144.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

145.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

146.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

147.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

148.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

149.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

150.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

151.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

152.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

153.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

154.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

155.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

156.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

157.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

158.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

159.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

160.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

161.

Задача. Построить
проекции линии
пересечения конической
и цилиндрической
поверхностей (рис. 70).

162.

163.

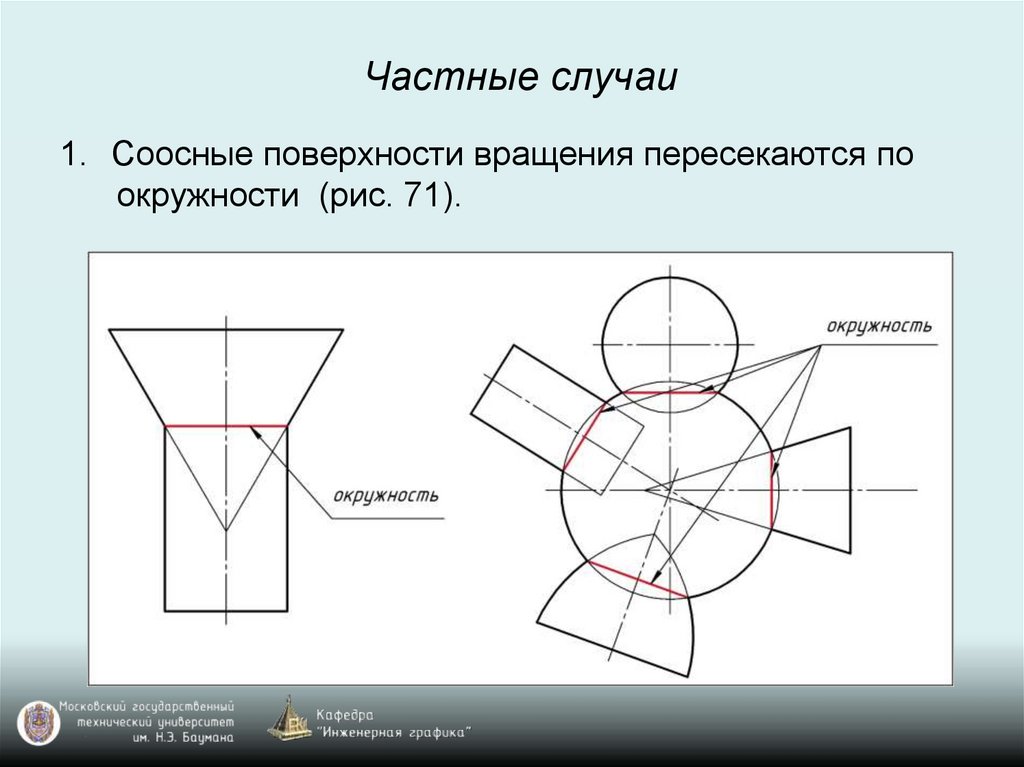
Частные случаи
1. Соосные поверхности вращения пересекаются по
окружности (рис. 71).

164.

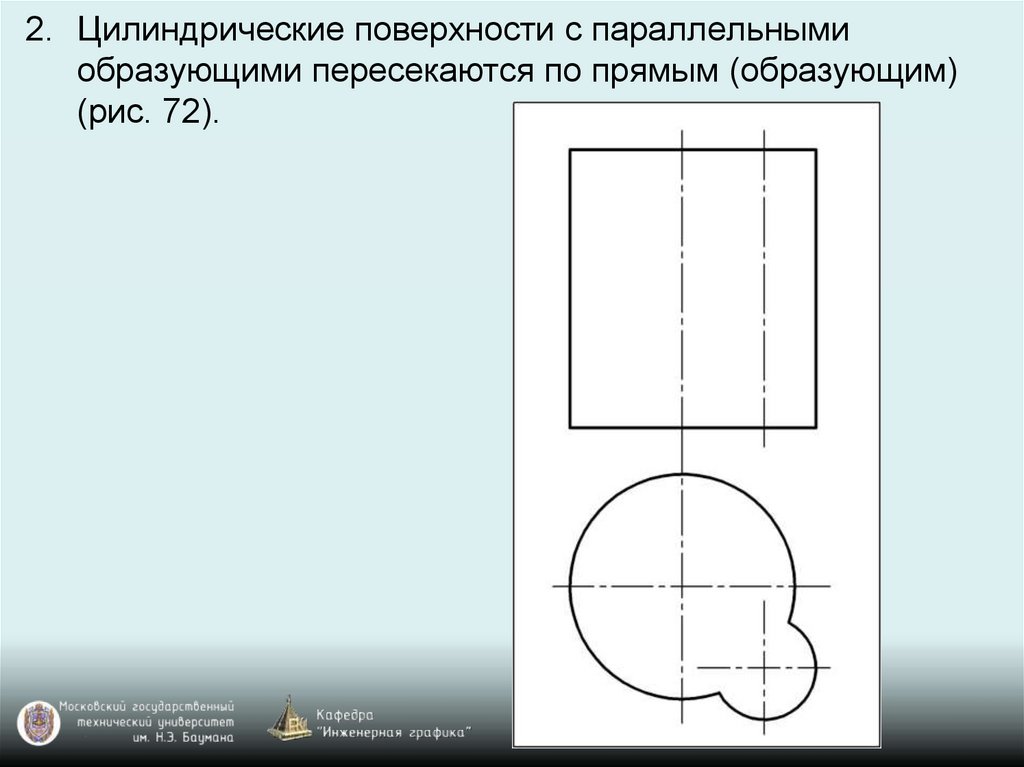
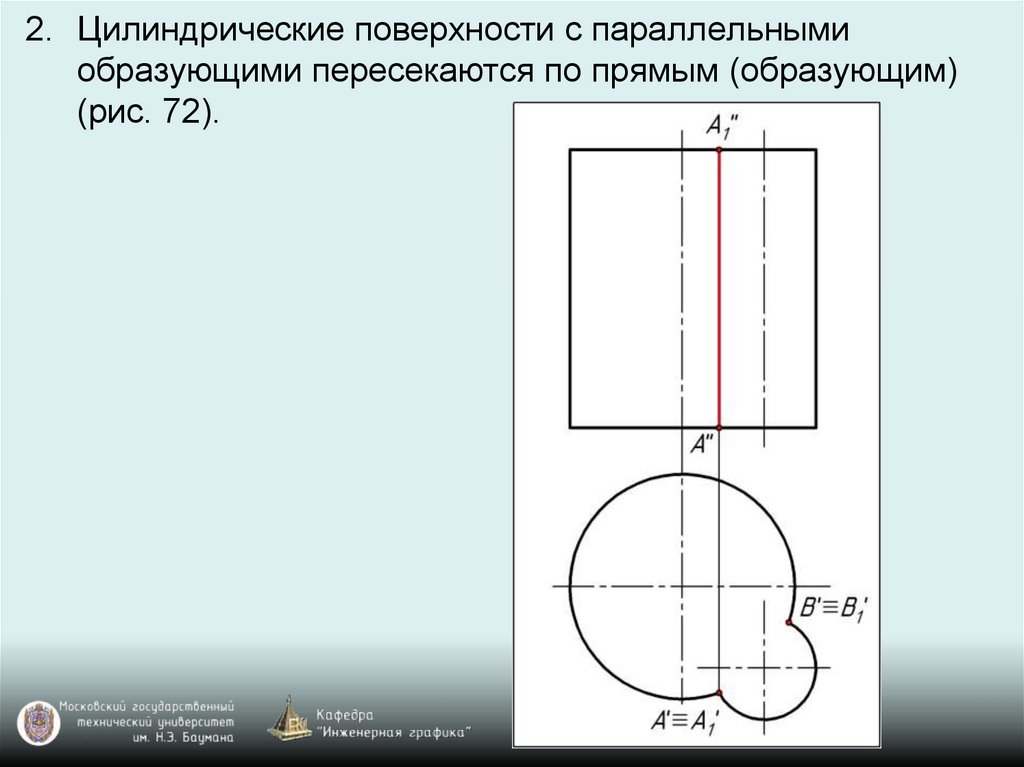
2. Цилиндрические поверхности с параллельными
образующими пересекаются по прямым (образующим)
(рис. 72).

165.

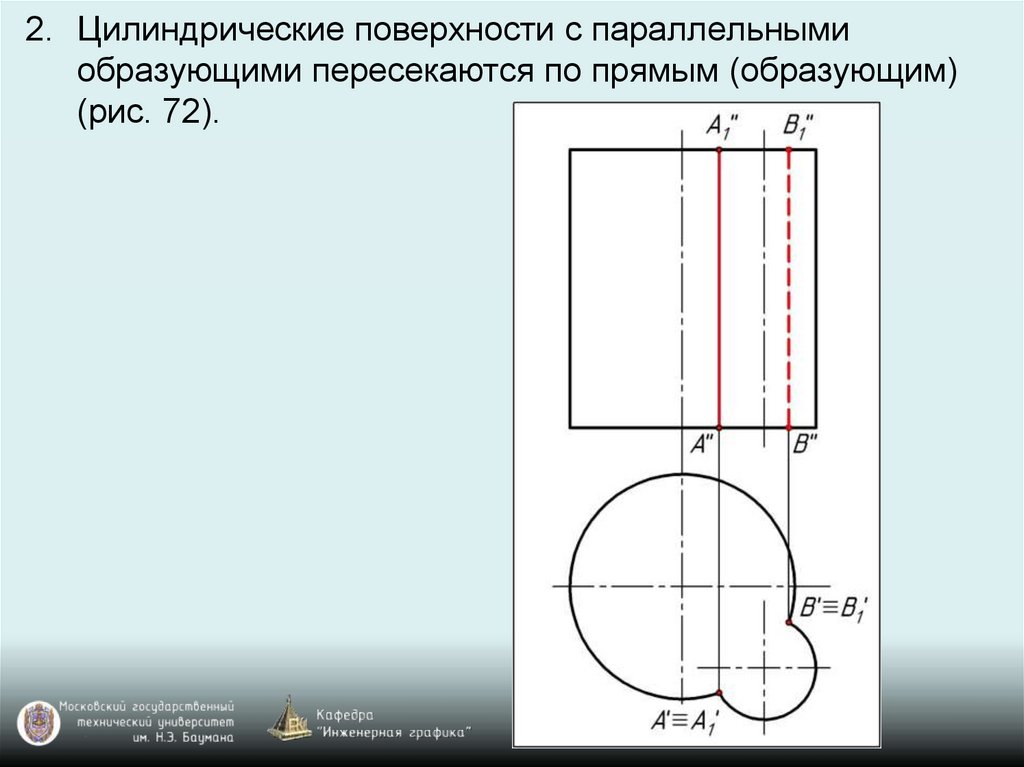
2. Цилиндрические поверхности с параллельными
образующими пересекаются по прямым (образующим)
(рис. 72).

166.

2. Цилиндрические поверхности с параллельными
образующими пересекаются по прямым (образующим)
(рис. 72).

167.

2. Цилиндрические поверхности с параллельными
образующими пересекаются по прямым (образующим)
(рис. 72).

168.

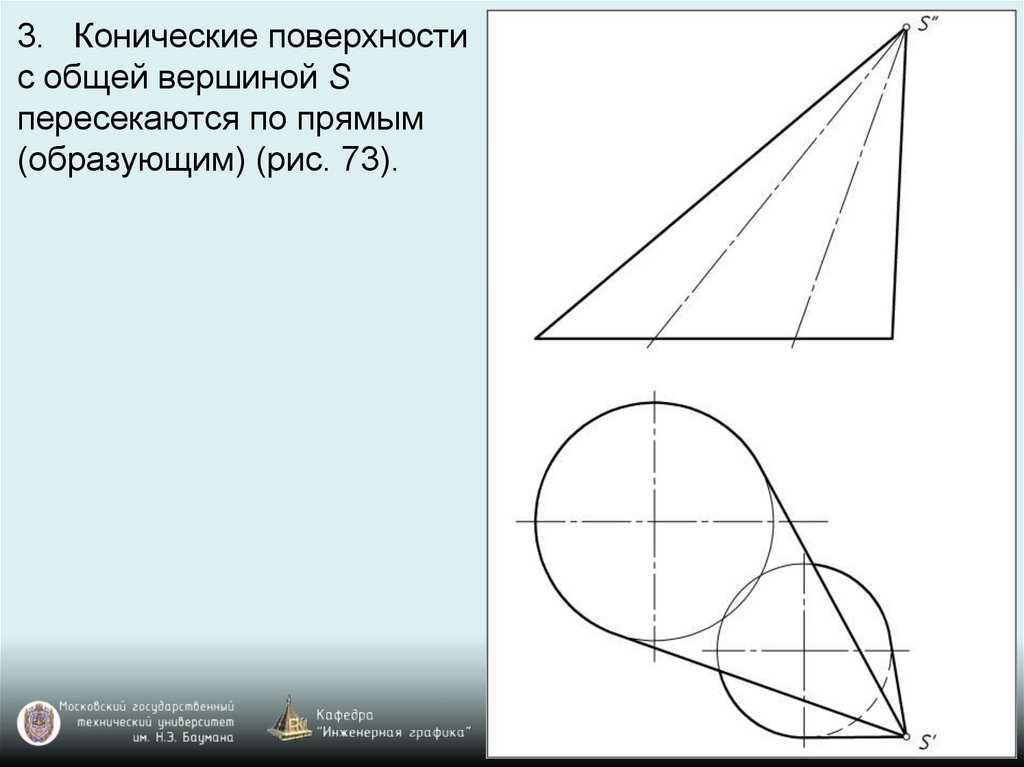
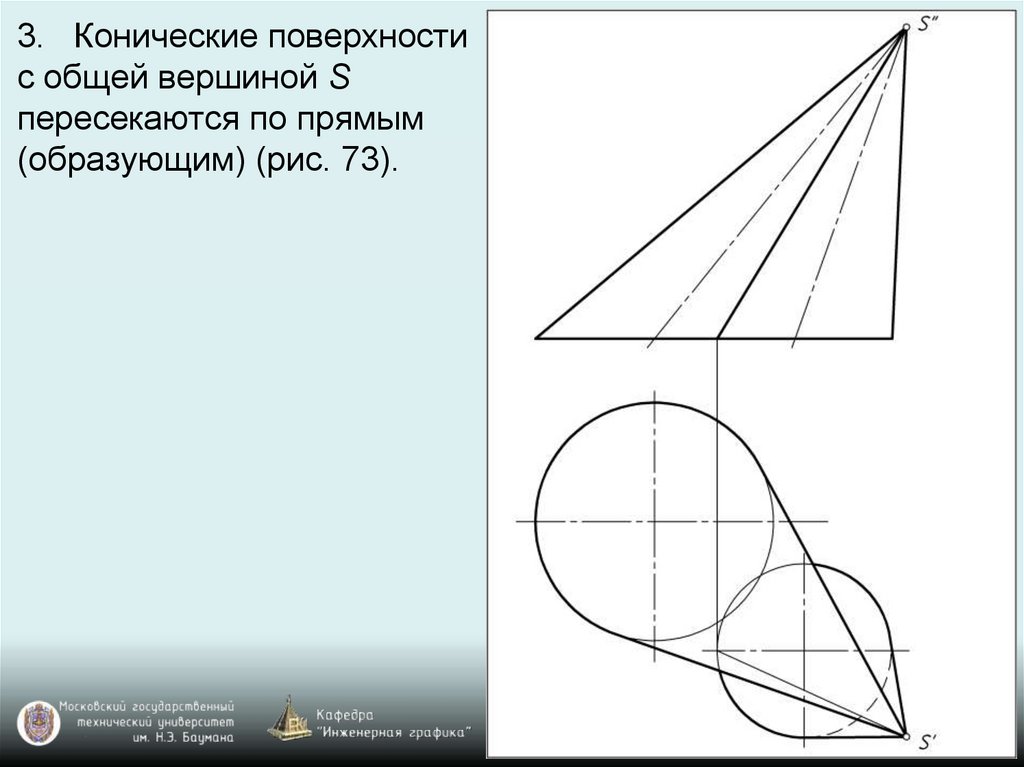
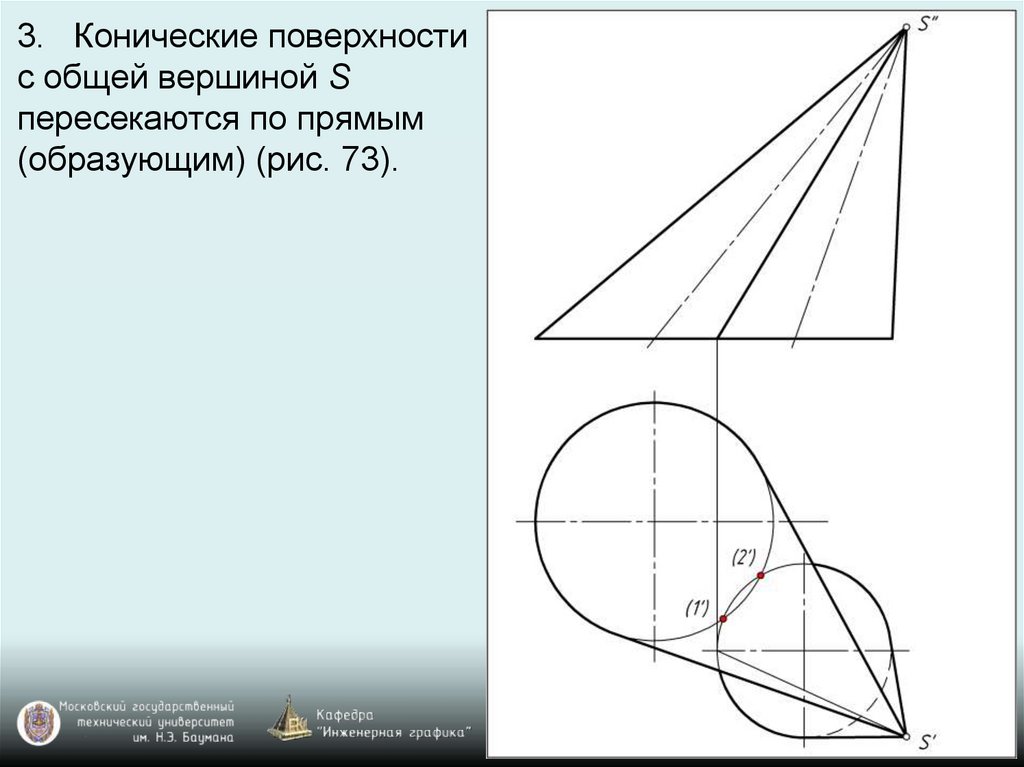
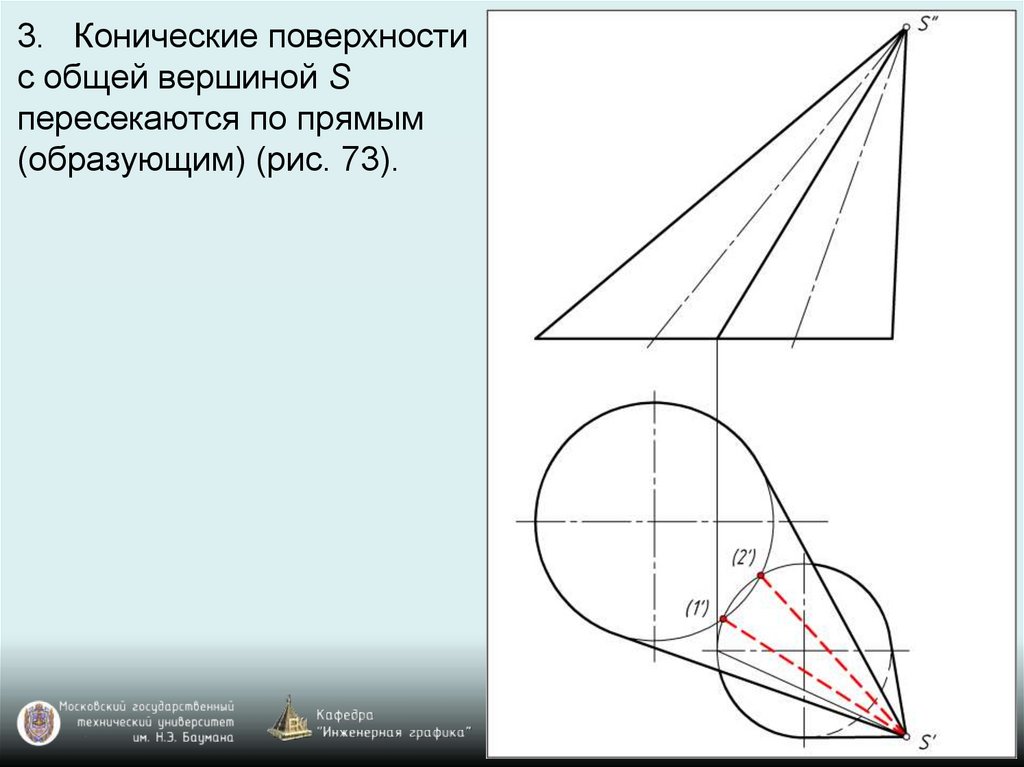
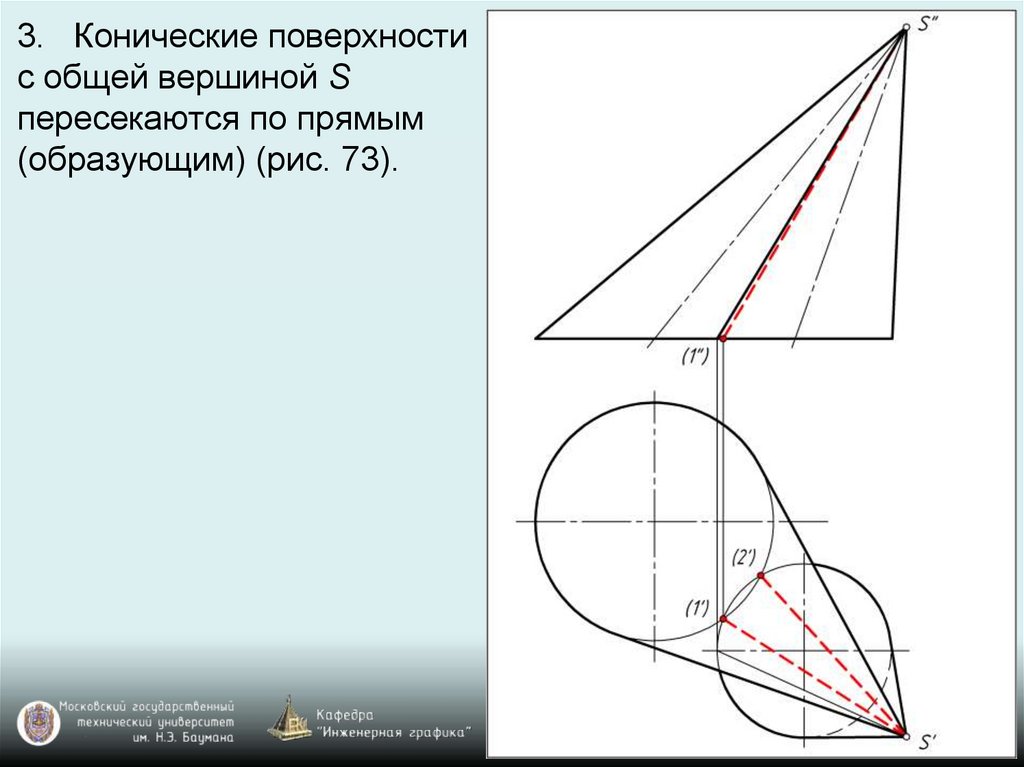
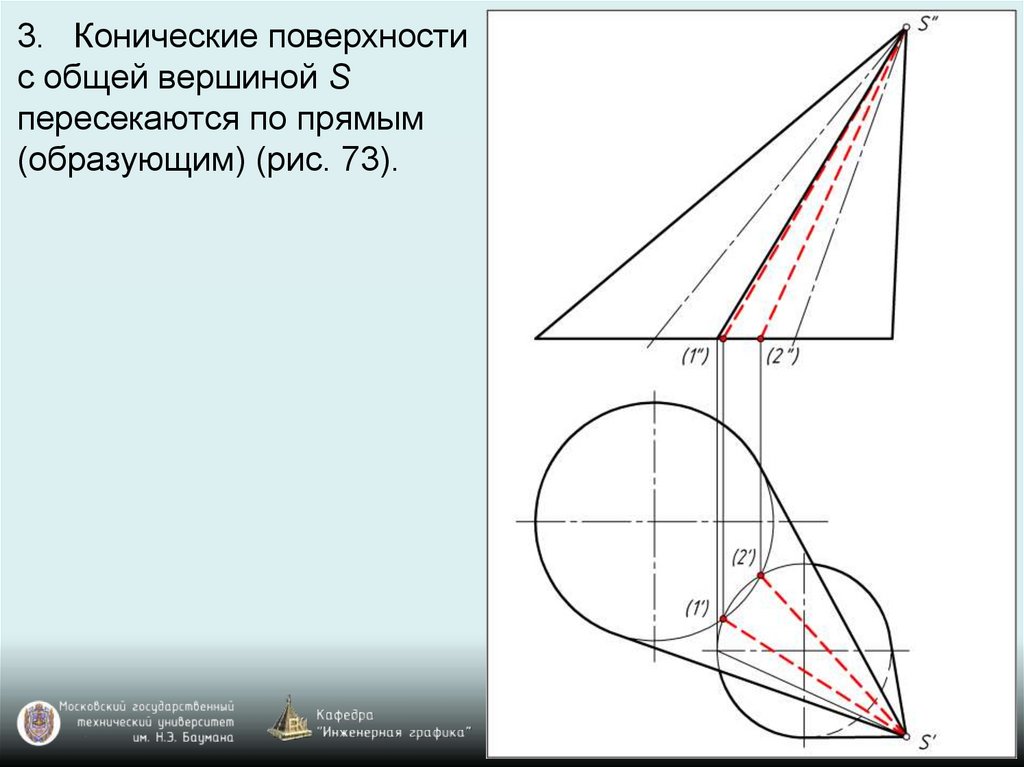
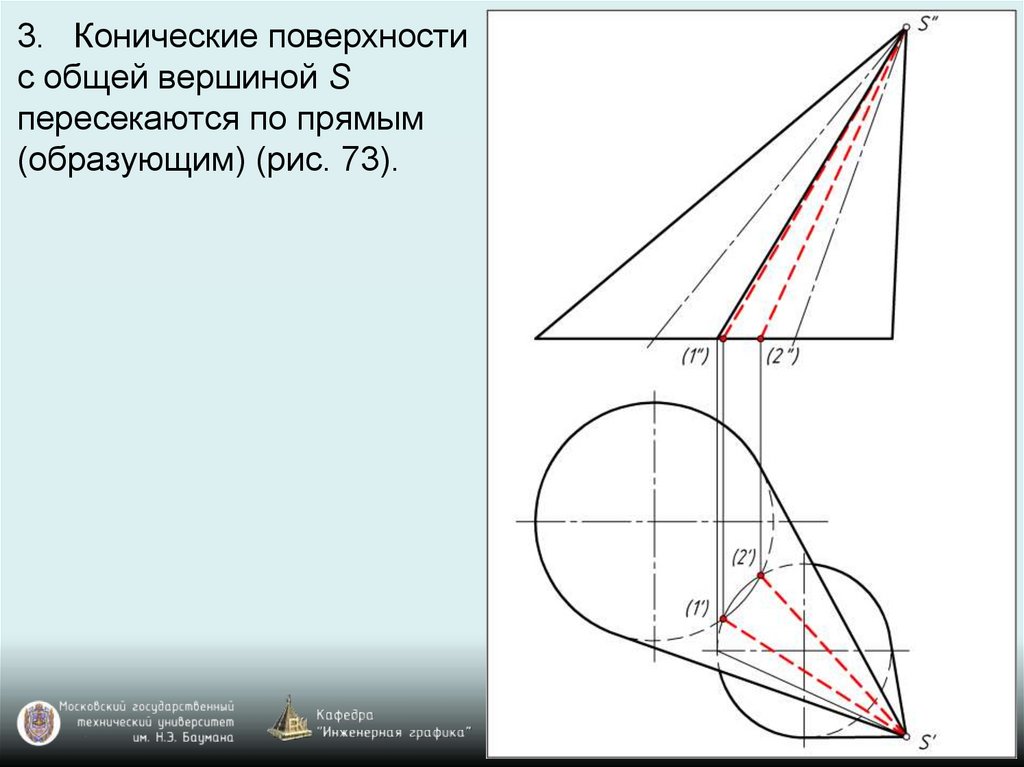
3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

169.

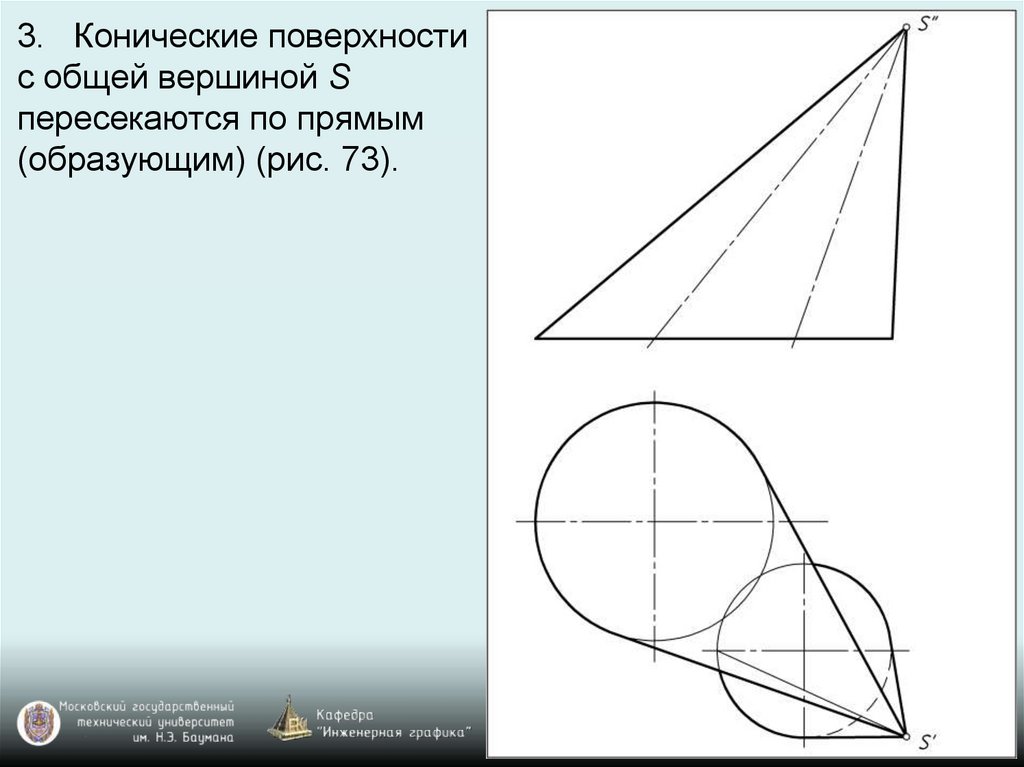
3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

170.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

171.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

172.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

173.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

174.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

175.

3. Конические поверхности
с общей вершиной S
пересекаются по прямым
(образующим) (рис. 73).

176.

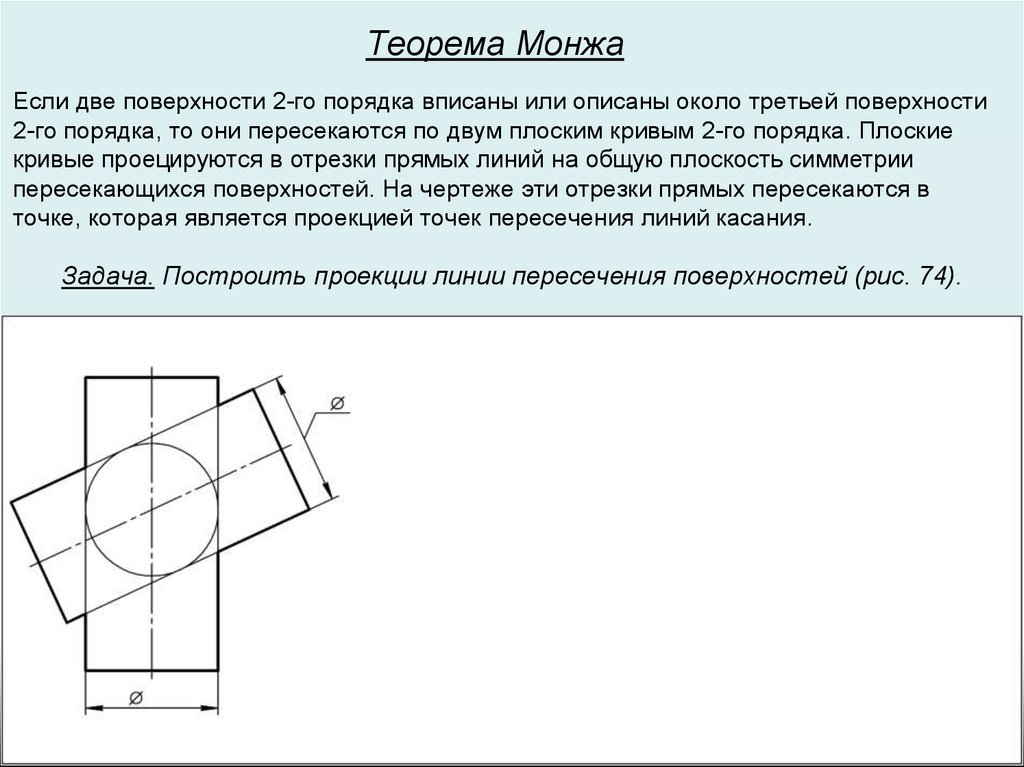
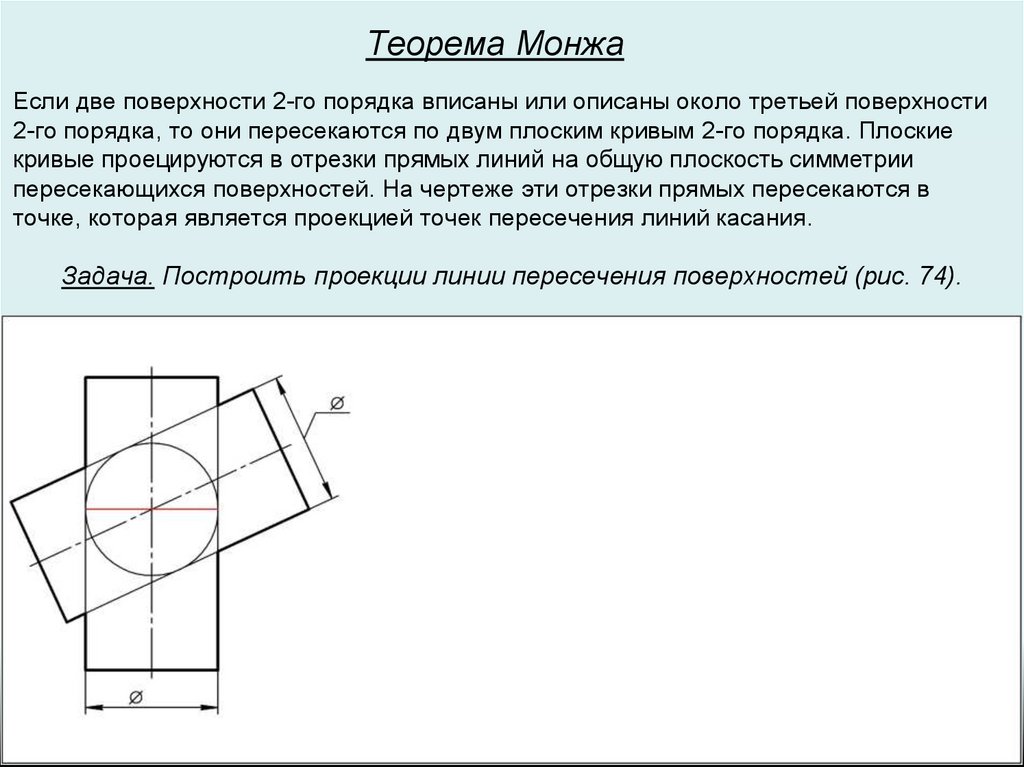
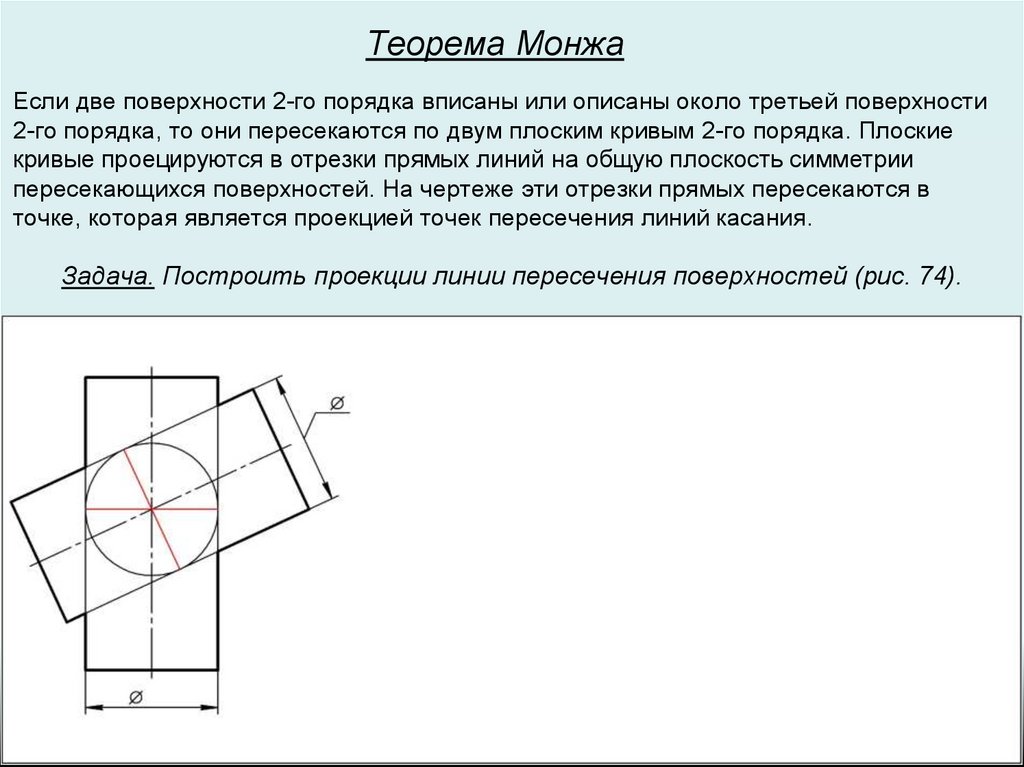
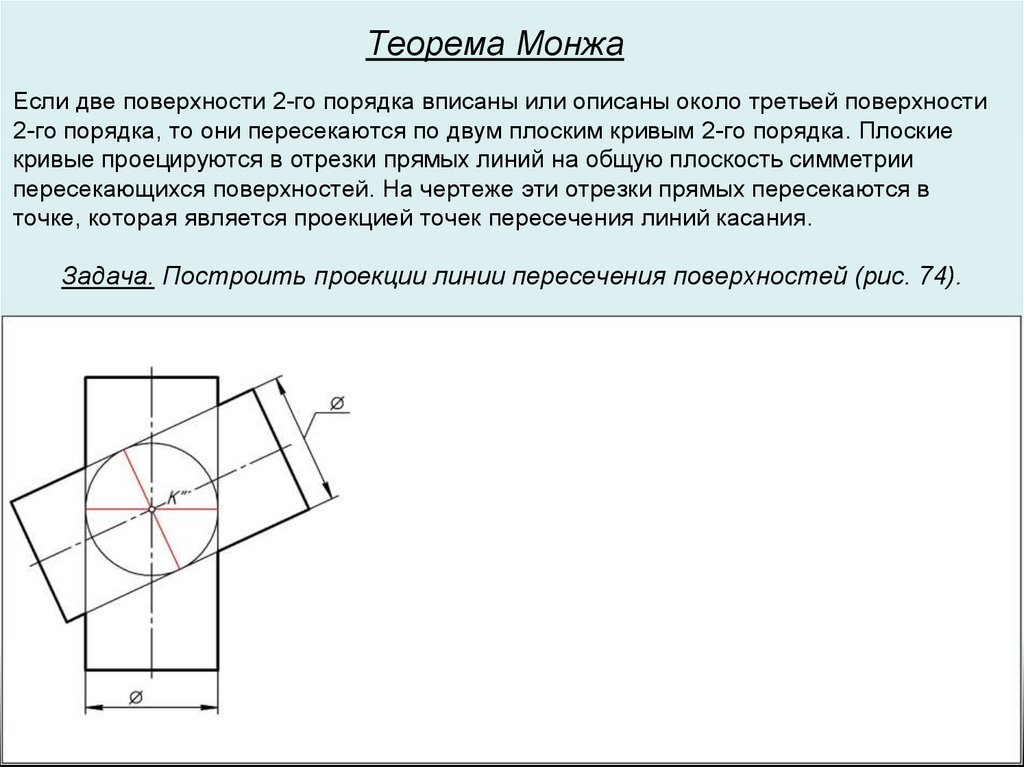
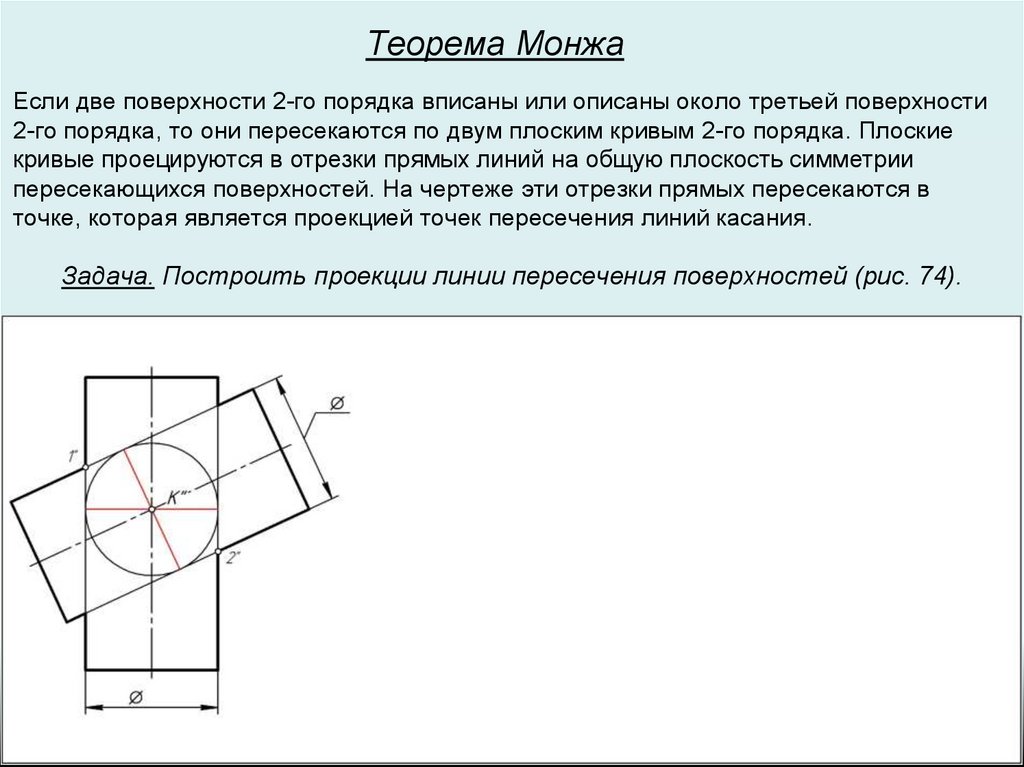
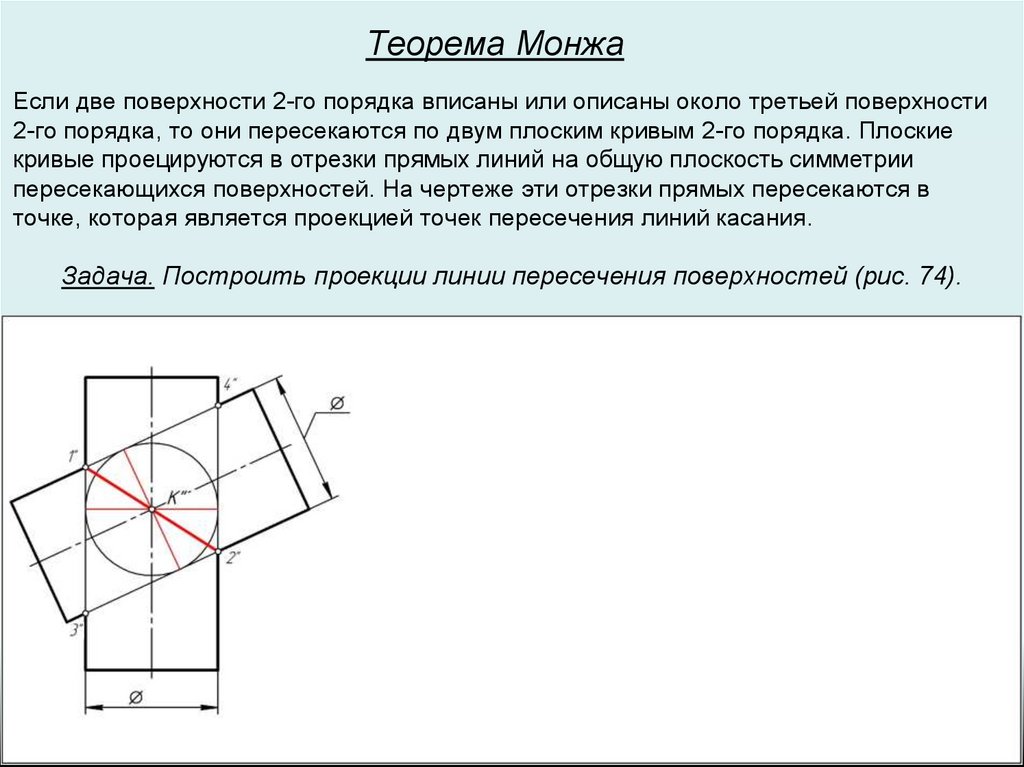
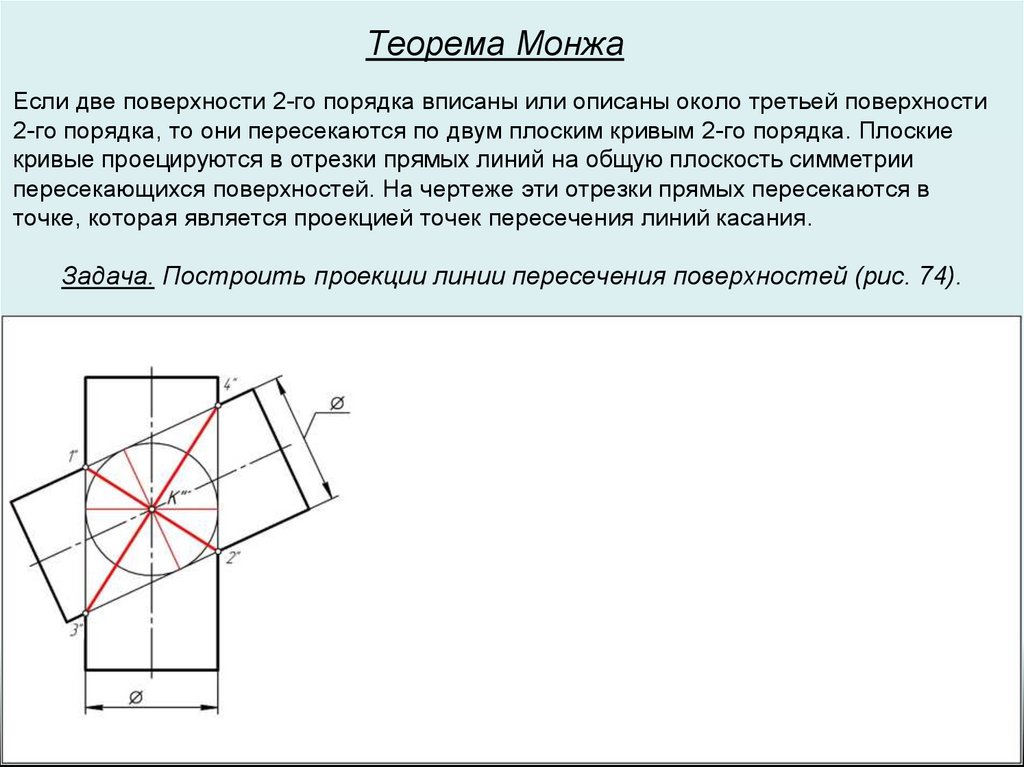
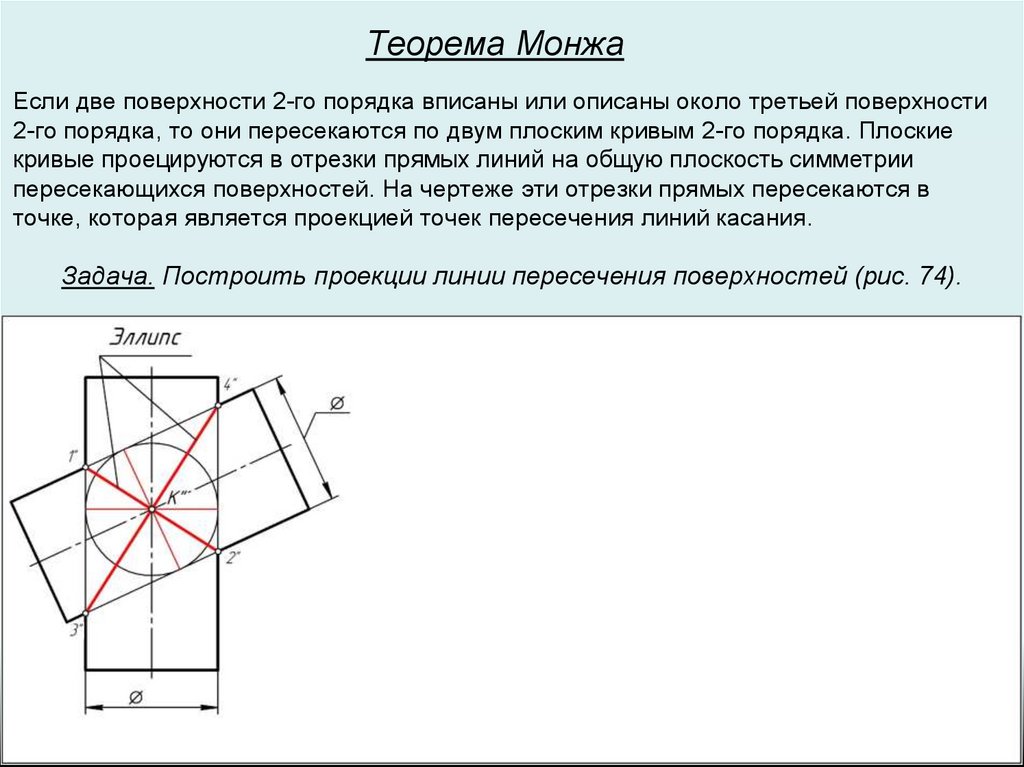
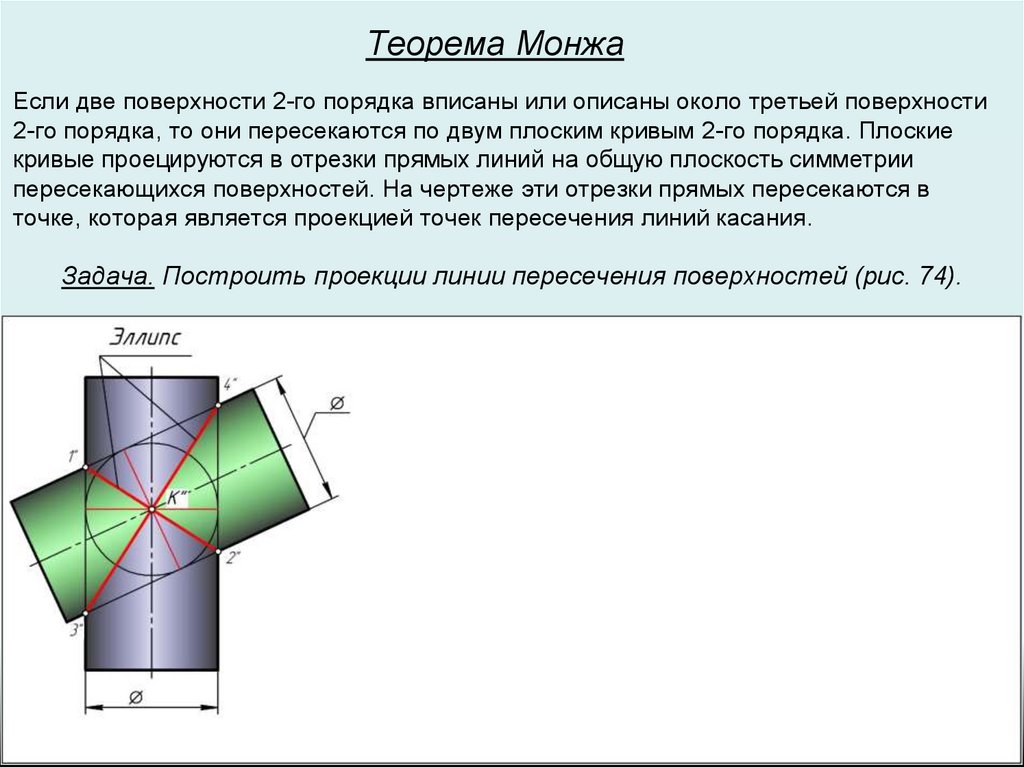
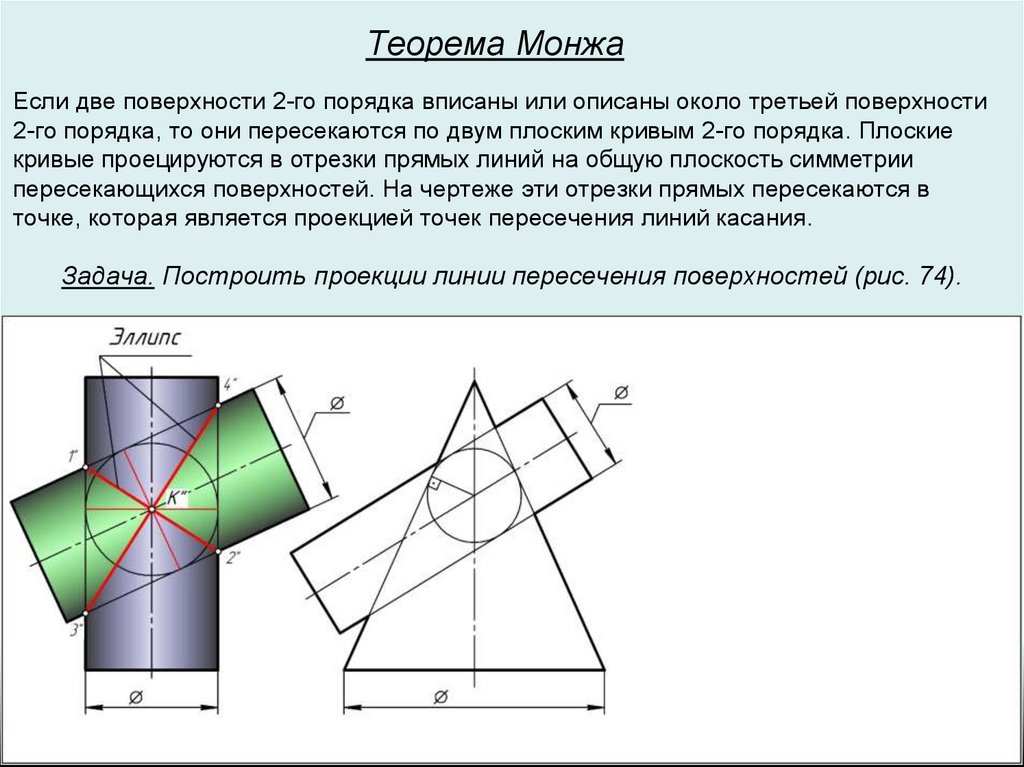
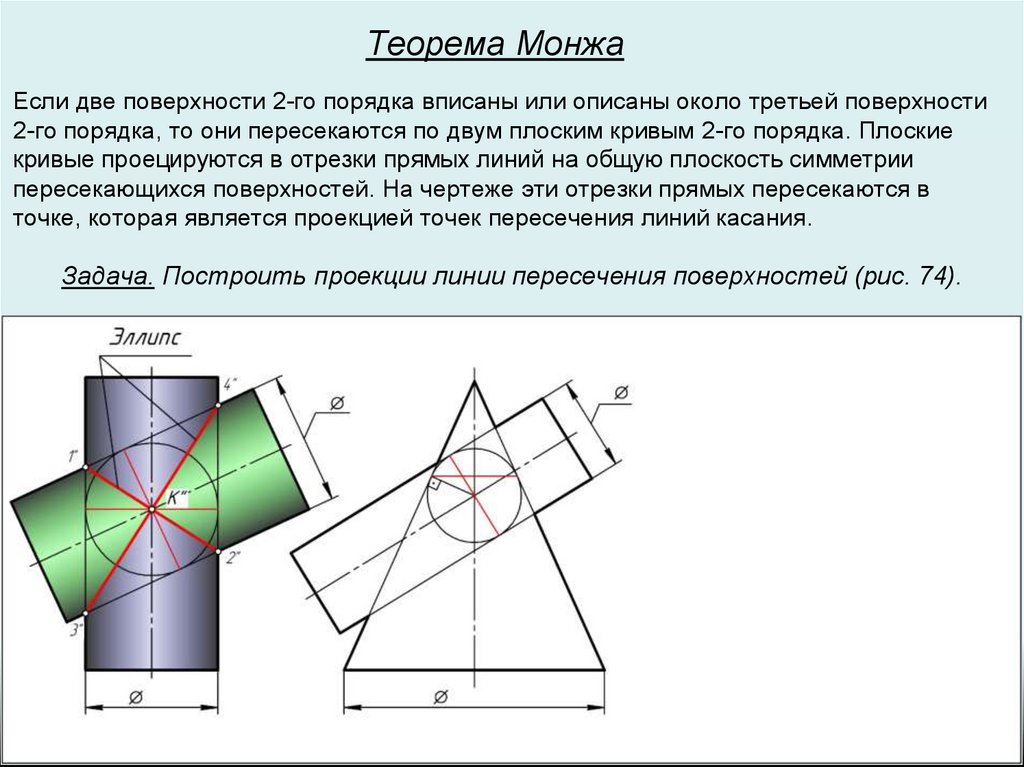
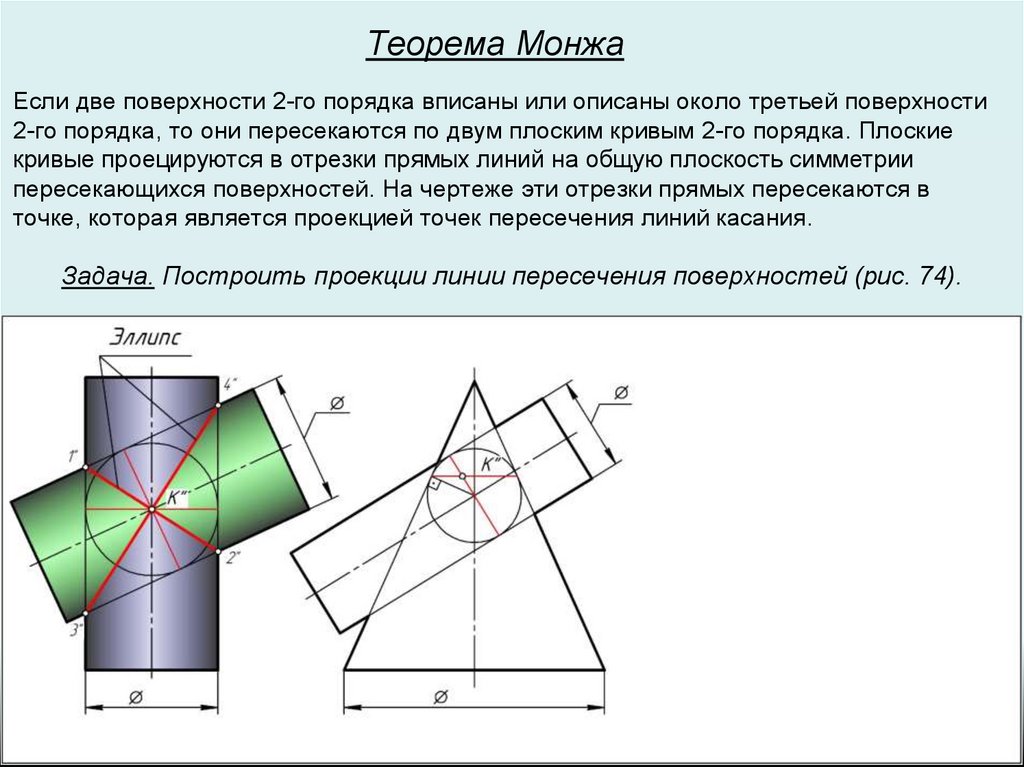
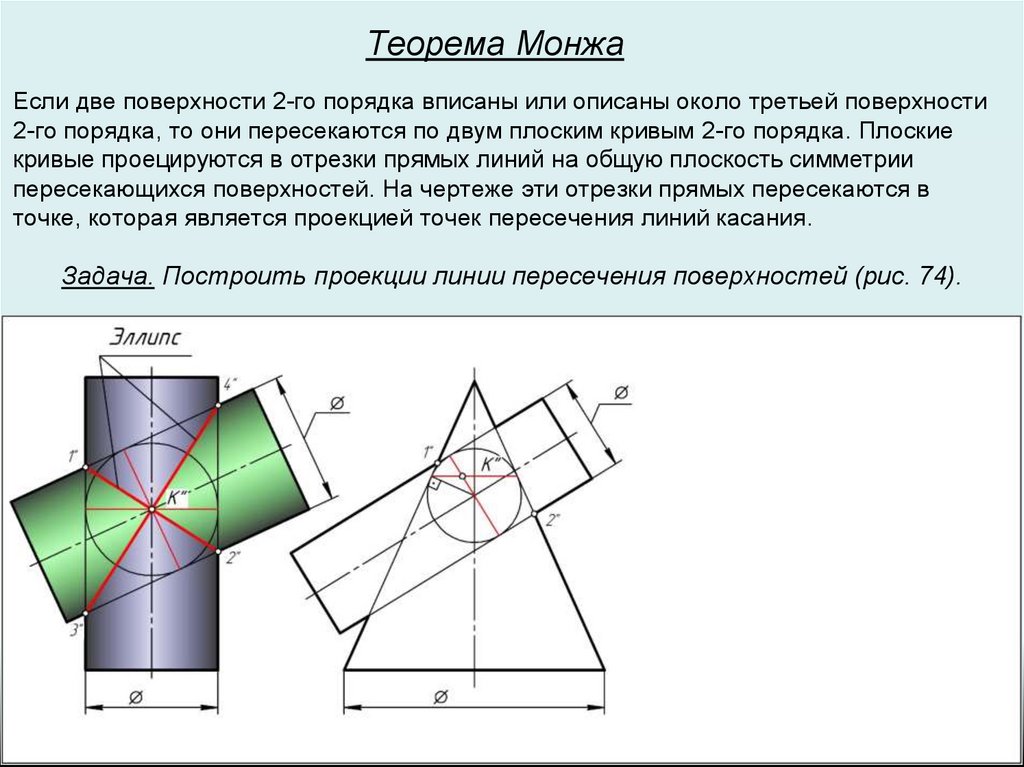
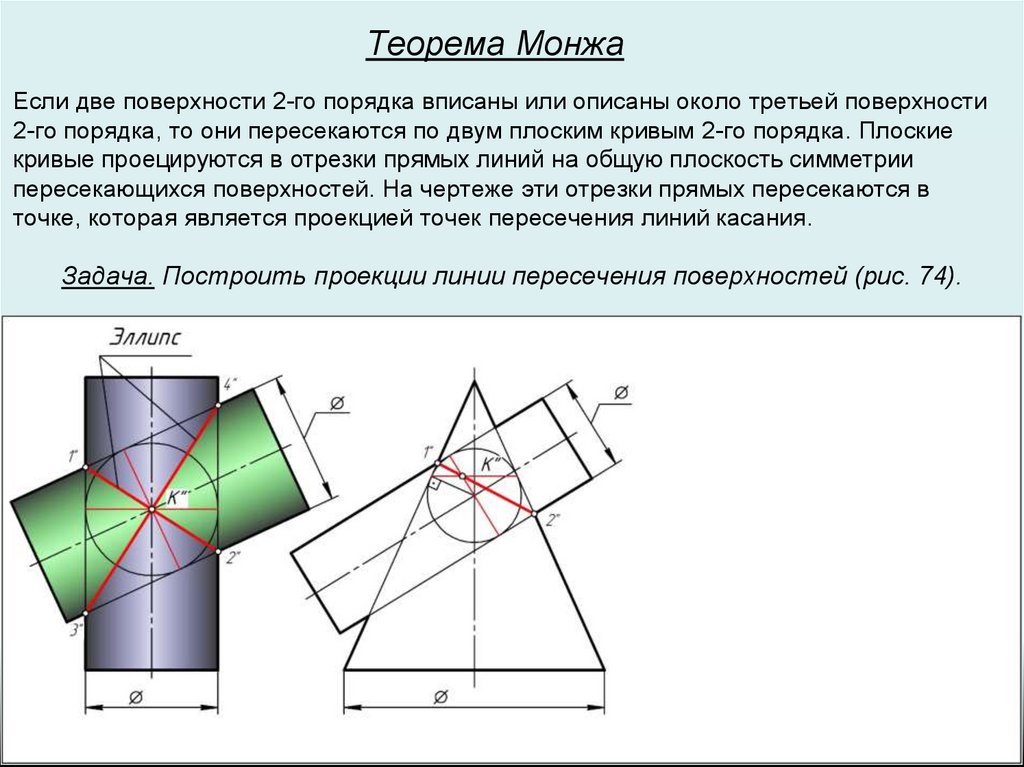
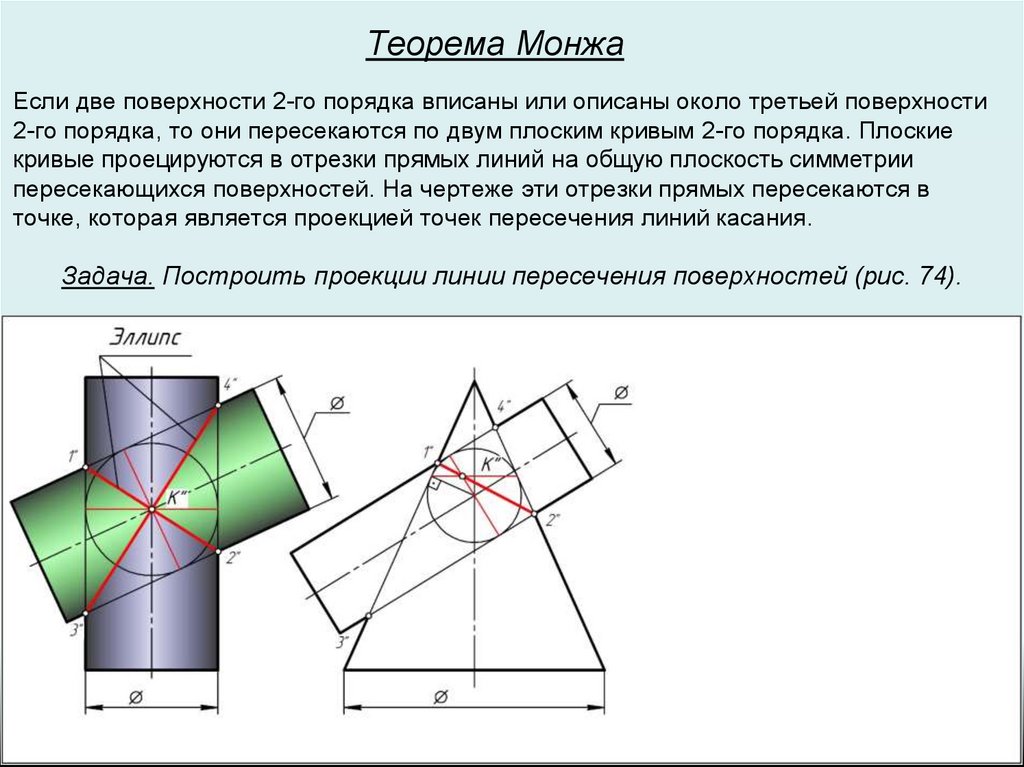
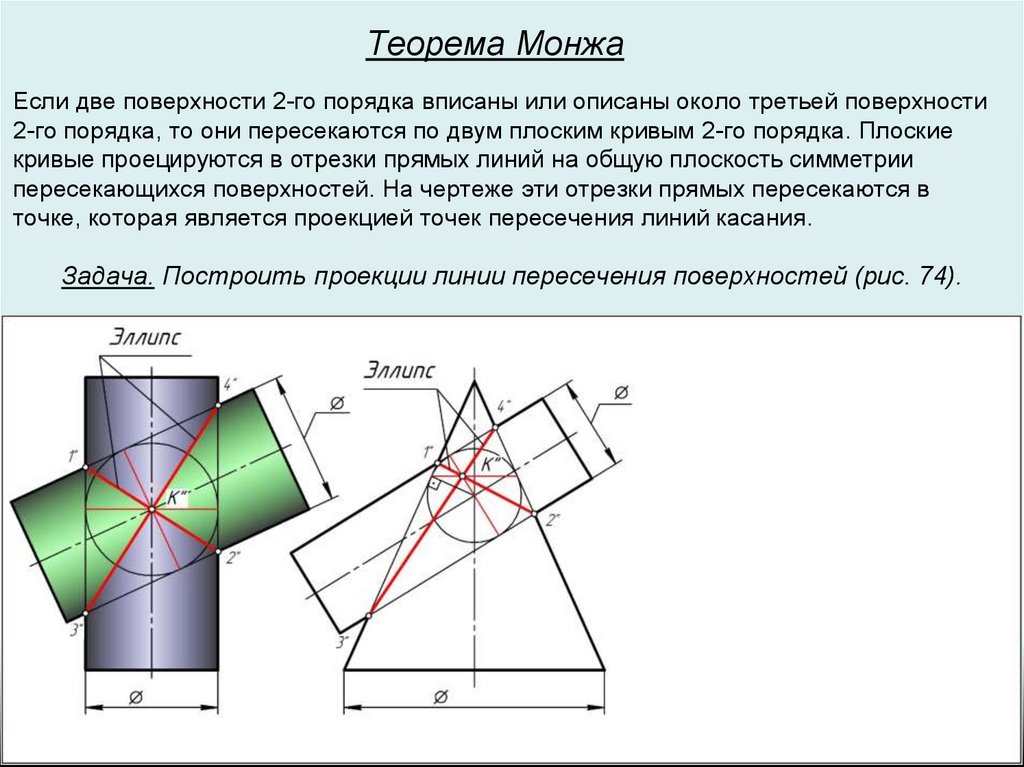
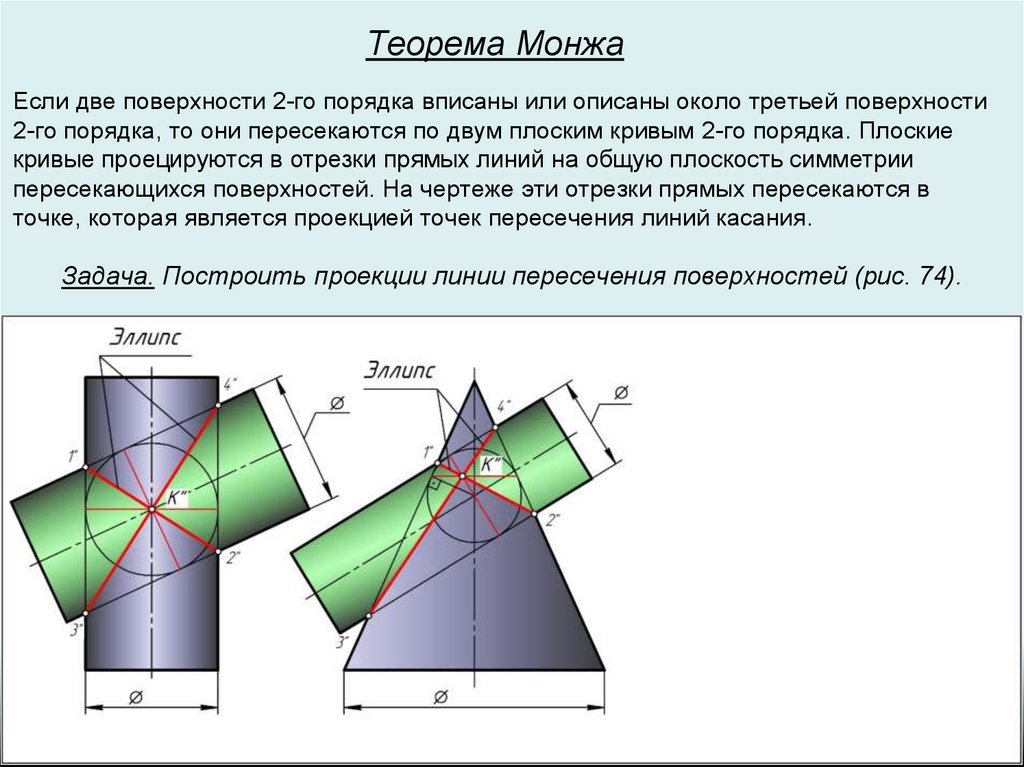
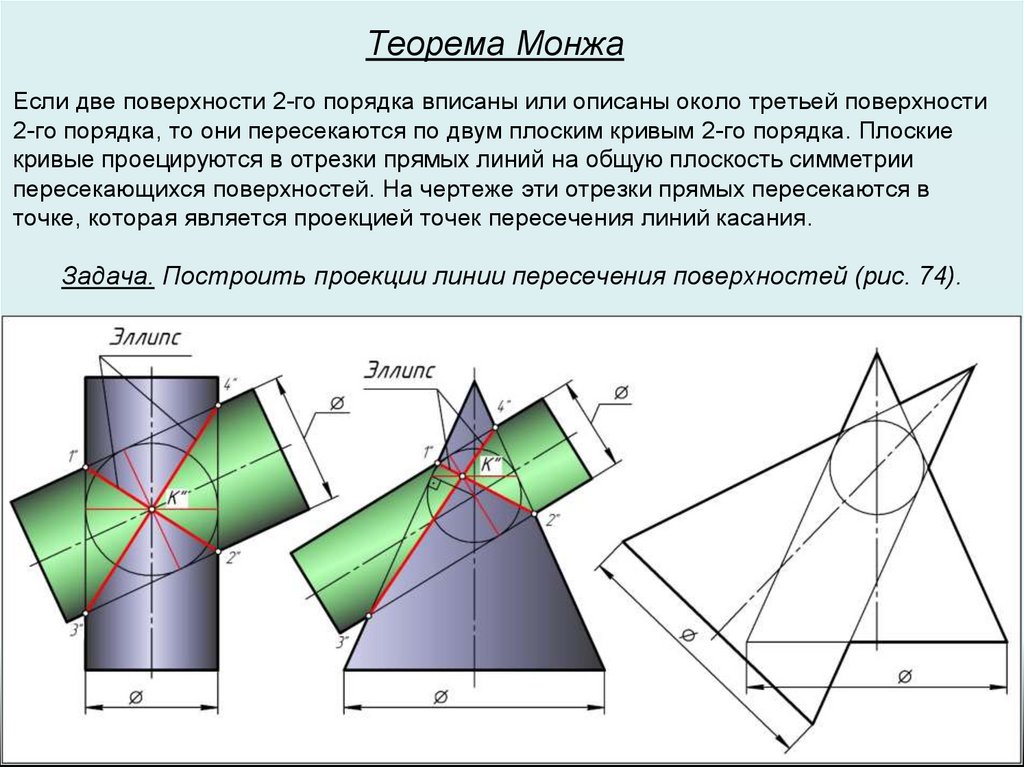
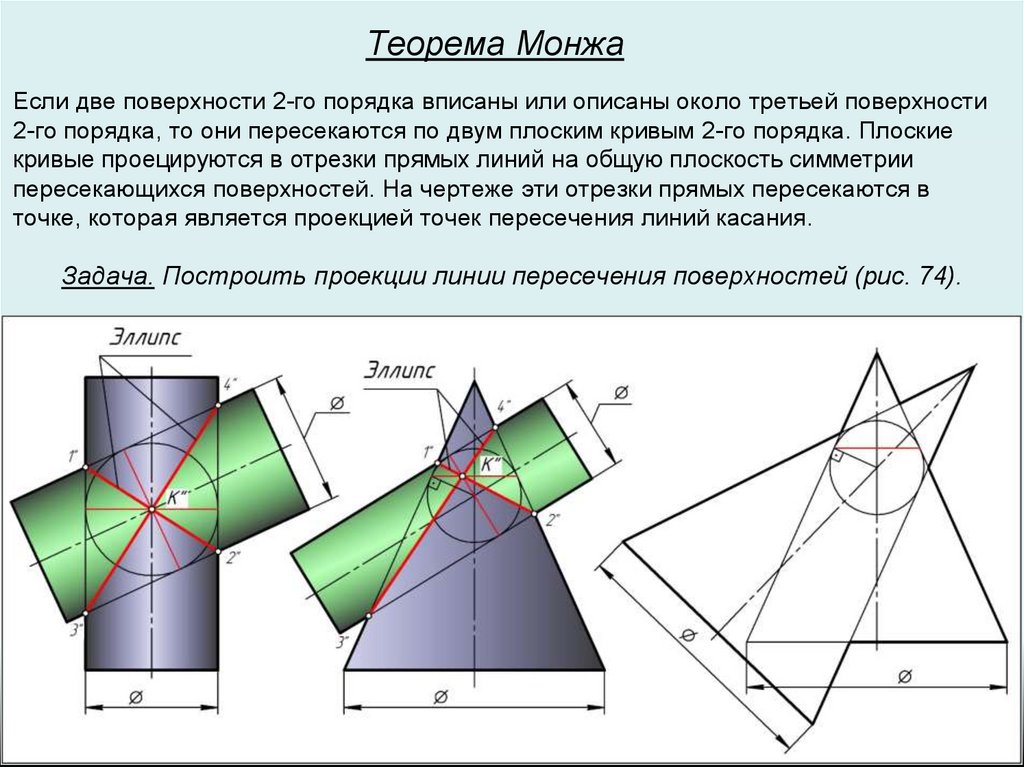
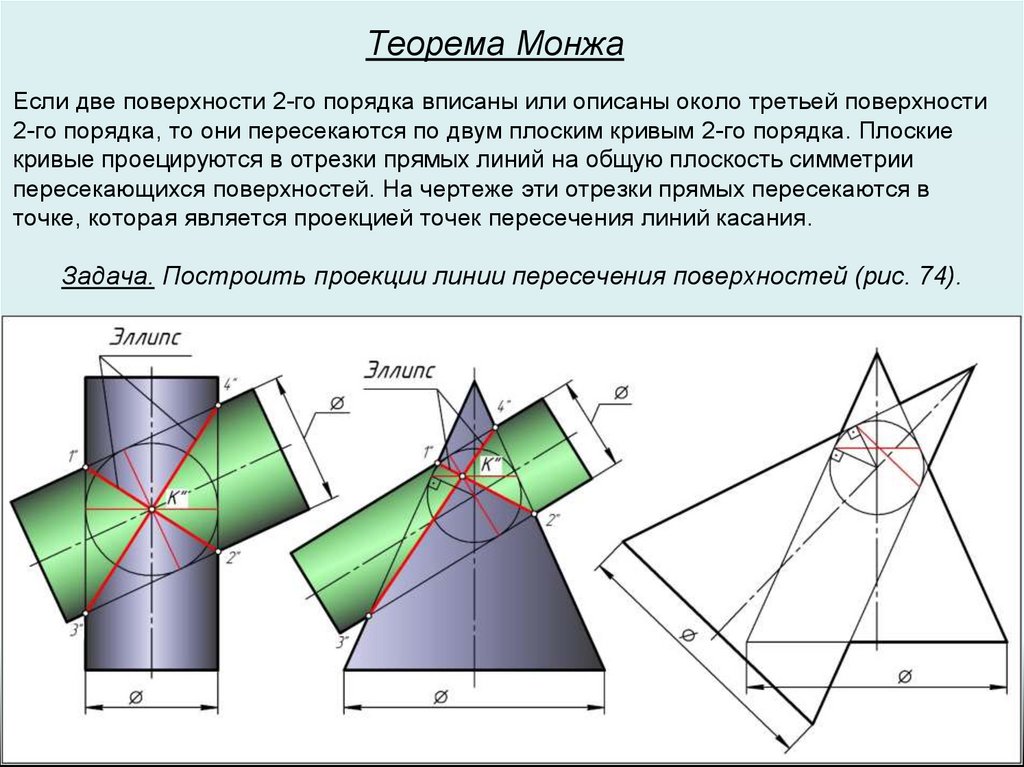
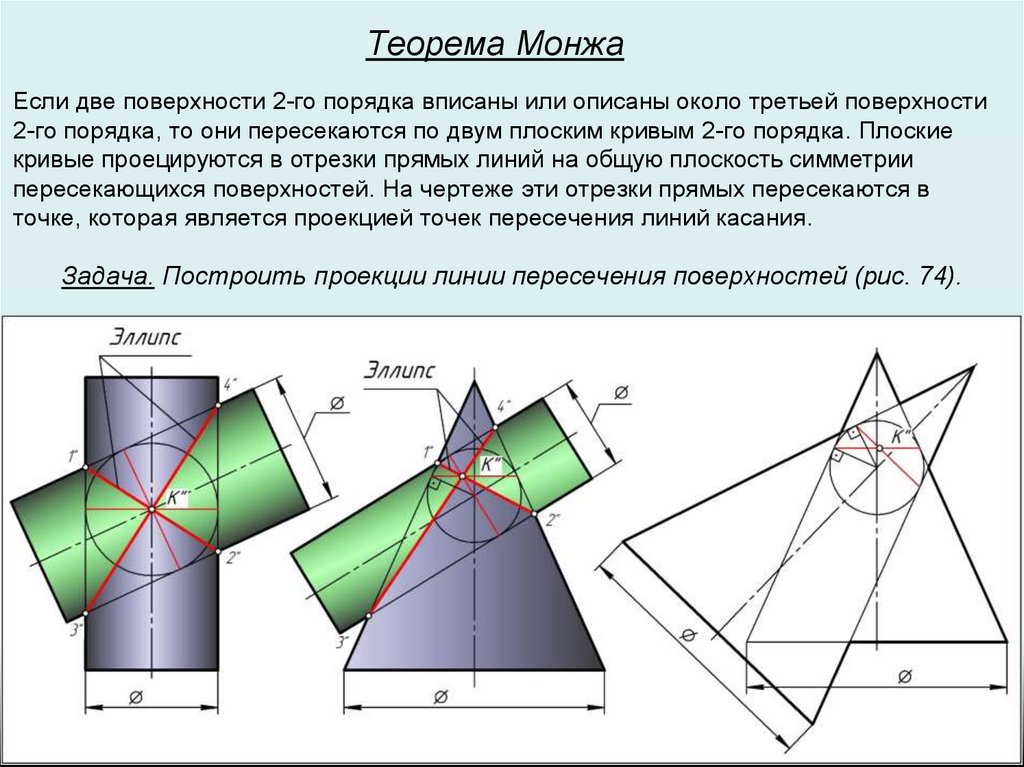
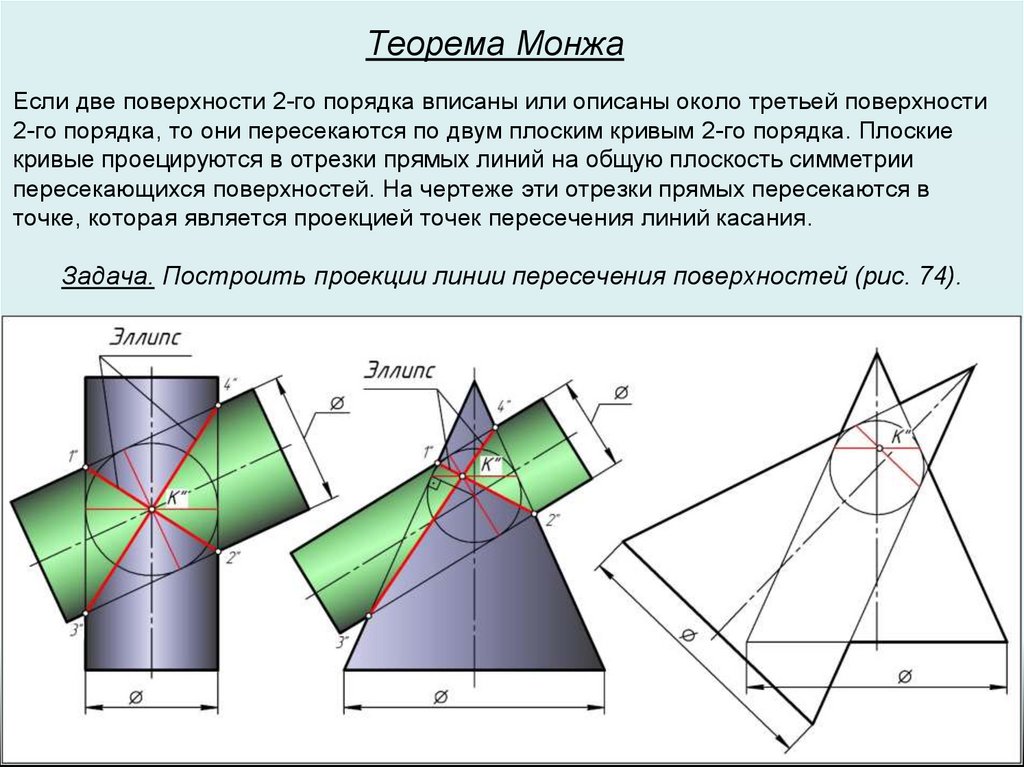
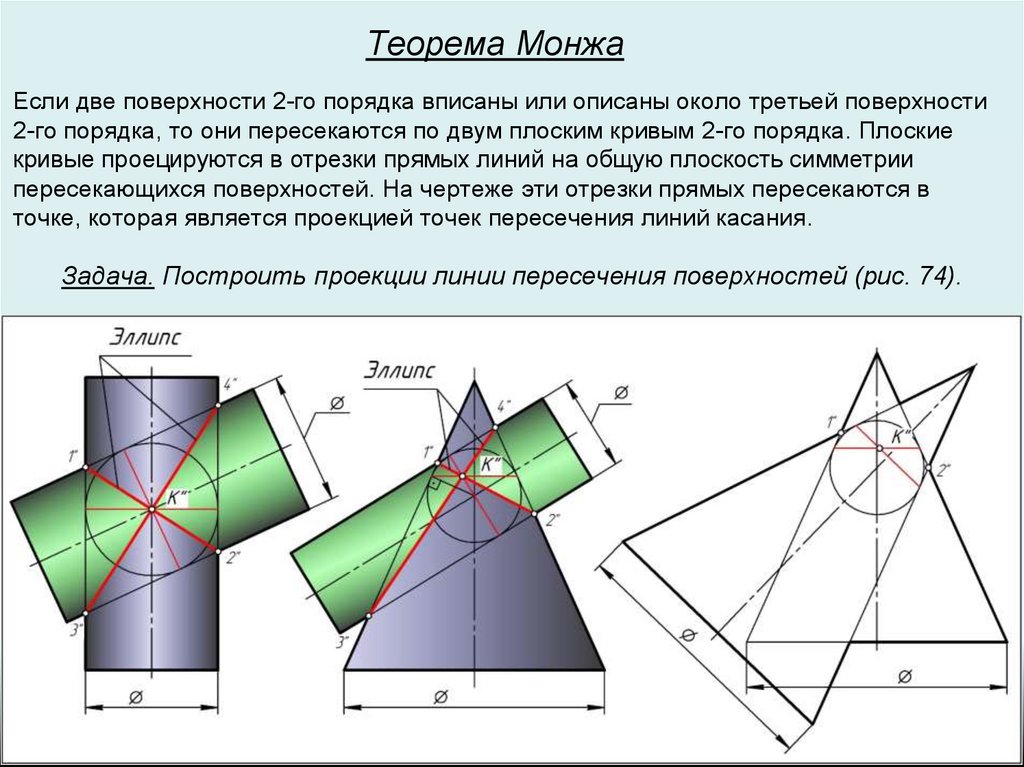
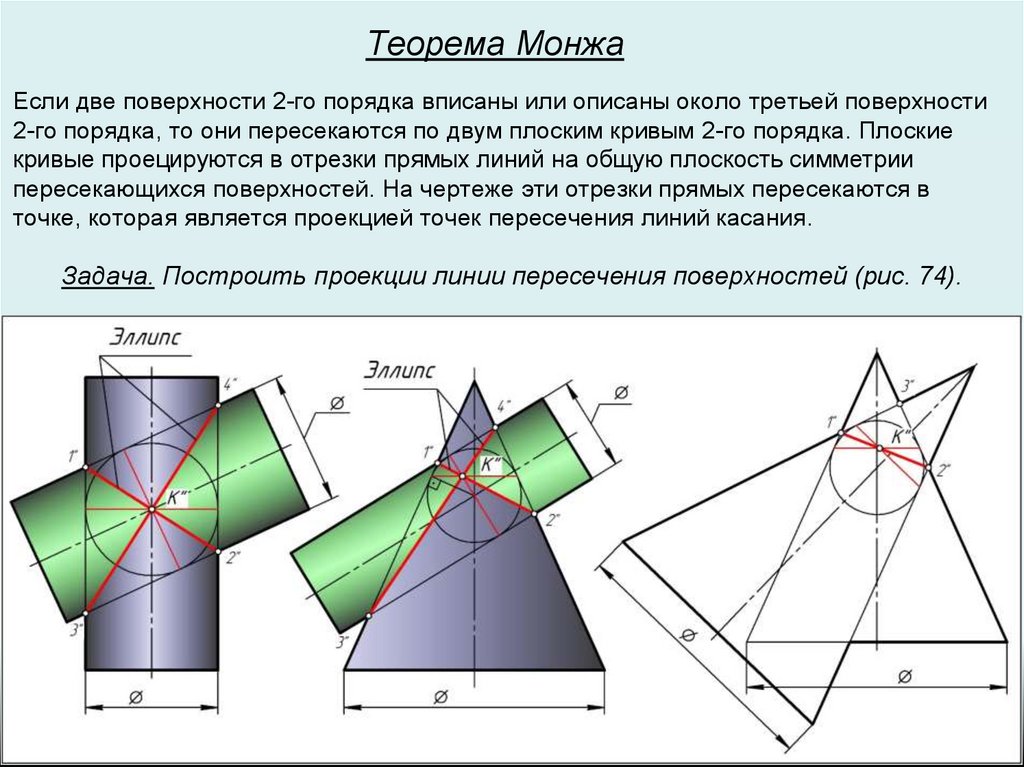
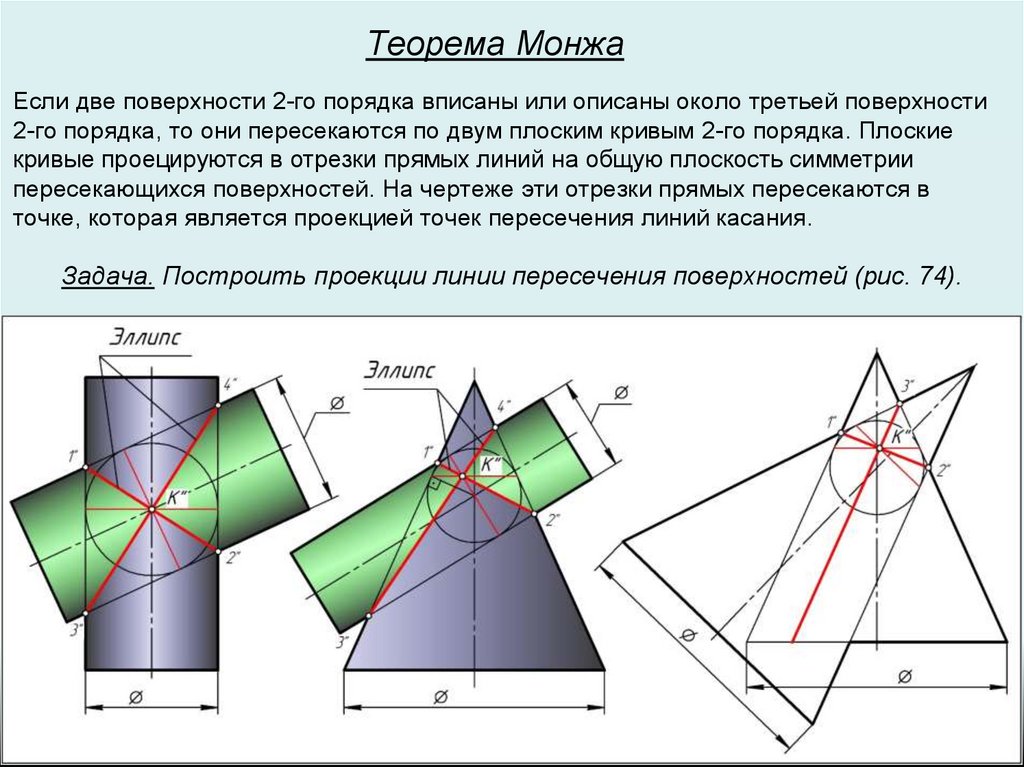
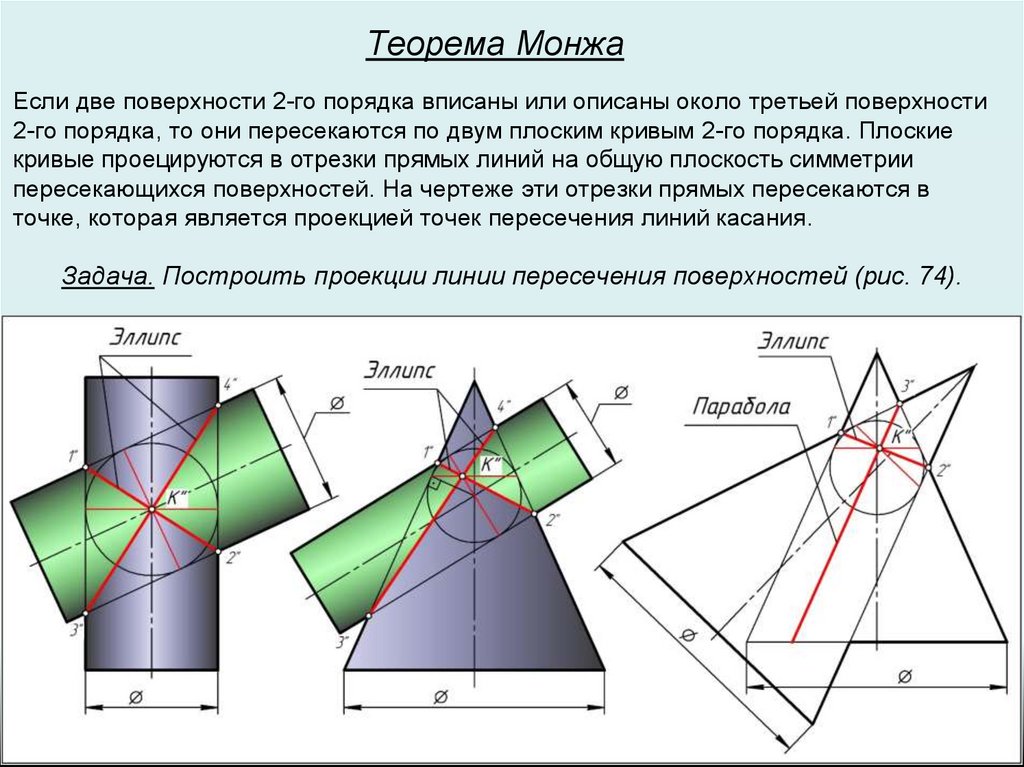
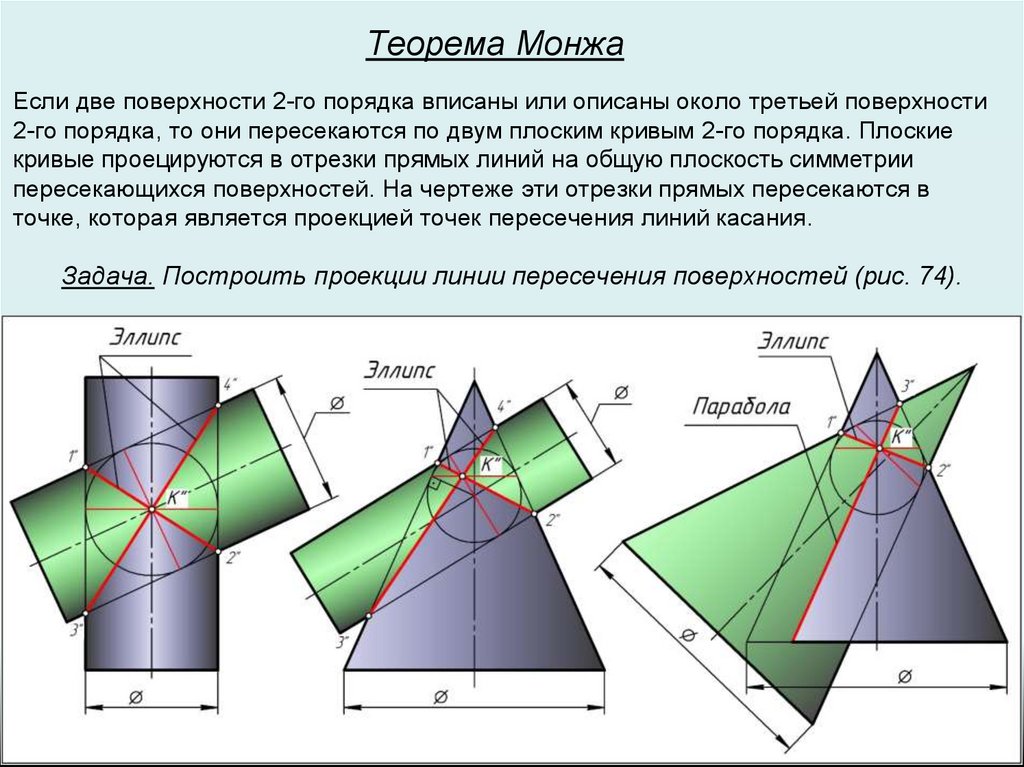
Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

177.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

178.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

179.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

180.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

181.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

182.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

183.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

184.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

185.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

186.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

187.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

188.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

189.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

190.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

191.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

192.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

193.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

194.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

195.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

196.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

197.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

198.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

199.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

200.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

201.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

202.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

203.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

204.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

205.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

206.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).

207.

Теорема Монжа
Если две поверхности 2-го порядка вписаны или описаны около третьей поверхности
2-го порядка, то они пересекаются по двум плоским кривым 2-го порядка. Плоские
кривые проецируются в отрезки прямых линий на общую плоскость симметрии
пересекающихся поверхностей. На чертеже эти отрезки прямых пересекаются в
точке, которая является проекцией точек пересечения линий касания.
Задача. Построить проекции линии пересечения поверхностей (рис. 74).