Показательная и логарифмическая функции

1.

ПОКАЗАТЕЛЬНАЯ И
ЛОГАРИФМИЧЕСКАЯ
ФУНКЦИИ

2.

3.

4.

5.

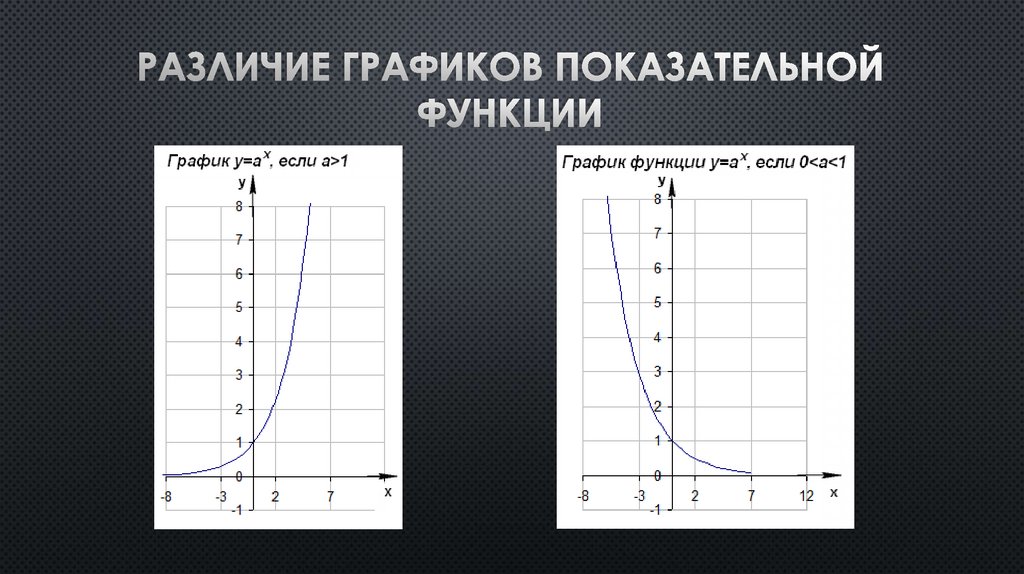
Свойства показательной
функции
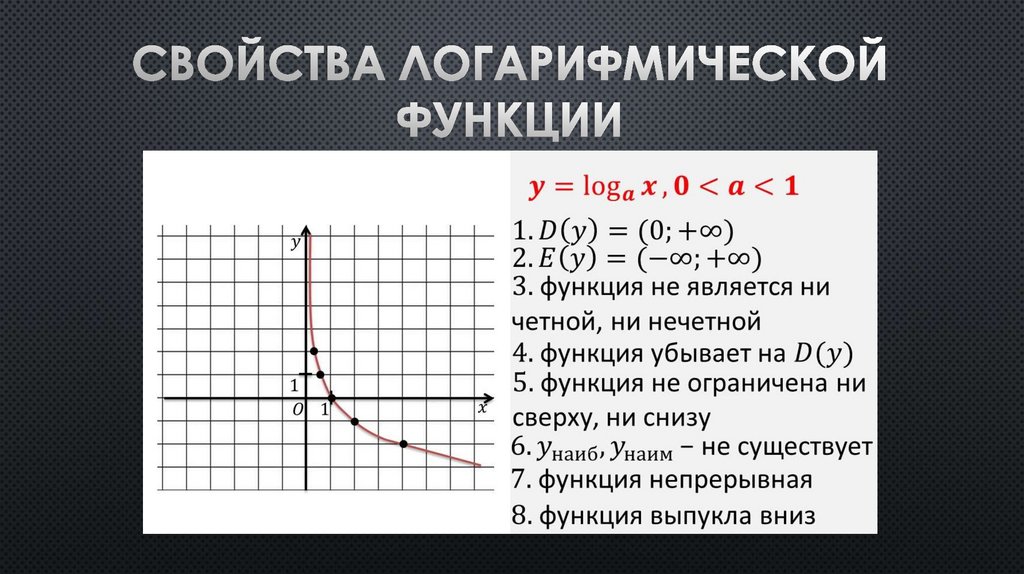
1) Областью определения функции является множество всех действительных чисел
R.
2) Множеством значений функции являются все положительные числа, т.е.
промежуток
3) Наименьшего и наибольшего значений функция не имеет.
4) Функция не является ни нечетной, ни четной. Имеет общий вид.
5) Функция непериодическая.
6) График функции пересекает координатную ось Oy в точке (0; 1).
7) Функция не имеет нулей.
8) При a>1 функция возрастает на всей числовой прямой; при 0<а<1 функция
убывает на множестве R.
9) Функция принимает положительные значения на всей области определения.

6.

7.

8.

9.

10.

Решите уравнение:
3х=4-х
Решение:
На рисунке построены графики
функций у=3х (синим цветом) и у=4-х
(зеленым цветом).
Точка пересечения и будет решением
уравнения: х=1.
Ответ: х=1

11.

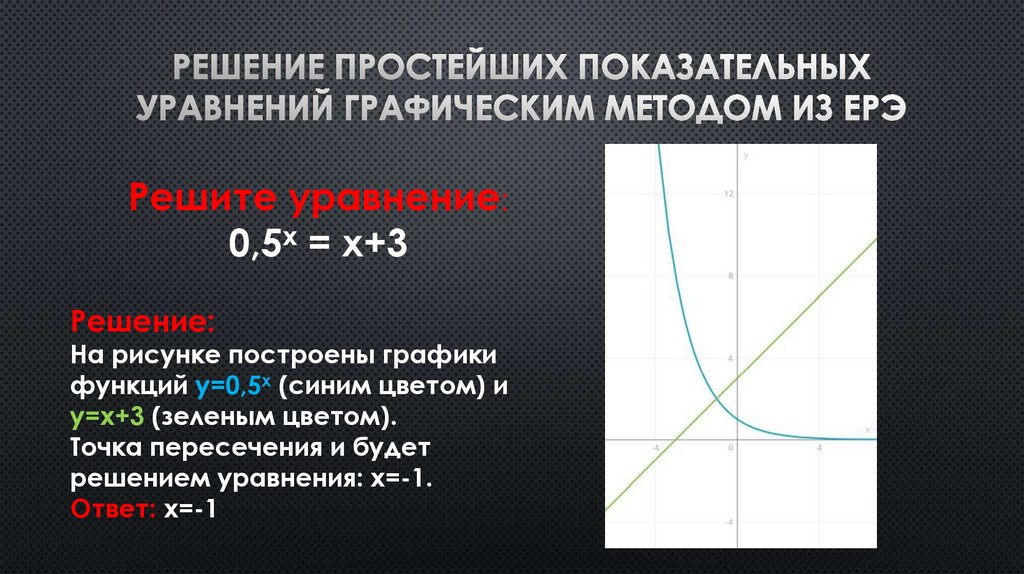
Решите уравнение:
0,5х = х+3
Решение:
На рисунке построены графики
функций у=0,5х (синим цветом) и
у=х+3 (зеленым цветом).
Точка пересечения и будет
решением уравнения: х=-1.
Ответ: х=-1

12.

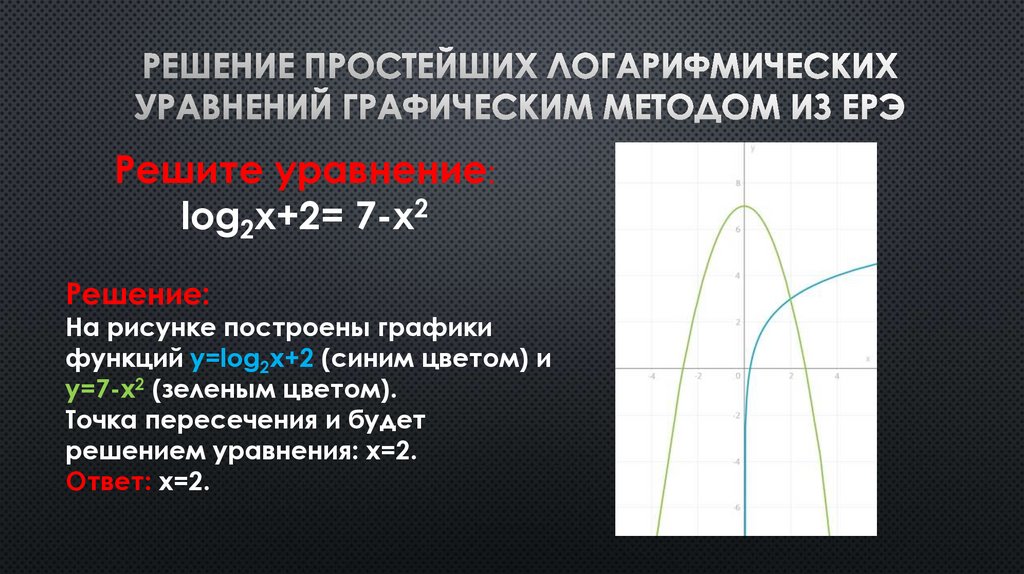
Решите уравнение:
log2x+2= 7-x2
Решение:
На рисунке построены графики
функций у=log2x+2 (синим цветом) и
у=7-x2 (зеленым цветом).
Точка пересечения и будет
решением уравнения: х=2.
Ответ: х=2.

13.

Решите уравнение:
log2(x+1)=-2x+3
Решение:
На рисунке построены графики
функций у=log2(x+1) (синим цветом)
и у=-2x+3 (зеленым цветом).
Точка пересечения и будет
решением уравнения: х=1.
Ответ: х=1.