Similar presentations:
Лекция 3+4. Деревья поиска
1.
Деревья поиска2.
Дерево поискаДерево, дерево с корнем. Высота дерева. Родительские и дочерние узлы,
листья. Количество рёбер
3.
Количество деревьев с пронумерованнымивершинами
Теорема Кэли
Число деревьев на n вершинах, пронумерованных от 1 до n, равно n^(n-2)
Для доказательства воспользуемся кодированием Прюфера для деревьев с
пронумерованными вершинами
4.
Код ПрюфераКодирование производится через последовательное удаление вершин
дерева, имеющих наименьший номер и являющихся концевыми. При этом в
код записывается номер вершины, с которой удаляемая соединена. Когда
остаётся две вершины, формирование кода заканчивается
Чтобы восстановить дерево по коду Прюфера, необходимо выписать код и
множество номеров 0..n. Для каждого шага выбираем очередное число из
кода и минимальное число из i..n, которое не встречается в коде. Построим
ребро и вычеркнем их, а затем повторим процесс, пока не останется два
незадействованных числа. Проведём между ними ребро
5.
Код ПрюфераЛюбое дерево естественно переводится в Код Прюфера. Код имеет размер
(n-2), всего кодов на n вершинах можно построить n^(n-2). Отсюда и
получается оценка на количество пронумерованных деревьев
6.
Обход в глубинуДля бинарных деревьев -- pre-, post- и in-order
7.
Обход в ширину8.
Деревья поискаПоиск ключа, вставка, удаление
Необходимость балансировки
9.
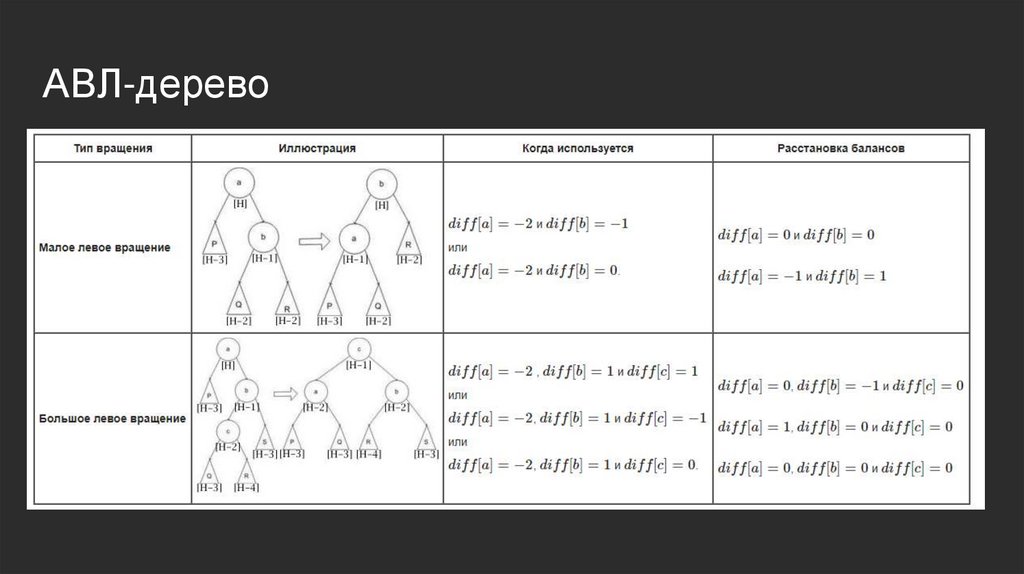
АВЛ-деревоХотим поддерживать разницу между поддеревьями любой вершины |h(L)h(R)| <= 1
Для этого в процессе проведения операций будем использовать вращения
двух типов:
10.
АВЛ-дерево11.
АВЛ-деревоДобавление элемента: сначала идём вниз от корня как при поиске, пока не
дойдём до отсутствующей вершины. Вставляем элемент и поднимаемся
вверх.
Если поднялись из левого поддерева -- diff увеличивается на 1, если из
правого -- уменьшается. Встретив ситуацию |h(L)-h(R)| > 1, совершаем
необходимые повороты. Если после вращения diff стал равен 0,
останавливаемся, иначе -- продолжаем подъём
12.
АВЛ-деревоУдаление вершины.
Если вершина -- лист, то просто удаляем. Если внутренняя, то найдём
ближайшую по значению вершину, поменяем их местами и удалим. Далее
поднимаемся из удалённой вершины и восстанавливаем баланс
13.
Слияние двух АВЛ-деревьевПусть есть деревья X и Y, все ключи X <= любому ключу Y.
Пусть высота X меньше, чем у Y. Тогда удаляем у X самую правую вершину
(b), а у Y спускаемся вниз влево, пока не дойдём до вершины, имеющей
высоту как у X (c) . Делаем подвешиваем b вместо c, c делаем его правым
поддеревом, а X -- левым. Поднимаемся наверх и балансируем дерево
поворотами
14.
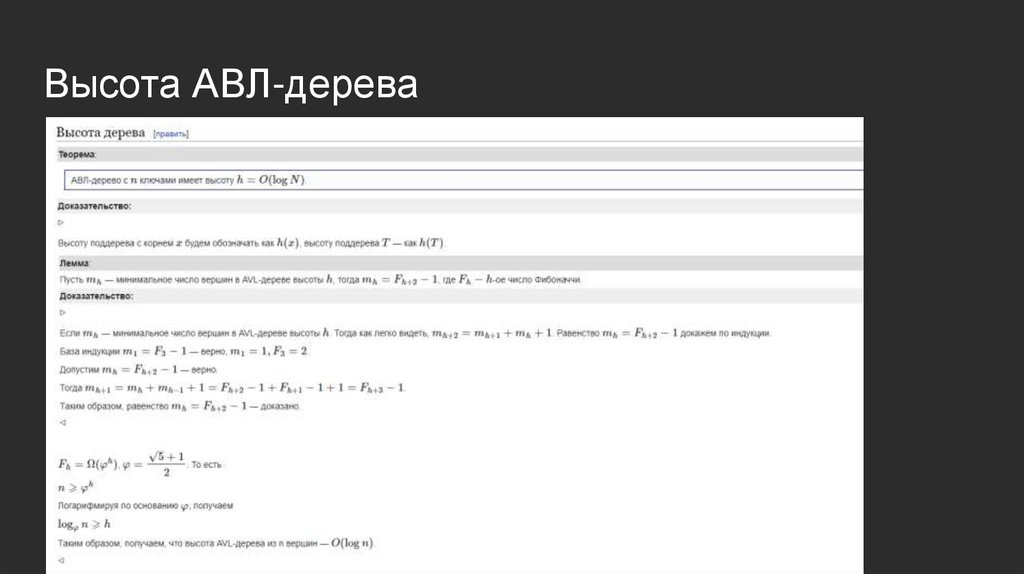
Высота АВЛ-дерева15.
Сплей-деревоДерево, позволяющее получать быстрый доступ к элементам, которые были
использованы последними
16.
ЭвристикиmoveToRoot(x) -- совершает повороты (x,p), где х -- вершина, p -- её предок,
пока x не станет корнем дерева
splay(x) -- чередует 3 разновидности поворотов
zig(x) = (x,p) -- если p -- корень
zig-zig(x) = (p,q) + (x,p) -- если x и p -- правые либо левые дети
zig-zag(x) = (x,p) + (x,q) -- если х и р -- разные дети
17.
Операции над сплей-деревомmerge -- запускаем splay от самого большого элемента X, подвешиваем
справа Y ( Х <= Y)
split(x) -- запускаем splay(x), возвращаем левое и правое поддерево x
add(x) -- запускаем split(x), подвешиваем левое и правое поддерево к x в
зависимости от того, больше или меньше корень, чем x
remove(x) -- запускаем splay(x), возвращаем merge его поддеревьев
18.
19.
Декартово дерево поиска-- хранит элементы (x,y), где x -- ключ, а y -- приоритет. Декартово дерево
является деревом поиска по ключу и кучей по приоритету
20.
Операции над декартовым деревомsplit(x): пусть x больше корня, тогда в левом дереве окажется левое
поддерево и левый результат операции split над правым поддеревом
Сложность -- высота дерева
merge(T1,T2) (все x1 < x2): Пусть у T1 корень больше по y. Тогда его левое
поддерево -- левое поддерево результата, а правое поддерево результата -слияние его правого поддерева и T2
21.
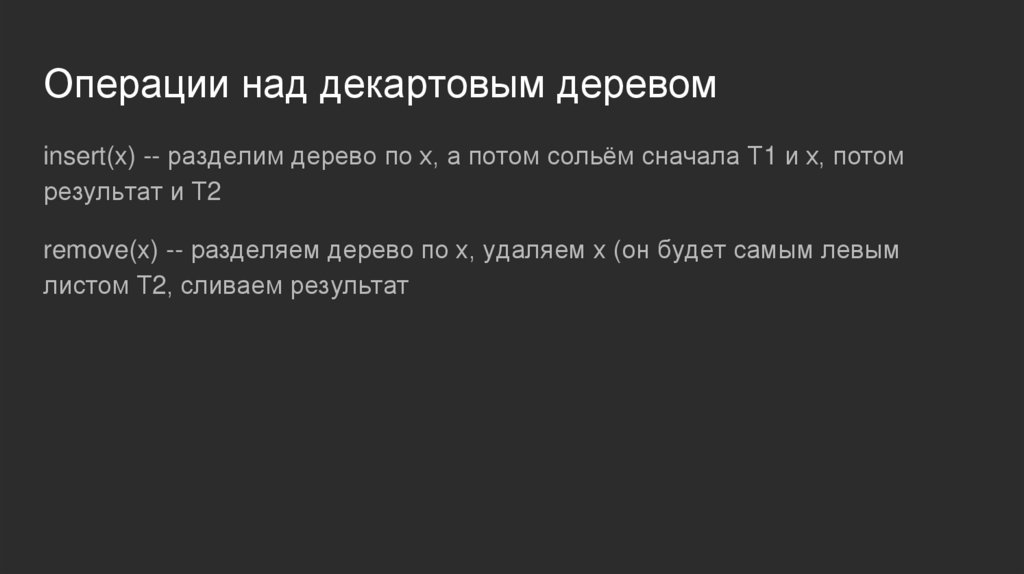
Операции над декартовым деревомinsert(x) -- разделим дерево по x, а потом сольём сначала T1 и x, потом
результат и T2
remove(x) -- разделяем дерево по х, удаляем x (он будет самым левым
листом T2, сливаем результат
22.
Построение1. По очереди вставим все элементы
2. Пусть элементы отсортированы по возрастанию ключей. Смотрим на
самый правый элемент в уже построенном дереве. Если можем -добавляем. Если нет -- поднимаемся наверх до тех пор, пока не
встретим больший приоритет. Тогда подвешиваем поддерево с
меньшим приоритетом слева к вставляемому элементу, а сами
становимся на его место.
Всего к каждому элементу обратимся не более двух раз (если мы
пробежали его, когда шли наверх -- больше не встретим). Итого
асимптотика построения O(n)
23.
Высота декартова дереваТеорема. В декартовом дереве на n узлов, у которого приоритеты -равномерно распределённые случайные величины, средняя глубина
вершины -- O(logn)
24.
Красно-чёрное деревоДерево поиска, вершины которого промаркированы определённым цветом:
красным или чёрным
1.
2.
3.
4.
Каждая вершина — либо красная, либо черная
Каждый лист — черный
Если вершина красная, оба ее ребенка черные
Все пути, идущие от корня к листьям, содержат одинаковое количество
черных вершин
25.
Высота красно-чёрного дереваЧёрная высота x -- количество чёрных вершин на пути из х в лист
Лемма. В КЧ-дереве с чёрной высотой Hb количество внутренних вершин не
менее 2^(Hb-1)-1.
Докажем по индукции. Если одна чёрная вершина, то Hb=1. 2^(1-1)-1 = 0
Любая внутренняя вершина x имеет двух потомков -- их высоты на 1 меньше
высоты x. Чёрные высоты потомков -- либо hb(x), либо hb(x)-1. Значит, в
каждом из них не меньше 2^(hb(x)-2)-1 вершин. Суммарно + 1 за x -2*(2^hb(x)-2 - 1) + 1 = 2^(hb(x)-1)-1 вершин, чтд
26.
Высота красно-чёрного дереваЛемма. Высота красно-чёрного дерева с N вершинами равна O(logn)
Количество красных вершин не более h/2, чёрным -- не менее h/2-1
N>=2^(h/2 - 1)-1
log(N+1)>=h/2-1
h<=2(log(N+1)+1) => h = O(logn)
27.
Вставка элементаИдём от корня до листа по условиям деревья поиска.
Вставляем вершину с красным цветом. Если отец чёрный -- ничего не
нарушено. Если отец красный -- смотрим на дядю:
Дядя красный -- перекрашиваем отца и дядю в чёрный, деда в красный,
балансируем дальше.
Дядя чёрный -- выполняем поворот между отцом и дедом, перекрашиваем
обоих
28.
Удаление элементаТри варианта:
Мы в листе -- изменяем указатель родителя на nul
Есть один ребёнок -- вешаем его вместо вершины
Два ребёнка -- ищем вершину со следующим значением (самая левая в
правом поддереве), копируем его в нашу вершину и удаляем одним из
способов выше
Если удаляемая вершина была красной -- балансировка не нужна
Если чёрной, есть несколько случаев:


























 programming
programming








