Как банки создают деньги

1. Как банки создают деньги

Интегрированный урок по математике и
экономике «Геометрическая прогрессия и
её приложения в экономике».
Как банки создают
деньги
Габрусь Н.Ю. Клочкова Т.Н.
МКОУ «Шайковская СОШ №2»
Кировского района Калужской
области

2. Когда появились первые банки

Так выглядел великий г.Вавилон – место,
где сформировались первые настоящие
крупные банки.
Древняя Греция Храм
Аполлона на о. Делос.

3. История российских банков

Анна Ивановна (Иоанновна)
— российская императрица
(1730-1740).
Елизавета Петровна (1709-1761/62),
российская императрица с 1741,
дочь Петра I.

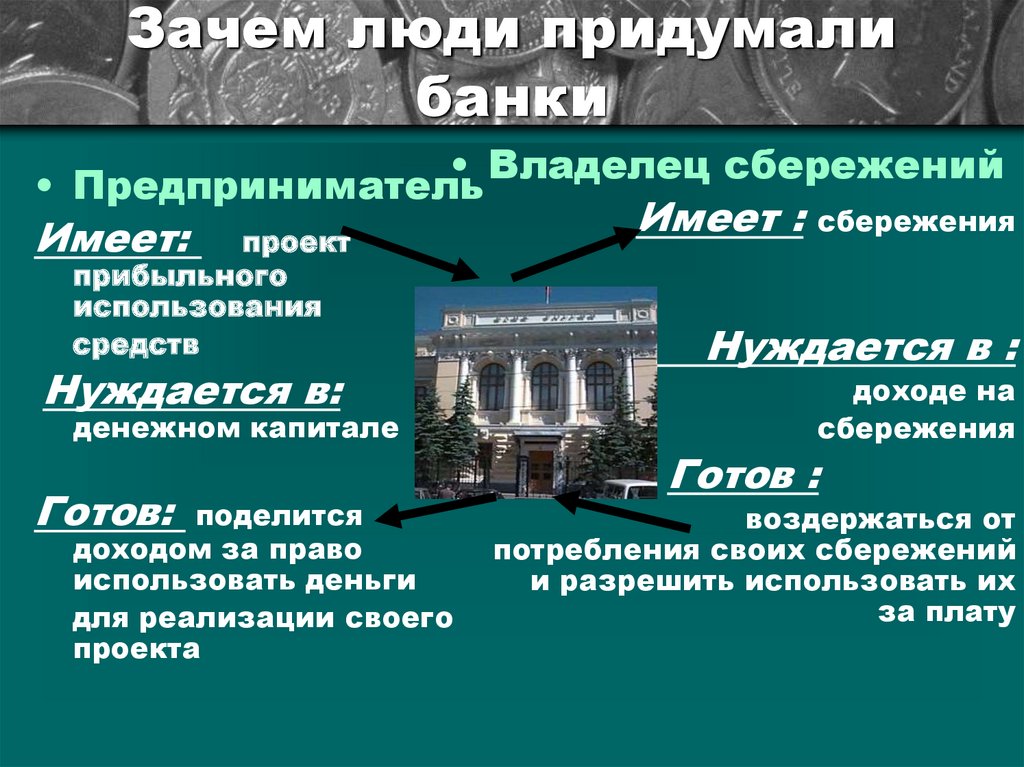
4. Зачем люди придумали банки

• Владелец сбережений
• Предприниматель
Имеет:
проект
прибыльного
использования
средств
Нуждается в:
денежном капитале
Готов:
поделится
доходом за право
использовать деньги
для реализации своего
проекта
Имеет :
сбережения
Нуждается в :
доходе на
сбережения
Готов :
воздержаться от
потребления своих сбережений
и разрешить использовать их
за плату

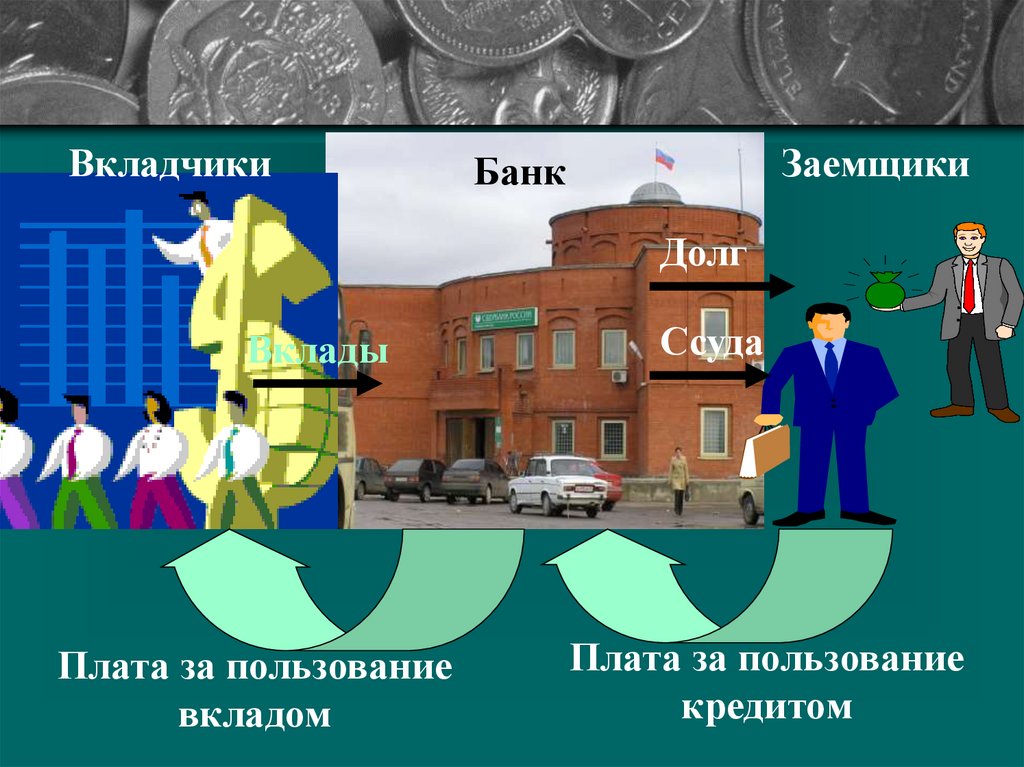
5.

Вкладчики
Заемщики
Банк
Долг
Вклады
Плата за пользование
вкладом
Ссуда
Плата за пользование
кредитом

6. Цели:

Каким образом приобретенные
знания по математике, могут быть
сразу использованы для решения
важных задач современной экономики
Формирование умения, пользуясь
формулой суммы конечного числа
первых членов геометрической
прогрессии, находить суммарный
объем кредитов.
Выяснить, в чем суть кредитной
эмиссии, другими словами, каким
образом банки могут увеличивать
количество денег в экономике.

7. Вспомним основные определения.

• Определение
геометрической
прогрессии
• Формула общего
члена
геометрической
прогрессии:
a n a1q
•Сумма первых n
членов
геометрической
прогрессии:
a1 (1 q n )
Sn
1 q
n 1
•Бесконечно
убывающая
геометрическая
прогрессия. Смысл её
суммы:
a1
S
1 q

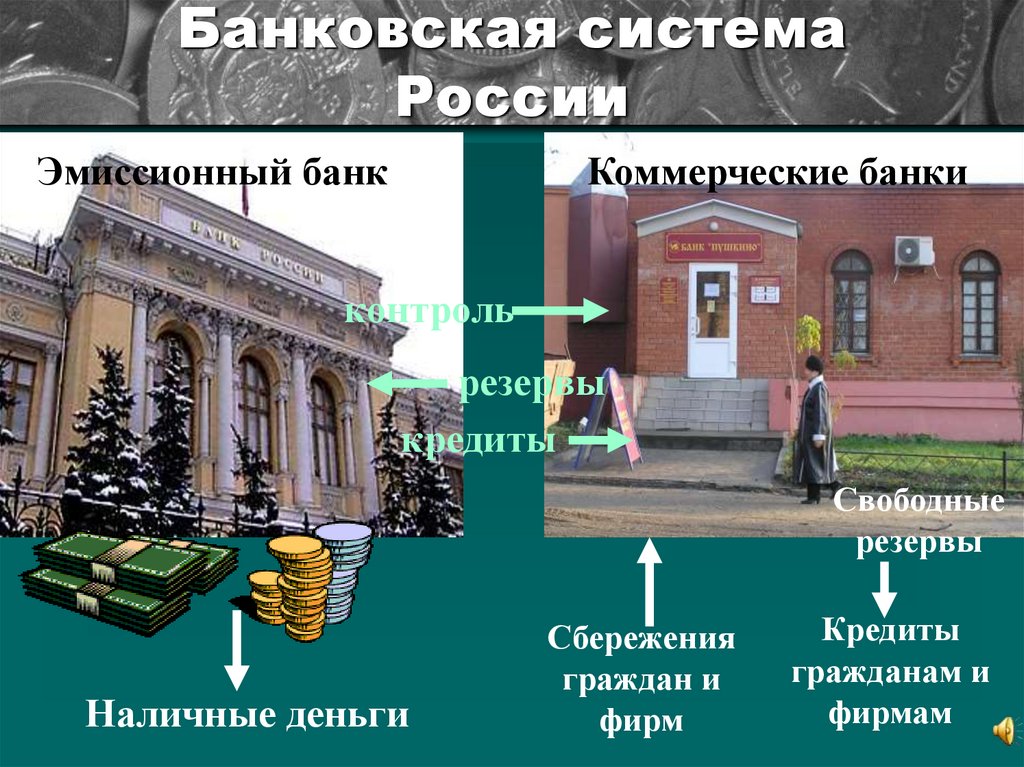
8. Банковская система России

Эмиссионный банк
Коммерческие банки
контроль
резервы
кредиты
Свободные
резервы
Наличные деньги
Сбережения
граждан и
фирм
Кредиты
гражданам и
фирмам

9. Представителям банков - предлагается найти обязательные и свободные резервы своих банков с учетом условий:

• В банк «Пушкино» поступило
S0 20 000руб.
Р=20 %
• В банк «Шайковка» поступило S 0 45 000руб.
• В банк «Натарово» поступило
Р=15 %
S 0 90 000руб.
Р=12 %
•В банк «Дуброво» поступило S 10 000 руб.
0
Р=22 %
•В банк «Якимово» поступило S 12 000 руб.
0
Р=18 %

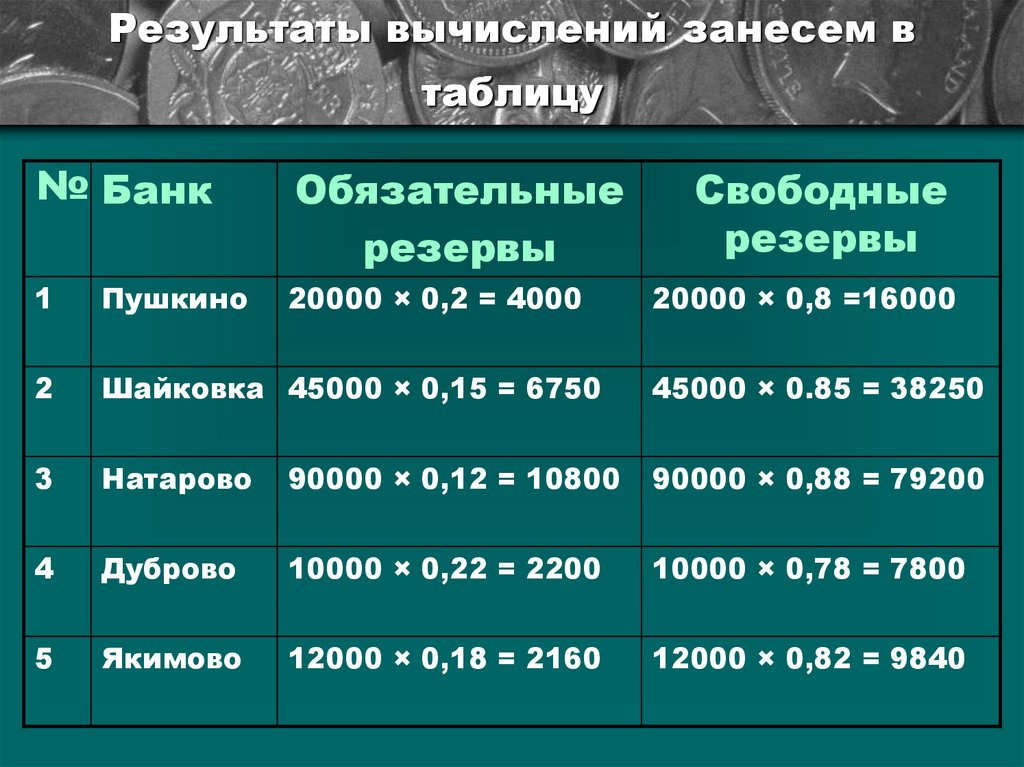
10. Результаты вычислений занесем в таблицу

№ Банк
Обязательные
резервы
1
Пушкино
20000 × 0,2 = 4000
2
Шайковка 45000 × 0,15 = 6750
45000 × 0.85 = 38250
3
Натарово
90000 × 0,12 = 10800
90000 × 0,88 = 79200
4
Дуброво
10000 × 0,22 = 2200
10000 × 0,78 = 7800
5
Якимово
12000 × 0,18 = 2160
12000 × 0,82 = 9840
Свободные
резервы
20000 × 0,8 =16000

11. Давайте обсудим вопрос:

• От чего и как зависят величины
свободных и обязательных
резервов, и может ли ЦБ влиять
на размер кредитов,
предоставляемых банками?

12. Задание классу:

• Записать величины обязательных и
свободных резервов в общем виде,
где S сумма вклада Р % обязательный резерв
0
Тогда величина обязательных резервов равна:
S0 P
S1
100
А свободных резервов
S 0 (100 P )
S2
S 0 S1
100

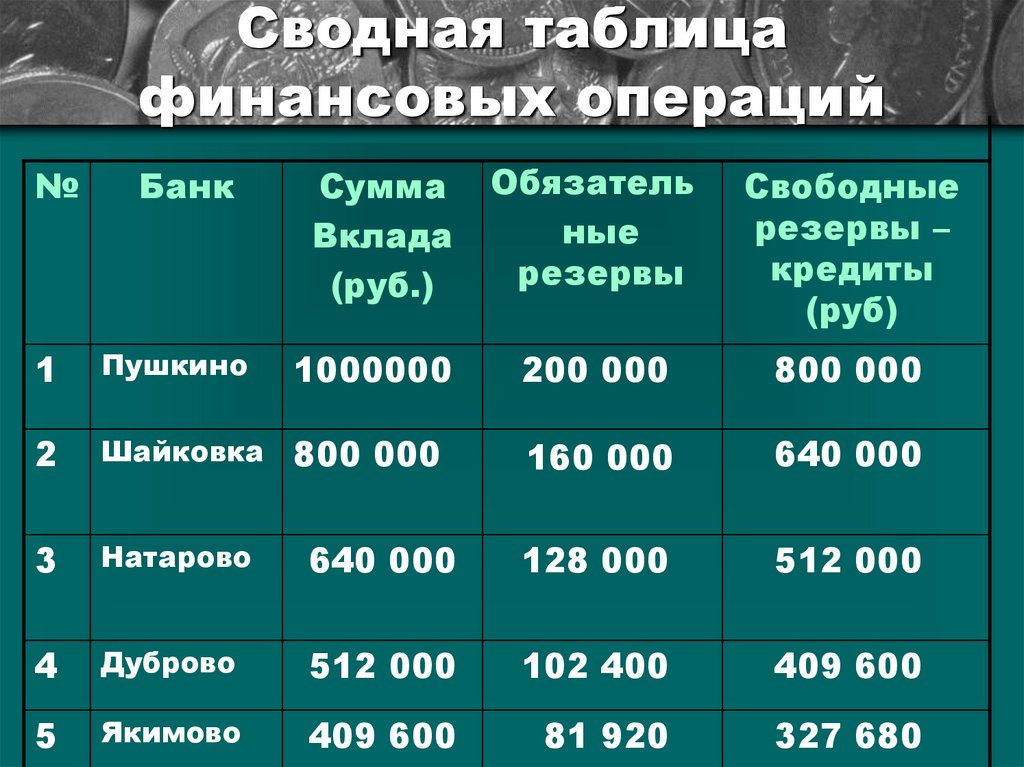
13. Сводная таблица финансовых операций

№
Банк
Сумма
Вклада
(руб.)
Обязатель
ные
резервы
Свободные
резервы –
кредиты
(руб)
1
Пушкино
1000000
200 000
800 000
2
Шайковка
800 000
160 000
640 000
3
Натарово
640 000
128 000
512 000
4
Дуброво
512 000
102 400
409 600
5
Якимово
409 600
81 920
327 680

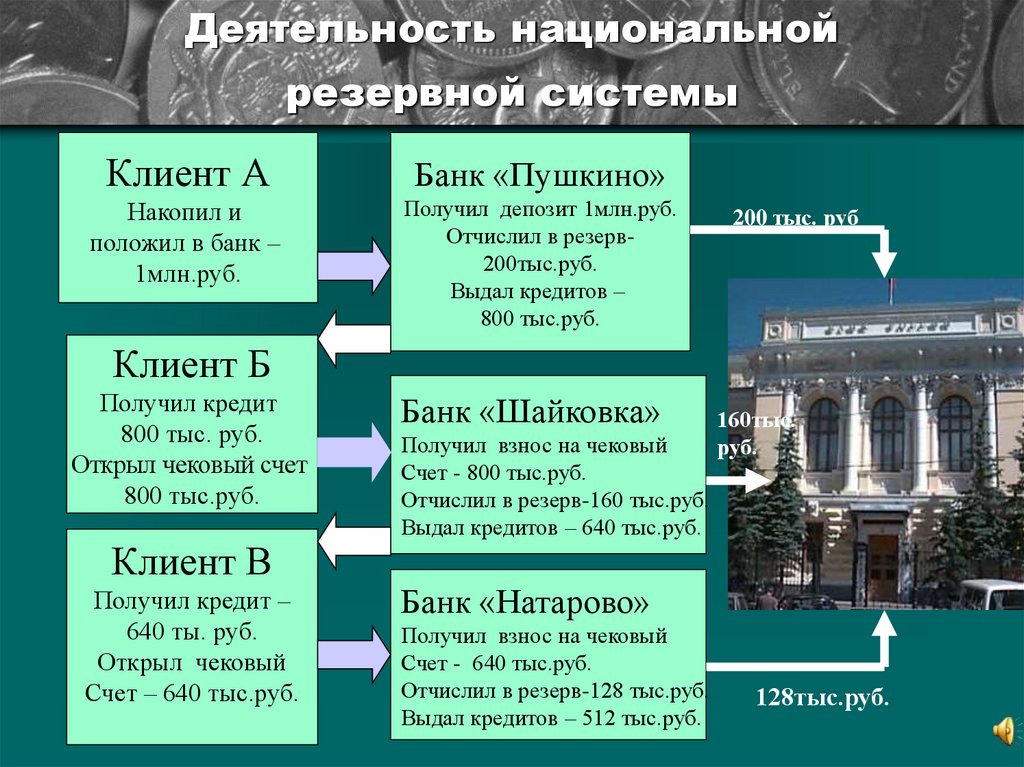
14. Деятельность национальной резервной системы

Клиент А
Банк «Пушкино»
Накопил и
положил в банк –
1млн.руб.
Получил депозит 1млн.руб.
Отчислил в резерв200тыс.руб.
Выдал кредитов –
800 тыс.руб.
200 тыс. руб
Клиент Б
Получил кредит
800 тыс. руб.
Открыл чековый счет
800 тыс.руб.
Клиент В
Получил кредит –
640 ты. руб.
Открыл чековый
Счет – 640 тыс.руб.
Банк «Шайковка»
Получил взнос на чековый
Счет - 800 тыс.руб.
Отчислил в резерв-160 тыс.руб.
Выдал кредитов – 640 тыс.руб.
160тыс.
руб.
Банк «Натарово»
Получил взнос на чековый
Счет - 640 тыс.руб.
Отчислил в резерв-128 тыс.руб.
Выдал кредитов – 512 тыс.руб.
128тыс.руб.

15. Задача классу:

• Как можно упростить и тем
самым ускорить операцию
подсчета суммы выданных
кредитов?

16. Вывод :

Свободные резервы системы банков
образуют последовательность:
800000;800000 (0,8);800000 (0,8) 2 ;800000 (0,8) 3 ;800000 (0,8) 4
т.е. первые пять членов геометрической прогрессии с
первым членом 800 000 и знаменателем 0,8.
По формуле суммы конечного числа геометрической
прогрессии получаем:
a1 (1 q 5 ) 800000(1 0,85 )
S5
2689280
1 q
1 0,8
Это сумма в 3.36 раза больше той суммы, которую
мог предоставить один банк «Пушкино» !

17. Задача классу:

• Обобщить полученный результат
на случай произвольных
значений a и q.
Ответ:
a1 (1 q )
a1 a1q
Sn
1 q
1 q 1 q
n
n
Решите задачу: Система состоит из трех
банков А, Б и В. В первый банк А внесен вклад
200 000 руб. Процентная ставка обязательных
резервов составляет 15%. Какова
максимальная сумма кредитов, которую может
выдать эта система?
ответ: 437325 (руб.)

18. Вывод:

a
a1
Sn 1
1 q
Вывод:
при очень больших n и 0<q<1величина
a1
Sn
1 q
это формула для нахождения суммы членов
бесконечной геометрической прогрессии.
Её экономический смысл состоит в том, что
при фиксированных значениях a1 и q она
указывает границу, предельные возможности
системы. Сколько банков мы бы не включали
в нее, выдать кредитов на сумму, равную или
большую числа
невозможно.
a
S
1
1 q

19. Итог урока:

Мы увидели, каким
образом приобретенные
знания по математике
могут быть сразу
использованы для решения
очень важных задач
современной экономики.
1.

20.

Сумма членов геометрической
прогрессии, бесконечно
убывающая прогрессия и её
сумма, имеют глубокий
экономический смысл. Решая
задачу о нахождении суммы n
членов геометрической
прогрессии, фактически нашли
возможность суммарного
кредитования, предоставляемых
системой, состоящей из n банков.
2.
учитель математики Габрусь Н.Ю.

21.

• Вы сегодня наглядно увидели о
необходимости функционирования
сложной системы коммерческих
банков. Ведь только с её помощью
некоторая сумма денег может
«вырасти» в несколько раз, участвуя во
многих сделках. А чем больше
кредитов будут выдавать банки, тем
больше различных проектов будет
осуществлено, тем, в конечном итоге,
богаче будет наша страна.
учитель экономики Клочкова Т.Н.

22. В качестве индивидуального задания на дом каждому ученику предлагается:

• сочинить систему, состоящую из шести
банков;
• назначить сумму, поступившую в первый банк
- системы;
• назначить процентную ставку обязательных
резервов;
• составить таблицу, аналогичную табл. 3;
• вычислить Sn — суммарную величину
кредитов, которые может предложить Ваша
система банков;
• определить предельные возможности
кредитования для построенной Вами системы
банков.