Теория движения военных колесных машин

1.

Слайды к лекциям по курсу
ТЕОРИЯ ДВИЖЕНИЯ
ВОЕННЫХ КОЛЕСНЫХ МАШИН
Лекция 8

2.

Распределение нормальных реакций
Нормальная реакция Rz на колесе КМ определяет радиус
качения rк, силу сопротивления качению и предельную
продольную реакцию по сцеплению Rxφ.
В общем случае при вычислении Rzi КМ рассматривают как
динамическую колебательную систему. Однако для решения
многих задач можно принять жесткую связь вала двигателя с
ведущими колесами, а также рассматривать стационарное
(установившееся) движение.
К установившемуся условно отнесем также движение с
постоянным ускорением при сохранении постоянной траектории
КМ.

3.

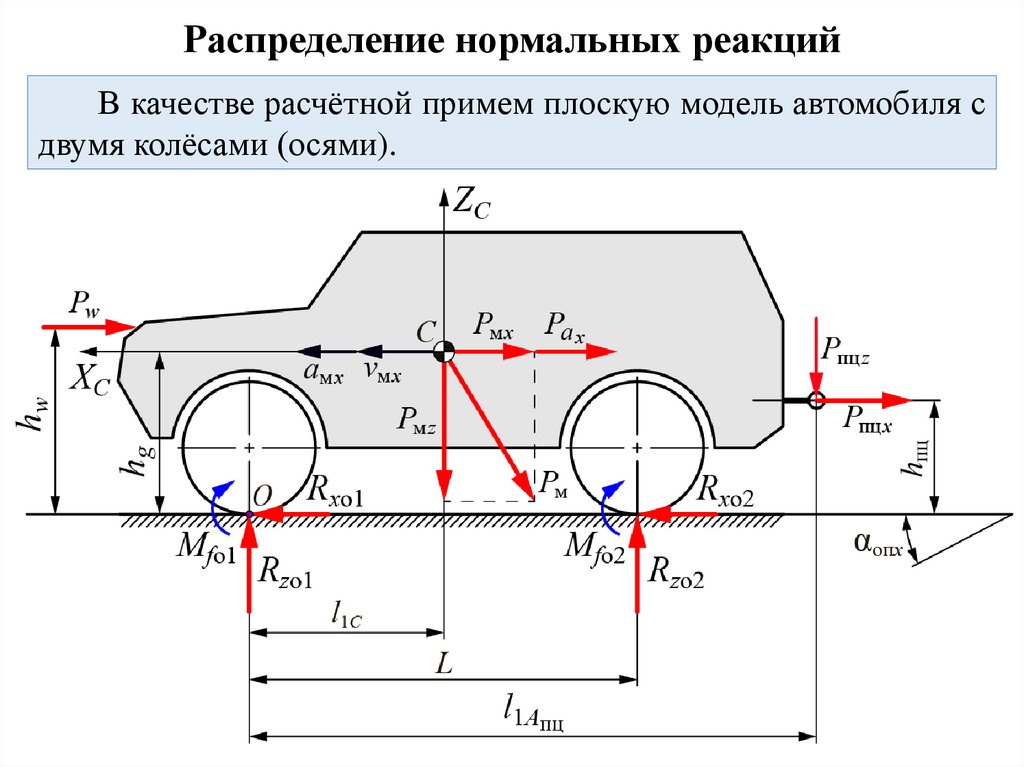
Распределение нормальных реакций
В качестве расчётной примем плоскую модель автомобиля с
двумя колёсами (осями).

4.

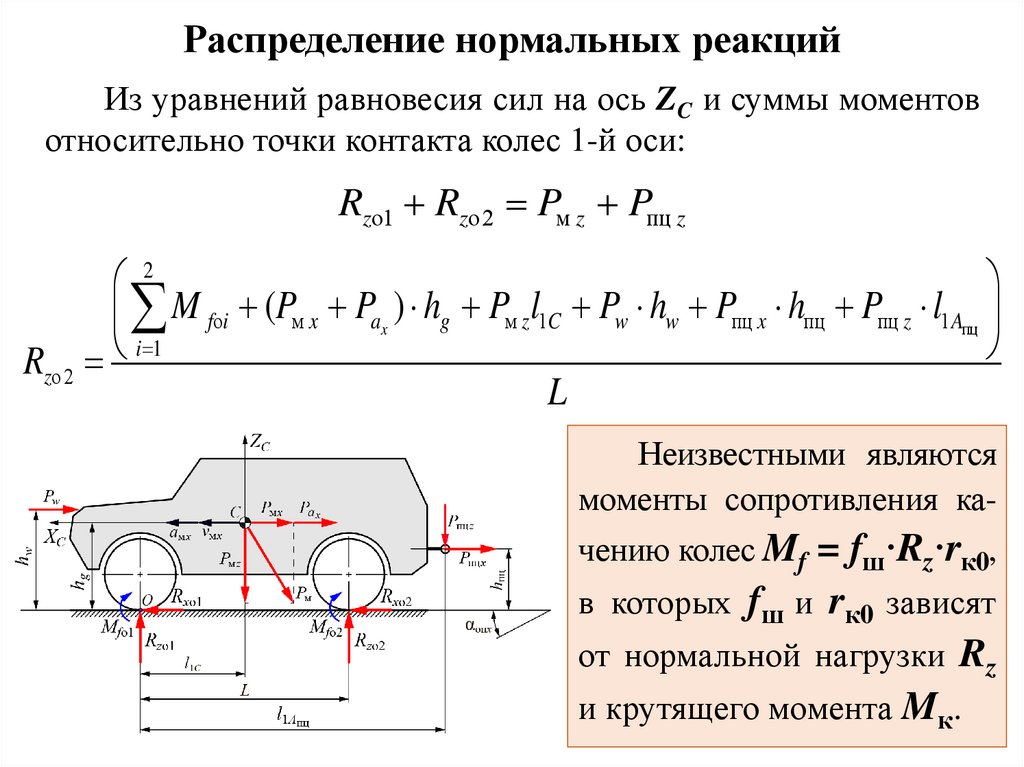
Распределение нормальных реакций
Из уравнений равновесия сил на ось ZC и суммы моментов
относительно точки контакта колес 1-й оси:
Rzо1 Rzо2 Pм z Pпц z
2
M fоi (Pм x Pax ) hg Pм zl1C Pw hw Pпц x hпц Pпц z l1 Aпц
Rzо2 i 1
L
Неизвестными являются
моменты сопротивления качению колес Mf = fш·Rz·rк0,
в которых fш и rк0 зависят
от нормальной нагрузки Rz
и крутящего момента Mк.

5.

Распределение нормальных реакций
С достаточной для практики точностью можно сделать три допущения:
• радиус rкв и коэффициент сопротивления качения в ведомом режиме
fшв, коэффициенты тангенциальной эластичности λM и λP определяются
нормальной реакцией при статическом положении КМ;
• в ведущем режиме
rк0 rкв M M к
f шM
f ш в rкв
M M к2
rк0
Rz rкв rк0
• крутящий момент Mк определяется из условия равномерного
распределения суммарного крутящего момента Mкм, необходимого
для преодоления сопротивления КМ, по всем nкM ведущим колесам:
M к M км nкM
где
M км Pw f шв Pм z Pм x Pпцx Pfп Pин rк0

6.

Распределение нормальных реакций
КМ с балансирной тележкой и реактивными штангами.
На КМ с числом осей больше двух часто используются
конструктивные схемы системы подрессоривания, объединяющие
две соседние оси. Классическим примером являются трехосные
машины с 2-й и 3-й осями, связанными балансирной системой
подрессоривания.

7.

Распределение нормальных реакций
Однако установка только одного балансира приводит к
перераспределению нормальных реакций по осям в тяговых
режимах. В ведущем режиме происходит уменьшение
нормальной реакции на 2-й оси и увеличение на 3-й.
Это неблагоприятно сказывается при движении по твердым
опорным поверхностям, приводя к повышенному износу шин и
возникновению циркуляции мощности. На деформируемых
опорных поверхностях возрастают деформации грунта и
сопротивление качению.
Для устранения этого недостатка в конструкцию вводятся
реактивные штанги, воспринимающие реактивные моменты
ведущих осей и обеспечивающие выравнивание нормальных
реакций по осям.

8.

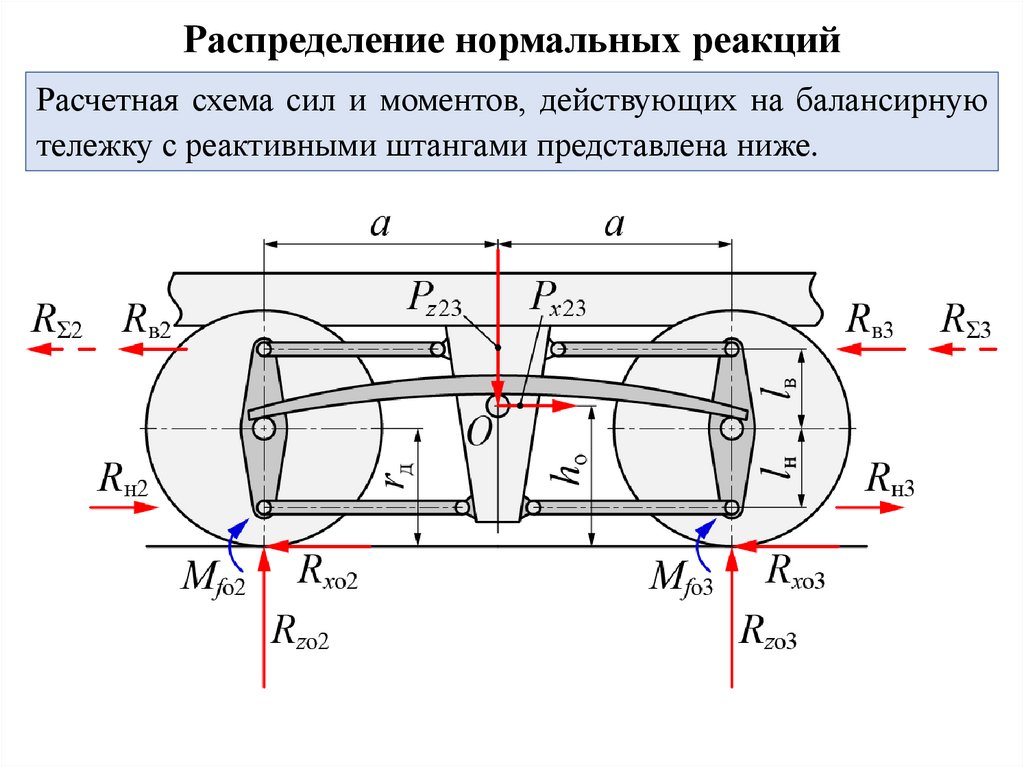
Распределение нормальных реакций
Расчетная схема сил и моментов, действующих на балансирную
тележку с реактивными штангами представлена ниже.

9.

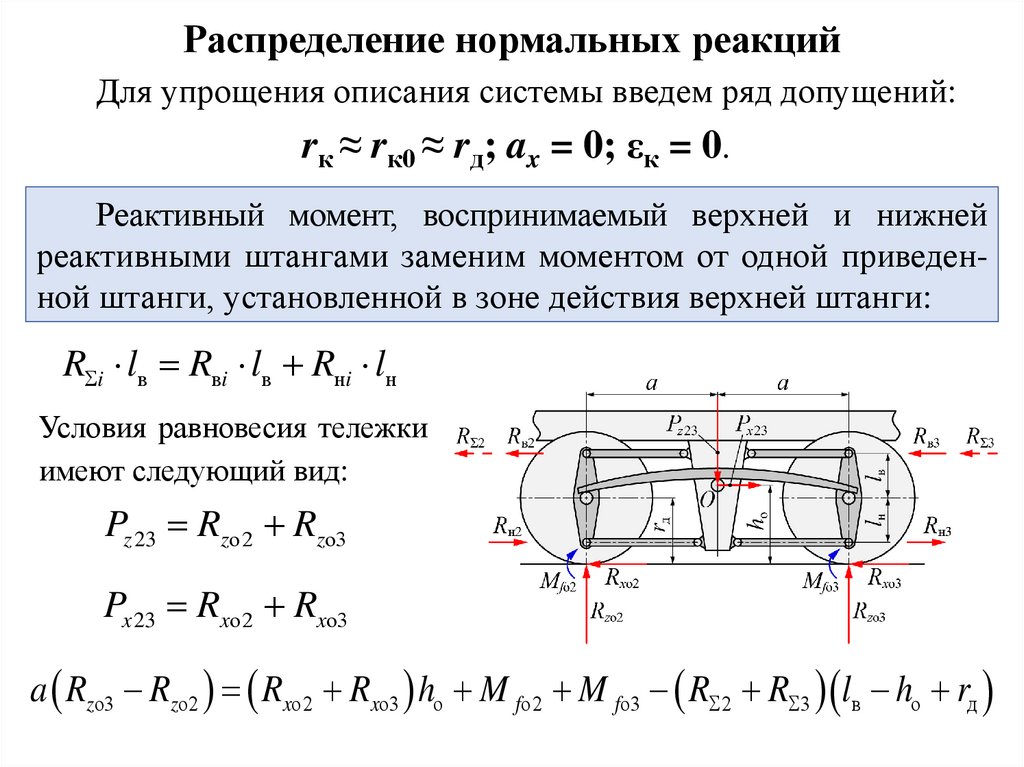
Распределение нормальных реакций
Для упрощения описания системы введем ряд допущений:
rк ≈ rк0 ≈ rд; ax = 0; εк = 0.
Реактивный момент, воспринимаемый верхней и нижней
реактивными штангами заменим моментом от одной приведенной штанги, установленной в зоне действия верхней штанги:
R i lв Rвi lв Rнi lн
Условия равновесия тележки
имеют следующий вид:
Pz 23 Rzо2 Rzо3
Px 23 Rxо2 Rxо3
a Rzо3 Rzо2 Rxо2 Rxо3 hо M fо2 M fо3 R 2 R 3 lв hо rд

10.

Распределение нормальных реакций
Уравнения равновесия моментов на одном колесе:
R lв M к Rx rд M fш
Подставив выражения RΣi в уравнение суммы моментов для
тележки, после преобразований получим:
rд M fо2 M fо3 hо rд
a Rzо3 Rzо2 Rxо2 Rxо3 hо rд 1
lв
lв
При hо = rд правая часть этого уравнения равна нулю, и,
следовательно, равны нормальные реакции Rzо2 = Rzо3.

11.

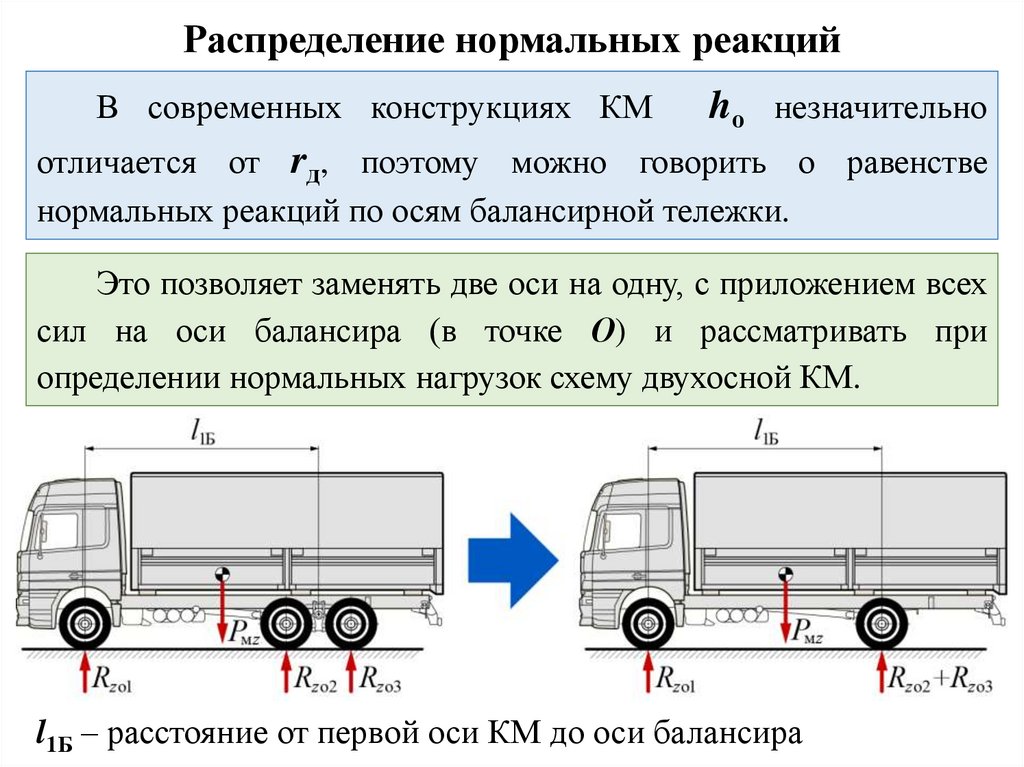
Распределение нормальных реакций
В современных конструкциях КМ
hо незначительно
отличается от rд, поэтому можно говорить о равенстве
нормальных реакций по осям балансирной тележки.
Это позволяет заменять две оси на одну, с приложением всех
сил на оси балансира (в точке О) и рассматривать при
определении нормальных нагрузок схему двухосной КМ.
l1Б – расстояние от первой оси КМ до оси балансира

12.

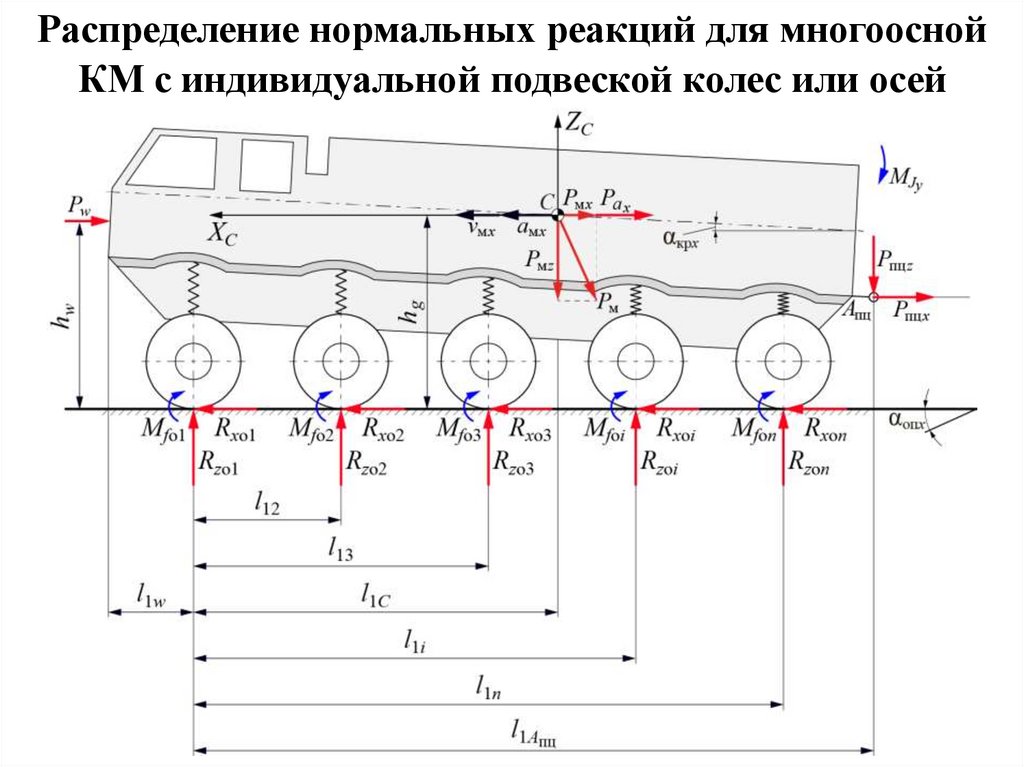
Распределение нормальных реакций для многоосной
КМ с индивидуальной подвеской колес или осей

13.

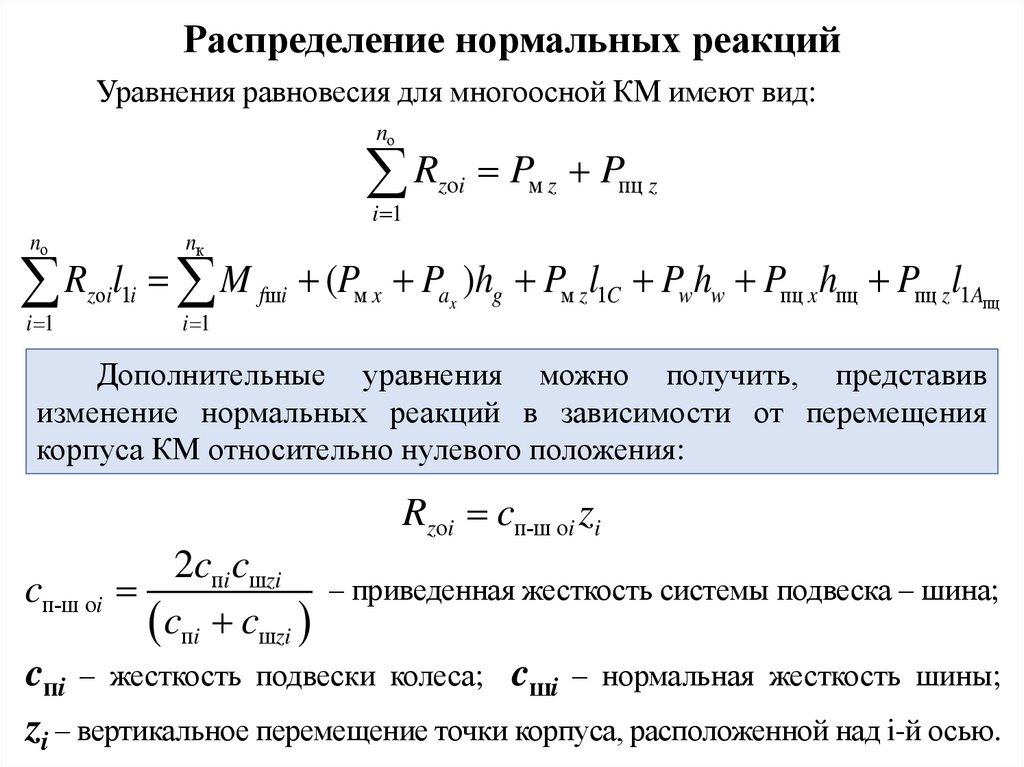
Распределение нормальных реакций
Уравнения равновесия для многоосной КМ имеют вид:
nо
R
i 1
nо
R
i 1
zоi
Pм z Pпц z
nк
l M fшi (Pм x Pax )hg Pм zl1C Pwhw Pпц x hпц Pпц zl1 Aпц
zоi 1i
i 1
Дополнительные уравнения можно получить, представив
изменение нормальных реакций в зависимости от перемещения
корпуса КМ относительно нулевого положения:
Rzоi cп-ш оi zi
cп-ш оi
2cпi cшzi
cпi cшzi
– приведенная жесткость системы подвеска – шина;
cпi – жесткость подвески колеса; cшi – нормальная жесткость шины;
zi – вертикальное перемещение точки корпуса, расположенной над i-й осью.

14.

Распределение нормальных реакций
Перемещение zi для i-й оси можно выразить (для абсолютно
жесткой рамы) через перемещение корпуса над 1-й осью z1 и угол
наклона (дифферента) корпуса αкр x под действием внешних сил:
zi z1 l1i tg кр x
Обозначив для удобства
nк
A0 M fшi (Pм x Pax )hg Pм zl1C Pwhw Pпц x hпц Pпц zl1 Aпц
i 1
nо
nо
A1 cп-шоi
A2 cп-шоil1i
i 1
A0 А3 tg кр x
A2
A3 cп-шоil12i
i 1
после решения уравнений получаем
z1
nо
tg кр x
i 1
Pмz Pпцz A2 A0 А1
A22 A1 A3
Rzоi cп-шоi z1 l1i tg кр x

15.

Расчет нормальных реакций для трехосной КМ
Для многоосных КМ можно принять, что кузов КМ является
жестким, а жесткость упругих элементов на всех осях примерно
одинакова.
Тогда для плоской (велосипедной) схемы движения КМ можно
сделать допущение, что концы векторов нормальных реакций лежат
на одной прямой.

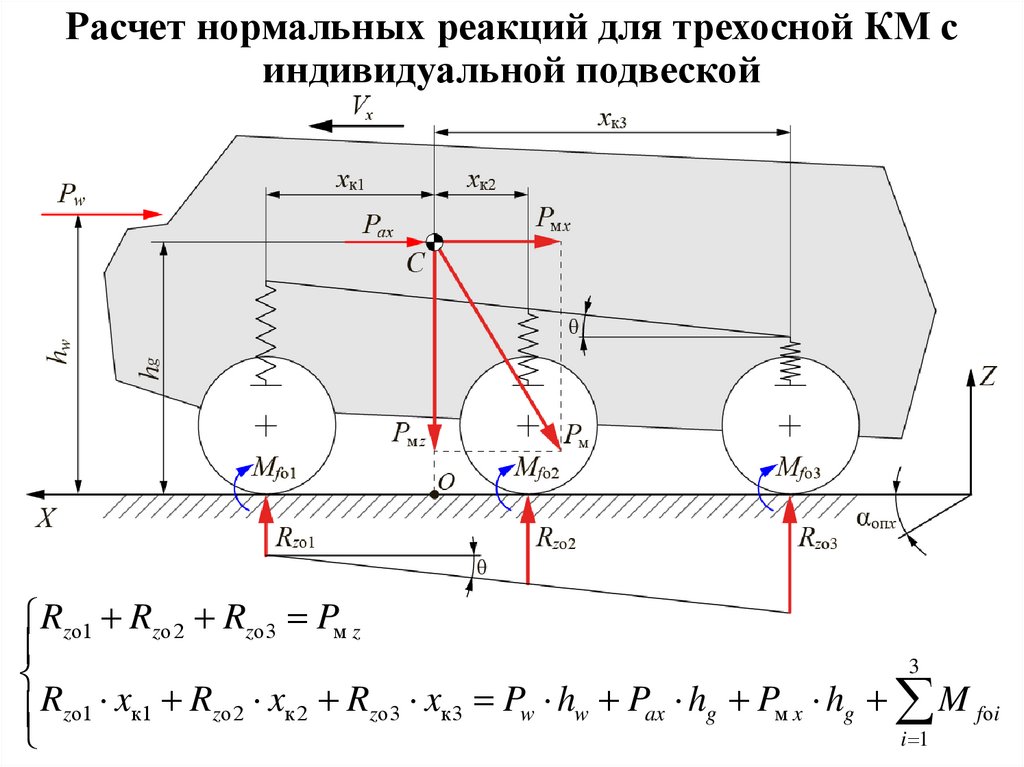
16.

Расчет нормальных реакций для трехосной КМ с
индивидуальной подвеской
Rzо1 Rzо2 Rzо3 Pм z
3
Rzо1 xк1 Rzо2 xк 2 Rzо3 xк3 Pw hw Pax hg Pм x hg M fоi
i 1

17.

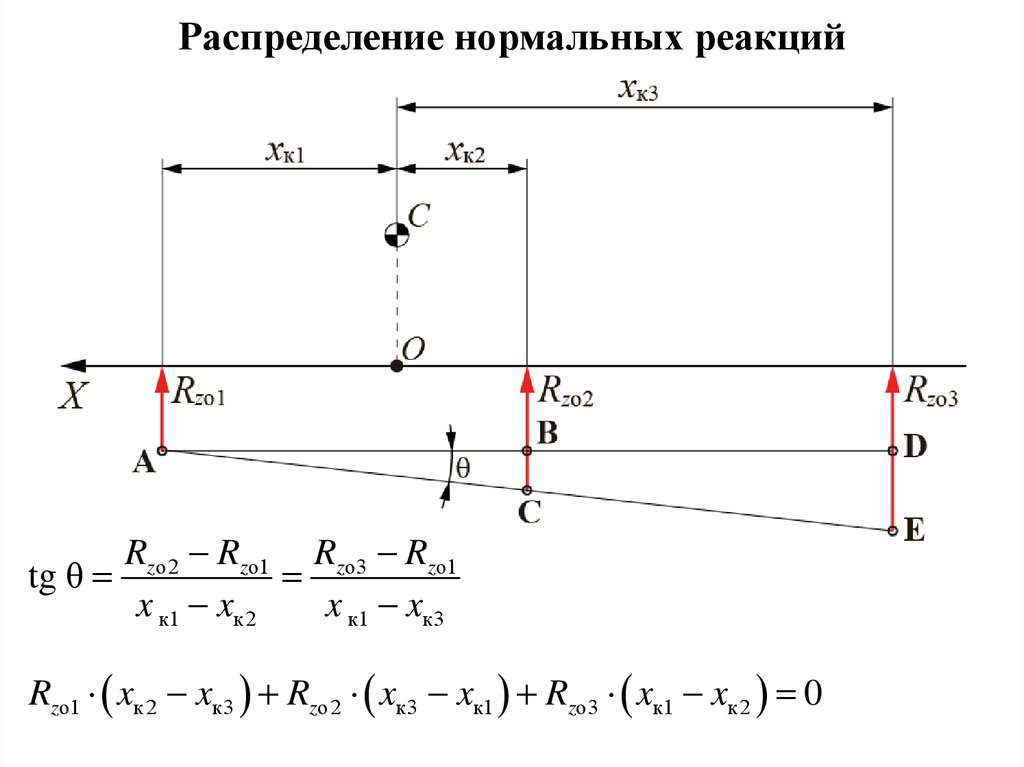
Распределение нормальных реакций
Rzо2 Rzо1 Rzо3 Rzо1
tg θ
x к1 xк 2
x к1 xк3
Rzо1 xк 2 xк3 Rzо2 xк3 xк1 Rzо3 xк1 xк 2 0

18.

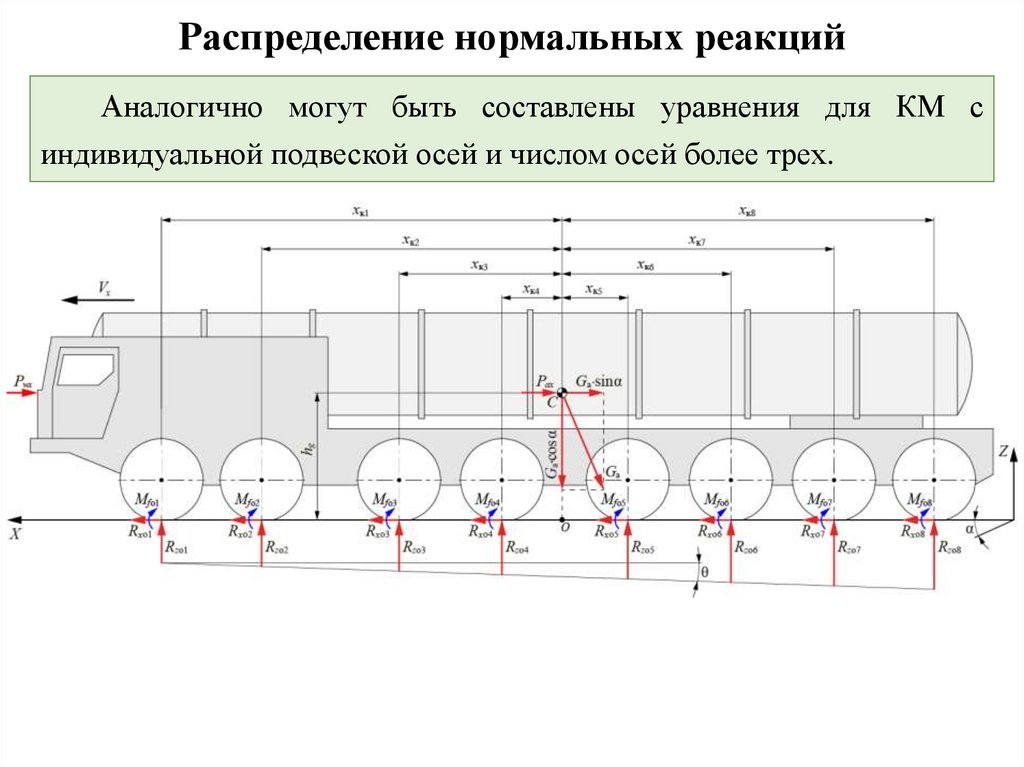
Распределение нормальных реакций
Аналогично могут быть составлены уравнения для КМ с
индивидуальной подвеской осей и числом осей более трех.