Similar presentations:
Формальные теории и исчисления. Модуль 3
1.
Модуль 3Формальные теории и
исчисления
Занятие 3.4. Исчисление
предикатов
2020 г.
2.
Содержание1.
Алфавит исчисления предикатов
2.
Формулы исчисления предикатов
3.
Аксиомы исчисления предикатов
4.
5.
Правила вывода исчисления
предикатов
Свойства исчисления предикатов
3.
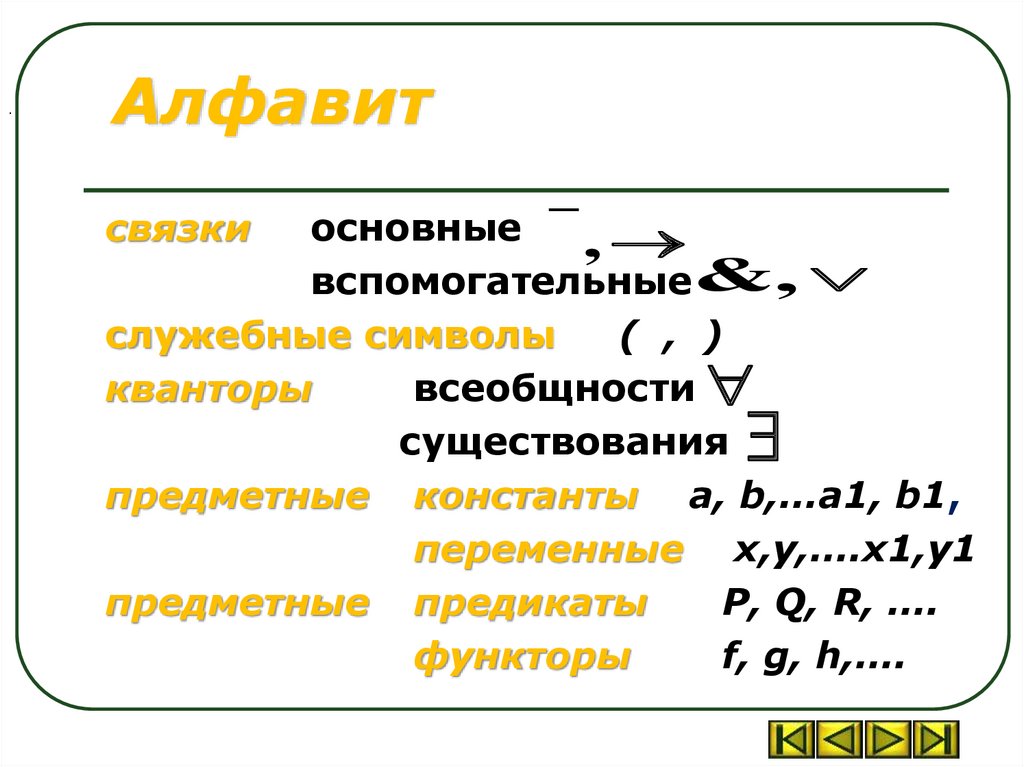
.Алфавит
связки
основные
,
вспомогательные&,
служебные символы
( , )
кванторы
всеобщности
существования
предметные константы a, b,…a1, b1,
переменные x,y,….x1,y1
предметные предикаты
P, Q, R, ….
функторы
f, g, h,….
4.
Формулы<формула> ::= <атом>│
│<формула> <формула>│
│<переменная><формула>│
│переменная><формула>
<атом>::= <предикат>( <список
термов> )
<список термов> ::= <терм>
│<терм> , <список термов>
<терм>::= <константа> │<переменная>│
│<функтор>(<список термов>)
5.
АксиомыP1 : xA( x ) A( t )
P2 : A( t ) xA( x )
И все аксиомы исчисления
высказываний
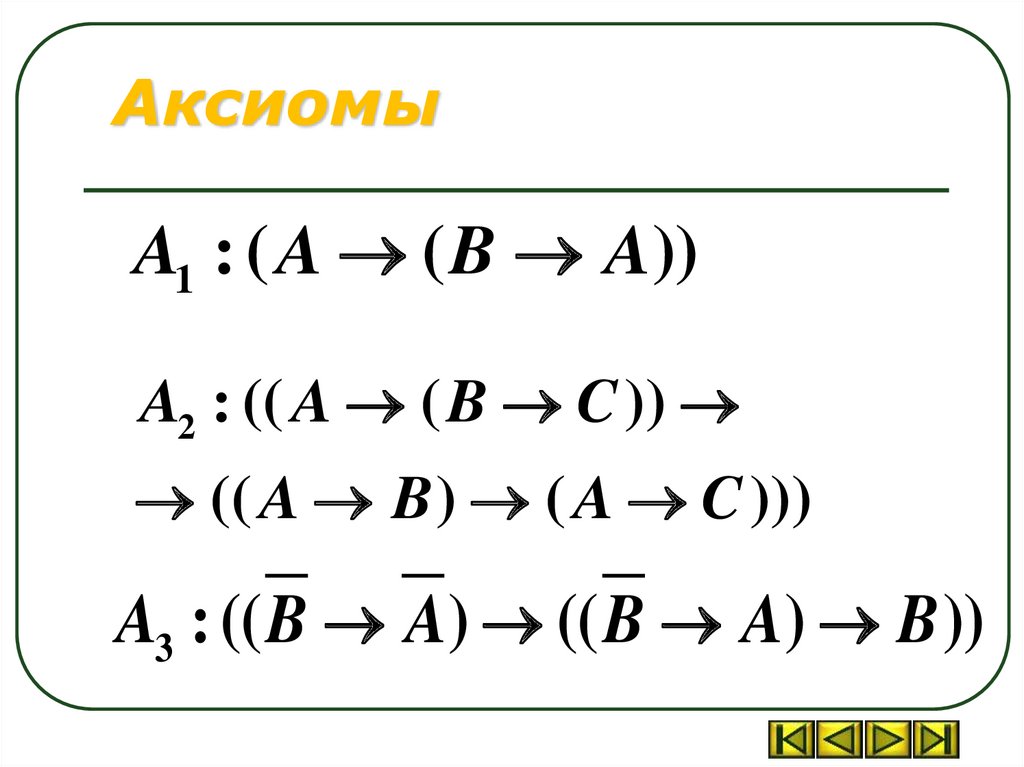
6.
АксиомыA1 : ( A ( B A))
A2 : (( A ( B C ))
(( A B ) ( A C )))
A3 : (( B A) (( B A) B ))
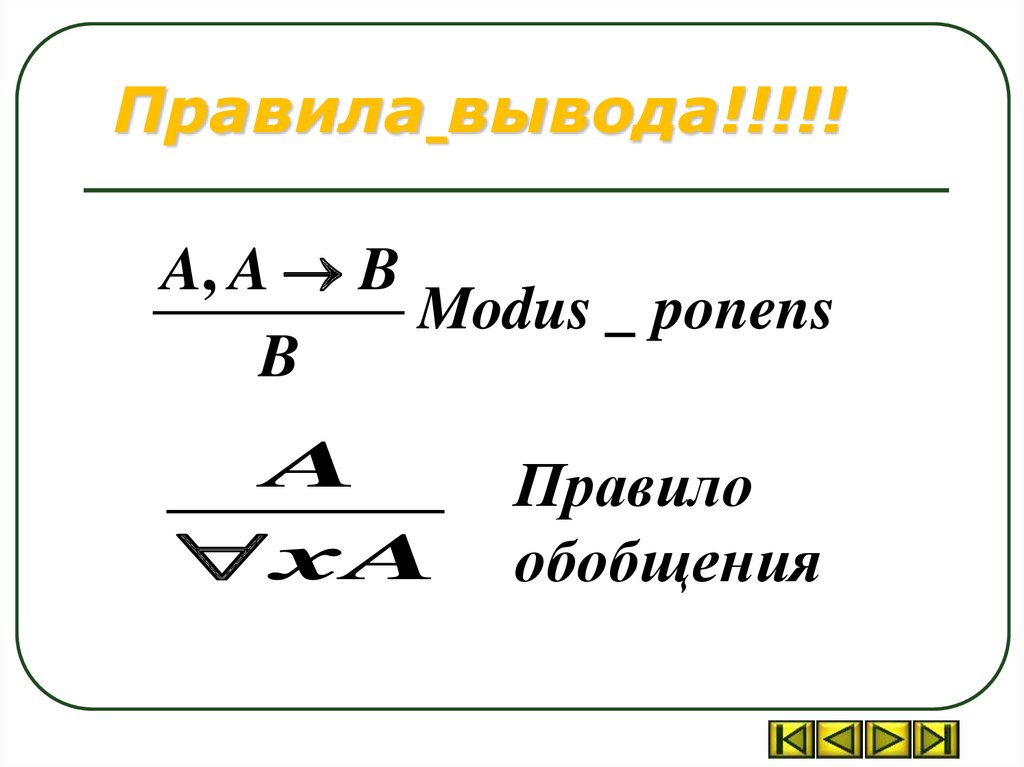
7.
Правила вывода!!!!!A, A B
Modus _ ponens
B
A
xA
Правило
обобщения
8.
Равносильные формулы1.Равносильности для двойственности
2.Равносильности
для
квантора всеобщности
конъюнкции
и
3.Равносильности
для
квантора существования
дизъюнкции
и
4. Вынесение константы
9.
Равносильности длядвойственности
xP ( x ) xP ( x )
xP ( x ) xP ( x )
xP ( x ) x P ( x )
xP ( x ) x P ( x )
10.
Равносильности для &x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
x yP ( x , y ) y xP ( x , y )
11.
Равносильности для Vx( P ( x ) Q( x )) xP ( x ) xQ( x )
x yP ( x , y ) y xP ( x , y )
12.
Вынесение константыx(С & Q( x )) С & xQ( x )
x(С Q( x )) С xQ( x )
x(С & Q( x )) С & xQ( x )
x(С Q( x )) С xQ( x )
x(С Q( x )) С xQ( x )
x(С Q( x )) С xQ( x )
13.
Пример №1Показать равносильность
формулы
x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
14.
Решение примера №11. Если предикаты P(x) и Q(x) тождественно
истинны,
то тождественно истинен
предикат
P ( x ) & Q( x ) , а поэтому, будут
истинны высказывания
xP ( x )
xQ( x )
x( P ( x ) & Q( x ))
2. Если один из предикатов, например, P(x),
будет не тождественно истинен, то предикат
P( x ) & Q( x ) не будет тождественно истинен,
следовательно, ложными будут высказывания
xP ( x )
x( P ( x ) & Q( x ))
15.
Решение примера №13. Если оба предиката P(x) и Q(x) не будут
тождественно истинны, то не будет
тождественно истинен предикат P ( x ) & Q( x )
Следовательно, будут ложными высказывания
xP ( x )
xQ( x )
x( P ( x ) & Q( x ))
4. Следовательно, обе части равносильности
равны при любых значениях P(x) и Q(x)
x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
16.
Общезначимость ивыполнимость
Формула А выполнима в области М,
если существуют значения
переменных, входящих в эту формулу
и отнесенных к области М, при которых
формула принимает и истинные
значения
Формула А выполнима, если
существует область, на которой она
выполнима
17.
Общезначимость ивыполнимость
Формула А тождественно истинна в области
М, если она принимает истинные значения
для всех значений переменных, входящих в
эту формулу и отнесенных к этой области
Формула А тождественно ложна в области
М, если она принимает ложные значения для
всех значений переменных, входящих в эту
формулу и отнесенных к этой области
Формула А общезначима, если она
тождественно истинна во всякой области
18.
Общезначимость ивыполнимость
1.Если формула А общезначима, то
она и выполнима на любой
области
2.Если формула А
тождественно
истинна в области М, то она и
выполнима в этой области
3.Если формула А невыполнима, то
она тождественно ложна в любой
области
19.
Пример № 2Показать
общезначимость
правила обобщения квантора
всеобщности
B A( x )
правило
B xA( x )
20.
Решение примера № 21.
R ( B A( x )) ( B xA( x ))
2.
R ( B A( x )) ( B xA( x ))
3. R ( B A( x )) x ( B A( x ))
R Z ( x ) xZ ( x ) 1, где _ Z ( x ) B A( x )
Так как формула R тождественно истинна в
любой области, значит она общезначима
21.
РазрешимостьСуществует
ли
алгоритм,
позволяющий для любой формулы
установить,
является
ли
она
общезначимой, выполнимой или
тождественно ложной?
Теорема Черча
Проблема разрешимости
исчисления предикатов в
общем виде неразрешима


















 mathematics
mathematics








