Алгоритмы и элементы программирования. Алгоритмы исследования элементарных функций

1.

Раздел 3 Алгоритмы и элементы программирования
Глава 3.1 Алгоритмы и структуры данных
Тема 3.1.1 Алгоритмы исследования элементарных функций

2.

Алгоритм — конечная совокупность
точно
заданных
правил
решения
произвольного класса задач или набор
инструкций, описывающих порядок действий
исполнителя для решения некоторой задачи.

3.

Свойства алгоритмов
Дискретность — алгоритм должен
представлять процесс решения задачи как
последовательное выполнение некоторых
простых шагов. При этом для выполнения
каждого шага алгоритма требуется конечный
отрезок времени, то есть преобразование
исходных данных в результат осуществляется
во времени дискретно.

4.

Свойства алгоритмов
Понятность — алгоритм должен
включать только те команды,
которые доступны исполнителю и
входят в его систему команд.

5.

Свойства алгоритмов
Массовость (универсальность).
Алгоритм должен быть применим к
разным наборам начальных данных.
Результативность — завершение
алгоритма определёнными
результатами.

6.

Свойства алгоритмов
Детерминированность (определённость).
В каждый момент времени следующий шаг работы
однозначно определяется состоянием системы.
Таким образом, алгоритм выдаёт один и тот же
результат (ответ) для одних и тех же исходных
данных.

7.

Свойства алгоритмов
Завершаемость (конечность) — в более узком
понимании алгоритма как математической функции,
при правильно заданных начальных данных
алгоритм должен завершать работу и выдавать
результат за определённое число шагов.

8.

Способы задания алгоритмов
Словесный (запись на естественном языке)
Графический (изображения из графических символов)
Псевдокод
(полуформализованное описание алгоритмов на
условном алгоритмическом языке, включающее в себя как элементы
языка программирования, так и фразы естественного языка,
общепринятые математические обозначения и др.)
Программный (тексты на языках программирования)

9.

Пример словесного способа задания алгоритма
Алгоритм Евклида (нахождения (НОД) двух натуральных
чисел)
1) Задать два числа.
2) Если числа равны, то взять любое из них в качестве
ответа и остановиться, в противном случае продолжить
выполнение алгоритма.
3) Определить большее из чисел.
4) Заменить большее из чисел разностью большего и
меньшего из чисел.
5) Повторить алгоритм с шага 2.

10.

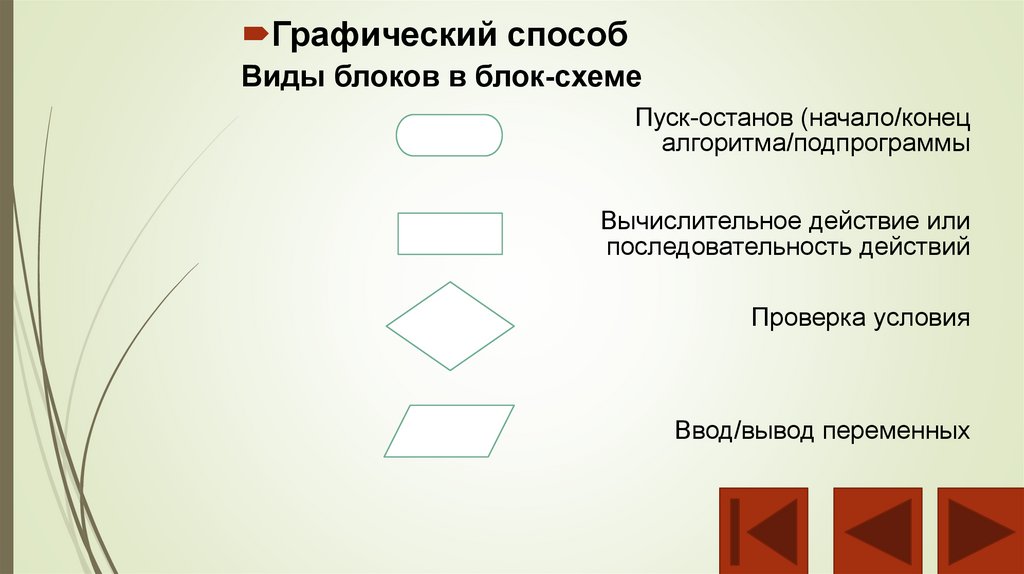
Графический способ
Виды блоков в блок-схеме
Пуск-останов (начало/конец
алгоритма/подпрограммы
Вычислительное действие или
последовательность действий
Проверка условия
Ввод/вывод переменных

11.

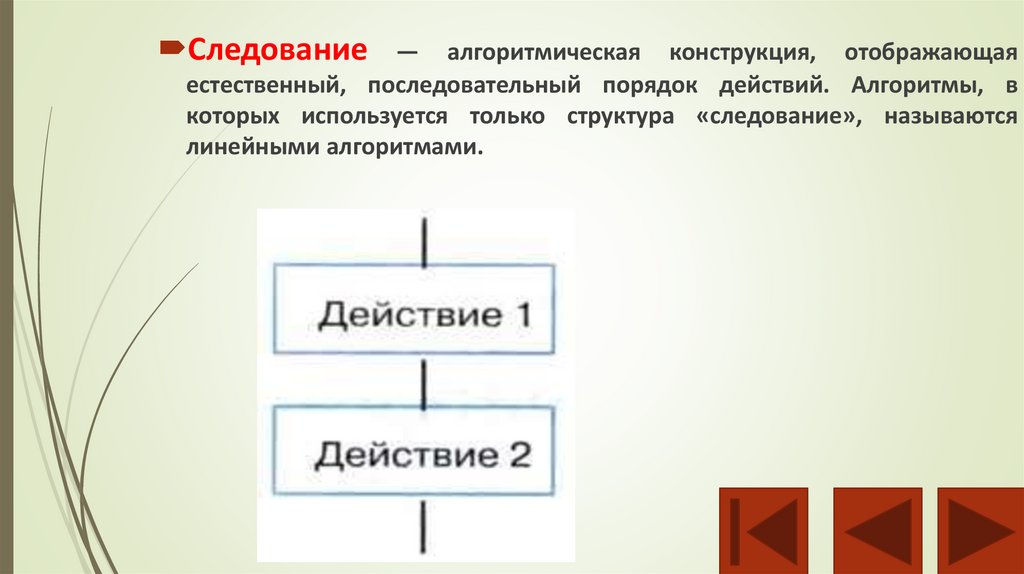
Следование
— алгоритмическая конструкция, отображающая
естественный, последовательный порядок действий. Алгоритмы, в
которых используется только структура «следование», называются
линейными алгоритмами.

12.

Пример
Дан фрагмент линейного алгоритма:
х=2
у=х*х
У=У*У
х=у*х
s=x+y
Выясним, какое значение получит
переменная s после выполнения этого фрагмента
алгоритма. Для этого составим таблицу значений
переменных, задействованных в алгоритме:

13.

Ветвление — алгоритмическая конструкция, в которой в зависимости от
результата проверки условия («да» или «нет») предусмотрен выбор
одной из двух последовательностей действий (ветвей). Алгоритмы, в
основе
которых
лежит
структура
«ветвление»,
называют
разветвляющимися.

14.

Пример
Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит
данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.

15.

Пример
Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, В
и С.
Пусть А = 10, В = 30 и С = 20.
Тогда процесс выполнения алгоритма можно представить в следующей
таблице:

16.

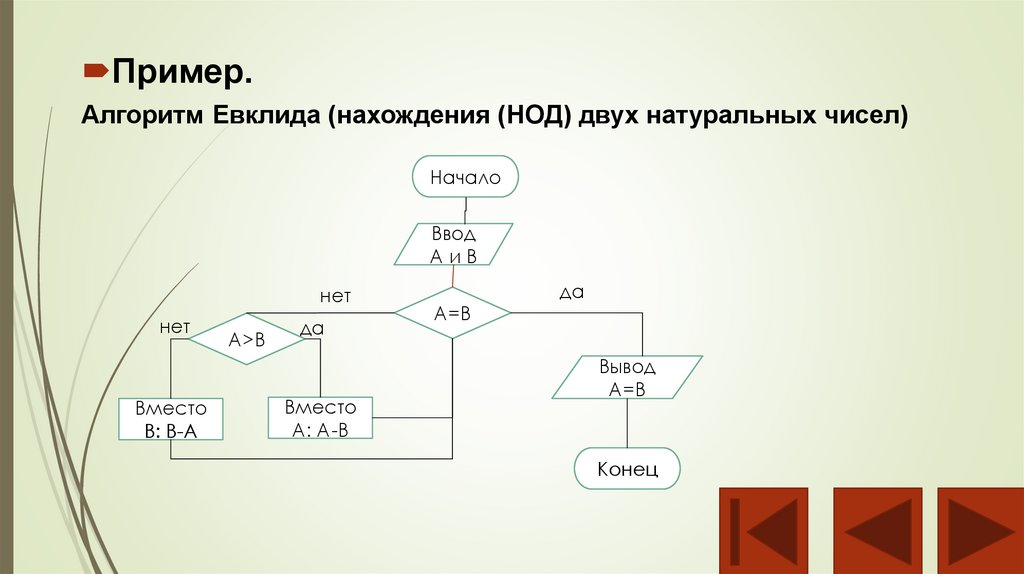
Пример.
Алгоритм Евклида (нахождения (НОД) двух натуральных чисел)
Начало
Ввод
АиВ
нет
нет
Вместо
В: В-А
А>В
да
Вместо
А: А-В
А=В
да
Вывод
А=В
Конец

17.

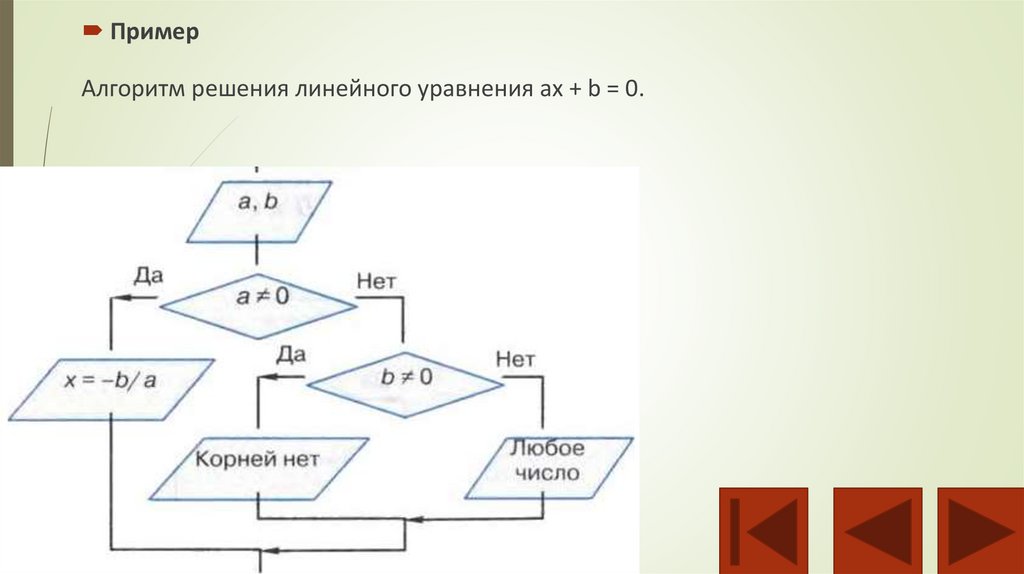
Пример
Алгоритм решения линейного уравнения ax + b = 0.

18.

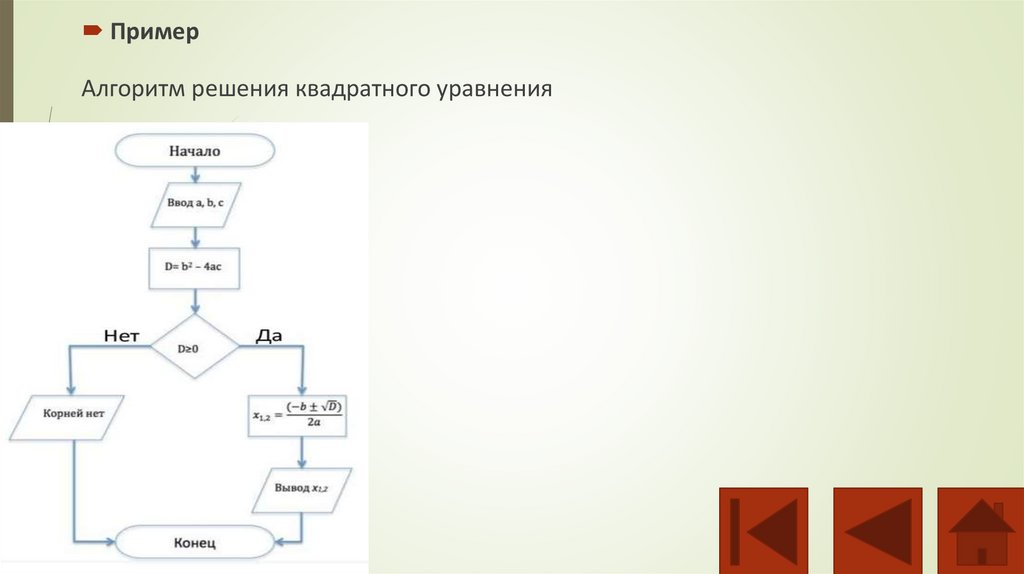
Пример
Алгоритм решения квадратного уравнения