Similar presentations:
Аналитическая геометрия. Часть 2. Геометрия в пространстве
1. Аналитическая геометрия
Часть 2Геометрия в пространстве
2. Аналитическая геометрия в пространстве.
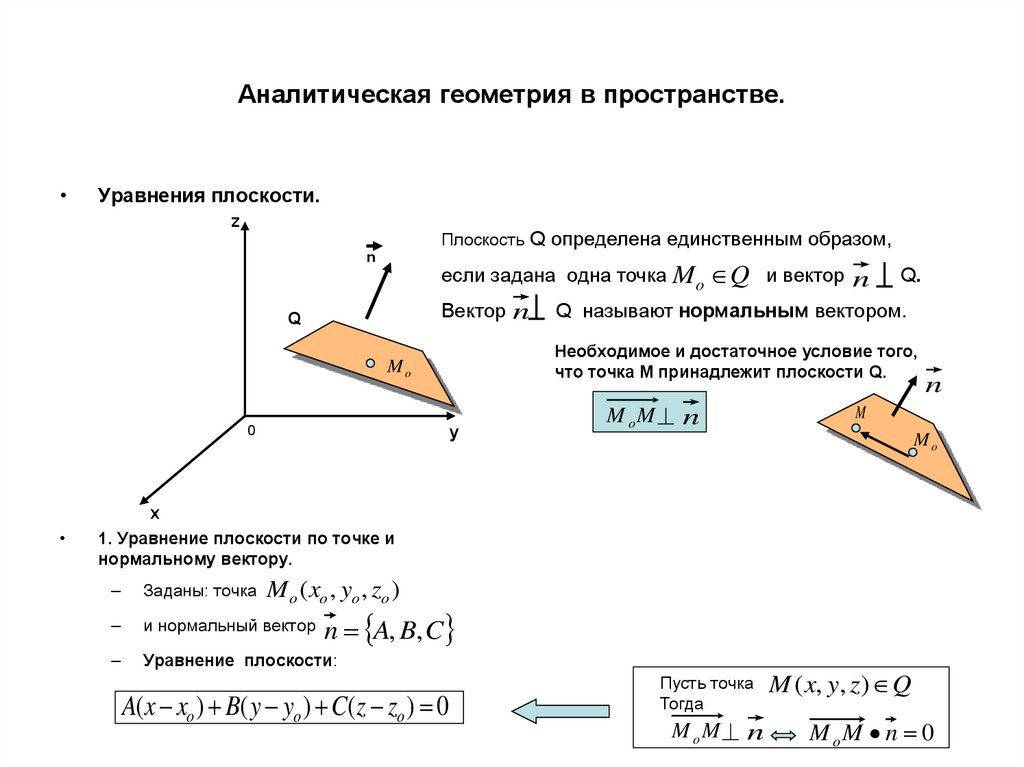
Уравнения плоскости.
z
Плоскость Q определена единственным образом,
n
если задана одна точка M o Q и вектор n
Вектор n
Q
Q называют нормальным вектором.
Необходимое и достаточное условие того,
что точка М принадлежит плоскости Q.
Mo
0
Q.
y
M oM
n
M
n
Mo
х
1. Уравнение плоскости по точке и
нормальному вектору.
M o ( xo , yo , zo )
–
Заданы: точка
–
и нормальный вектор
–
Уравнение плоскости:
n A, B, C
A( x xo ) B( y yo ) C( z zo ) 0
Пусть точка
Тогда
M oM
n
M ( x, y, z) Q
M oM n 0
3. Аналитическая геометрия в пространстве.
2. Общее уравнение плоскости.
–
Уравнение вида
–
–
называется общим уравнением плоскости.
Коэффициенты A,B,C в уравнении определяют
координаты нормального вектора:
Ax By Cz D 0
n A, B, C
Теорема.
Всякое уравнение первой степени
с тремя переменными x,y,z вида
Ax By Cz D 0
(1)
задает плоскость в пространстве
и наоборот, всякая плоскость
в пространстве может быть задана
уравнением с тремя переменными x,y,z
вида (1).
n A, B, C
Q
Q
4. Аналитическая геометрия в пространстве.
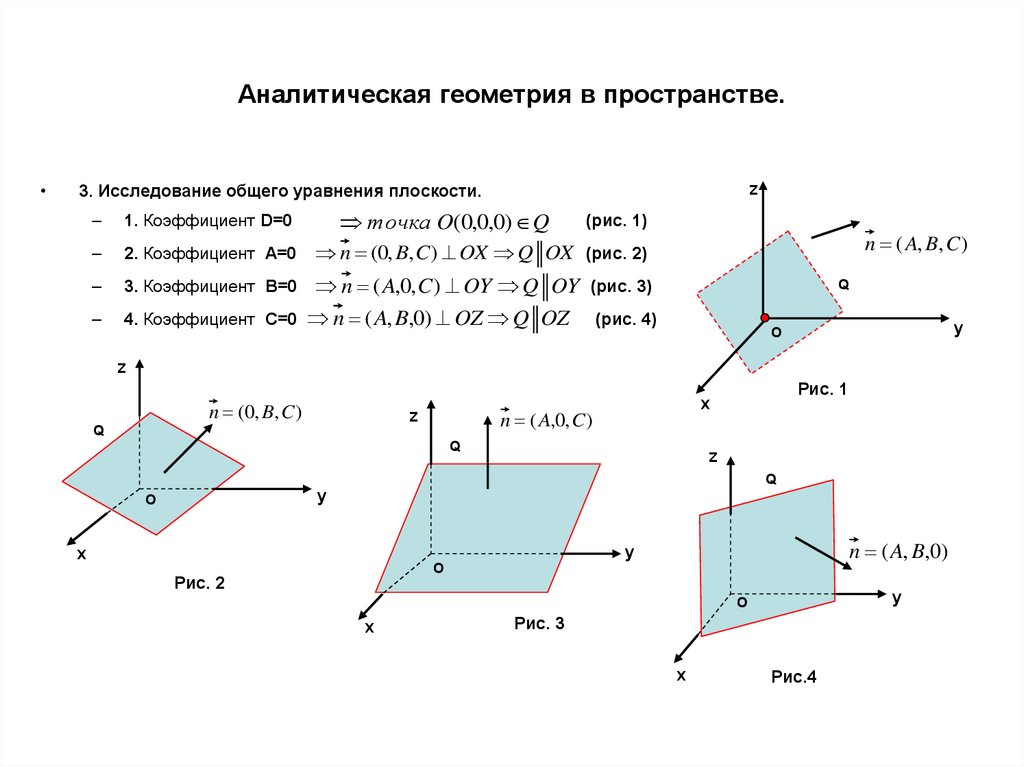
3. Исследование общего уравнения плоскости.
–
1. Коэффициент D=0
–
2. Коэффициент A=0
–
3. Коэффициент B=0
–
z
точка O(0,0,0) Q
(рис. 1)
n ( A, B, C )
n (0, B, C) OX Q OX (рис. 2)
n ( A,0, C) OY Q OY (рис. 3)
4. Коэффициент C=0 n ( A, B,0) OZ Q OZ
(рис. 4)
Q
y
O
z
n (0, B, C )
n ( A,0, C )
z
Q
Рис. 1
x
Q
z
Q
y
O
n ( A, B,0)
y
x
O
Рис. 2
y
O
x
Рис. 3
x
Рис.4
5. Аналитическая геометрия в пространстве.
–5. Коэффициенты A=B=0
–
6. Коэффициенты A=C=0
–
7. Коэффициенты B=C=0
n (0,0, C) OZ Q OZ (рис. 5)
n (0, B,0) OY Q OY (рис. 6)
n ( A,0,0) OX Q OX (рис. 7)
z
z
n (0,0, C )
Q
z
n (0, B,0)
Q
Q
O
y
O
n (A,0,0)
y
O
x
x
x
Рис. 5
Рис. 6
Рис. 7
y
6. Аналитическая геометрия в пространстве.
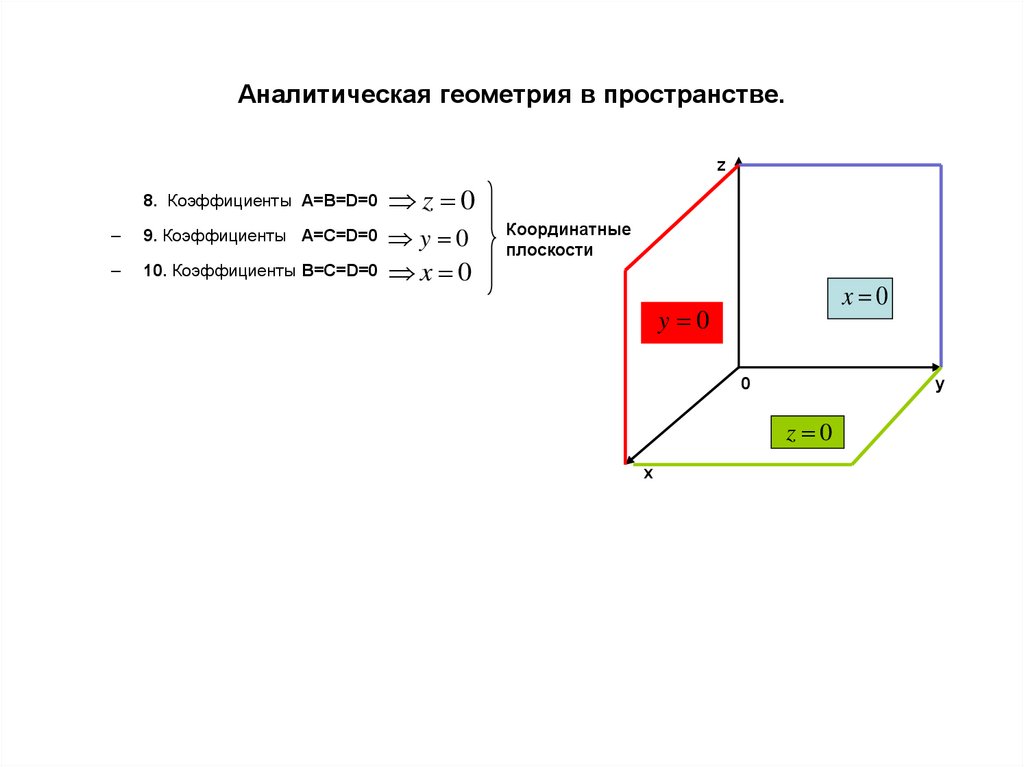
z8. Коэффициенты A=B=D=0
z 0
–
9. Коэффициенты A=C=D=0
y 0
–
10. Коэффициенты B=C=D=0
x 0
Координатные
плоскости
x 0
y 0
0
y
z 0
x
7. Аналитическая геометрия в пространстве.
Уравнения прямой в пространстве.
1. Общее уравнение прямой.
– Аксиома: линия пересечения двух
плоскостей – прямая.
l:
11
Q2
A1 x B1 y C1 z D1 0 (Q1 )
A2 x B2 y C2 z D2 0 (Q2 )
(2)
Теорема.
Система уравнений (2) определяет
прямую в пространстве тогда и только
тогда, когда коэффициенты A1 , B1 , C1
не пропорциональны коэффициентам
2
A , B2 , C2
l
Система уравнений (2) называется общим уравнением прямой.
8. Аналитическая геометрия в пространстве.
2. Канонические уравнения прямой.
s m, n, p
M ( x, y, z )
l
Mo ( xo , yo , zo )
x xo y yo z zo
m
n
p
M ( x, y, z ) l.
MoM s MoM s
Пусть точка
Тогда
3. Параметрические уравнения прямой.
x xo
x xo m
m
y yo
y yo n
n
z zo
z z o p
p
x xo m
l : y yo n
z zo p
параметр
9. Аналитическая геометрия в пространстве.
Взаимное расположение плоскостей и прямых в пространстве.
1. Условие параллельности плоскостей.
n2 A2 , B2 , C2
Q2
Q1
Q1 : A1 x B1 y C1 z D1 0
Q2 : A2 x B2 y C2 z D2 0
Q1 Q2 n1 n2
A1 B1 C1
A2 B2 C2
n1 A1 , B1 , C1
2. Условие перпендикулярности плоскостей.
Q1
Q1 Q2 n1 n2
A1 A2 B1B2 C1C2 0
n2
n1
Q2
10. Аналитическая геометрия в пространстве.
3. Условие параллельности прямых.
s1 m1 , n1 , p1
l1
l2
l1 l2 s1 s2
s2 m2 , n2 , p2
l1
4. Условие перпендикулярности прямых.
l1 l2 s1 s2
m1 n1
p
1
m2 n2 p2
s1 m1 , n1 , p1
m1m2 n1n2 p1 p2 0
l2
s2 m2 , n2 , p2
11. Аналитическая геометрия в пространстве.
5. Условие параллельности прямой и плоскости.
n A, B, C
s m, n, p
l Q s n s n 0 Am Bn Cp 0
l
Q
6. Условие перпендикулярности прямой и плоскости.
s m, n, p
n A, B, C
l Q s n
Q
l
m n p
A B C








 mathematics
mathematics








