Similar presentations:
Анализ данных. Лекция 1. Основные понятия и определения теории вероятностей
1.
Анализ данных2.
Анализ данныхЛекция 1
Основные понятия и определения теории
вероятностей
3.
Основные понятия и определенияИспытание.
Под испытанием
или
опытом
понимается
осуществление определенного комплекса действий или
условий.
Проведение этого испытания в каких-либо других
условиях считается уже другим опытом.
4.
Основные понятия и определенияСобытие.
Каждое испытание заканчивается некоторым
результатом. Такие пезультаты будем называть
исходами или событиями.
Таким образом,
под событием понимается
явление, которое наступает в результате данного
испытания.
5.
Простейшие модели теории вероятностейПервая модель: «Монета»
Подбрасываем монету один раз.
Решка
Орел
или
6.
Простейшие модели теории вероятностейВторая модель: «Кубик»
Подбрасываем один раз игральную кость.
События:
«нечетное»
1
3
«четное»
5
2
3
4
6
«составное»
«простое»
1
2
5
4
6
7.
Классификация событийДостоверным
называют
обязательно произойдет
в
(Обозначается ).
событие,
которое
данном испытании.
Невозможным
называют
заведомо не произойдет в
(Обозначается ).
событие,
которое
данном испытании.
Случайным или возможным называют событие,
которое в данном испытании может произойти, либо не
произойти.
Случайные события обозначаются
латинскими буквами A, B, C, …
прописными
8.
Виды случайных событийЕсли при каждом испытании, при котором
происходит событие А, происходит и событие В, то
говорят, что А влечет за собой событие В (входит в В)
или В включает событие А и обозначают А В .
Диаграмма Венна
B
A
9.
Виды случайных событийПример. Событие А – выпадение 3, В – выпадение
нечетного числа, то А В
А = 3 ,
В = 1, 3, 5 .
Так как 3 1, 3, 5 А В.
10.
Виды случайных событийОпределение. Если одновременно А В и В
А, то в этом случае события А и В называются
равносильными.
Записывают А=В
Пример.
Монета: Выпал орел
Не выпала решка
=
Кубик:
Выпала «6»
=
Выпало более 5
11.
Виды случайных событийОпределение. Собы. тия А и В называются
несовместными (несовместимыми), если в
результате данного испытания появление
одного из них исключает появление другого.
В
А
Пример. Студент сдает экзамен по математике. В
этом испытании можно выделить следующие события:
A – студент сдал экзамен на «отлично»;
B – студент сдал экзамен на «хорошо»;
C – студент сдал экзамен на «удовлетворительно»;
D – студент сдал экзамен на «неудов.».
Очевидно, что все события несовместны, так как на
экзамене можно получить только одну оценку.
12.
Виды случайных событийОпределение. События А и В называются
совместными, если
в
результате
данного
испытания появление одного из них не исключает
появление другого.
А
В
Пример. Студент сдает экзамен по математике и
информатике. В этом испытании можно рассмотреть
следующие события:
A – студент сдал экзамен по математике;
B – студент сдал экзамен по информатике.
Очевидно, что эти события будут совместными, так
как студент может сдать оба экзамена.
13.
Виды случайных событийОпределение.
Несколько
событий
называются единственно возможными, если
в результате испытания одно из них
обязательно должно произойти.
Пример. В примере со студентом события A, B, C и
D - единственно возможные.
14.
Виды случайных событийОпределение.
События
называются
равновозможными, если есть основания считать,
что ни одно из этих событий не является более
возможным, чем другие.
орел
1
2
решка
3
4
5
6
15.
Виды случайных событийОпределение. Совокупность единственно
возможных несовместных
событий данного
испытания называют полной группой.
орел
решка
Полная группа
четное
нечетное
Полная группа
четное
простое
совместны
16.
Виды случайных событийОпределение.
Два события называются
противополож ными, если они составляют
полную группу событий.
Обозначение:
А
AиA
A
17.
Виды случайных событийМонета:
Орел
Кубик:
нечетное
2
Ω
Решка
четное
не выпала «2»
18.
Операции над событиями.1. Сумма событий.
Определение. Суммой (или объединением ) двух
событий A и B называется событие C, которое состоит в
том, что в результате опыта произошло хотя бы одно из
событий: либо A, либо B, либо и то и другое.
Обозначение: C A B
или
В
А
C A B
19.
Операции над событиями.1. Сумма событий.
Пример. Два студента сдают экзамен. Пусть
событие А – первый студент сдал экзамен, B – второй
студент сдал экзамен.
Сумма событий – хотя бы один студент сдал экзамен
Пример. Из колоды карт извлекают одну карту.
Пусть событие А – извлечена «дама», B – извлечена
карта пиковой масти.
Сумма событий – извлеченная карта будет либо
дамой, либо картой пиковой масти, либо дамой
пиковой масти
20.
Свойства операции объединения.1.Если одно событие A содержится в другом событии B,
то их объединение равно большему событию B.
A B B, если A B.
2.Достоверное событие, объединенное с любым
возможным событием, – это достоверное событие.
A , если A возможное событие.
21.
Свойства операции объединения3.Объединение противоположных событий – это
достоверное событие.
A A .
4.Объединение события A с самим собой равно этому же
событию A.
A A A.
22.
2. Произведение событийПересечением
Определение.
(или
событий A и B называется
произведением ) двух
событие C, которое состоит в том, что в результате
испытания наступает каждое из событий: и A, и B.
Обозначение:
C A B
В
А
23.
2. Произведение событийПример. Два студента сдают экзамен. Пусть
событие А – первый студент сдал экзамен, B – второй
студент сдал экзамен.
Произведение событий – оба студента сдали экзамен
Пример. Из колоды карт извлекают одну карту.
Пусть событие А – извлечена «дама», B – извлечена
карта пиковой масти.
Произведение событий – извлеченная карта будет
дамой пиковой масти.
24.
Свойства операции пересечения1.Если одно событие A содержится в другом событии B,
то их пересечение равно меньшему событию A.
A B A, если A B.
2.Пересечение несовместных событий – это невозможное
событие или
A B 0 , если A и B несовместны.
25.
Свойства операции пересечения3.Пересечение
противоположных
невозможное событие или
событий
–
это
A A 0 .
4.Пересечение
событию A.
события A с самим собой равно этому же
A A A.
26.
Свойства операции пересечения5. Пересечение двух событий A и B содержится в их
объединении.
( A B) ( A B).
27.
Пространство элементарных исходовОпределение. Полную группу событий, в которой
ни одно из событий не может быть представлено как
объединение более простых событий, будем называть
пространством элементарных исходов.
Определение. Элементы пространства элементарных
исходов называются элементарными событиями
(элементарными исходами).
Обозначения: Ω ─ пространство элементарных исходов,
1 , 2 ,... ─ элементарные исходы.
Монета:
Орел
Кубик:
1
Решка
2
3
4
5
6
28.
Пространство элементарных исходов.Свойства элементарных исходов.
1.
Элементарные
возможными.
исходы
являются
2.
Элементарные
несовместными.
исходы
являются
3.
Пространство
элементарных исходов в
каждом испытании единственное.
4.
Пространство элементарных исходов может
быть как конечным, так и бесконечным.
29.
Пространство элементарных исходов.Определение. Случайное событие называется
сложным , если оно является объединением
нескольких элементарных исходов.
Кубик:
четное
=
2
+ 4 + 6
30.
Статистическое и классическоеопределение вероятности события
Определение. Числовая характеристика,
показывающая
степень
объективной
возможности появления события называется
вероятностью данного события.
Вероятность
– это
наступления события.
мера
возможности
31.
Классическое определение вероятностиКлассическое
определение
вероятности
дает
возможность теоретического вычисления вероятности без
проведения эксперимента.
Пусть рассматриваемый эксперимент может иметь
конечное число (N ) равновозможных исходов, которые
составляют полную группу.
При этом в NA исходах (NA N) может наступить
интересующее нас событие A (благоприятные событию А
исходы).
Вероятность равна отношению числа благоприятных
исходов к общему числу всех равновозможных исходов, т.е.
NA
P A
N
32.
Классическое определениевероятности
Теорема. Вероятность сложного события равна
сумме вероятностей тех элементарных исходов, из
объединения которых оно состоит.
Кубик:
1
простое
2
3
5
P 1 P 2 P 3 P 5
P простое
1
6
1
6
1
6
1
6
1
6
4
6
2
3
33.
Свойства вероятностей1. Вероятность любого события неотрицательна и
не превосходит 1, т.е.:
0 P A 1
Доказательство.
Очевидно, что:
N 0,
0 N A N.
Разделим неравенство на N:
следовательно,
0 P A 1.
0 NA
N
,
N
N
N
34.
Свойства вероятностей2. Вероятность достоверного события равна 1.
P 1
Доказательство. N A N,
P( )
NA
N
N
1.
N
3. Вероятность невозможного события равна 0.
P 0
Доказательство. NA 0,
NA 0
P( ) 0.
N N
35.
Свойства вероятностей4. Сумма вероятностей событий, составляющих полную
группу, равна 1, т.е.:
n
P A 1.
i
i 1
Следствие 1. Сумма вероятностей противоположных
событий равна 1 , т.е.:
P A P A 1
Следствие 2. Вероятность противоположного события
определяется соотношением:
P A 1 P A
36.
Статистическое определениевероятности
Пусть произведена серия из N испытаний.
Предполагаем, что в NA испытаниях наступило
событие А.
Определение. Отношение числа появлений
события A к общему числу испытаний называется
относительной частотой или частостью события.
NA
w A
.
N
37.
Статистическое определениевероятности
Определение. Вероятность события A равна
пределу частости появления события A при
неограниченном увеличении числа испытаний, т.е.:
P A lim w(A).
N
38.
Статистическое определение вероятности.Условия применимости
1.Рассматриваемые события должны быть исходами
только
тех
испытаний,
которые
могут
быть
воспроизведены неограниченное число раз при одном
и том же комплексе условий.
2.События
должны
обладать
так
называемой
статистической устойчивостью, или устойчивостью
относительных частот.
3.Число испытаний, в результате которых появляется
событие А должно быть достаточно велико.
P( A) w( A)
39.
Геометрическое определение вероятностиПусть фигура g составляет часть фигуры G.
На фигуру G наудачу бросается точка.
Вероятность попадания брошенной точки на фигуру g
будет равна отношению меры (площади) фигуры g к мере
(площади) фигуры G.
g
G
Sg
P A .
SG
40.
Геометрическое определениевероятности
равна
Определение. Вероятность события A
отношению меры благоприятных исходов к мере общего
числа исходов.
mes A
P A
.
mes
41.
Геометрическое определениевероятности
Пример. В квадрат со стороной равной a вписан круг.
Найти вероятность того, что точка, брошенная в квадрат,
попадет в круг
Площадь квадрата равна:
SG a 2
Площадь круга, вписанного в
квадрат, равна:
Sg R
2
Вероятность будет равна:
a2
4
P A
2
a
/4
Sg
SG
a
2
4
.
42.
Спасибо за внимание43.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
44.
Анализ данныхЛекция 2
Основные теоремы теории
вероятностей
45.
Теорема сложения вероятностейДля любых двух несовместных событий A и B
вероятность суммы определяется аксиоматически
как сумма вероятностей этих событий, то есть:
P A B P A P B .
Для совместных событий A и B вероятность
суммы определяется на основании следующей
теоремы.
Теорема. Для любых двух событий A и B
вероятность наступления хотя бы одного из них
равна сумме их вероятностей без вероятности их
совместного наступления.
P A B P A P B P AB
46.
47.
48.
11/20 = 0,5549.
Теорема сложения вероятностейСледствие. Вероятность суммы трех событий
определяется соотношением:
P A B C P A P B P C
P AB P AC P BC P ABC .
50.
Условная вероятность событияОпределение.
Вероятность
события
В,
вычисленная в предположении, что событие А уже
наступило, называется условной вероятностью
события В.
Условная
соотношением:
вероятность
определяется
P AB
, P A 0.
PA B P B A
P A
51.
Условная вероятностьСвойства условных вероятностей
1) P B| P B .
2 ) Если A B, то P B| A 1.
3 ) P | A 0, если P A 0.
52.
Теорема умножения вероятностейТеорема. Вероятность совместного появления
двух событий равна произведению вероятности одного
из них на условную вероятность другого, вычисленную
в предположении, что первое событие уже наступило:
P( AB) P( A) P(B A)
53.
Теорема умножения вероятностейСледствие. Вероятность произведения нескольких
событий равна произведению вероятности одного из
этих событий на условные вероятности других; при
этом условная вероятность каждого последующего
события вычисляется в предположении, что все
предыдущие события произошли:
Например:
P( ABC) P( A) PA (B) PAB (C).
54.
Независимые событияОпределение. События A и B называются
независимыми, если вероятность появления одного
из них не меняется при наступлении другого, т.е.
P A | B P A .
В противном случае события A и B называются
зависимыми.
55.
Независимые события.Теорема умножения вероятностей для
независимых событий
Терема. Вероятность совместного наступления
двух независимых событий A и B равна произведению
их вероятностей, т.е.
P AB P A P(B).
56.
Свойства независимых событий1. Если события А и В имеют ненулевые вероятности, то
если событие A не зависит от события B, то и событие
B не зависит от события A.
Доказательство. Пусть
P A | B P A ,
P AB
P AB P A P B .
P A
P B
P AB P A P B
P B .
Рассмотрим P B | A
P A
P A
тогда
57.
Свойства независимых событий2. Если события A и B несовместны и их вероятности
отличны от нуля, то они зависимы.
Доказательство. P A 0 и P B 0.
События A и B несовместны, т.е.
Рассмотрим
P A| B
P AB 0.
P AB 0
P A ,
P B
следовательно, A и B зависимы.
Монета:
«Орел»
P(Орел) 0,5
«Решка»
P(Решка) 0,5
несовместны
зависимые
58.
Свойства независимых событий3. Если события А и В имеют ненулевые вероятности и
независимы, то независимы и события:
A и B,
A и B,
A и B.
59.
Независимые событияОпределение.
независимы ми в
События
называются
совокупности (или просто
независимыми),
если
наряду
с
их
попарной
независимостью наблюдается независимость любого из
них и произведения любого числа остальных событий.
В противном случае события называются
зависимыми.
Теорема. Вероятность
совместного появления
нескольких событий, независимых в совокупности,
равна произведению вероятностей этих событий, т.е.
P ABC P A P B P C
60.
Вероятность наступления хотя бы одногособытия
Замечание. В случаях трех и более совместных
событий соответствующая формула для вероятности
суммы весьма громоздка и проще переходить к
противоположному событию
Теорема.
Вероятность
суммы
нескольких
совместных событий (вероятность появления хотя бы
одного из них) равна разности между единицей и
вероятностью
произведения
противоположных
событий:
Р А1 А2 ... Аn 1 Р А1А2...An
61.
62.
63.
Формула полной вероятностиТеорема. Если событие F может произойти
только при условии появления одного из событий
(гипотез) H1, H2, … , Hn , образующих полную группу, то
вероятность события F равна сумме произведений
вероятностей каждого из этих событий (гипотез) на
соответствующие условные вероятности события F, то
есть:
P(F) P(H1)PH (F) P(H2 )PH (F) ... P(Hn )PH (F)
1
2
n
64.
Вероятность гипотез. Формула БайесаСледствием теоремы умножения и формулы
полной вероятности является формула Байеса. Она
применяется, когда событие F , которое может
появиться только с одной из гипотез H1, H2, … , Hn ,
образующих полную группу событий, произошло и
необходимо произвести количественную переоценку
априорных вероятностей гипотез, известных до
испытания, т.е. надо найти апостериорные условные
вероятности гипотез.
По теореме умножения имеем:
P(FHi ) P(Hi )PH(F)
i
Или
P(FHi ) P(F )PF(Hi)
65.
Вероятность гипотез. Формула БайесаОтсюда, приравнивая правые части и разрешая
относительно условной вероятности, получим:
P(Hi | F )
P(F | Hi ) P(Hi )
P(F )
Полученная формула называется формулой
Байеса (по имени английского математика, который их
вывел). Формулы Байеса позволяют переоценить
вероятности гипотез после того, как становится
известным результат испытания, в итоге которого
появилась событие F.
66.
Повторные независимые испытанияn – общее число испытаний
A – событие, которое мы считаем «успехом»
p P A
q P A 1 p
m – число успехов в последовательности из n
испытаний
67.
Повторные независимые испытанияТеорема. Если вероятность р наступления события А в
каждом испытании постоянна, то вероятность того, что
событие А наступит ровно m раз в n независимых
испытаниях, равна:
Pn,m Pn m C p q
m
n
m
n m
.
68.
Повторные независимые испытанияДоказательство. 1) Рассмотрим один благоприятный
исход,
например,
независимые
A
A
A
A
.
.
A
A
A
A
A
A
. .AAp p ... p q q ... q p q
Его вероятность:
m
n m
m
n m
m
n m
69.
Повторные независимые испытания2) Посчитаем количество благоприятных исходов.
Любой исход, в котором событие A встречается m раз,
является благоприятным:
AAAAA...AAA
Количество различных расстановок успехов
определяется числом сочетаний:
Таким образом,
C nm
Pn m C nm p m q n m .
Формула Бернулли
Ч.т.д.
70.
Применение формулы Бернулли при большихзначениях n затруднительно. Поэтому возникает
желание иметь более простые формулы для
вычисления вероятности при больших n. Такие
формулы называются асимптотическими.
71.
Если вероятность р наступлениясобытия А в каждом испытании стремится к нулю
(р 0) при неограниченном увеличении числа
испытаний (n ), причем произведение np стремится
к постоянному числу (np ), то вероятность Pm,n
того, что событие А появится m раз в n независимых
испытаниях, приближенно равна
Теорема.
.
Pm ,n Pm ( )
m e
m!
Условия применимости формулы Пуассона:
р – малая постоянная величина, n – достаточно
велико и = np – незначительно ( = np 10).
72.
Есливероятность р появления события А в каждом
испытании постоянна и отлична от нуля и единицы, то
вероятность Рm,n того, что событие А появится в n
независимых испытаниях ровно m раз, приближенно
равна
Локальная теорема Муавра-Лапласа.
Pm ,n
где
1
f(x) ,
npq
f(x)
x2
1
m np
2
.
e , x
npq
2
73.
Свойства функции Гаусса1. Функция Гаусса определена на всей числовой оси.
2. Функция является четной, то есть f(-x ) = f( x ),
3.Функция монотонно убывает при положительных
значениях х, а предел ee при х стремящимся к
бесконечности равен нулю.
4. Если аргумент функции больше 5, то можно считать,
0,5
очень
что f(x)=0, так как уже при х=5 ее значение
маленькое: f(5)= 0.0000015.
0,25
5. График функции Гаусса
0
-1,8
-1,2
-0,6
0
0,6
1,2
1,8
74.
Интегральнаятеорема
Муавра-Лапласа.
Если вероятность р появления события А в каждом
испытании постоянна и отлична от нуля и единицы,
то вероятность того, что число m наступления
события А в n независимых испытаниях заключено в
пределах от m1 до m2 (включительно),
при
достаточно большом числе n приближенно равна
Где
Лапласа,
Pn m1 m m2 Ф x2 Ф x1 ,
х
t2
1
2 dt
е
Ф( х )
2 0
функция
m np
x1 1
npq
m2 np
, x2
npq
75.
Свойства функции Лапласа1. Функция Ф( х ) определена на всей числовой оси.
2.Функция Ф( х ) - нечетная, т.е. Ф( -х ) = - Ф( х ).
3.Функция Ф( х ) - монотонно возрастающая на всей
области определения.
Предел функции при
х
стремящемся к плюс бесконечности равен 0,5.
4. Для всех значений аргумента, больших 5, можно
считать, что Ф(х) приблизительно равна 0,5.
76.
Повторные независимые испытанияСледствие из интегральной теоремы МуавраЛапласа.
Если вероятность р наступления события А в
каждом испытании постоянна и отлична от 0 и 1, то
при достаточно большом числе n независимых
испытаний вероятность того, что:
а) число m наступлений события А отличается от
произведения np не более, чем на положительную
величину (по абсолютной величине) определяется
соотношением:
Pn m np 2 Ф
;
npq
77.
Повторные независимые испытанияСледствие из интегральной теоремы МуавраЛапласа.
б) частость m/n события А заключена в
пределах от до (включительно) определяется
соотношением:
m
Pn Ф z 2 Ф z1 ,
n
где
p
z
,
1
pq / n
p
z
.
2
pq / n
78.
Повторные независимые испытанияСледствие из интегральной теоремы МуавраЛапласа.
в) частость m/n события А отличается от его
вероятности р не более, чем на положительную
величину (по абсолютной величине), определяется
соотношением:
n
m
Pn p 2 Ф
.
n
pq
79.
случайная величинаОпределение. Случайной величиной называется
переменная, которая в результате испытания принимает
то или иное числовое значение.
Пример. Число попаданий в мишень при выстрелах –
случайная величина.
Пример. Рост наудачу взятого человека – случайная
величина.
80.
Определение.Случайная
величина
называется
дискретной, если число ее возможных значений конечно или
счетно.
(множество называется счетным, если его элементы
можно перенумеровать натуральными числами.)
Определение.
Случайная
величина
называется
непрерывной, если она принимает возможные значения из
конечного или бесконечного промежутка.
В этом смысле, число попаданий в мишень – пример
дискретной случайной величины. Рост человека –
непрерывная случайная величина.
Для
обозначения
случайных
величин
будем
использовать буквы греческого алфавита (возможно с
индексами), например, (кси), (эта), (дзета) и т.п.
81.
Определение. Законом распределения дискретнойслучайной величины называется такая таблица, в которой
перечислены все возможные значения этой случайной
величины (без повторений) с соответствующими им
вероятностями.
В общем виде закон распределения для случайной
величины имеет вид:
где
x1
x2
…
xn
p
p1
p2
…
pn
pi P xi ,
82.
Закон распределения дискретной случайнойвеличины
основное свойство закона распределения
Из определения закона распределения следует, что
события ( = x1 ) ,
( = x2), … , ( = xn) образуют полную
систему, поэтому (см. следствие из теоремы сложения
вероятностей для несовместных событий ):
т.е.
P( x1) P( x2) ... P( xk) 1,
p 1 p 2 ... p k 1.
83.
Закон распределения дискретной случайнойвеличины
Пример. Два стрелка одновременно выстреливают в
мишень. Вероятность попадания для первого равна 0,6,
для второго – 0,8. Составить закон распределения
случайной величины – общего числа попаданий в
мишень.
Решение. Возможные значения данной случайной
величины : 0, 1, 2. Обозначим события, состоящие в
попадании в мишень первого и второго стрелков через В1
и В2, соответственно.
P( 0) P(B1B2) P(B1)P(B2) (1 0,6) (1 0,8) 0, 4 0, 2 0,08;
P( 1) P(B1B2 B1B2) P(B1)P(B2) P(B1)P(B2) 0,6 0,2 0,4 0,8 0,44,
P( 2) P(B1B2 ) P(B1)P(B2 ) 0,6 0,8 0,48.
84.
Закон распределения дискретной случайной величиныОкончательно,
величины имеет вид:
закон
распределения
0
1
2
p
0,08
0,44
0,48
1
случайной
85.
Спасибо за внимание86.
Анализ данныхЛекция 3
Случайные величины, их законы
распределения.
87.
Арифметические операции над случайнымивеличинами
Пусть случайная величина и имеют следующие
законы распределения:
x1
x2
…
xn
y1
y2
…
ym
p
p1
p2
…
pn
p
p1
p2
…
pm
88.
Арифметические операции над случайными величинами1. Произведение сл.в. на постоянную величину С -это новая сл.в. С , которая с теми же вероятностями, что и
сл.в. принимает значения, равные, произведениям реализаций
сл.в. на С.
Следовательно, ее закон распределения будет иметь вид:
С
Сx1
Сx2
…
Сxn
p
p1
p2
…
pn
89.
Арифметические операции над случайными величинами2. Квадрат сл.в. , т.е. 2 - это новая сл.в., которая с
теми же вероятностями, что и принимает значения,
равные квадратам ее значений.
Ее закон распределения:
2
x1 2
x2 2
…
xn 2
p
p1
p2
…
pn
90.
Арифметические операции над случайнымивеличинами
3. Сумма сл.в. и - это новая сл.в., которая
принимает все значения вида xi+yj с вероятностями pij,
выражающими вероятность того, что сл.в. примет
значение xi, а - значение yj, т.е.
pij= P( =xi, =yj) = P( =xi)P( =yj| =xi).
Определение. Случайные величины и называются
независимыми, если для любых i
и j события ( = хi) и
( = yj )– независимы.
Если сл.в. и независимы, то
pij = P( =xi, =yj) = P( =xi)P( =yj)
91.
Числовые характеристики дискретной случайнойвеличины.
Математическое ожидание
Определение.
Математическим
ожиданием
дискретной случайной величины называется число М ,
вычисляемое по формуле
n
M xi pi x1 p1 x2 p2 ... xn pn .
i 1
92.
Свойства математического ожиданияМатематическое ожидание случайной величины есть
число около которого группируются значения этой случайной
величины.
1.Математическое ожидание постоянной случайной
величины равно самой постоянной, т.е.
М(С)=С,
где С – некоторое число.
2. Постоянный множитель можно выносить за знак
математического ожидания, т.е.
где – произвольное число.
M ( ) M ( ),
93.
Математическое ожиданиеСвойства математического ожидания
3.
Математическое
ожидание
суммы
(разности)
случайных величин равно сумме (разности) математических
ожиданий этих случайных величин, т.е.
M ( ) M ( ) M ( ).
4.
Математическое ожидание произведения независимых
случайных величин равно произведению их математических
ожиданий, т.е.
M ( ) M ( )M ( ).
94.
Дисперсия дискретной случайнойвеличины
Математическое
достаточной степени
величину.
ожидание
не
характеризовать
может
в
случайную
При одном и том же математическом ожидании
случайные величины могут существенно различаться.
Различие можно характеризовать степенью
отклонения
случайной
величины
от
ее
математического ожидания.
В
качестве
такой
характеристики
рассматривается дисперсия случайной величины.
Слово дисперсия означает "рассеяние".
95.
Дисперсия дискретной случайнойвеличины
Дисперсией D( ) случайной
величины Х называется математическое ожидание
квадрата ее отклонения от математического ожидания:
Определение.
D( ) M [ M ( )]2
Если случайная величина Х – дискретная с конечным
числом значений, то
n
D( ) (xi a) 2 pi .
i 1
96.
Дисперсия дискретной случайнойвеличины
Дисперсия D имеет размерность квадрата
случайной величины. Поэтому в качестве показателя
рассеяния используют также величину
D
Средним квадратическим
отклонением)
отклонением
(стандартным
случайной величины называется арифметическое
Определение.
значение корня квадратного из ее дисперсии:
D .
97.
Дисперсия дискретной случайнойвеличины. Свойства дисперсии.
1. Дисперсия постоянной величины равна нулю:
D( C ) 0.
Доказательство.
D( C ) M [ C M ( C )] 2 M ( C C )2 M ( 0 ) 0.
2.
Постоянный
множитель можно выносить за
знак дисперсии, возведя его при этом в квадрат:
D(k ) k 2 D
Доказательство.
D(k ) M [k M (k )]2 M (k kM )2
k 2 M ( M )2 k 2 D .
98.
Дисперсия дискретной случайнойвеличины. Свойства дисперсии.
Дисперсия случайной величины равна
разности между математическим ожиданием квадрата
случайной величины и квадратом ее математического
ожидания:
D M ( 2 ) [M ]2
3.
Доказательство.
Учитывая, что М – величина постоянная,
получим:
D M ( M ) 2 M ( 2 2 M M 2 )
M 2 2 M M M 2
M 2 M 2 .
99.
Дисперсия дискретной случайнойвеличины. Свойства дисперсии.
Дисперсия
суммы
(разности)
двух
независимых случайных величин равна суммеих
дисперсий: D( ) D( ) D( ) .
4.
Доказательство. По свойству 3:
D( ) M ( ) 2 [ M ( )] 2
величин
M ( 2 2 2 ) [ M M ]2
Учитывая, что для независимых случайных
получим:
M ( ) M M
D( ) M 2 2M M M 2
M 2 2 M M M 2
( M 2 M 2 ) ( M 2 M 2 ) D D .
100.
Основные законы распределения дискретнойслучайной величины.
Биномиальный закон распределения
Случайная величина имеет
биномиальны й
закон
распределения
с
параметрами n и p, если она принимает значения 0,
1, 2, …, n c вероятностями Pm,n вычисляемыми по
формуле Бернулли:
Определение.
P
m ,n
C
m
n
m
p q
n m
,
101.
Биномиальный закон распределенияМатематическое ожидание случайной
величины , распределенной по биномиальному закону,
Теорема.
а ее дисперсия
M np ,
D npq .
Доказательство. Представим случайную величину
– число m наступлений события А в n независимых
испытаниях
–
в
виде
суммы
n одинаково
распределенных независимых случайных величин к ,
где к =1,2, … , n, а к – случайная величина,
выражающая число наступлений события А в к-ом
испытании.
n
k
k 1
102.
Биномиальный закон распределенияСлучайная величина к имеет следующий закон
распределения Бернулли:
i
0
1
pi
q
p
Найдем
числовые
х арактеристики
случайной
величины к :
M 0 q 1 p p ,
k
D k (0 p) 2 q (1 p) 2 p
p2 q q2 p pq( p q) pq ,
103.
Биномиальный закон распределенияТак как математическое ожидание и дисперсия
суммы независимых случайных величин равны сумме их
математических ожиданий и дисперсий, получим:
M M ( 1 2 ... n ) p p ... p np ,
D D( 1 2 ... n ) pq pq ... pq npq .
104.
Биномиальный закон распределенияСледствие. Математическое ожидание
частости
m/n наступления события A в n независимых
испытаниях, в каждом из которых оно может наступить
с одной и той же вероятность р, равно р, т.е.:
а ее дисперсия
m
M p ,
n
m pq
D
.
n n
105.
Биномиальный закон распределенияДоказательство. Частость события m/n есть
случайная величина вида /n, где – случайная
величина, распределенная по биномиальному закону.
Поэтому
m
1
1
M M M np p ,
n
n
n n
m
1
1
pq
D D 2 D 2 npq
.
n
n
n
n n
106.
Закон распределения ПуассонаВ пределе при n и np = биномиальное
называемое
распределение
переходит
в
так
распределение Пуассона.
Определение. Говорят, что случайная величина
имеет распределение Пуассона с параметром ,
если она принимает значения
0, 1, 2, …
c
вероятностями
Pm
вычисляемыми по формуле
Пуассона:
m
Pm
e
m!
где m = 0, 1, 2, 3, … , – положительное
целое число.
107.
Закон распределения ПуассонаУбедимся в том, что для распределения Пуассона
выполняется основное свойство закона распределения:
Pm 1
Действительно, mи м0еем
2 3
e e e e ... 1 ... e e e 1
Pm
m 0
0!
1!
2!
3!
2! 3!
0 1 2 3
Теорема. Математическое ожидание и дисперсия
случайной величины , распределенной по закону
Пуассона, совпадают и равны параметру этого
закона, т.е.
M ,
D .
108.
Геометрическое распределениеОдно и тоже испытание проводится до первого
успеха. В каждом испытании вероятность наступления
успеха одинакова и равна р.
Определение. Случайная величина имеет
геометрический
закон
распределения
с
параметром p, если она принимает значения 1, 2, …,
c вероятностями, вычисляемыми по формуле:
P m pq m 1
Математическое ожидание и дисперсия :
1
M ,
p
q
D 2 .
p
109.
Случайный векторОчень часто результат испытания характеризуется
не одной случайной величиной, а некоторой системой
случайных величин 1, 2, …, n, которую называют
также многомерной (n-мерной) случайной величиной
или случайным вектором = ( 1, 2, …, n ).
Случайные величины, входящие в систему, могут
быть как дискретными, так и непрерывными.
Определение. Вектор = ( , ), компоненты и
которого являются случайными величинами,
называется случайным вектором или
двумерной случайной величиной.
110.
Закон распределения111.
Закон распределенияПример
1. Совместный закон
случайных величин и имеет вид:
Найти
законы
случайных величин.
распределения
распределения
одномерных
112.
Условные законы распределенияОпределение. Закон распределения одной из
переменных при фиксированном значении другой
называется условны мраспределением.
Вероятности рj(xi) этого распределения будут
условными вероятностями события = хi, найденными
в предположении, что событие =yj произошло.
113.
Условные законы распределенияПример
2. Найти условные распределения
случайных величин, совместный закон распределения
которых представлен в примере 1.
114.
Условные законы распределенияАналогично можно определить условные
распределения для случайной величины .
законы
Используя соответствующие законы распределения,
для одномерных составляющих случайных величин и
можно определить числовые характеристики –
математические ожидания М , М и дисперсии D и D ,
а также условные математические ожидания М ,
М
и условные дисперсии D и D , которые
рассмотренным
находятся по обычным формулам,
ранее.
115.
Условные законы распределенияОпределение.
Связь
между
переменными
называется
функциональной,
если
каждому
значению из области определения одной переменной
поставлено в соответствие однозначно определенное
значение другой переменной.
Определение. Функциональная связь между
значениями
одной
переменной
и
условными
математическими ожиданиями другой переменной
называется корреляционной.
Определение.
График
корреляционной
зависимости называется линией регрессии.
Корреляционные зависимости бывают двух видов y
по x и x по y в зависимости от того, которая из
переменных выполняет роль аргумента: x или y.
Соответственно, – точки корреляционной зависимости
y по x и – точки корреляционной зависимости x по y.
116.
Условные законы распределенияПример 3. По совместному закону распределения
из предыдущего примера
зависимость y по x и x по y.
найти
xi
1
2
M x
23
47
M y
74
53
yj
0
1
i
j
корреляционную
117.
Ковариация и ее свойстваКовариацией
корреляционны м
(или
моментом ) случайных величин и называется
математическое ожидание произведения отклонения
этих величин от своих математических ожиданий, т.е.
118.
Ковариация и ее свойстваСвойства ковариации:
1. Ковариация двух
величин равна нулю.
независимых
случайных
119.
Ковариация и ее свойства2. Ковариация двух случайных величин равна
математическому ожиданию их произведения минус
произведение их математических ожиданий, т.е.
120.
Ковариация и ее свойстваКовариация двух случайных величин по
абсолютной величине не превосходит произведения их
средних квадратических отклонений, т.е.
3.
121.
Ковариация и ее свойства4. Дисперсия суммы (разности) двух случайных
величин равна сумме их дисперсий плюс (минус)
удвоенная ковариация:
D( ) D( ) D( ) 2 K , .
122.
Коэффициент корреляции и егосвойства
Определение. Коэффициентом корреляции
случайных величин и называется число,
определяемое равенством
123.
Коэффициент корреляции и егосвойства
1. Коэффициент
корреляции не превосходит по
абсолютной величине единицы, т.е.
124.
Коэффициент корреляции и егосвойства
2. Если случайные величины независимы, то их
коэффициент корреляции равен нулю, т.е.
125.
Коэффициент корреляции и егосвойства
3. Если модуль коэффициента корреляции двух
случайных величин равен 1, то между этими
случайными
величинами
существует
линейная
функциональная зависимость.
126.
Функция распределения случайнойвеличины.
В качестве
описания дискретной случайной
величины
ранее
рассматривали
закон
ее
распределения. Однако такое описание не является
единственным, а, главное, не универсально. Так, оно
неприменимо для описания непрерывной случайной
величины.
Для описания закона распределения случайной
величины возможен следующий подход: рассматривать
не вероятность события { =х} для разных значений х
(как это имеет место в законе распределения), а
вероятности события { <x} , где х – текущая
переменная. Вероятность P( <x), очевидно, зависит от
х, т.е. является некоторой функцией от х.
127.
Функция распределения случайнойвеличины.
Функцией распределения
случайной величины
называется функция F(x),
выражающая для каждого значения х вероятность того,
что случайная величина примет значение меньшее х:
Определение.
F (x) P( x) .
Геометрически
функция
распределения
интерпретируется как вероятность того, что случайная
точка попадет левее заданной точки х.
<x
0
x
x
128.
Свойства функции распределенияслучайной величины.
1.Функция распределения случайной величины есть
неотрицательная функция, заключенная между нулем и
единицей:
0 F( x ) 1.
Это
утверждение следует из того, что функция
распределения – это вероятность.
129.
Свойства функции распределенияслучайной величины.
2. Функция распределения случайной величины
есть неубывающая функция на всей числовой оси.
имеем:
По теореме сложения несовместных событий,
или
P( x 2) P( x 1) P(x 1 x )2
F (x2 ) F (x1) P(x1 x2 ).
Так как вероятность
P(x1 x2 ) 0,
то F(x2) F(x1) , т.е. F(x) -- неубывающая
функция.
130.
Свойства функции распределения случайнойвеличины.
3. На минус бесконечности функция распределения
равна нулю, а на плюс бесконечности равна единице,
т.е.
F ( ) xlim
F (x) 0 ,
Событие
следовательно,
<–
F ( ) lim F ( x ) 1 .
является
x
невозможным,
F( ) P(X ) 0.
Событие < + . Является достоверным событием,
следовательно,
F( ) P( X ) 1 .
131.
Свойства функции распределения случайнойвеличины.
4. Вероятность попадания случайной величины в
интервал [x1 , x2 ) равна приращению ее функции
распределения на этом интервале, т.е.
P(x1 x2 ) F (x2 ) F (x 1 ).
Это формула непосредственно следует из свойства
2. Действительно:
Отсюда,
F (x2 ) F (x1) P(x1 x2 ).
выражая
вероятность,
необходимое соотношение.
получим
132.
Непрерывные случайные величины.Определение. Случайная величина называется
непрерывной, если ее функция распределения
непрерывна в любой точке и дифференцируема всюду,
кроме, быть может, отдельных точек.
Теорема. Вероятность любого отдельно взятого
значения непрерывной случайной величины равна
нулю, т.е.
P x1 0.
Покажем, что для любого значения х1 случайной
величины вероятность Р( =х1) = 0 . Представим
Р( =х1) в виде
P x1 lim P x1 x2
x2 x1
133.
Непрерывные случайные величины.Применяя свойство 4 функции распределения
случайной величины и учитывая непрерывность F(x),
получим:
lim F x2 F x1 lim F x2 F x1
x2 x1
x2 x1
F x1 F x1 0.
134.
Непрерывные случайные величины.Следствие. Если -- непрерывная случайная
величина, то вероятность попадания случайной
величины в интервал (х1, х2) не зависит от того,
является этот интервал открытым или закрытым, т.е.
P x1 x 2 P x1 x 2
P x 1 x 2 P x 1 x 2 .
Действительно,
согласно теореме о вероятности
суммы несовместных событий, имеем:
0
P x1 x 2 P x1
P x1 x 2 P x 2
0
P x1 x 2 .
Аналогично доказываются и другие равенства.
135.
Непрерывные случайные величины.Плотность вероятности.
Плотностью
вероятности
(плотностью
распределения
или
просто
плотностью) (х) непрерывной случайной величины
Х называется производная ее функции распределения
Определение.
(x) F (x) .
График плотности вероятности называется кривой
распределения.
136.
Свойства плотности вероятности1.
Плотность
функция, т.е.
вероятности
–
неотрицательная
( х ) 0 .
Доказательство.
По определению функция плотности вероятности
есть производная от монотонно неубывающей функции
распределения.
Следовательно,
ее
производная
неотрицательная.
137.
Свойства плотности вероятности2. Вероятность попадания непрерывной случайной
величины в интервал [a;b] равна определенному
интегралу от ее плотности вероятности в пределах от а
b
до в, т.е.
P(a b) (x)dx .
a
Доказательство.
Согласно свойству 4 функции распределения
P(a b) F(b) F(a).
Так как функция F(x) есть первообразная для
функции плотности вероятности, то по формуле
Ньютона-Лейбница приращение первообразной на
отрезке [a;b] есть определенный интеграл от функции
плотности в пределах от а до в.
138.
Свойства плотности вероятностиИз последнего свойства следует геометрический
смысл функции плотности. Вероятность того, что
непрерывная случайная величина примет значение из
[a;b]
равна
площади
фигуры,
промежутка
ограниченной
сверху
кривой
распределения
и
опирающейся на отрезок [a;b].
(x)
S=P(a b)
0
a
b
x
139.
Свойства плотности вероятности3. Функция распределения непрерывной случайной
величины может быть выражена через плотность
вероятности по формуле:
x
F ( x ) ( x )dx .
Эта формула получается из предыдущей (свойство
2) при а - , если верхний предел в заменить на
переменный предел х.
140.
Свойства плотности вероятностиНесобственный
интеграл в бесконечных
пределах от плотности вероятности непрерывной
случайной величины равен единице:
4.
( x )dx 1 .
Доказательство.
распределения
Согласно
свойству
функции
F ( ) 1 .
получим:
x
( x )dx lim ( x )dx lim F ( x )
x
F ( ) 1 .
x
141.
Математическое ожидание и дисперсия непрерывнойслучайной величины.
M x (x)dx ,
D (x a) 2 (x)dx .
На практике обычно область значений случайной
величины, для которых (x) # 0, ограничена и
указанные интегралы сходятся, а значит, существуют
М и D .
Если функция плотности отлична от нуля только на
промежутке от а до в, то формулы принимают вид:
в
M x (x)dx ,
а
в
D (x a) 2 (x)dx .
а
142.
Математическое ожидание и дисперсия непрерывнойслучайной величины.
Все
свойства
математического
ожидания
и
дисперсии, рассмотренные выше для дискретных
случайных величин, справедливы и для непрерывных
случайных величин.
В частности, для дисперсии справедлива терема:
или
D M 2 M 2 ,
D
x (x)dx M .
2
2
143.
Спасибо за внимание144.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
145.
Анализ данныхЛекция 4
Непрерывные случайные величины
146.
Функция распределения случайнойвеличины.
Функцией распределения
случайной величины
называется функция F(x),
выражающая для каждого значения х вероятность того,
что случайная величина примет значение меньшее х:
Определение.
F (x) P( x) .
Геометрически
функция
распределения
интерпретируется как вероятность того, что случайная
точка попадет левее заданной точки х.
<x
0
x
x
147.
Свойства функции распределенияслучайной величины.
1.Функция распределения случайной величины есть
неотрицательная функция, заключенная между нулем и
единицей:
0 F( x ) 1.
Это
утверждение следует из того, что функция
распределения – это вероятность.
148.
Свойства функции распределенияслучайной величины.
2. Функция распределения случайной величины
есть неубывающая функция на всей числовой оси.
имеем:
По теореме сложения несовместных событий,
или
P( x 2) P( x 1) P(x 1 x )2
F (x2 ) F (x1) P(x1 x2 ).
Так как вероятность
P(x1 x2 ) 0,
то F(x2) F(x1) , т.е. F(x) -- неубывающая
функция.
149.
Свойства функции распределения случайнойвеличины.
3. На минус бесконечности функция распределения
равна нулю, а на плюс бесконечности равна единице,
т.е.
F ( ) xlim
F (x) 0 ,
Событие
следовательно,
<–
F ( ) lim F ( x ) 1 .
является
x
невозможным,
F( ) P(X ) 0.
Событие < + . Является достоверным событием,
следовательно,
F( ) P( ) 1.
150.
Свойства функции распределения случайнойвеличины.
4. Вероятность попадания случайной величины в
интервал [x1 , x2 ) равна приращению ее функции
распределения на этом интервале, т.е.
P(x1 x2 ) F (x2 ) F (x 1 ).
Это формула непосредственно следует из свойства
2. Действительно:
Отсюда,
F (x2 ) F (x1) P(x1 x2 ).
выражая
вероятность,
необходимое соотношение.
получим
151.
Непрерывные случайные величины.Определение. Случайная величина называется
непреры вной, если ее функция распределения
непрерывна в любой точке и дифференцируема всюду,
кроме, быть может, отдельных точек.
Теорема. Вероятность любого отдельно взятого
значения непрерывной случайной величины равна
нулю.
P x1 lim P x1 x2 .
x2 x1
Покажем, что для любого значения х1 случайной
величины вероятность Р( =х1) = 0 . Представим
Р( =х1) в виде
P x1 lim P x1 x2
x2 x1
152.
Непрерывные случайные величины.Применяя свойство 4 функции распределения
случайной величины и учитывая непрерывность F(x),
получим:
lim F x2 F x1 lim F x2 F x1
x2 x1
x2 x1
F x1 F x1 0.
153.
Непрерывные случайные величины.Следствие. Если -- непрерывная случайная
величина, то вероятность попадания случайной
величины в интервал (х1, х2) не зависит от того,
является этот интервал открытым или закрытым, т.е.
P x1 x 2 P x1 x 2
P x 1 x 2 P x 1 x 2 .
Действительно,
согласно теореме о вероятности
суммы несовместных событий, имеем:
0
P x1 x 2 P x1
P x1 x 2 P x 2
0
P x1 x 2 .
Аналогично доказываются и другие равенства.
154.
Непрерывные случайные величины.Плотность вероятности.
Плотностью
вероятности
(плотностью
распределения
или
просто
плотностью ) (х ) непрерывной случайной величины
называется производная ее функции распределения
Определение.
(x) F (x) .
График плотности вероятности называется кривой
распределения.
155.
Свойства плотности вероятности1.
Плотность
функция, т.е.
вероятности
–
неотрицательная
( х ) 0 .
Доказательство.
По определению функция плотности вероятности
есть производная от монотонно неубывающей функции
распределения.
Следовательно,
ее
производная
неотрицательная.
156.
Свойства плотности вероятности2. Вероятность попадания непрерывной случайной
величины в интервал [a;b] равна определенному
интегралу от ее плотности вероятности в пределах от а
b
до в, т.е.
P(a b) (x)dx .
a
Доказательство.
Согласно свойству 4 функции распределения
P(a b) F(b) F(a).
Так как функция F(x) есть первообразная для
функции плотности вероятности, то по формуле
Ньютона-Лейбница приращение первообразной на
отрезке [a;b] есть определенный интеграл от функции
плотности в пределах от а до в.
157.
Свойства плотности вероятностиИз последнего свойства следует геометрический
смысл функции плотности. Вероятность того, что
непрерывная случайная величина примет значение из
[a;b]
равна
площади
фигуры,
промежутка
ограниченной
сверху
кривой
распределения
и
опирающейся на отрезок [a;b].
(x)
S=P(a X b)
0
a
b
x
158.
Свойства плотности вероятности3. Функция распределения непрерывной случайной
величины может быть выражена через плотность
вероятности по формуле:
x
F ( x ) ( x )dx .
Эта формула получается из предыдущей (свойство
2) при а - , если верхний предел в заменить на
переменный предел х.
159.
Свойства плотности вероятностиНесобственный
интеграл в бесконечных
пределах от плотности вероятности непрерывной
случайной величины равен единице:
4.
( x )dx 1 .
Доказательство.
распределения
Согласно
свойству
функции
F ( ) 1 .
получим:
x
( x )dx lim ( x )dx lim F ( x )
x
F ( ) 1 .
x
160.
Математическое ожидание и дисперсия непрерывнойслучайной величины.
M x (x)dx ,
D (x a) 2 (x)dx .
На практике обычно область значений случайной
(x)≠0, ограничена и
величины, для которых
указанные интегралы сходятся, а значит, существуют
М и D .
Если функция плотности отлична от нуля только на
промежутке от а до в, то формулы принимают вид:
в
M x (x)dx ,
а
в
D (x a) 2 (x)dx .
а
161.
Математическое ожидание и дисперсия непрерывнойслучайной величины.
Все
свойства
математического
ожидания
и
дисперсии, рассмотренные выше для дискретных
случайных величин, справедливы и для непрерывных
случайных величин.
В частности, для дисперсии справедлива терема:
или
D M 2 M 2 ,
D
x (x)dx M .
2
2
162.
Равномерный закон распределения.Определение. Непрерывная случайная величина
имеет равномерны й закон распределения на
отрезке [a , b ], если ее плотность вероятности (х)
постоянна на этом отрезке и равна нулю вне его, т.е.
1
a x b,
( х ) b a при
0
при x a, x b.
у
1/(b-a)
S=1
0
a
b
х
163.
Равномерный закон распределения.Функция распределения случайной
величины , распределенной по равномерному закону,
при x a,
0
есть
Теорема.
x a
F( x )
при a x b,
b a
при x b.
a b
1
M
ее математическое ожидание
2
2
(b
a)
дисперсия D
.
12 у
,
1
0
a
b
х
164.
Равномерный закон распределенияПример.
Плотность
величины имеет вид:
0
1
(x)
04
при
вероятности
случайной
x 1,
при 1 x b,
при
x b.
Найти: а) параметр b;
б) математическое ожидание и дисперсию
в) функцию распределения F(x) и построить ее
график.
165.
Равномерный закон распределения0
1
(x)
04
при
x 1,
у
при 1 x b, 1/4
при
x b.
S=1
1
S b 1 1,
4
b 5.
1
b
х
5
5
2 5
1
1
1 2 2
1 x
M x x dx x dx xdx
5 1 3.
4
41
8
4 21
1
D M ( 2 ) [M ]2 5
3
5
5
1
124 31
x
1
1 2
3
3
2
2
2 1
5 1
M x x dx x dx x dx
12
3
4 3 1 12
4
41
1
31
31 27 4
D 32
1,333. D 4 2 1,155.
3
3
3
3
3
0
166.
Равномерный закон распределенияФункция распределения
непрерывной случайной
x
величины
F x t dt.
x 1:
x
x
F x t dt 0dt 0 ;
x
1
x
1
1
1
1 x 5:
F x t dt 0dt dt t x 1 ;
4 1 54
4
1 4
x
5
x
1
1
x 5 : F x t dt 0dt dt 0dt 1 t 1 5 1 1.
4
4 1 4
5
4
у1
0, при x 1,
1
1
F x x 1 , при 1 x 5,
4
1, при x 5.
0
x
1
b
х
167.
Показательный или экспоненциальный законраспределения
Определение. Непрерывная случайная величина
имеет показательны й или экспоненциальны й
закон распределения с параметром , если ее
функция распределения и плотность распределения
имеют вид:
при x 0,
при x 0,
0,
0,
F( x )
( x ) x
x
, при x 0.
e
,
при
x
0.
1
e
M D
1
.
168.
Показательный или экспоненциальный законраспределения
Пример. Электронное устройство выходит из строя
после 10000 часов работы с вероятностью 0,4. Считая,
что время непрерывной работы распределено по
показательному
закону,
определить
параметр
распределения, записать функции распределения и
плотности распределения, вычислить математическое
P x F( x )
ожидание и дисперсию.
P 10000 1 P 10000
Решение.
1 F (10000 ) 1 1 e 10000 e 10000 0,4.
10000 lne ln0,4.
lne 10000 ln0,4.
10000 0,916. 0,916 0,0000916.
1 10000 1
M D
10917.
0,0000916
D 109172 119180889.
169.
0,при x 0,
0 ,0000916 x
, при x 0.
0,0000916e
( x )
при x 0,
0,
F( x )
0 ,0000916 x
, при x 0.
1 e
Определить вероятность того, что выбранное
электронное устройство проработает:
А) не более 5000 час.;
Б) от 4000 до 8000час.
P x F( x )
P 5000 F( 5000 ) 1 e 0 ,0000916 5000
1 e 0 ,458 1 0,633 0,367.
P x1 x2 F( x2 ) F( x1 )
P 4000 8000 F( 8000 ) F( 4000 )
1 e 0 ,0000916 8000 1 e 0 ,0000916 8000
1 e 0 ,7328 1 e 0 ,3664 0,6932 0,4806 0,2126.
170.
Спасибо за внимание171.
Анализ данныхЛекция 5
Нормальный закон распределения.
Предельные теоремы теории вероятностей.
Закон больших чисел.
172.
Нормальный закон распределенияОпределение. Непрерывная случайная величина
имеет нормальны й закон распределения (закон
Гаусса) с параметрами a и 2, если ее плотность
распределения имеет вид:
1
e
N ( x)
2
( x a )2
2 2
.
173.
Нормальный закон распределенияКривую
нормального
закона
распределения
называют нормальной или гауссовой кривой.
(x)
0
a
x
Нормальная кривая симметрична относительно
прямой х = a , имеет максимум в точке х = a.
174.
Нормальный закон распределенияМатематическое ожидание случайной
величины , распределенной по нормальному закону,
равно параметру a этого закона, т.е.
Теорема.
M a,
а ее дисперсия – параметру 2 , т.е.
D 2.
175.
Нормальный закон распределенияДоказательство.
случайной величины :
Математическое
1
M x N (x)dx x
e
2
( x a) 2
2 2
dx.
t
x a
.
2
меняются
и,
Произведем замену переменной, положив
Тогда
x a 2t
dx 2dt.
Пределы
интегрирования
следовательно,
не
ожидание
176.
Нормальный закон распределения1 (a 2t)e 2dt
M
2
t
2
a
2 t
t
te
dt
e
dt
2
2
Первый интеграл равен нулю как интеграл от
нечетной функции по симметричному относительно
начала координат промежутку, а второй интеграл –
интеграл Эйлера-Пуассона равен
Таким образом:
0
a
a.
177.
Нормальный закон распределенияВыясним, как будет меняться нормальная кривая
при изменении параметров a и 2 . Если = const, и
меняется
параметр
a,
т.е.
центр
симметрии
распределения, то нормальная кривая будет смещаться
вдоль оси абсцисс, не меняя формы.
(х)
0
а 1 < a 2 < a3
а1
а2
а3
х
178.
Если a = const, и меняется параметр 2, то меняетсяордината максимума. При увеличении ордината
максимума кривой уменьшается, но так как площадь под
любой кривой распределения должна оставаться равной
единице, то кривая становится более плоской ,
растягиваясь вдоль оси абсцисс; при уменьшении ,
напротив, нормальная кривая вытягивается вверх,
одновременно сжимаясь с боков.
(х
)
1
1 < 2 < 3
2
3
0
а
х
179.
Нормальный закон распределенияТаким
образом,
параметр
a
характеризует
положение, а параметр 2 – форму нормальной кривой.
Нормальный закон распределения случайной
величины с параметрами a = 0, 2 = 1 , т.е. N(0,1),
называется стандартным или нормированным, а
соответствующая нормальная кривая – стандартной или
нормированной.
180.
Функция распределения нормальной случайнойвеличины
Функция распределения случайной
величины , распределенной по нормальному закону,
выражается через функцию Лапласа Ф(х) по формуле:
1
x a
FN (х) Ф
.
22
где
Теорема.
x
t
1
2 dt
Ф(х)
e
2 0
-- функция Лапласа,
рассмотрены ранее.
свойства
которой
были
181.
Свойства случайной величины, распределенной понормальному закону.
1. Вероятность попадания случайной величины,
распределенной по нормальному закону, в интервал
[x1 , x2 ], равна
P(x1 x2 ) Ф(t2 ) Ф(t1),
где
t1
x1 a
,
t2
x2 a
.
182.
Свойства случайной величины, распределенной понормальному закону.
2. Вероятность того, что отклонение
случайной
величины , распределенной по нормальному закону,
от математического ожидания а не превысит величину
> 0 (по абсолютной величине), равна
где
P( a ) 2Ф(t),
t
.
183.
Свойства случайной величины, распределенной понормальному закону.
Вычислим по последней формуле
вероятности при различных значениях .
некоторые
P( a ) Ф(1) 0,6827;
2
P( a 2 ) Ф(2) 0,9545;
3
P( a 3 ) Ф(3) 0,9973.
Отсюда вытекает "правило трех сигм":
Если случайная величина имеет нормальный
закон распределения с параметрами a и 2,
т.е. N(a , 2 ), то практически достоверно, что ее
значения заключены в инте рвале
а 3 , а 3 .
184.
Неравенство Маркова (лемма Чебы шева)Если случайная величина принимает только
неотрицательные значения и имеет математическое ожидание, то для
любого положительного числа А верны неравенства:
Теорема.
M ( )
P A
,
A
M ( )
P A 1
.
A
□
:
х1 < х2 < … < хk ≤ A < хk+1 < … < хn
x1 х2
…
xk
А xk+1 … xn
x
185.
Неравенство Маркова (лемма Чебы шева)Запишем выражение для математического ожидания
x1 p1 x2 p2 ... xk pk xk 1 pk 1 ... xn pn M ( ),
где
pi P( xi ),
i 1, 2, ..., n.
xkk 1 pkk 1 ... xn pn M( ).
А pk 1 ... pn M ( ),
или
MM(( ))
pp ..... pp
..
k 1 nn
А
P( A)
■
186.
Неравенство Чебы шеваТеорема. Для любой случайной величины, имеющей
математическое
ожидание
и
дисперсию,
справедливо
неравенство
P a 1
где а=М( ), ε >0.
D
2
,
M ( )
P A 1
.
A
□
1=( –а)2,
P a
2
2
1
M a
2
2
.
a2 равносильно неравенству
M a D( ),т.е. представляет дисперсию ,
Так как неравенство
a ,а
A= ε2
2
2
то получим доказываемое неравенство.
■
187.
Частны е случаи неравенства Чебы шеваа)
случайная
распределения
величина,
имеет
биномиальный
закон
a M np, D npq
npq
P m np ε 1 2 .
ε
m,
б) случайная величина – частость события в n независимых
испытаниях, в каждом из которых оно может произойти с
pq
m
вероятностью р,
n , M p, D
n
m
pq
P p ε 1 2 .
nε
т
Замечание. Если M( )>A, или D( )>ε2, то неравенства Маркова
и Чебышева могут привести к тривиальным результатам типа P >–a
(a >0) или P< b (b >1), которые очевидны и без использования
данных неравенств.
188.
Теорема Чебы шеваТеорема. Если дисперсии n независимых случайных величин 1, 2,
…, n ограничены одной и той же постоянной, то при n→∞ средняя
арифметическая случайных величин сходится по вероятности к
средней арифметической их математических ожиданий a1, a2, …, an,
т.е.
1 .... n a1 .... an
lim P
1,
n
n
n
или
n
i
i 1
n
a
a
i
Р
i 1
.
n
n
189.
Теорема Чебы шева□ Применим неравенство Чебышева к случайной величине
1 ... n
.
n
Найдем
1 ... n 1
a1 ...an
M M
M
...
M
,
1
n
n
n
n
... n
D D 1
n
1
D ... D n
2 1
n
nC C
11
C
...
C 2 .
2 C
...
C
n
n
n n раз
(учли, что все дисперсии D( i)≤ C (C– постоянная), и случайные
величины i – независимые, что позволяет дисперсию суммы
случайных величин представить в виде суммы дисперсий).
190.
Теорема Чебы шеваТеперь неравенство Чебышева для случайной величины
1 ... n
примет вид:
n
.... n a1 .... an
D
P 1
1
.
n
n
n
C то
n ,
D
С/n
C
1
1
1
2
2
n 2
Так как по доказанному D
и от неравенства перейдем к более сильному неравенству
1 .... n a1 .... an
С
P
1 2 .
n
n
n
191.
Теорема Чебы шеваС
0,
В пределе при
n
2
n
и получаем доказываемую формулу
1 .... n a1 .... an
lim P
1,
n
n
n
■
Замечание. Неравенство Чебышева для средней арифметической
случайных величин
.... n a1 .... an
С
P 1
1 2 .
n
n
n
имеет самостоятельное значение и может быть использовано для
решения задач.
192.
Теорема Чебы шеваСмысл теоремы Чебышева состоит в том, что при большом числе
случайных величин их средняя – величина случайнnая как угодно
мало (≤ ε) отличается от неслучайной величины
,
ai / n
т.е.
i 1
практически перестает быть случайной с вероятностью, как угодно
близкой к 1.
Выясним смысл формулировки «сходимостьn по вероятaности»,
записываемой в виде.
a
Понятие предела переменной величины
i 1
n
i
i
Р
i 1 .
n
n
lim a , или a при n
n
или ее сходимость, означает, что начиная с некоторого момента ее
изменения, для любого (даже сколько угодно малого) ε >0 будет
верно неравенство |x–a|<ε.
193.
Теорема Чебы шеваСходимость по вероятности
a ,
Р
n
означает, что неравенство |x–a|<ε, начиная с некоторого момента
изменения переменной , будет выполняться не в любом случае, но
почти всегда, в подавляющем числе случаев, т.е. с вероятностью,
сколь угодно близкой к 1 при n .
194.
Теорема Чебы шеваТеорема Чебышева имеет большое практическое значение.
Например, деятельность страховых компаний, расчеты страховых
взносов и премий основаны на том, что известные средние убытки
застрахованных лиц за прошедший период в силу закона больших
чисел практически не изменятся за период страхования.
В финансовом анализе дисперсия случайной величины –
доходности некоторого актива (акции, ценной бумаги) характеризует
его риск. Действие закона больших чисел проявляется в уменьшении
дисперсии средней случайных величин с ростом n.
Поэтому, например, увеличение числа ценных бумаг разного вида
приводит к снижению риска составленного из этих бумаг
инвестиционного портфеля. Отсюда следует один из принципов
работы
на
финансовом
рынке,
известный
как
принцип
диверсификации (разнообразия) и вполне согласующийся с
народной мудростью: «не клади все яйца в одну корзину».
195.
Теорема БернуллиТеорема. Частость события в n повторных независимых
испытаниях, в каждом из которых оно может произойти с одной и
той же вероятностью р, при n
сходится по вероятности к
вероятности р этого события в отдельном испытании:
или
□
m
lim p 1,
n
n
m
Р
p.
n
n
Заключение
теоремы
непосредственно
неравенства Чебышева для частости событий при
m
pq
P p ε 1 2 .
nε
т
вытекает
n .
■
из
196.
Теорема БернуллиСмысл теоремы Бернулли состоит в том, что частость m/n –
величина случайная при большом n как угодно мало отличается от
вероятности p – величины неслучайной, т.е. практически перестает
быть случайной с вероятностью, как угодно близкой к 1 при n .
Теорема
Бернулли,
являющаяся
следствием
теоремы
Чебышева, дает теоретическое обоснование замены неизвестной
вероятности
события
его
частостью,
или
статистической
вероятностью. Например, неизвестную вероятность рождения
мальчика в соответствии с этой теоремой можно заменить его
частостью, которая по многолетним данным составляет приближенно
0,515.
197.
Центральная предельная теорема – теоремаЛяпунова
Теорема. Если случайная величина представляет
собой сумму очень большого числа взаимно независимых
случайных величин i, i=1,2,3,...,n, имеющих конечные
математические ожидания и дисперсии, влияние каждой из
которых на всю сумму ничтожно мало, т.е. ни одна из
величин по своему значению резко не отличается от
остальных. то при неограниченном увеличении n
распределение
нормальному с
приближается к
ожиданием,
математическим
равным
сумме
математических ожиданий и дисперсией, равной сумме
дисперсий..
N M , D
198.
Центральная предельная теорема – теоремаЛяпунова
Согласно теореме Ляпунова, при решении многих
практических задач, связанных со случайной величиной ,
являющейся
средним
арифметическим
наблюдаемых
значений случайной величины , можно утверждать, что
среднеарифметическое значение сл.в. распределено по
нормальному закону:
N a, 2 / n
199.
Спасибо за внимание200.
Анализ данныхЛекция
Генеральная совокупность и выборка.
Вариационные ряды и их графическое
представление
201.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
Лекция 6
202.
Генеральная совокупность ивыборка
Анализ данных – дисциплина, опирающаяся на
методы и модели, изучаемые в математической
статистике.
Математическая статистика – раздел математики,
тесно связанный с теорией вероятностей.
Статистика изучает методы сбора и анализа
результатов наблюдений массовых случайных явлений с
целью выявления существующих закономерностей.
203.
Генеральная совокупность ивыборка
Различие
между
теорией
вероятности
и
математической статистикой заключается в том, что
типичная задача теории вероятности – по известным
вероятностям простых случайных событий вычислить
вероятность более сложного события.
Типичная задача математической статистики – на
основании результатов наблюдений оценить вероятность
случайного события или характеристики случайной
величины.
Для
осуществления
последнего
широко
используются выборочные методы.
204.
Генеральная совокупность ивыборка
Выборочные методы анализа данных являются
одной из составных частей математической статистики,
предметом которой является изучение совокупности
однородных
объектов
относительно
некоторого
качественного
или
количественного
признака,
характеризующего
эти
объекты
по
результатам
наблюдений.
совокупностью
Определение.
Генеральной
называют совокупность всех мысленно возможных
объектов данного вида,
над которыми проводятся
наблюдения.
205.
Генеральная совокупность ивыборка
В практике статистических обследований различают
два вида наблюдений:
сплошное, когда изучаются все объекты генеральной
совокупности относительно некоторого признака;
не сплошное (или выборочное), когда изучается только
часть объектов (выборочный метод) генеральной
совокупности.
Определение. Выборочной совокупностью, или
просто выборкой, называют совокупность случайно
отобранных объектов из генеральной совокупности.
206.
Генеральная совокупность ивыборка
Объемом
совокупности
(выборочной
генеральной)
называют
число
объектов
совокупности:
N – объем генеральной совокупности;
n – объем выборочной совокупности.
Предполагается, что N>n.
или
этой
Генеральная совокупность может
конечной, так и бесконечной ( N ).
как
быть
207.
Генеральная совокупность ивыборка
Суть выборочного метода состоит в том, чтобы
по некоторой части генеральной совокупности
(выборке) выносить суждения о ее свойствах в целом.
Для того, чтобы по выборке можно было
достаточно уверенно судить об изучаемой случайной
величине, выборка должна быть репрезентативной
(или представительной).
Репрезентативность
выборки
означает,
что
объекты выборки достаточно хорошо представляют
генеральную совокупность.
208.
Генеральная совокупность ивыборка
Репрезентативность
выборки
обеспечивается
выполнением трех требований:
1. Случайность отбора объектов выборки из
генеральной
совокупности,
т.е.
любой
объект
генеральной совокупности может быть отобран для
исследования.
При этом все объекты генеральной совокупности
имеют одинаковую вероятность попасть в выборку.
2. Независимость исследования каждого отдельного
объекта выборки от результатов,
полученных для
других объектов.
3. Достаточный объем выборки.
209.
Генеральная совокупность ивыборка
Возможны
два способа образования выборки:
повторный и бесповторный отбор.
Определение. Повторной называют выборку, при
которой
отобранный
объект
(перед
отбором
следующего)
возвращается
в
генеральную
совокупность.
Определение. Бесповторной называют выборку,
при которой отобранный объект в генеральную
совокупность не возвращается.
210.
Статистические и вариационныеряды
Любой
исследуемый
признак
объектов
генеральной совокупности, независимо от наших
знаний о нем, имеет некоторое статистическое
распределение
и
может
рассматриваться
как
случайная величина .
Тогда,
значение исследуемого признака у
конкретного объекта выборки – это реализация
случайной величины
, а результаты наблюдений,
полученные для всех объектов выборки представляют
собой
множество расположенных
в беспорядке
реализаций случайной величины :
X 1 , X 2 ,..., X n
211.
Вариационные рядыОпределение. Ранжирование – это упорядочение
полученных данных в порядке возрастания (или
убывания).
проведения
операции
ранжирования
После
получим:
X 1 X 2 ... X n ,
где элемент
– называется k –ой
X k
порядковой статистикой.
212.
Вариационные рядыЕсли изучаемая случайная величина является
дискретной,
то
после
проведения
операции
ранжирования опытные данные как правило нетрудно
объединить в группы так, что в каждой отдельной
группе возможные значения случайной величины будут
одинаковыми.
Определение. Различные возможные значения
случайной величины , соответствующие отдельной
группе сгруппированного ряда наблюдаемых данных,
называются вариантами и обозначаются
x1, x2 ,..., xm
При этом
x1 x2 ... xm .
213.
Вариационные рядыДля
каждой
группы
сгруппированного
ряда
определяется ее численность, т.е. число, которое
показывает, сколько раз встречается соответствующий
вариант в ряде наблюдений.
Определение. Численность отдельной группы
сгруппированного
ряда
наблюдаемых
данных
называется частотой или весом соответствующего ей
варианта и обозначается ni (i=1,2,…,m), где i – номер
варианта.
214.
Вариационные рядыОпределение.
Отношение
частоты
данного
варианта к объему выборки называется частостью или
долей этого варианта и обозначается wi , т.е.:
Очевидно, что:
ni
wi
m n
n ni
i 1
215.
Вариационные рядыОпределение.
Сгруппированным
дискретным
вариационным рядом называется ранжированный в
порядке возрастания (или убывания) ряд вариантов с
соответствующими им частотами или частостями,
который представляют в виде таблицы:
варианты, xi
частоты, ni
частости, wi
x1
n1
w1
x2
n2
w2
…
…
…
xm
nm
wm
n
1
216.
Вариационные рядыПример 1. Изучается успеваемость студентов
некоторого вуза по математике. По схеме собственнослучайной бесповторной выборки из 500 студентов
вуза было отобрано 50. Результаты опроса студентов
представляют собой следующий набор чисел:
3;4;5;4;2;3;3;3;5;4;3;5;5; 2;3;5;3;5;3;5;4; 4;3;3;4;
3;3;3;4;3;4;3;5;3;4;4;3;5;3;3;5;
4;2;5;3;4; 2;3;5;4.
n 50
Построить дискретный вариационный ряд.
217.
Вариационные ряды3;4;5;4;2;3;3;3;5;4;3;5;5; 2;3;5;3;5;3;5;4; 4;3;3;4;
3;3;3;4;3;4;3;5;3;4;4;3;5;3;3;5;
4;2;5;3;4; 2;3;5;4.
n 50
варианты, xi
частоты, ni
n
частость, w i
i
n
2
4
3
21
4
13
5
12
50
0,08
0,42
0,26
0,24
1
218.
Вариационные рядыНакопленная частота определяется как сумма
частот вариант, не превышающих данного варианта,
т.е.
i
nx n1 n2 ... ni n j
i
j 1
Поделив
накопленную
выборочной совокупности,
частость
частоту
получим
на
объем
накопленную
i
n
n
...
n
1
i
1 2
nj
wx
n
n
n j 1
nx
i
i
219.
Вариационные ряды220.
Вариационные рядыЕсли изучаемая случайная величина является
непрерывной,
то
ранжирование
и
группировка
наблюдаемых значений, как правило, не позволяет
выделить характерные черты их варьирования.
В подобных случаях
вариационный ряд.
строится
интервальный
Для этого также проводят группировку, разбивая
весь интервал варьирования от xmin до xmax на отдельные
интервалы, так чтобы каждое возможное значение
принадлежало только одному из интервалов разбиения.
221.
Вариационные рядыЧисло возможных значений изучаемой случайной
величины, принадлежащих i-му интервалу будем также
обозначать ni (частота попадания в i-ый интервал).
Число интервалов m следует брать не очень
большим, чтобы после группировки ряд не был
громоздким, и не очень малым, чтобыне потерять
особенности распределения признака.
Рекомендуемое число интервалов
согласно формуле Стерджеса:
m 1 3,322 lg n .
выбирается
222.
Вариационные рядыДлины интервалов можно брать как равными, так и
различными.
Будем предполагать, что длины интервалов
одинаковые, величина которых (ширина интервала)
определяется соотношением:
xmax xmin
h
m
223.
Вариационные рядыГраницы интервалов рассчитываются по правилу:
a0 xmin , a1 a0 h, a2 a1 h, ...
Формирование интервалов заканчивается, как
только для правой границы
очередного интервала
выполняется условие:
am xmax
224.
Вариационные рядыСгруппированным интервальным
упорядоченная
вариационным
рядом
называется
совокупность
интервалов
варьирования
значений
случайной величины с соответствующими частотами или
частостями попаданий в каждый из них значений
величины.
Определение.
Очень часто интервальный ряд для простоты
исследований условно заменяют дискретным. В этом
случае в качестве вариант хi такого
ряда берутся
серединные значения интервалов разбиения, т.е.
ai 1 ai
xi
,
2
i 1,m
а соответствующую интервальную частоту ni – за частоту
этого варианта.
25
225.
Вариационные рядыПример 2. Для исследования доходов работников
предприятия, численность которого составляет 1600
человек, по схеме собственно-случайной бесповторной
выборки было отобрано 160 человек. Получены
следующие данные о месячном доходе (у.е.):
14; 25; 27; ; 32; 10.
160 значений
Находим минимальное хmin= 5, и максимальное
значения xmax= 45.
Разобьем полученные данные по отдельным
интервалам, т.е. проведем группировку.
26
226.
Вариационные рядыОпределяем число интервалов разбиения и их
длину:
m 1 3,322 lg160 8
h
45 5
5.
8
Интервалы
5-10
10-15 15-20 20-25 25-30 30-35 35-40 40-45 итого
частоты
7
15
26
40
32
21
14
5
160
227.
Вариационные рядыТаким образом, в нашем примере с заработной
платой, получается следующий ряд:
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35
35-40
40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
итог
о
160
228.
Вариационные рядыДля каждого интервала
частоты и частости.
определяем накопленные
интервалы
5-10
10-15 15-20 20-25 25-30 30-35 35-40 40-45
варианты, хi
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты, ni
7
15
26
40
32
21
14
5
накопленная
частота, nx i
7
22
48
88
120
141
155
160
накопленная
частость,
0,044
0,138 0,300 0,550 0,750 0,881 0,969
1,0
wx
i
160
229.
Графическое представлениедискретных вариационных рядов
Графической
иллюстрацией
дискретных
вариационных рядов является полигон
частот или
относительных частот.
Полигон частот (или относительных частот) –
ломаная на плоскости, состоящая из отрезков прямых,
соединяющих точки с координатами (хi, ni) или (хi, wi), i
= 1, 2, …, m.
230.
Графическое представлениедискретных вариационных рядов
Для рассмотренного в примере 1 ряда полигон
частот будет следующим:
варианты, xi
частоты, ni
n
частость, w i
i
n
2
4
3
21
4
13
5
12
50
0,08
0,42
0,26
0,24
1
5
х
ni
wi
25
0,5
20
0,4
15
0,3
10
0,2
5
0,1
0
2
3
4
231.
Графическое представлениедискретных вариационных рядов
Эмпирической
называется функция
функцией
распределения
F (x) ,
*
nx
n
где
nx - число вариант, строго меньших х, а n –
объем выборки.
232.
Графическое представлениедискретных вариационных рядов
Для сгруппированного дискретного вариационного
ряда
для
распределения
любого
х
эмпирическая
представляет
собой
функция
накопленную
частость предшествующей варианты, т.е.
0, x x1,
nx
*
,
F (x) wx
n
1, x xn .
i 1
i 1
xi 1 x xi , i 2,3,...,n
233.
Графическое представлениедискретных вариационных рядов
Эмпирическая функция распределения для ряда
варианты, xi
частоты, ni
n
частость, w i
i
n
накопленная
частота, nx
2
4
3
21
4
13
5
12
50
0,08
4
0,42
25
0,26
38
0,24
50
1
0,08
0,5
0,76
1
i
накопленная
частость, wx
i
0, если x 2,
0, 08 если 2 x 3,
*
F (x) 0,5 если 3 x 4
0, 76 если 4 x 5,
1, если x 5.
234.
Графическое представлениедискретных вариационных рядов
Кумулятивной
кривой
называется
кривая
накопленных частот (или накопленных частостей).
Для
дискретного
вариационного
ряда
кумулятивная кривая представляет собой ломаную
линию, состоящую из отрезков прямых, соединяющих
точки (xi , nxi ) или
(xi , wxi ) ,
где nx – число вариант не превышающих
xi ,
i
а
x – накопленная частость .
w
i
235.
Графическое представлениедискретных вариационных рядов
Пример 4. Построить график
функции распределения. На том
изобразить кумулятивную кривую.
эмпирической
же графике
50 1,0
40 0,8
30 0,6
20 0,4
10 0,2
0
2
3
4
5
х
236.
Графическое представлениенепрерывных вариационных рядов
Для графического изображения интервальных
вариационных рядов также
служит гистограмма,
представляющая
собой
ступенчатую
фигуру,
составленную из прямоугольников с основаниями,
равными интерваламзначений
признака длины k и
высотами, равными частотам ni или частостям wi
вариантов данных интервалов.
Если соединить середины верхних оснований
прямоугольников отрезками прямых, то можно получить
полигон того же распределения.
237.
Графическое представлениенепрерывных вариационных рядов
Площадь гистограммы будет численно равна
произведению длины интервала k на объем выборки n,
т.е.
S h n,
а если в качестве высот брать
частости, то
площадь будет равна длине интервала разбиения, т.е.
S h
238.
Графическое представлениенепрерывных вариационных рядов
Если же при построении гистограммы в качестве
высот прямоугольников взять отношение частости к
длине интервалов разбиения, то получим график
эмпирической функции плотности распределения f * (x)
Очевидно, что площадь под
функции будет равна единице.
графиком такой
239.
Графическое представлениенепрерывных вариационных рядов
Построим гистограмму (эмпирическую функцию
плотности
распределения),
полигон
частот
и
кумулятивную
кривую
(эмпирическую
функцию
распределения) для ряда в примере 2.
интервалы
5-10
10-15 15-20 20-25 25-30 30-35 35-40 40-45
варианты, хi
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты, ni
7
15
26
40
32
21
14
5
накопленная
частота, nx i
7
22
48
88
120
141
155
160
накопленная
частость,
0,044
0,138 0,300 0,550 0,750 0,881 0,969
1,0
wx
i
160
240.
Графическое представлениенепрерывных вариационных рядов
ni
50
40
30
20
10
0
10
20
30
40
50
х
241.
Графическое представлениенепрерывных вариационных рядов
При
построении
эмпирической
функции
распределения для интервального вариационного ряда
будем учитывать, что мы имеем лишь значения этой
функции только на концах интервалов (накопленные
частости – последняя строка таблицы ).
Поэтому для ее графического изображения
целесообразно доопределить функцию, соединив
точки графика, соответствующие концам интервалов,
отрезками прямой.
Такое
определение
эмпирической
функции
распределения приводит к тому, что полученная
ломаная будет совпадать с кумулятивной кривой.
242.
Графическое представлениенепрерывных вариационных рядов
nx
wx
160
1,0
128 0,8
96
0,6
64
0,4
32
0,2
0
10
20
30
40
50
х
243.
Спасибо за внимание244.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
Лекция 7
245.
Анализ данныхЛекция
Статистические характеристики
вариационных рядов
2.Точечные и интервальные оценки
параметров генеральной совокупности
1.
246.
Статистические характеристикивариационных рядов
Определение. Средней арифметической не
сгруппированного вариационного ряда называется
средняя арифметическая его вариант:
1 n
x xi
n i 1
247.
Статистические характеристикивариационных рядов
Определение. Средней
арифметической
сгруппированного вариационного ряда называется
сумма
произведений
всех
вариант
ряда
на
соответствующие им частоты, деленная на сумму
частот (объем):
1 m
x
xn
n
i i
i 1
где xi –варианты дискретного ряда или середины
интервалов интервального ряда; ni – соответствующие
им частоты.
248.
Статистические характеристикивариационных рядов
Определение. Дисперсией не сгруппированного
вариационного
ряда
называется
средняя
арифметическая квадратов отклонений вариант от их
средней арифметической:
n
2
1
s xi x
n i 1
2
249.
Статистические характеристикивариационных рядов
Пример. Дана выборка
5, 2,1, 5, 4, 5, 3, 2, 3, 6.
Построить вариационный ряд.
Вычислить
среднюю
арифметическую
и
дисперсию.
Решение. Запишем данный ряд в порядке
неубывания его вариант:
1, 2, 2, 3, 3, 4, 5, 5, 5, 6.
Средняя арифметическая:
1
x (1 2 2 3 3 4 5 5 5 6) 3,6.
10
Дисперсия:
1
((1 3,6)2 (2 3,6)2 (2 3,6)2 (3 3,6)2
10
(3 3,6)2 (4 3,6)2 (5 3,6)2 (5 3,6)2
s2
(5 3,6)2 (6 3,6)2 ) 2,44.
250.
Статистические характеристикивариационных рядов
Определение.
Дисперсией
сгруппированного
вариационного
ряда
называется
средняя
арифметическая квадратов отклонений вариантов от их
средней
арифметической.
Соответственно,
генеральная и выборочная дисперсии определяются
2
по формулам: 2 1 m
s xi x ni
n i 1
Теорема.
Дисперсия
вариационного
ряда
определяется по формуле:
m
s2
1
xi 2ni x 2 x2 x 2
n i 1
251.
Статистические характеристикивариационных рядов
Пример. Вычислим среднюю арифметическую и
дисперсию для вариационного ряда, представленного в
примере:
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35
35-40 40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
x
1
(7,5 7 12,5 15 17,5 26 22,5 40 27,5 32
160
32,5 21 37,5 14 42,5 5) 24,34
итог
о
160
252.
Статистические характеристикивариационных рядов
Вычислим среднюю арифметическую и дисперсию
для вариационного ряда, представленного в примере:
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35
35-40 40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
x2
1
(7,52 7 12,52 15 17,52 26 22,52 40 27,52 32
160
32,52 21 37,52 14 42,52 5) 662,63
s2 x2 x 2 662,63 24,342 70,19
итог
о
160
253.
Статистические характеристикивариационных рядов
Медианой
вариационного ряда называется
значение признака, приходящееся на середину
ранжированного ряда наблюдений.
Для рядов с нечетным числом членов медиана
будет равна срединному варианту
M e X n 1
2
а для ряда с четным числом членов – полусумме
двух срединных вариант, т.е.
Xn Xn
1
2 .
M e 2
2
254.
Статистические характеристикивариационных рядов
Пример. Вычислим медиану для ряда
1, 2, 2, 3, 3, 4, 5, 5, 5, 6.
Решение.
Ряд с четным
Следовательно, медиана равна
срединных вариант, т.е.
3 4
Me
3,5.
2
числом вариант.
полусумме двух
255.
Статистические характеристикивариационных рядов
Пример. Вычислить
медиану для дискретного
вариационного ряда представленного в примере 1.
варианты, xi
частоты, ni
n
частость, w i
i
n
2
4
3
21
4
13
5
12
50
0,08
0,42
0,26
0,24
1
X 25 3
X 26 4
3 4
M e
3,5.
2
256.
Статистические характеристикивариационных рядов
Для интервального вариационного ряда находится
медианный интервал, на который приходится середина
ряда, т.е. первый интервал, где сумма накопленных
частот превышает половину наблюдений от общего
объема выборки.
что
функция
плотности
Предполагая,
распределения признака на медианном интервале
является постоянной,
значение медианы на этом
интервале
находят
с
помощью
линейного
интерполирования по формуле:
n
n x,e 1
M e x e 2
h
ne
257.
Статистические характеристикивариационных рядов
Пример. Вычислить медиану для интервального
вариационного ряда, полученного в примере 2.
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35
35-40 40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
xe 20, ne 40, h 5, nx,e 1 48
n 160.
160
48
M e 20 2
5 24 .
40
итог
о
160
258.
Статистические характеристикивариационных рядов
Модой вариационного ряда называется варианта,
которой соответствует наибольшая частота.
Если интервальный ряд имеет одинаковую ширину
интервалов, то за приближенное значение моды берут
середину модального интервала, т.е. интервала с
наибольшей частотой.
Точное значение моды можно получить по
формуле:
M o xм h
nм nм 1
,
(nм nм 1 ) (nм nм+1 )
259.
Статистические характеристикивариационных рядов
Пример. Вычислить моду для ряда
1, 2, 2, 3, 3, 4, 5, 5, 5, 6.
Решение.
M o 5.
260.
Статистические характеристики,
вариационных
рядов
,
Пример. Вычислить моду вариационных рядов,
рассмотренных выше в примерах 1 и 2.
В примере 1
варианты, xi
частоты, ni
n
частость, w i
i
n
2
4
3
21
4
13
5
12
50
0,08
0,42
0,26
0,24
1
M o 3.
т.к. эта варианта имеет наибольшую частоту,
равную 21.
261.
Статистические характеристикивариационны, х рядов
Во втором примере воспользуемся приведенной
выше формулой. Из вида вариационного ряда следует,
что:
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35 35-40
40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
xм 20
h 5
nм 40
nм-1 26
M o 20 5
40 26
23,18.
(40 26) (40 32)
nм+1 32
итог
о
160
262.
Статистические характеристикивариационных рядов
Определение. Генеральной долей р признака А
называется отношение числа М членов генеральной
совокупности с признаком А к ее объему N, т.е.
p=M/N.
Определение. Выборочной долей признака А
называется отношение числа m членов выборочной
совокупности с признаком А к ее объему n, т.е.
=m/n.
263.
Статистические характеристикивариационных рядов
Пример. Вычислить выборочную долю студентов
сдавших экзамен на хорошо и отлично.
варианты, xi
частоты, ni
n
частость, w i
i
n
2
4
3
21
4
13
5
12
50
0,08
0,42
0,26
0,24
1
13 12 0,5.
50
264.
Статистические характеристикивариационных рядов
Пример. Вычислить выборочную долю работников
предприятия, имеющих заработную плату не большую
20 у.е.
Интервалы
5-10
10-15
15-20
20-25
25-30
30-35 35-40
40-45
сред.
знач.
7,5
12,5
17,5
22,5
27,5
32,5
37,5
42,5
частоты
7
15
26
40
32
21
14
5
7 15 26 48 0,3.
160
160
итог
о
160
265.
Точечные оценки параметровгенеральной совокупности
Исчерпывающей вероятностной характеристикой
случайной величины является ее закон распределения
– функция распределения или функция плотности
распределения.
Для описания законов распределения достаточно
знать его числовые характеристики или параметры
распределения.
В
качестве
параметров
могут
выступать
математическое
ожидание,
дисперсия,
среднее
квадратическое отклонение, доля и др.
266.
Точечные оценки параметровгенеральной совокупности
По выборке можно находить лишь приближенные
значения указанных числовых характеристик, т.е. их
оценки.
В отличие от оцениваемого параметра – величины
неслучайной – выборочная оценка является величиной
случайной. Ее значение существенно зависит от
объема выборки и ее состава. Будем ее обозначать .
Выборочная
Определение.
числовая
характеристика
качестве
,
используемая
в
приближенного
значения
неизвестной
числовой
характеристики
генеральной
совокупности
t,
называется ее точечной статистической оценкой.
267.
Точечные оценки параметровгенеральной совокупности
Как правило, существует некоторое множество
оценок одной и той же числовой характеристики
генеральной совокупности.
Так, если оценивается математическое ожидание
некоторого признака генеральной совокупности –
генеральная средняя , то в качестве его оценки по
выборке можно, например, принять выборочную
среднюю, моду медиану полусумму наименьшего и
наибольшего значений по выборке и т.д.
Неоднозначность выбора оценки приводит к тому,
что необходимо решить какая оценка обеспечивает
наибольшую точность определения соответствующих
числовых характеристик генеральной совокупности.
268.
Точечные оценки параметровгенеральной совокупности
Всякая оценка постоянной величины с помощью
случайной
величины
должна
обладать
тремя
следующими свойствами:
а) свойство несмещенности;
б) свойство состоятельности;
в) свойство эффективности.
269.
Точечные оценки параметровгенеральной совокупности
Состоятельность.
Оценка
n генеральной
характеристики t называется состоятельной, если она
удовлетворяет закону больших чисел, т.е. сходится по
вероятности к оцениваемому параметру:
n t.
p
т.е.
lim P n t 1
n
Указанная в определении последовательность
числовых оценок n можно получить, например,
увеличивая объем выборки.
270.
Точечные оценки параметровгенеральной совокупности
Смысл свойства состоятельности состоит в том,
что при увеличении объема выборки растет
уверенность (вероятность) в том, что отклонение
оценки от оцениваемой числовой характеристики
генеральной совокупности по абсолютной величине
становиться сколь угодно малым.
Если оценка не является состоятельной, то она не
имеет практического смысла, так как в этом случае
увеличение объема исходной информации не будет
приближать эту оценку к истинной.
271.
Точечные оценки параметровгенеральной совокупности
Несмещенность.
Оценка
n
генеральной
характеристики t называется несмещенной, если для
любого
фиксированного
числа
наблюдений
n
выполняется равенство
M n t,
т.е. математическое ожидание оценки равно
оцениваемой неизвестной характеристике.
Смысл несмещенности состоит в том, что если
точечная оценка обладает этим свойством, то она
будет группироваться около действительного значения
данного параметра и при массовом применении такой
оценки, она в среднем будет равна этому значению.
272.
Точечные оценки параметровгенеральной совокупности
Эффективность.
Оценка
n
генеральной
характеристики t называется эффективной, если она
среди всех прочих несмещенных оценок той же самой
характеристики обладает наименьшей дисперсией.
Для
того
чтобы
выяснить,
является
ли
несмещенная и состоятельная оценка эффективной,
необходимо сравнить дисперсию этой оценки с
минимальной дисперсией. В некоторых случаях этот
минимум хорошо известен.
273.
Выборочная доля как точечная оценкагенеральной доли
Теорема.
Выборочная
доля
=m/n
есть
несмещенная, состоятельная и эффективная оценка
генеральной доли p=M/N, причем ее дисперсия
pq
2
,
для повторнойвыборки
n
2
pq
n
1
,
n N
для бесповторной выборки
274.
Выборочная средняя как точечнаяоценка генеральной средней
Теорема. Выборочная средняя
есть
х
несмещенная, состоятельная и эффективная оценка
генеральной средней х0 , причем ее дисперсия
2
2
x
2
,
n
x2 1 n ,
n N
для повторнойвыборки
для бесповторной выборки
275.
Выборочная дисперсия как точечнаяоценка генеральной дисперсии
Теорема. Выборочная дисперсия s2 повторной и
бесповторной
выборок
есть
смещенная
и
состоятельная оценка
дисперсии генеральной
совокупности .
n 1 2
2
Ms
n
Несмещенной
и
оценкой
состоятельной
генеральной дисперсии является
исправленная
выборочная
дисперсия,
которая
определяется
соотношением:
n 2
s€2
n 1
s
276.
Интервальные оценки параметровгенеральной совокупности
Интервальной оценкой параметра t называется
числовой интервал 1 , 2 , который с
заданной
вероятностью накрывает неизвестное значение
параметра t.
1
t
2
Такой интервал называется доверительным, а
вероятность – доверительной вероятностью
или надежностью оценки.
277.
Доверительная вероятность ипредельная ошибка выборки
Очень часто доверительный интервал выбирается
симметричным относительно параметра t , т.е.
t ,t
Наибольшее отклонение выборочной средней
(или доли) от генеральной средней (или доли),
которое возможно с заданной доверительной
вероятностью , называется предельной ошибкой
выборки.
278.
Доверительная вероятность ипредельная ошибка выборки.
Ошибка
является
ошибкой
репрезентативности
(представительности)
выборки. Она возникает только вследствие того, что
исследуется не вся совокупность, а лишь ее часть
(выборка), отобранная случайно.
279.
Спасибо за внимание280.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
Лекция 8
281.
Анализ данныхЛекция
Интервальные оценки параметров
генеральной совокупности
282.
Построение доверительного интервалапо большим выборкам
Теорема. Вероятность того, что отклонение
выборочной средней (или доли) от генеральной
средней (или доли) не превзойдет число > 0 (по
абсолютной величине), равна:
P x x0 2Ф(u) , где u
,
P p 2Ф(u) , где u
Ф(u)
–
соотношением:
функция
Ф( х )
1
Лапласа,
x t 2
2 dt
e
2 0
x
.
определяемая
283.
Построение доверительного интервалапо большим выборкам
Определение.
Среднее
квадратическое
х
отклонение
выборочной средней
и
выборочной доли собственно случайной выборки
называются
средними
квадратическими
(стандартными)
ошибками
выборки
соответсвенно при оценке генеральной средней и
доли.
284.
Построение доверительного интервалапо большим выборкам
Следствие 1. При заданной доверительной
вероятности предельная ошибка выборки равна
u-кратной величине средней квадратической ошибки,
где 2Ф(u) = , т.е.
u x
,
u
.
Интервальные
оценки
Следствие
2.
(доверительные интервалы) для генеральной средней
и генеральной доли могут быть найдены по
формулам:
x x0 x
, p
.
285.
Построение доверительного интервалапо большим выборкам
ОцениФормулы средних квадратических ошибок
ваемы
выборки
й
Повторная выборка
Бесповторная выборка
параметр
2
2
n
s
2
2
x n 1 N n 1 Nn
s
x
Средняя
n
Доля
n
pq
(1 )
1 n (1 ) 1 n
pq
n
N
n
N
n
n
286.
,Построение доверительного
интервала по большим выборкам
Пример. Найти границы, в которых с вероятностью
0,9876 заключена средняя месячная заработанная плата
всех работников данного предприятия.
Решение. По условию имеем:
2
s
70,19
x
24,34
N 1600
n 160
Вычислим
среднюю
квадратическую
ошибку
бесповторной выборки:
s2
n
70,19
160
1
0,63
x
1
160 1600
n N
По таблице значений функции Лапласа для
доверительной вероятности 0,9876 находим u 2,5.
Следовательно: 2,5 0,63 1,575.
24,34 1,575 x0 24,34 1,575
Доверительный
или
интервал:
22,765 x0 25,915
287.
Построение доверительногоинтервала по большим выборкам
Пример. Найти вероятность того, что средняя
месячная заработанная плата
всех работников
предприятия отличается от среднего дохода, полученного
по выборки не более, чем на 1 у.е. по абсолютной
величине.
Решение. По условию имеем:
1
Находим искомую доверительную вероятность по
формуле:
P x x0 2 Ф
x
или
1
2 Ф 1,59 2 0,4441 0,8882
2 Ф
0,63
288.
,Построение доверительного
интервала по большим выборкам
Пример. Найти границы, в которых с вероятностью
0,9545 заключена доля работников предприятия, средняя
месячная заработанная плата которых не более 20 у.е.
Решение. По условию имеем:
n 160
0,3
N 1600
Вычислим
среднюю
квадратическую
ошибку
бесповторной выборки для доли:
w
w(1 w) n
0,3 (1 0,3)
160
1
1
0,034
n
160
N
1600
По таблице значений функции Лапласа для
доверительной вероятности 0,9545 находим u 2.
Следовательно: u w 2 0,034 0,068
Доверительный
интервал:
0,3 0,068 p 0,3 0,068
или
0,233 p 0,368
289.
,Построение доверительного
интервала по большим выборкам
Пример. Найти вероятность того, что доля
работников предприятия, месячная заработанная плата
которых не превышает 20 у.е., отличается от полученной
по выборке доли не более, чем на 5% по абсолютной
величине.
Решение. По условию имеем: 0,05
Находим искомую доверительную вероятность по
формуле:
P w p 2 Ф
w
2 Ф 0,05 2 Ф 1,47 2 0,4292 0,8584.
0,034
290.
Объем выборкиДля проведения выборочного наблюдения весьма
важно правильно установить объем выборки n, который
в значительной степени определяет необходимые при
этом временные, трудовые и стоимостные затраты. Для
определения n необходимо задать надежность
(доверительную вероятность) оценки и
точность (предельную ошибку выборки ) .
Объем
выборки
находится
выражающей предельную ошибку
дисперсию признака.
из
формулы,
выборки через
291.
Объем выборкиОценива
е мый
параметр
Повторна
я
выборка
Бесповторная выборка
Средняя
u2 2
n 2
Nu2 2
n 2 2
u N 2
Доля
u 2 pq
n 2
n
Nu2 pq
u 2 pq N 2
292.
Объем выборкиЕсли найден объем повторной выборки n, то объем
соответствующей бесповторной выборки n' можно
nN
определить по формуле:
.
n
n N
Так как
N
1,
n N
то при одной и той же точности и надежности
оценок объем бесповторной выборки всегда будет
меньше объема повторной выборки: n n
Этим и объясняется тот факт, что на практике в
основном используется бесповторная выборка.
293.
Объем выборкиКак видно из представленных в таблице формул,
для определения объема выборки необходимо знать
характеристики генеральной совокупности, которые
неизвестны
и
для
определения
которых
предполагается провести выборочное исследование.
Поэтому, в качестве этих характеристик обычно
s2
используют
выборочные
данные
или
предшествующего
исследования
в
аналогичных
условиях.
294.
Объем выборкиЕсли никаких сведений о значениях 2 или р нет, то
организуют специальную пробную выборку небольшого
объема.
При оценки генеральной доли (если о ней ничего
не известно) вместо проведения пробной выборки
можно в формулах в качестве произведения pq взять
его максимально возможное значение, равное 0,25, но
при этом надо учитывать, что найденное значение
объема
выборки
будет
больше
минимально
необходимого для заданных точности и надежности
u2
оценок, т.е.
n
4 2
295.
Объе выборкиПример.
Определить
объем
бесповторной
выборки, чтобы с
вероятностью 0,9876 средняя
месячная заработанная плата, полученная по выборке
отличалась от генеральной средней не более чем на 1
у.е.
Решение. Сначала найдем объем повторной
выборки :
2
2
2
u s
2,5 70,19
n
439
2
2
1
Объем бесповторной выборки :
nN
439 1600
345
n
n N 439 1600
296.
Объем выборкиПример.
Определить
объем
бесповторной
выборки, чтобы с
вероятностью 0,9545 доля
работников
предприятия
средняя
месячная
заработанная плата которых не более 20 у.е.,
отличалась от полученной по выборке не более, чем на
5% (по абсолютной величине).
Найти то же число, если о выборочной доли ничего
неизвестно.
Решение. Сначала найдем объем повторной
u 2 w(1 w) 22 0,3 (1 0,3)
выборки :
n
336
0,05
nN
336 1600
n
278
Объем бесповторной выборки:
n N 336 1600
2
2
Если о выборочной доли ничего n u 2
400
2
2
4
4 0,05
неизвестно:
nN
400 1600
320
n
n N 400 1600
2
2
297.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности по
малой выборке при известной дисперсии
Пусть исследуемый признак в генеральной
совокупности описывается нормально распределенной
случайной величиной ξ: ~ N a, 2
Не нарушая общности можно считать, что все
элементы выборки
X1 , X 2 ,..., X n
независимы и одинаково распределены.
Пусть
M X i a,
D X i 2 .
298.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности по
малой выборке при известной дисперсии
Рассмотрим
выборочную
среднюю
арифметическую.
Найдем параметры закона распределения средней
арифметической:
1 n
1 n
1
M x M
M
X
n a a,
X
i
i
n
n i 1
n i 1
n
1 n
1
1
2
2
D x D X i
D
X
n
.
i
2
2
n
n i 1
n i 1
299.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при известной дисперсии
Для
построения
доверительного
интервала
рассмотрим случайную величину
x a
.
/ n
Эта случайная величина имеет стандартный
нормальный закон распределения:
1
1
x a 1
M M
M x a
M x a
a a 0,
/ n
/ n
/ n / n
2
n
1
x
a
n
D D
a 2 D x 0 2 1.
2D x
n
/ n
/ n
300.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при известной дисперсии
Если
дисперсия
генеральной
совокупности
известна, то задав доверительную вероятность γ,
найдем такое значение предельной ошибки выборки Δ,
при котором
P x a .
Зная, что случайная величина η имеет стандартное
нормальное распределение, перепишем последнее
соотношение в виде:
.
P x a P x a
2
/ n
n
/
n
/
301.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при известной дисперсии
Таким образом, необходимо найти такое значение
аргумента функции Лапласа
u
,
/ n
при котором 2 u .
Разрешая последнее соотношение относительно Δ,
получим:
u
.
n
Следовательно, доверительный интервал будет
иметь следующий вид:
u
u
x
a x
.
n
n
302.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при известной дисперсии
Нетрудно
заметить,
что
в
этом
случае
доверительный интервал совпадает с полученным
ранее доверительным интервалом для больших
выборок.
Однако использовать эту формулу можно лишь
тогда, когда генеральная дисперсия известна.
На практике, как правило, генеральная дисперсия
неизвестна
и
также
подлежит
интервальному
оцениванию.
303.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при известной дисперсии
Пример.
С
надежностью
0,9545
найти
доверительный интервал
для
числа пассажиров
пригородного поезда, если среднее число пассажиров,
рассчитанное за 25 рабочих дней, составляет 512
человек, а дисперсия равна 400.
u 2 x 512
Решение. n 25 400 20
2 20
8.
25
512 8 a 512 8
504 a 520
304.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при неизвестной
дисперсии
. Определим интервальную оценку неизвестной
генеральной средней a нормально распределенной
генеральной совокупности при неизвестной дисперсии.
В отличие от
предыдущего случая, вместо
случайной величины распределенной по стандартному
нормальному закону распределения, рассмотрим
случайную величину (статистику)
x a
x a
,
t
s / n 1 s€/ n
где s2 и ŝ2 соответственно выборочная и
исправленная выборочная дисперсии.
305.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при неизвестной
дисперсии
Представив статистику в виде
x a
t / n ,
1 ns 2
n 1 2
Случайная величина t имеет t-распределение
Стьюдента с k=n-1 степенями свободы, которое не
зависит от неизвестных параметров распределения
случайной величины,
а зависит только от числа
степеней свободы k.
306.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при неизвестной
дисперсии
Для закона распределения Стьюдента составлены
таблицы значений, при которых
P t t ,k .
Следовательно, при оценке генеральной средней
предельная ошибка малой выборки объема n при
t ,n 1 s
неизвестной дисперсии будет равна
,
n 1
а доверительный интервал находиться по формуле
t ,n 1 s
t ,n 1 s
x
a x
.
n 1
n 1
307.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при неизвестной
дисперсии
Если в последних соотношениях выборочную
дисперсию s2 заменить исправленной выборочной
дисперсией ŝ2, то формулы для предельной ошибки
выборки и доверительный интервал будут иметь
следующий вид:
t ,n 1 s€
,
n
t ,n 1 s€
t ,n 1 s€
.
x
a x
n
n
308.
Построение доверительного интервала длягенеральной средней нормально
распределенной генеральной совокупности
по малой выборке при неизвестной
дисперсии
Пример.
С
надежностью
0,95
найти
доверительный интервал
для
числа пассажиров
пригородного поезда, если среднее число пассажиров,
рассчитанное за 25 рабочих дней, составляет 512
человек, а исправленная выборочная дисперсия равна
400.
Решение.
n 25 s€ 400 20 t0,95,24 2,06 x 512
2,06 20
8,245.12 8,24 a 512 8,24
25
503,76 a 520,76
309.
Построение доверительногоинтервала для генеральной
дисперсии
Рассмотрим случайную величину (статистику)
2
ns2
2
.
Можно показать, что такая случайная величина
распределена по закону χ2 с k=n-1 степенями свободы.
Распределение не зависит от неизвестных параметров
случайной величины а зависит лишь от числа степеней
свободы k.
Задаваясь
доверительной
вероятностью
доверительный интервал будем определять из условия:
2
2
ns
2
P лев. 2 прав. .
310.
Построение доверительногоинтервала для генеральной
дисперсии
Графически последнее соотношение означает, что
площадь под кривой функции плотности распределения
2
2
равна γ.
между лев.
и
прав.
Очевидно, что
границы такого
промежутка
определяются
неоднозначно.
Для определенности
будем считать, что
P
2
2
лев.
P
2
2
прав.
1
.
2
311.
Построение доверительногоинтервала для генеральной
дисперсии
Воспользуемся таблицей χ2 распределения:
2
2
прав.
P ,k .
Тогда
P
2
1
.
2
2
1
2
.
,n 1
1 1
1
2
2
1
.
P лев.
2
2
2
2
лев.
2
лев.
2
1
P
2
2
прав.
2
2
.
,n 1
312.
Построение доверительногоинтервала для генеральной
дисперсии
Выражая из двойного неравенства
2
2
лев.
ns
2
2
прав.
неизвестное значение генеральной
получим для нее доверительный интервал:
ns2
2
прав.
s n
прав.
2
ns2
2
лев.
s n .
лев.
.
дисперсии
313.
Построение доверительногоинтервала для генеральной
дисперсии
Пример. По выборке объема 10 из нормально
распределенной генеральной совокупности получено
выборочное значение дисперсии равное 20. Построить
интервальные оценки для генеральной дисперсии и
среднего квадратического отклонения с надежностью
0,95.
Решение.
2
2
2 2
= 2
прав.
=2,7
0,025,9 19.
лев.
1 0 ,95
,9
2
0 ,975,9
10 20
10 20
2
19
2,7
или
10,53 2 74,07.
3,24 8,61.
314.
Спасибо за внимание315.
Анализ данныхАвтор:
доцент департамента
«Анализа данных, принятия решений и финансовых технологий»
к.ф.-м.н.
Потемкин Александр Владимирович
Лекция 9
316.
Анализ данныхЛекция
Проверка статистических гипотез
317.
Статистические гипотезы истатистические критерии
Статистическая гипотеза – это любое
предположение
о
виде
неизвестного
закона
распределения
или
о
параметрах
известных
распределений, проверяемое по выборочным данным.
Примеры.
1.
Генеральная
совокупность распределена по
нормальному закону;
2.
Случайная величина, распределенная по закону
Пуассона, имеет параметр распределения, равный 5;
16.01.2019
118
318.
Статистические гипотезы истатистические критерии
Проверяемую
гипотезу принято называть
нулевой гипотезой и обозначать Н0.
Помимо основной нулевой гипотезы выдвигается
альтернативная гипотеза Н1.
Альтернативная гипотеза всегда
противоречит
нулевой гипотезе или другими словами является
событием несовместным с Н0.
Так, если необходимо выяснить, чему равно
математическое ожидание исследуемого параметра –
двум или трем, то можно проверить нулевую гипотезу
С ей час н е у дает с я от образ и т ь ри с у н ок .
С ей час н е у дает с я от образ и т ь ри с у н ок .
Альтернативной гипотезой будет
319.
Статистические гипотезы истатистические критерии
Вопрос о том, какую гипотезу принять в качестве
альтернативной, как правило, не всегда решается
однозначно.
Для одной и той же нулевой гипотезы можно
рассмотреть несколько альтернативных гипотез.
Так, для рассмотренной выше нулевой гипотезы
можно рассмотреть и другие альтернативы, в
частности, такие как
H 1 : M 2
или
H1 : M 2.
320.
Статистические гипотезы истатистические критерии
Гипотезы о значениях параметров распределения
или о сравнительной величине параметров двух
распределений называются параметрическими, а
гипотезы
о
виде
распределения
называются
непараметическими.
Параметрические гипотезы формулируются на
основании свойств тех или иных статистических
законов распределения и могут использоваться лишь в
том случае, если распределение выборочных данных
согласуется с этим законом распределения.
321.
Статистические гипотезы истатистические критерии
Непараметрические гипотезы применяются в том
случае,
если
закон
распределения
изучаемых
случайных величин неизвестен или их распределение
не соответствует никакому из известных законов.
В этом случае необходимо проверить, согласуются
ли выборочные (эмпирические) данные с каким-либо
теоретическим распределением или нет.
Чаще всего проверяют гипотезу о соответствии
выборочных данных нормальному распределению.
322.
Статистические гипотезы истатистические критерии
Гипотезы подразделяются на простые и сложные.
Простая гипотеза – это гипотеза, которая
содержит только одно предположение.
Например, математическое ожидание нормально
распределенной случайной величины равно 5.
Сложная гипотеза – это гипотеза, которая
состоит из конечного или бесконечного числа простых
гипотез.
Например, математическое ожидание нормально
распределенной случайной величины больше 5.
323.
Статистические гипотезы истатистические критерии
Независимо от наших знаний о генеральной
совокупности, выдвинутая нулевая гипотеза либо верна,
либо неверна.
Проверить нулевую гипотезу означает, что на
основании выборочных данных необходимо ответить на
вопрос, согласуется ли основная гипотеза с опытными
данными или противоречит им.
При этом всегда следует помнить, что любая выборка
содержит в себе ошибку репрезентативности, связанную
с тем, что исследуется не вся генеральная совокупность,
а лишь ее часть.
В связи с этим, по выборке однозначно нельзя
утверждать, что гипотеза верна или неверна, а можно
лишь говорить о том, что согласуется она с опытными
данными или противоречит им.
324.
Статистические гипотезы истатистические критерии
Проверка статистических гипотез осуществляется с
помощью статистических критериев.
Статистический критерий – это случайная
величина (статистика θ), которая представляет собой
функцию, зависящую от выборочных данных, закон
распределения которой (вместе со значениями
параметров) известен в случае, если проверяемая
гипотеза справедлива.
Такой критерий называют критерием согласия,
имея в виду согласие принятой гипотезы с
результатами, полученными по выборке.
Любой статистический критерий устанавливает,
при каких значениях статистики гипотеза принимается,
а при каких она отвергается.
325.
Статистические гипотезы истатистические критерии
Из-за случайности отбора объектов из генеральной
совокупности
в
выборку,
любая
проверка
статистической гипотезы сопряжена с возможностью
допустить некоторые ошибки, что в дальнейшем будет
сопряжено с принятием неправильных решений.
В общем случае с принятием или отклонением
решения возможны два типа ошибок – ошибки первого
и второго рода.
326.
Статистические гипотезы истатистические критерии
Если в действительности гипотеза Н0 верна, а на
основании выборочных данных принято решение ее
отвергнуть, то говорят, что допущена ошибка первого
рода.
С другой стороны, если в действительности верна
альтернативная гипотеза Н1, а принято решение
принять гипотезу Н0 то говорят, что допущена ошибка
второго рода.
Все возможные случаи принятия решения сведены
в таблицу:
327.
Статистические гипотезы истатистические критерии
Определение. Вероятность α ошибки 1-го рода,
т.е. вероятность отвергнуть гипотезу Н0
при
условии, что она верна, называется уровнем
значимости критерия, т.е.
P H1 |H0
Следует
устанавливать
разумные
значения
вероятностей этих ошибок. На практике, обычно
рассматривают значения 0,005, 0,01, 0,05 и 0,1.
При этом следует отметить, что нередко возникают
ситуации, когда одна и та же гипотеза на одном уровне
значимости принимается, а на другом отвергается.
328.
Статистические гипотезы истатистические критерии
Определение. Вероятность
1 ,
противоположная вероятности α, называется
уровнем
доверия,
или
доверительной
вероятностью.
Доверительная вероятность – вероятность принять
нулевую гипотезу при условии, что она верна, т.е.
P H0 | H0
329.
Статистические гипотезы истатистические критерии
Если в действительности верна альтернативная
гипотеза Н1, а принято решение принять гипотезу Н0, то
говорят, что допущена ошибка второго рода.
Вероятность ошибки 2-го рода т.е. вероятность
принять гипотезу Н0 при условии, что она не верна,
обозначается β, т.е.
P H 0 | H1 .
Определение. Вероятность
неверная гипотеза Н0
будет
называется мощностью критерия.
С ей час н е у дает с я от образ и т ь ри с у н ок .
того, что
отвергнута,
330.
Статистические гипотезы истатистические критерии
Естественное желание состоит в том, чтобы
вероятность совершить ошибку первого рода была
минимальной. При этом значение мощность критерия
должна быть как можно больше.
Однако, это противоречивые требования. При
фиксированном объеме выборки можно сделать сколь
угодно малой лишь одну из вероятностей – или .
Уменьшение одной из них сопряжено с
неизбежным увеличением другой. Одновременное
уменьшение вероятностей или возможно только
лишь при изменении объема выборки в сторону его
увеличения.
331.
Статистические гипотезы истатистические критерии
Для любого выбранного статистического критерия
множество всех его возможных значений разделяется
на два непересекающихся подмножества.
Первое подмножество – критическая область –
это множество возможных значений статистического
критерия, при которых нулевая гипотеза отвергается.
Второе подмножество – это множество возможных
значений статистического критерия, при которых
нулевая гипотеза не отвергается.
Вид критической области существенно зависит от
альтернативной гипотезы.
332.
Статистические гипотезы истатистические критерии
Показать критические области можно на графиках
функции распределения статистики критерия.
В зависимости от вида альтернативной гипотезы
различают односторонние и двусторонние (ДКО)
критические области.
Вид
двусторонней
критической
области
следующий:
333.
Статистические гипотезы истатистические критерии
Односторонние критические области также могут
быть либо правосторонние (ПКО), либо левосторонние
(ЛКО).
Точки,
которые
разграничивают критическую
область и область принятия гипотезы, называются
критическими точками.
Критическая область и ее границы полностью
определяются уровнем значимости .
334.
Статистические гипотезы истатистические критерии
Если
закон распределения
статистики
θ,
вычисленной в предположении, что нулевая гипотеза
верна, известен, то критические значения статистики
могут быть найдены из условий:
• для правосторонней критической области
P кр .п . ;
• для левосторонней критической области
P кр .л . ;
• для двусторонней критической области
,
2
P кр.л .
.
2
P кр.п.
335.
Статистические гипотезы истатистические критерии
Общая схема проверки гипотез:
1. В зависимости от задачи
исследования
формулируются статистические – нулевая гипотеза Н0
и альтернативная ей гипотеза Н1.
2. Выбирается
статистическая
характеристика
гипотезы — статистика критерия – случайная величина
θ, распределение которой при справедливости нулевой
гипотезы известно.
3. Задается
уровень
значимости
α
и
рассчитываются границы критической области.
336.
Статистические гипотезы истатистические критерии
Общая схема проверки гипотез:
4. Вычисляется
эмпирическое или наблюдаемое
значение статистики θнабл..
5. Сравнивается
критическое и наблюдаемое
значения статистики и делается вывод.
Если эмпирическое значение статистики θнабл.
(вычисленное по конкретной выборке) попадает в
критическую область, то нулевая гипотеза отвергается
и принимается альтернативная гипотеза; в противном
случае нулевая гипотеза не отвергается.
337.
Гипотезы о числовой величинематематического ожидания нормально
распределенной случайной величины
С проверкой гипотез о числовых значениях каких-либо
величин встречаются довольно часто как в экономических,
так и в физических приложениях.
Например, в финансовом анализе, когда по данным
выборки необходимо установить, можно ли считать
доходность актива определенного вида или портфеля
ценных бумаг, равным заданному числу, или по
результатам
выборочной
аудиторской
проверки
однотипных документов нужно убедиться, можно ли
считать процент допущенных ошибок равным номиналу, и
т.п.
Аналогичные
задачи
могут
возникнуть
и
в
промышленности, например, при проверке качества
функционирования измерительных устройств.
338.
Проверка гипотезы о числовом значенииматематического ожидания при известной
дисперсии
Пусть случайная величина распределена по
нормальному закону с неизвестным математическим
ожиданием и известной дисперсией, т.е.
N a , 2
Формулируется нулевая гипотеза Н0 о том, что
неизвестное математическое ожидание а равно числу
а0, т.е.
H : a a
0
0
339.
Проверка гипотезы о числовомзначении математического
ожидания при известной дисперсии
Для проверки этой гипотезы организуется выборка
из генеральной совокупности объема n.
X1 , X 2 , ..., X n
Каждая варианта выборки распределена по
нормальному закону с теми же самыми параметрами:
В качестве статистики берется величина:
X i N a, 2
x a
.
/ n
Можно показать, что эта статистика будет иметь
стандартное нормальное распределение, т.е.
N 0,1
340.
Проверка гипотезы о числовомзначении математического
ожидания при известной дисперсии
Случайная величина θ зависит только от
выборочных данных.
Для конкретной выборки ее значение будем
называть
эмпирическим
или
наблюдаемым
и
обозначать θнабл..
При проверке нулевой гипотезы Н0: а=а0,
вычисляется по формуле:
x a0
набл.
/ n
θнабл.
.
Согласно общей схеме проверки гипотез, далее
необходимо выдвинуть альтернативную гипотезу.
341.
Проверка гипотезы о числовомзначении математического
ожидания при известной дисперсии
Относительно ее формулировки можно выделить
три различных случая.
H1: a a1 a0 ;
H1: a a1 a0 ;
H1: a a1 a0 .
342.
Проверка гипотезы о числовомзначении математического
ожидания при известной дисперсии
1. В случае альтернативной гипотезы
H1: a a1 a0
критическая область будет правосторонней и
представляет собой интервал
Граница критической области определяется из
P кр .пр . .
условия:
Используя связь функции распределения с
функцией
Лапласа,
последнюю
вероятность
представим в виде:
С ей час н е у дает с я от образ и т ь ри с у н ок .
P кр .пр. 1 P кр .пр. 1 FN кр .пр. 1
1
1 2Ф кр .пр.
2
.
343.
Проверка гипотезы о числовомзначении математического
ожидания при известной дисперсии
Разрешая последнее соотношение относительно
функции Лапласа, получим:
1
Ф кр .пр . .
2
Используя таблицу значений функции Лапласа
Ф( х )
1
x
t 2
e dt
2
2
0
находим ее аргумент, соответствующий значению
вероятности 1/2 −







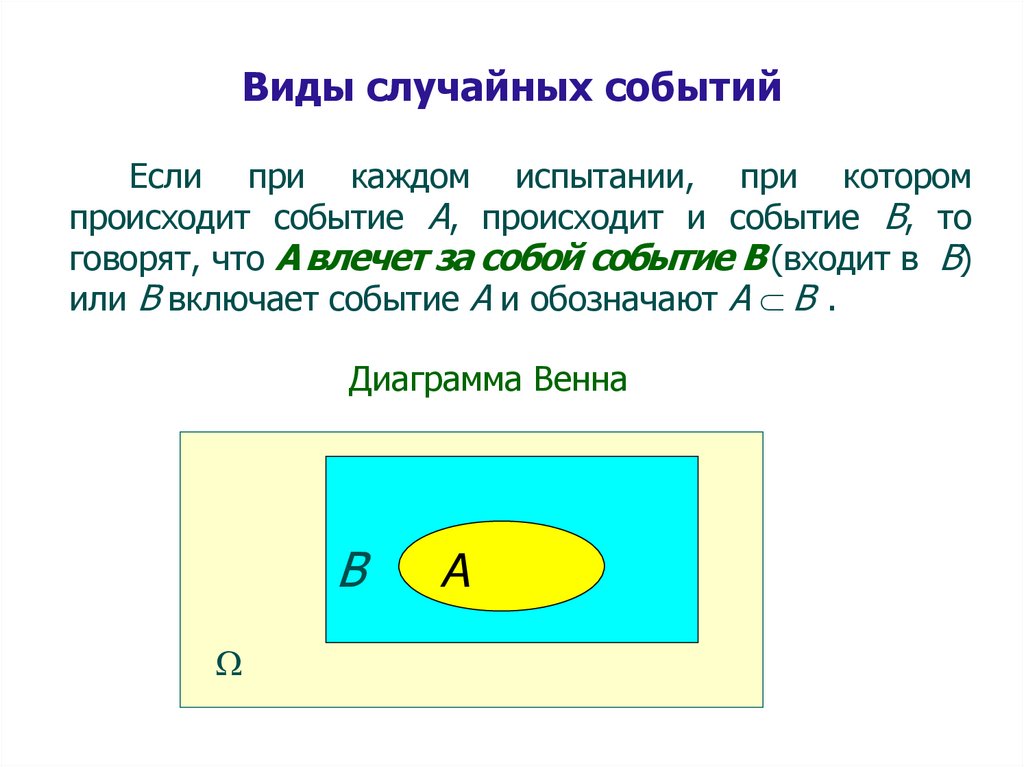



































































































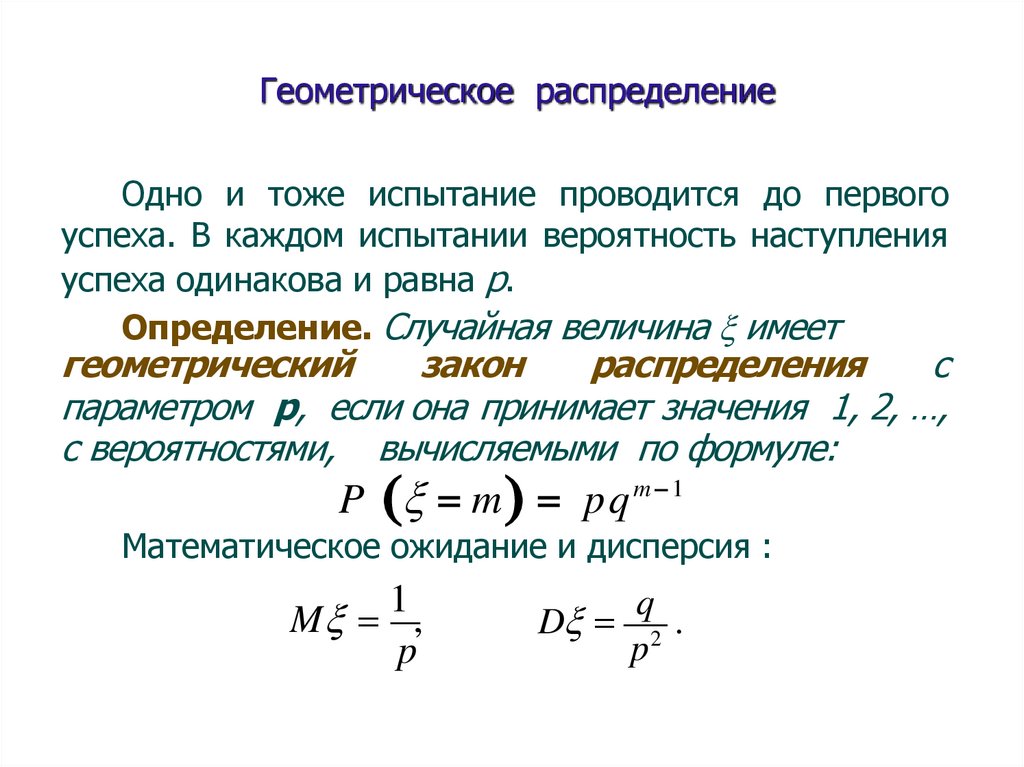














































































































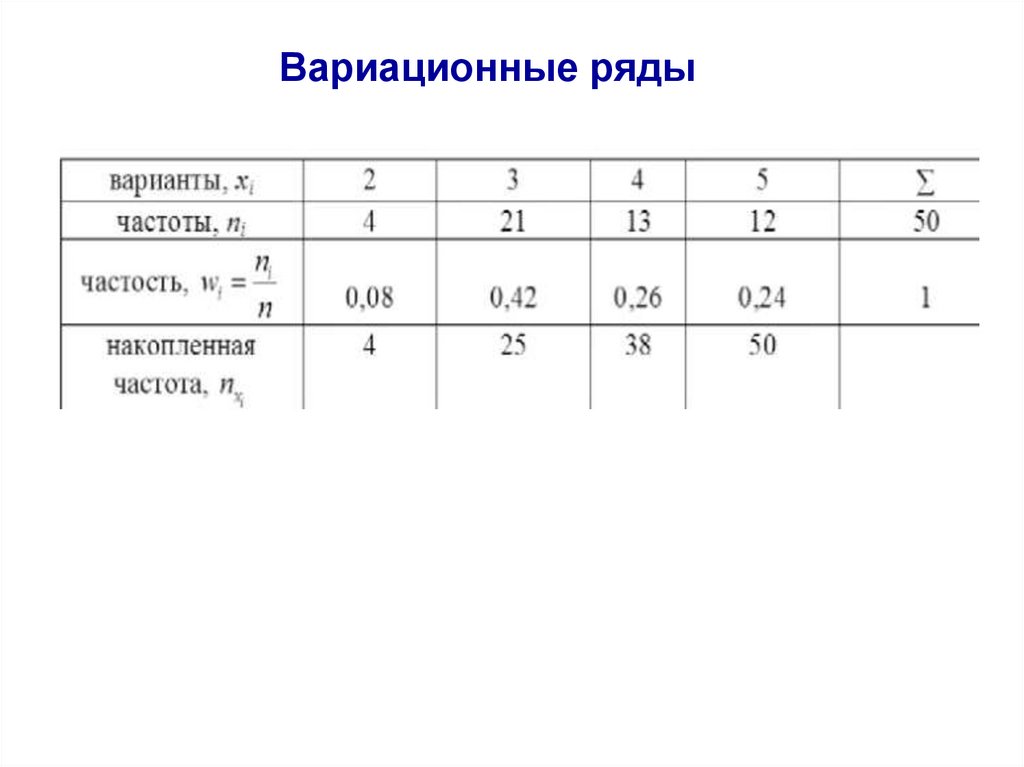













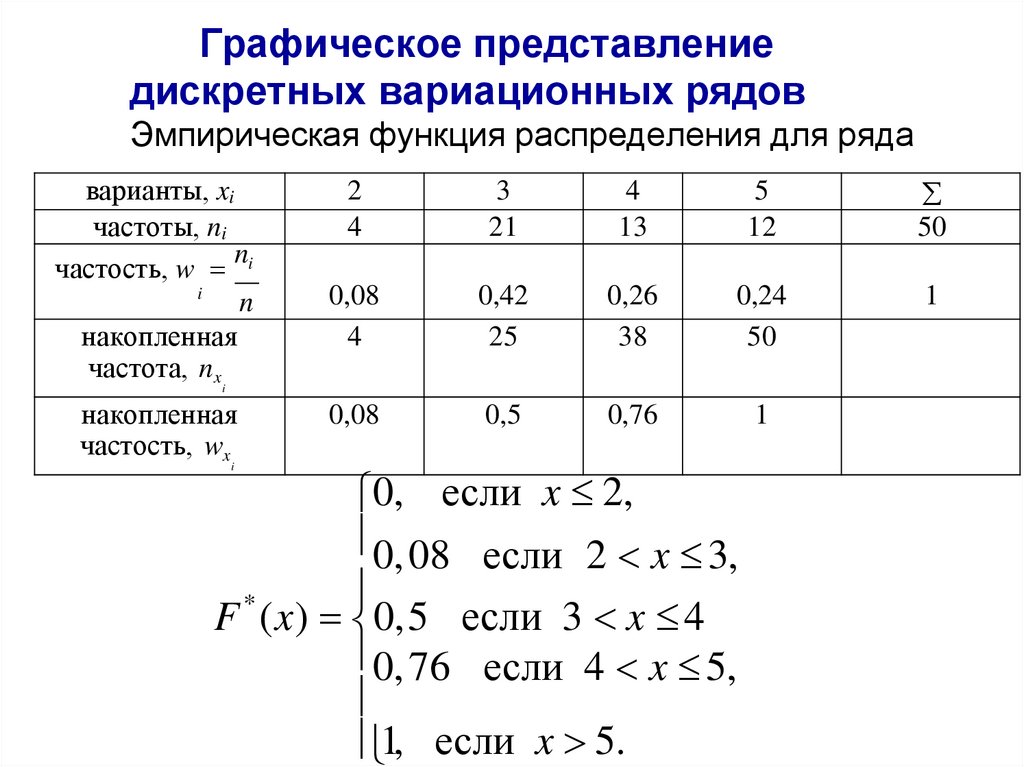

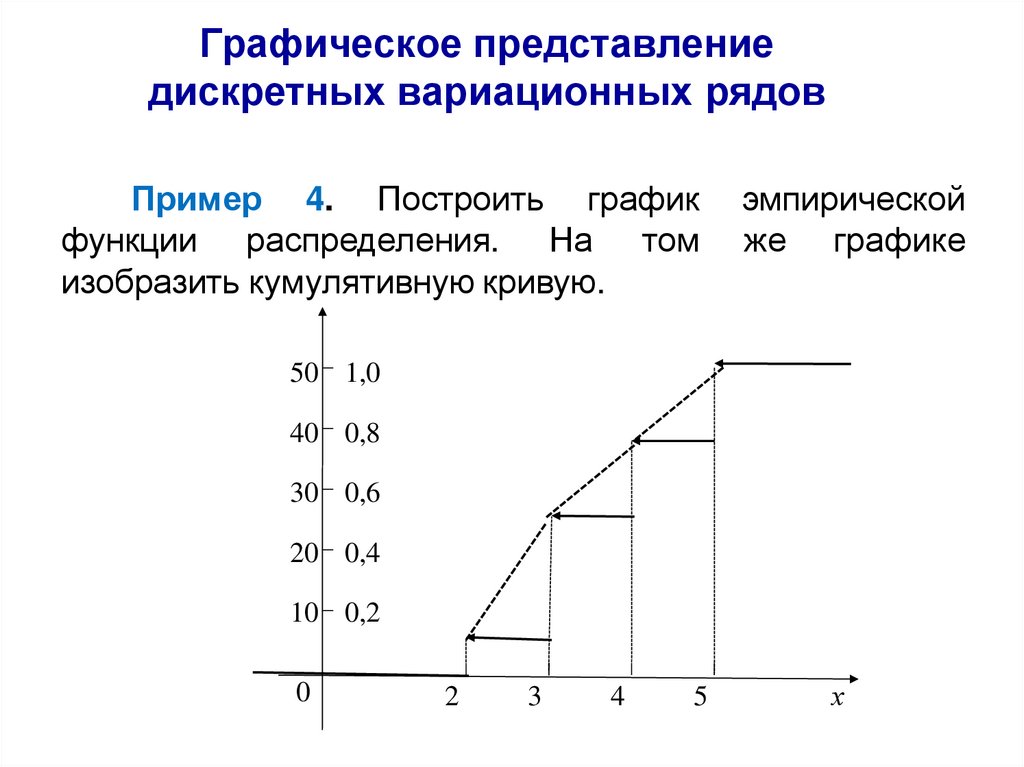















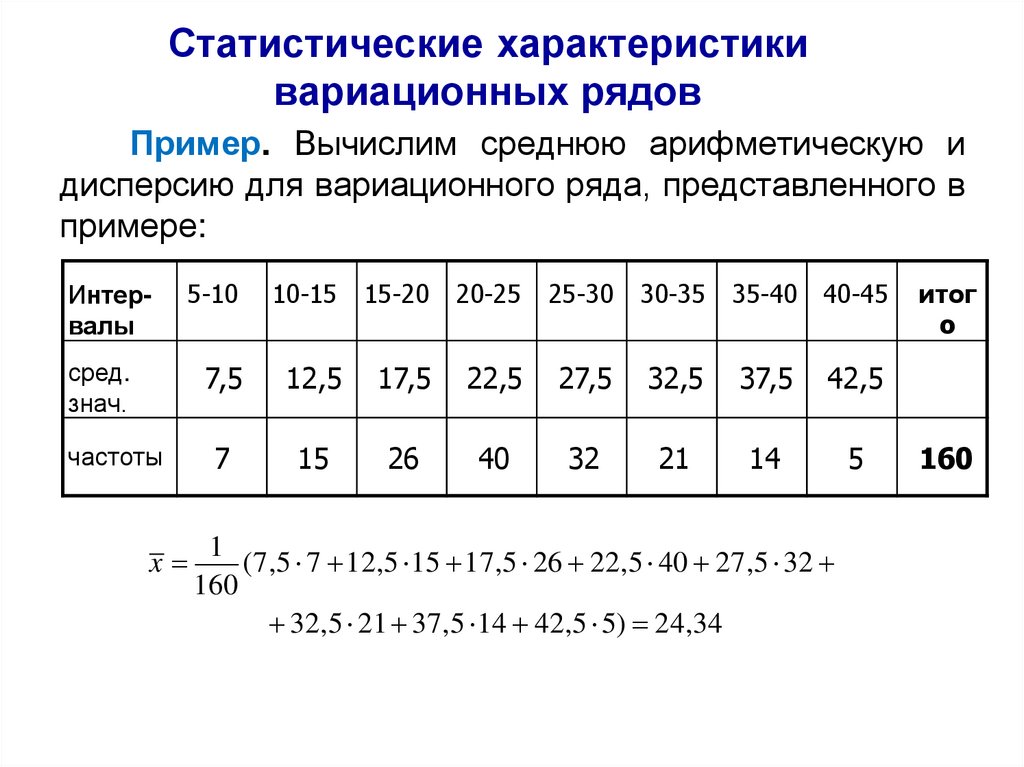









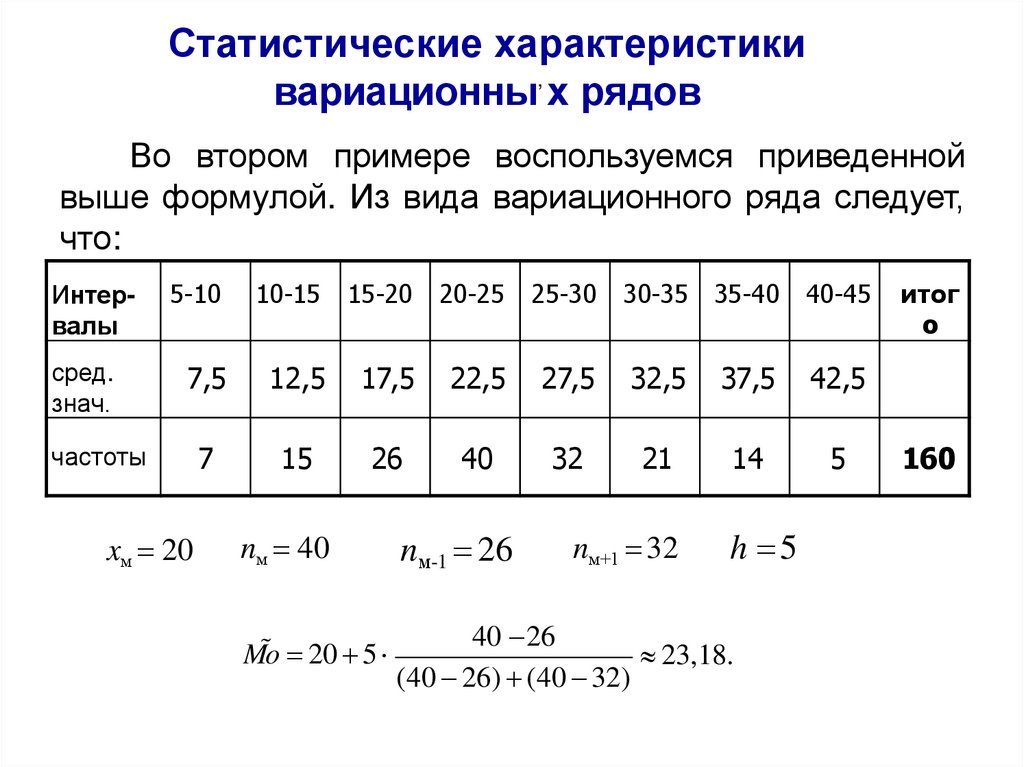


















































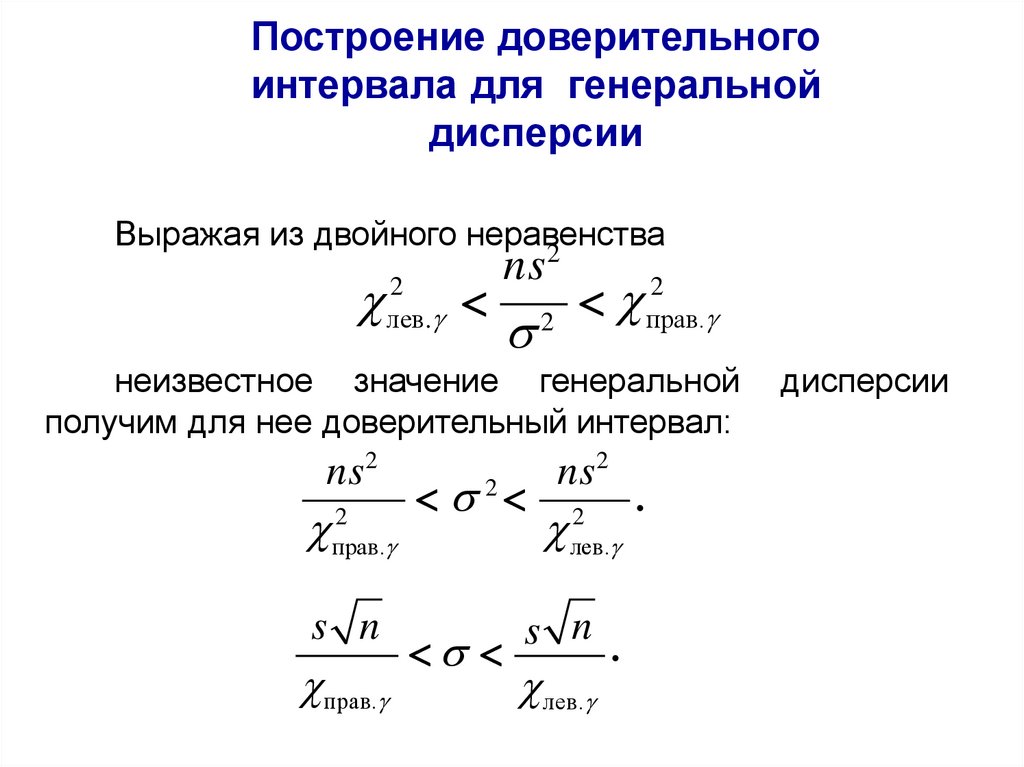



















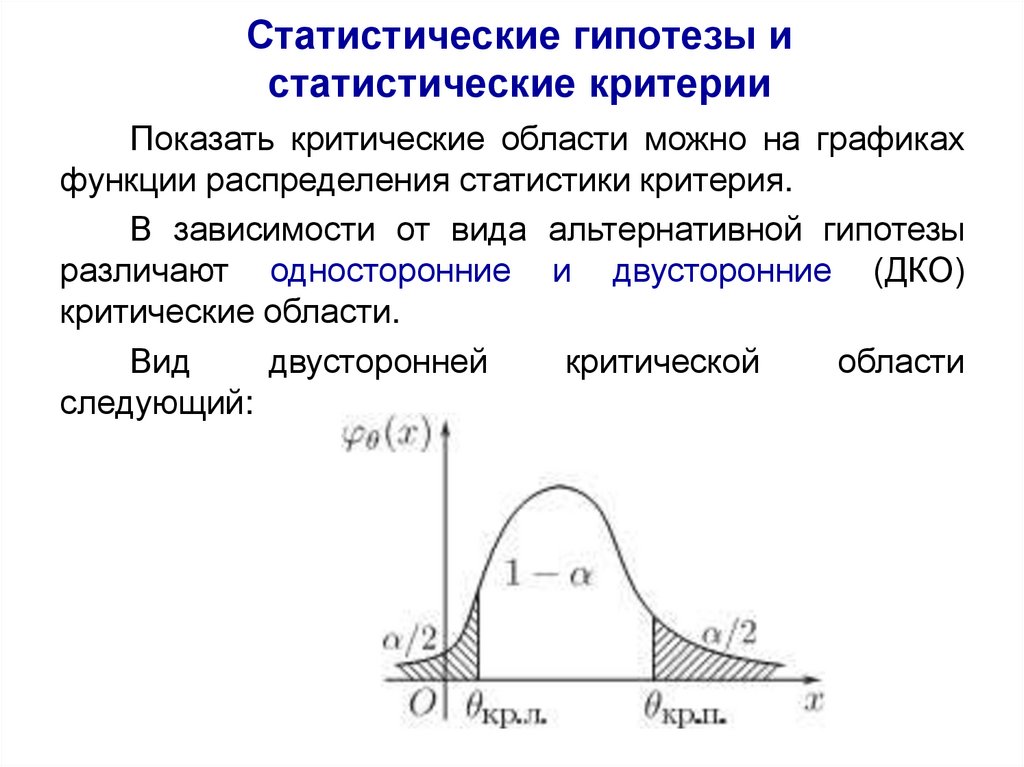

















































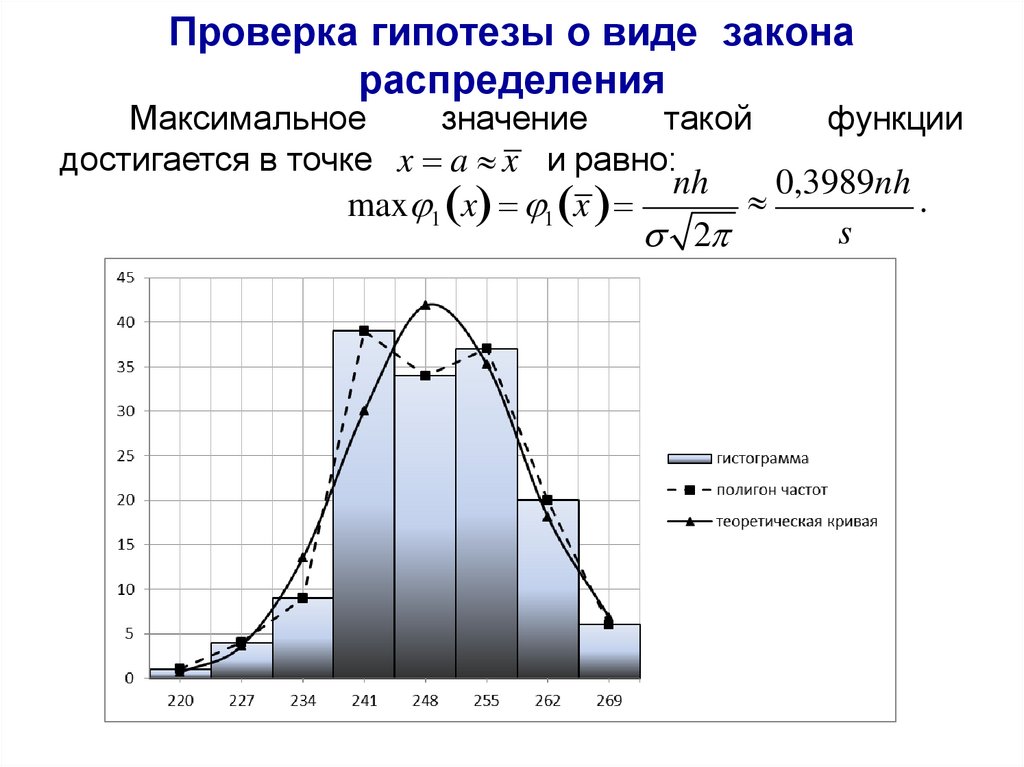












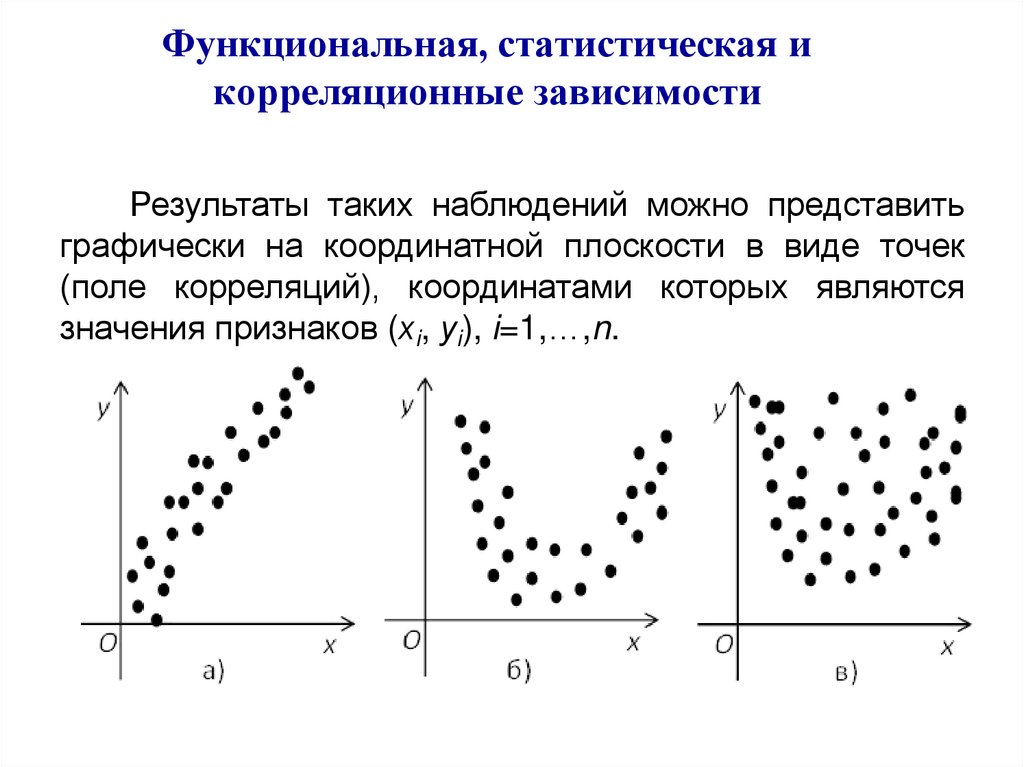





























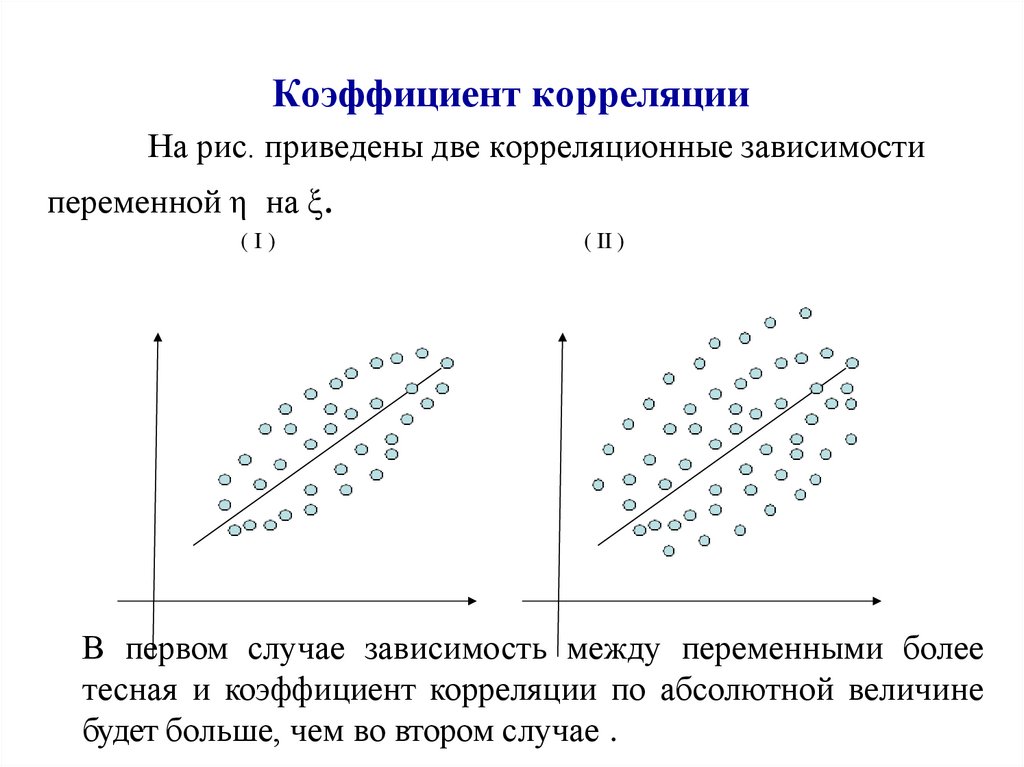






 mathematics
mathematics