Similar presentations:
Высшая математика. § 5. Решение СЛУ по формулам Крамера
1. Высшая математика 1 семестр Лекция 2
ЗТЭ-221, ЗЭМ-221Л.В. Бельгарт
1
2. § 5. Решение СЛУ по формулам Крамера
Рассмотрим систему n линейных уравненийс n неизвестными
a11 x1 a12 x2
a x a x
21 1 22 2
an1 x1 an 2 x2
2
a1n xn b1
a2 n xn b2
an n xn bn
3
3. Теорема
Если определитель основной матрицысистемы (3) отличен от нуля, то система (3)
является определённой. Решение находится по
формулам Крамера
1
2
x1 , x2
,
3
n
, xn .
где k – получается из определителя основной
матрицы системы (3) заменой k-го столбца
столбцом свободных членов.
4. Пример 3
Решить СЛУ по формулам Крамера2 x1 5 x2 3x3 4
3x1 4 x2 2 x3 0
4x
5 x3 3
1
4
5. Пример 3
2 x1 5 x2 3x3 43x1 4 x2 2 x3 0
4x
5 x3 3
1
2 5 3
3 4 2 40 40 0 48 75 0 43
4 0 5
5
6. Пример 3
2 x1 5 x2 3x3 43x1 4 x2 2 x3 0
4x
5 x3 3
1
2 5 3
3 4 2 40 40 0 48 75 0 43
4 0 5
4 5 3
1 0 4 2 80 30 0 36 0 0 86
3 0 5
6
7. Пример 3
2 x1 5 x2 3x3 43x1 4 x2 2 x3 0
4x
5 x3 3
1
2 5 3
3 4 2 40 40 0 48 75 0 43
4 0 5
2 4 3
2 3 0 2 0 32 27 0 12 60 43
4 3 5
7
8. Пример 3
2 x1 5 x2 3x3 43x1 4 x2 2 x3 0
4x
5 x3 3
1
2 5 3
3 4 2 40 40 0 48 75 0 43
4 0 5
2 5 4
3 3 4 0 24 0 0 64 45 43
4 0 3
8
9. Пример 3
1 86x1
2
43
2 43
x2
1
43
3 43
x3
1
43
9
2 x1 5 x2 3x3 4
3x1 4 x2 2 x3 0
4x
5 x3 3
1
10. Пример 3
2 x1 5 x2 3x3 43x1 4 x2 2 x3 0
4x
5 x3 3
1
x1 2, x2 1, x3 1
Проверка: 1) 4 5 3 4
верное
2) 6 4 2 0
3) 8 5 3
Ответ: x1 2, x2 1, x3 1
10
11. § 6. Решение СЛУ методом Гаусса
12. Элементарные преобразования строк матрицы
перестановка местами строк;умножение всех элементов строки на одно
и то же число, отличное от нуля;
прибавление элементов какой-либо строки
к соответствующим элементам другой
строки, умноженных на одно и то же число;
вычёркивание нулевой строки или одной
из двух пропорциональных или одной из
двух равных.
13. Определение
Две матрицы A и B называютсяэквивалентными, если одна из них
получается из другой с помощью
элементарных преобразований.
Обозначения: A B.
14. Замечание 1
Элементарныепреобразования
меняют ранга матрицы
не
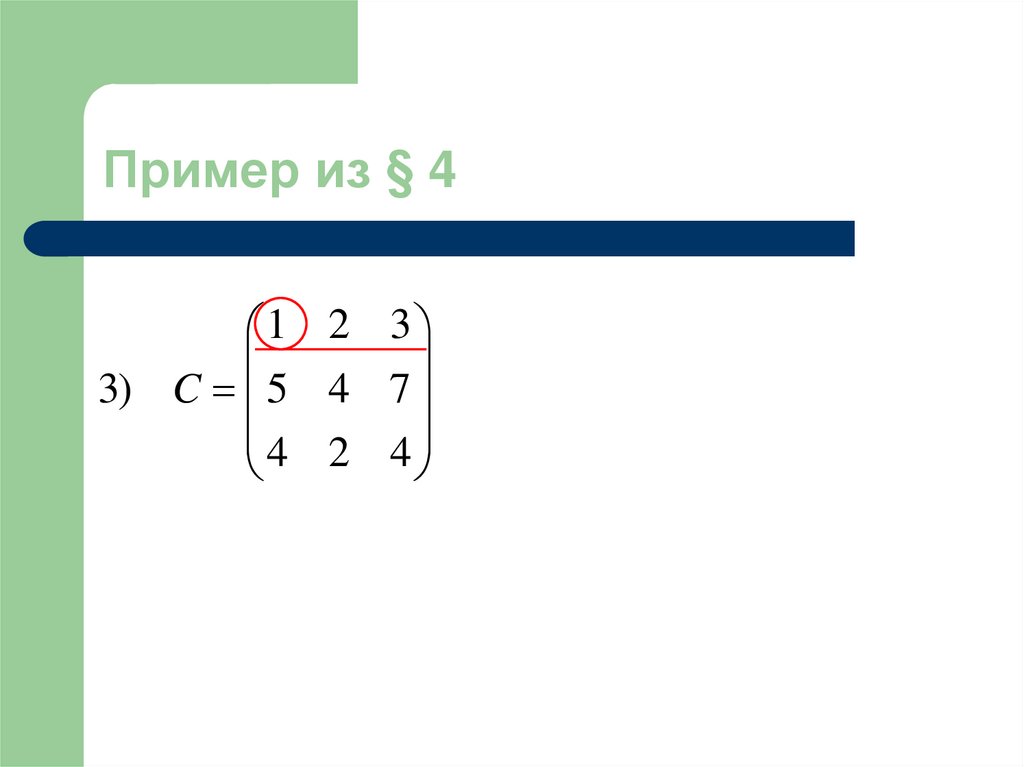
15. Пример из § 4
Найти ранг матрицы с помощьюэлементарных преобразований
1 2 3
3) C 5 4 7
4 2 4
16. Пример из § 4
1 2 33) C 5 4 7
4 2 4
17. Пример из § 4
1 2 3 53) C 5 4 7
4 2 4
1
2
3
18. Пример из § 4
1 2 3 53) C 5 4 7
4 2 4
1 2 3
0 6 8
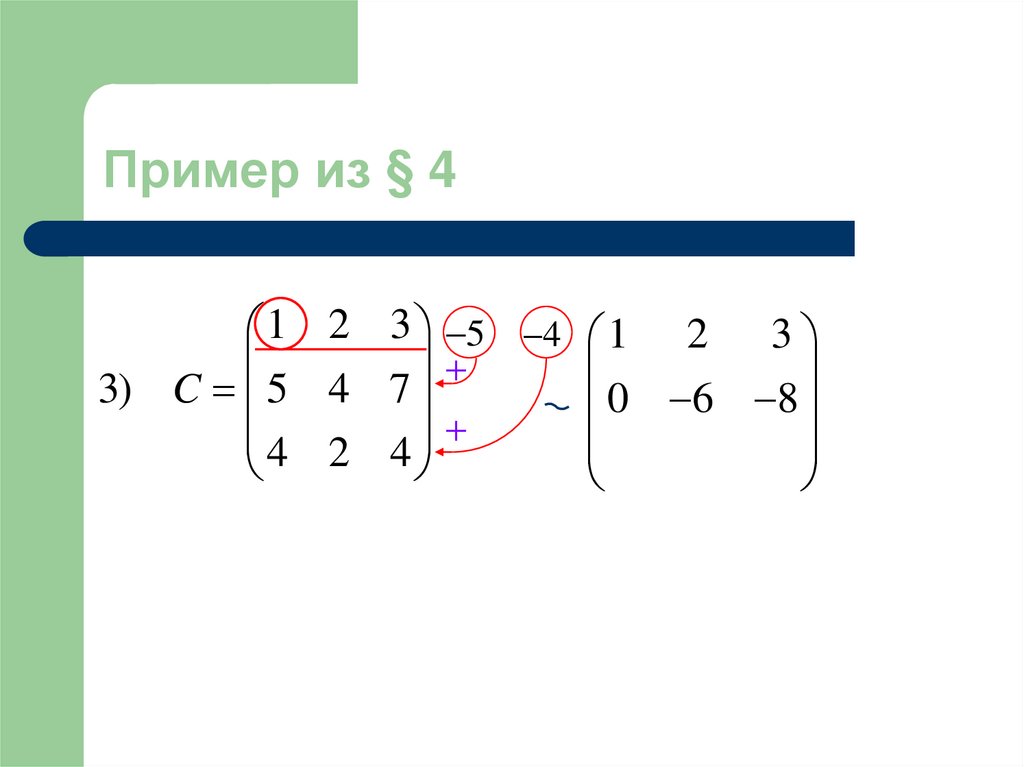
19. Пример из § 4
1 2 3 5 4 1 2 30 6 8
3) C 5 4 7
4 2 4
20. Пример из § 4
1 2 3 5 43) C 5 4 7
4 2 4
1 2 3
0 6 8
0 6 8
21. Пример из § 4
1 2 3 5 43) C 5 4 7
4 2 4
1 2 3
0 6 8
1 2 3
0 6 8
0 6 8
22. Пример из § 4
1 2 3 5 43) C 5 4 7
4 2 4
1 2 3
0 6 8
0 6 8
1 2 3
0 6 8 ; 2 6 0
23. Пример из § 4
1 2 3 5 43) C 5 4 7
4 2 4
1 2 3
0 6 8
0 6 8
1 2 3
0 6 8 ; 2 6 0; r C 2.
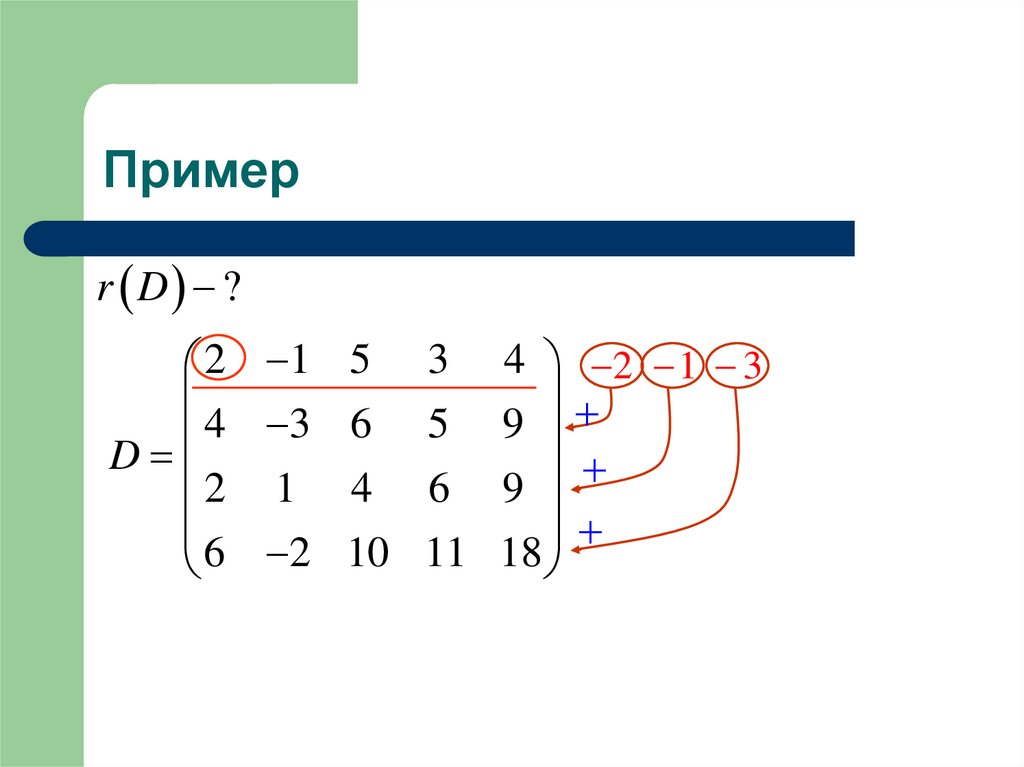
24. Пример
r D ?25. Пример
r D ?2 1
4 3
D
2 1
6 2
5
6
4
10
3
5
6
11
4
9
9
18
26. Пример
r D ?2 1
4 3
D
2 1
6 2
5
6
4
10
3
5
6
11
4 2 1 3
9
9
18
27. Пример
r D ?2 1
4 3
D
2 1
6 2
5
6
4
10
3
5
6
11
4
9
9
18
2 1 5 3
0 1 4 1
0 2 1 3
0 1 5 2
4
1
5
6
28. Пример
2 1 5 30 1 4 1
0 2 1 3
0 1 5 2
4
1
5
6
2 1 5 3
0 1 4 1
0 0 9 1
0 0 9 1
4
1
7
7
29. Пример
2 1 5 30 1 4 1
0 0 9 1
0 0 9 1
4
1
7
7
2 1 5 3
0 1 4 1
0 0 9 1
0 0 0 0
4
1
7
0
30. Пример
2 1 5 30 1 4 1
0 0 9 1
0 0 0 0
4
1
7
0
r D 3
31.
2Метод Гаусса наиболее универсальный
метод
решения
СЛУ,
состоит
в
последовательном исключении переменных
и происходит в два этапа.
Пусть дана система (2) § 4.
32. § 4. Системы линейных уравнений (СЛУ)
Рассмотрим систему, содержащую mлинейных уравнений с n неизвестными
a11 x1 a12 x2
a x a x
21 1 22 2
am1 x1 am 2 x2
a1n xn b1
a2 n xn b2
am n xn bn
2
33.
2Пусть дана система (2) § 4.
На первом этапе (прямой ход) система
приводится к ступенчатому виду
(треугольному или к виду трапеции)
34.
2a11 x1 a12 x2 a1r xr
a22 x2 a2 r xr
arr xr
r n, aii 0, i 1, 2,
a1n xn b1
a2 n xn b2
arn xn br
, r.
35.
2Переменные
x1 , x2 ,
, xr
базисными,
остальные переменные xr 1 ,
называются свободными.
называются
, xn
36.
2На втором этапе (обратный ход) идёт
последовательное определение
переменных из ступенчатой системы.
37. Замечание 2
На практике удобно работать не ссистемой (2) § 4, а с расширенной матрицей
системы, выполняя над её строками
элементарные преобразования.
38. Замечание 3
Возможны три случая. Рассмотрим их насхемах системы 3-х уравнений с тремя
неизвестными.
39. Замечание 3
Возможны три случая. Рассмотрим их насхемах системы 3-х уравнений с тремя
неизвестными.
После элементарных преобразований:
40. Замечание 3
00 0
Треугольная
r A r A 3
Совместная
n r 3
Определённая
Система имеет
ед-ое решение
0
0 0 0 0
Вид трапеции
r A r A 2
0
0 0 0
Вид трапеции
r A 2,
Совместная
r A 3
n 3 r Неопр. Несовместная
Беск. много реш. Система
n r 3 2 1
не имеет
Одна своб. перем решений
41. Пример
Решить методом Гаусса СЛУ2 x1 x2 3x3 5 x4 1
x x 5x 2
1 2
3
3x1 2 x2 2 x3 5 x4 3
4 x1 3x2 7 x3 5 x4 5
42. Пример
Решить методом Гаусса СЛУ2 x1 x2 3x3 5 x4 1
x x 5x 2
1 2
3
3x1 2 x2 2 x3 5 x4 3
4 x1 3x2 7 x3 5 x4 5
2
1
3
4
1 3 5
1 5 0
2 2 5
3 7 5
1
2
3
5
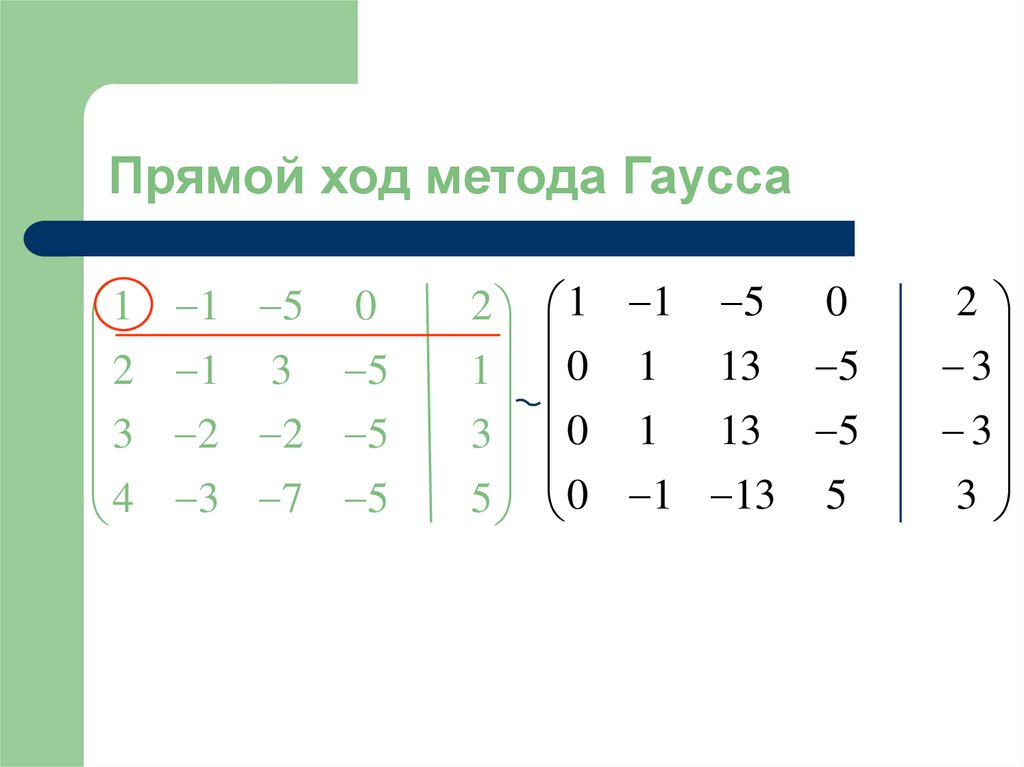
43. Прямой ход метода Гаусса
21
3
4
1 3 5
1 5 0
2 2 5
3 7 5
1
2
3
5
1
2
3
4
1 5 0
1 3 5
2 2 5
3 7 5
1
2
3
5
44. Прямой ход метода Гаусса
12
3
4
1 5 0
1 3 5
2 2 5
3 7 5
2
1
3
5
1 1 5 0
0 1 13 5
0 1 13 5
0 1 13 5
2
3
3
3
45. Прямой ход метода Гаусса
1 1 5 00 1 13 5
0 1 13 5
0 1 13 5
2
3
3
3
1 1 5 0
0 1 13 5
0 0 0 0
0 0 0 0
2
3
0
0
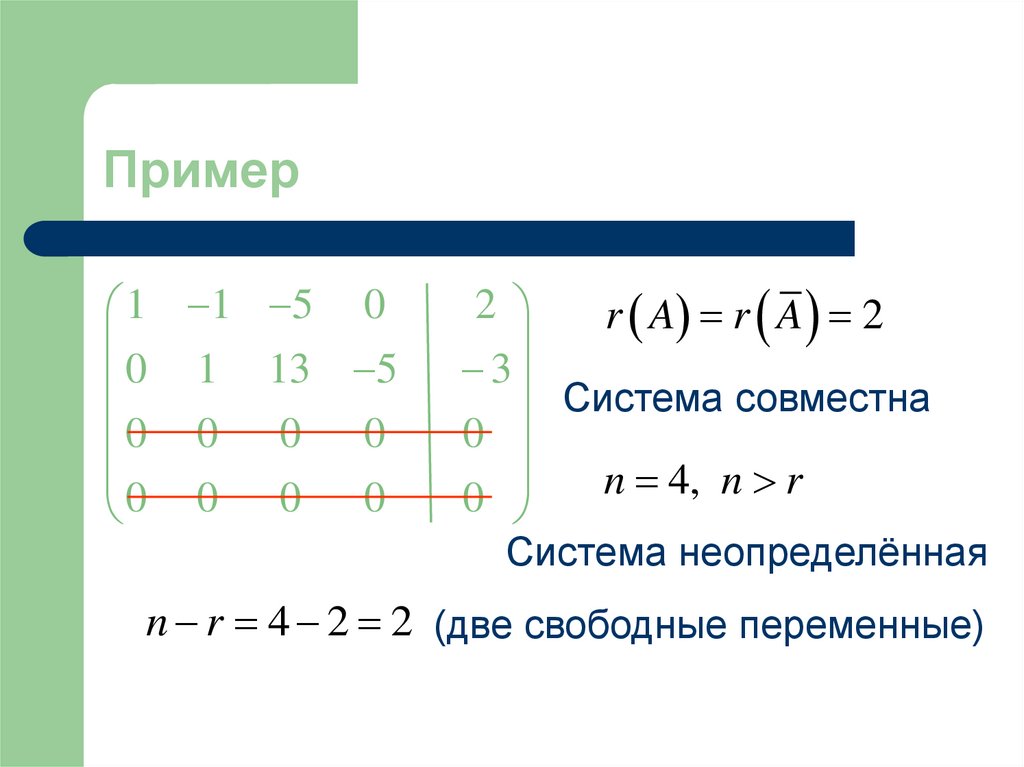
46. Пример
1 1 5 00 1 13 5
0 0 0 0
0 0 0 0
2
r A r A 2
3
Система совместна
0
n 4, n r
0
Система неопределённая
n r 4 2 2 (две свободные переменные)
47. Обратный ход метода Гаусса
1 1 5 00 1 13 5
0 0 0 0
0 0 0 0
2
3
0
0
x3 R, x4 R
x2 13x3 5 x4 3 x2 3 13x3 5 x4
48. Обратный ход метода Гаусса
21 1 5 0
0 1 13 5 3
0
0 0 0 0
0
0
0
0
0
x3 R, x4 R
x2 13x3 5 x4 3 x2 3 13x3 5 x4
x1 x2 5 x3 2 x1 2 x2 5 x3
49. Обратный ход метода Гаусса
21 1 5 0
0 1 13 5 3
0
0 0 0 0
0
0
0
0
0
x3 R, x4 R
x2 13x3 5 x4 3 x2 3 13x3 5 x4
x1 x2 5 x3 2 x1 2 x2 5 x3
x1 2 3 13x3 5 x4 5 x3 1 8 x3 5 x4
50. Проверка
x1 1 8 x3 5 x4x2 3 13x3 5 x4
x3 R, x4 R
Для проверки найдём одно частное решение.
Пусть x3 1, x4 1 , тогда x1 2, x2 5.
51. Проверка
2 x1 x2 3x3 5 x4 1x x 5x 2
1 2
3
Проверка 3x1 2 x2 2 x3 5 x4 3
4 x1 3x2 7 x3 5 x4 5
Для проверки найдём одно частное решение.
Пусть x3 1, x4 1 , тогда x1 2, x2 5.
верное
1) 4 5 3 5 1
2) 2 5 5 2
3) 6 10 2 5 3
4) 8 15 7 5 5
52. Ответ
x1 1 8 x3 5 x4x 3 13x 5 x
2
3
4
x3 R
x4 R
53. § 7. Линейные операции над матрицами
1A B. Складывать можно матрицы только
одинакового размера.
Опр. Суммой двух матриц Am n ai j и Bm n bi j
называется матрица Cm n ci j такая,
что c a b
i 1, m, j 1, n .
ij
53
ij
ij
54. Пример
1Пример
2 3 2 4 2 1
4 5 1 3 2 0
54
55. Пример
1Пример
2 3 2 4 2 1 6
4 5 1 3 2 0
55
.
56. Пример
1Пример
2 3 2 4 2 1 6 5
4 5 1 3 2 0
56
.
57. Пример
1Пример
2 3 2 4 2 1 6 5 1
4 5 1 3 2 0
.
57
58. Пример
1Пример
2 3 2 4 2 1 6 5 1
4 5 1 3 2 0 1
.
58
59. Пример
1Пример
2 3 2 4 2 1 6 5 1
4 5 1 3 2 0 1 7
.
59
60. Пример
1Пример
2 3 2 4 2 1 6 5 1
4 5 1 3 2 0 1 7 1 .
60
61. § 7. Линейные операции над матрицами
2 k A.Опр.
61
Произведением матрицы Am n ai j
на число k называется матрица Bm n bi j
такая, что bi j k ai j i 1, m, j 1, n .
62. Пример
262
3
5
2 A 2 2 1
7 4
63. Пример
263
3 10
5
2 A 2 2 1
7 4
64. Пример
264
3 10
5
2 A 2 2 1
7 4
6
65. Пример
265
3 10
5
2 A 2 2 1 4
7 4
6
66. Пример
266
3 10
5
2 A 2 2 1 4
7 4
6
2
67. Пример
267
3 10
5
2 A 2 2 1 4
7 4 14
6
2
68. Пример
268
3 10 6
5
2 A 2 2 1 4 2
7 4 14 8
69. § 7. Линейные операции над матрицами
369
Опр.
Матрица A называется
противоположной матрице A.
70. Свойства линейных операций
3Свойства линейных операций
1 . A B B A
70
71. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
71
72. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
2 . A B C A B C ассоциативность,
72
73. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
2 . A B C A B C ассоциативность,
3 . A O A
73
74. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
2 . A B C A B C ассоциативность,
3 . A O A
4 . A A O
74
75. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
2 . A B C A B C ассоциативность,
3 . A O A
4 . A A O
5 . k A B k A k B дистрибутивность
относительно суммы матриц,
75
76. Свойства линейных операций
3Свойства линейных операций
1 . A B B A коммутативность,
2 . A B C A B C ассоциативность,
3 . A O A
4 . A A O
5 . k A B k A k B дистрибутивность
относительно суммы матриц,
6 . k1 k2 A k1 A k2 A дистрибутивность
относительно суммы чисел
76
77. Свойства линейных операций
3Свойства линейных операций
7 . k1 k2 A k1k2 A ассоциативность
относительно умножения чисел
T
T
T
8 . A B A B
77
78. § 8. Произведение матриц
79. § 8. Произведение матриц
Операция умножения двух матриц вводитсятолько для случая,
80. § 8. Произведение матриц
Операция умножения двух матриц вводитсятолько для случая, когда число столбцов
первой матрицы совпадает с числом строк
второй матрицы.
81. Определение
Произведением матрицы Am p ai k наматрицу B p n bk j называется матрица
Cm n ci j такая, что
p
ci j ai k bk j i 1, m, j 1, n
k 1
т.е. элемент i -ой строки и j -го столбца
матрицы C равен сумме произведений
элементов i -ой строки первой матрицы A и
соответствующих элементов j -го столбца
второй матрицы B .
82. Пример
Найти произведение матриц AB и BA,где
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
83.
AB ? BA ?A2 3 B3 2
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
84.
AB ? BA ?A2 3 B3 2 AB 2 2
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
85.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
1 3 2
AB
1
2
2
5
3
1 4
86.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
1 3 2
AB
1
2
2
5
3
1 4
87.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
1 3 2
2 3 2
AB
1
2
2
5
3
1 4
88.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
1 3 2
2 3 2 5 6 8
AB
1
2
2
5
3
1 4
89.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
1 3 2
2 3 2 5 6 8
AB
1
2
2
5
3
4
5
3
1 4
90.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
5 6 8
1 3 2
2 3 2
AB
1
2
2
5
3
4
5
3
10
10
12
1 4
91.
AB ? BA ?5.
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
5 6 8
1 3 2
2 3 2
AB
1
2
2
5
3
4
5
3
10
10
12
1 4
3 7
4 12
92.
AB ? BA ?5.
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
A2 3 B3 2 AB 2 2
2 5
5 6 8
1 3 2
2 3 2
AB
1
2
2
5
3
4
5
3
10
10
12
1 4
3 7
4 12
93.
AB ? BA ?B3 2 A2 3 BA 3 3
2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
94.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
B3 2 A2 3 BA 3 3
2 5
1 3 2
BA 1 2
2 5 3
1 4
95.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10
96.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25
97.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
98.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4
99.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4 3 10
100.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4 3 10 2 6
101.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4 3 10 2 6
1 8
102.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4 3 10 2 6
1 8 3 20
103.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15
1 4 3 10 2 6
1 8 3 20 2 12
104.
AB ? BA ?2 5
1 3 2
1
A
,
B
2
2
5
3
1 4
2 5
1 3 2
BA 1 2
2 5 3
1 4
2 10 6 25 4 15 12 31 19
1 4 3 10 2 6 5 13 8
1 8 3 20 2 12 7 17 10
105. Спасибо за внимание
105





















































































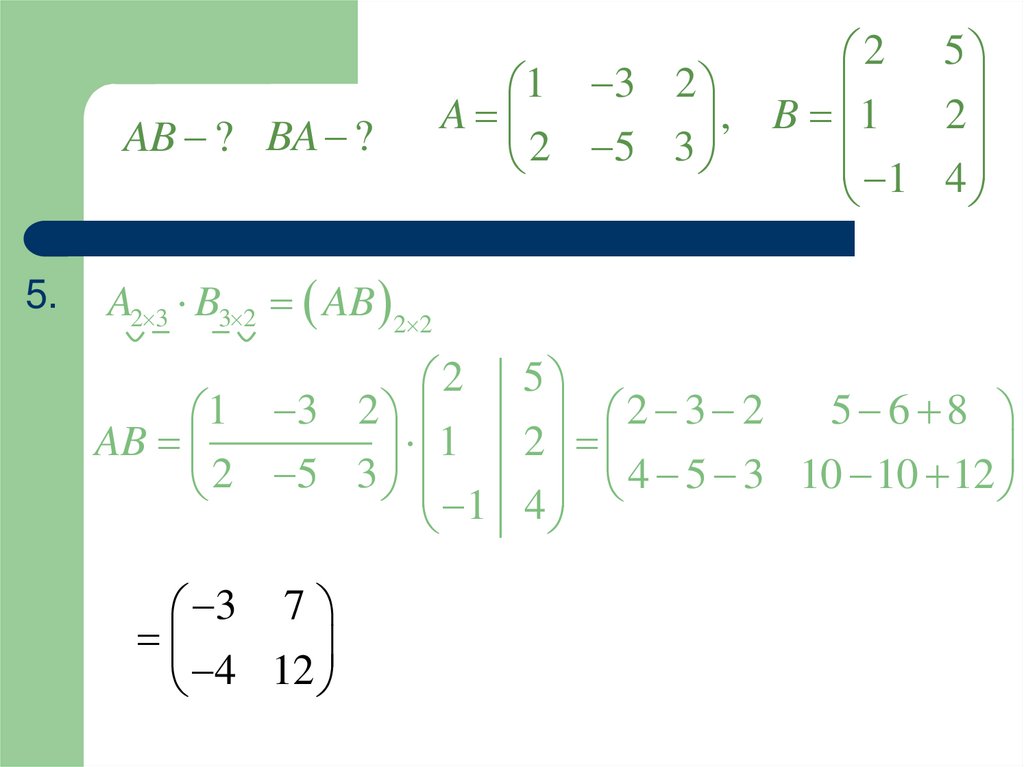












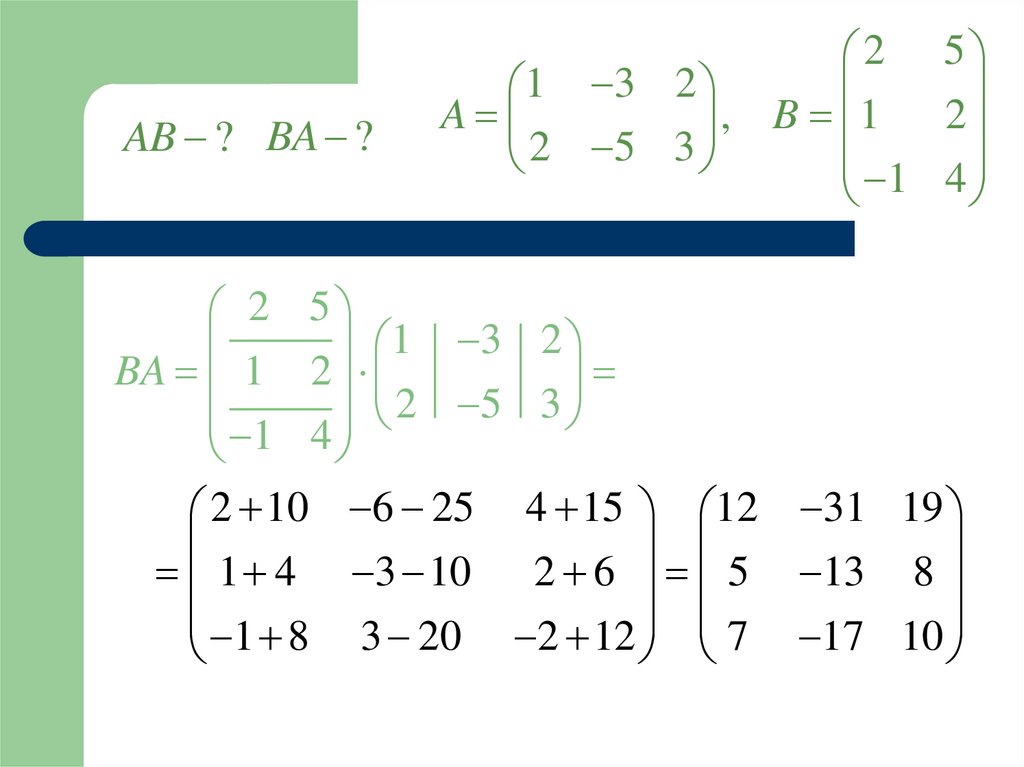

 mathematics
mathematics








