Similar presentations:
Аналитическая геометрия на плоскости
1. Аналитическая геометрия на плоскости Прямая на плоскости 1. Различные способы задания прямой. 2. Взаимное расположение прямых.
3. Угол между прямыми.4. Расстояние от точки до прямой
Кривые второго порядка
1. Эллипс
2. Гипербола
3. Парабола
1
2.
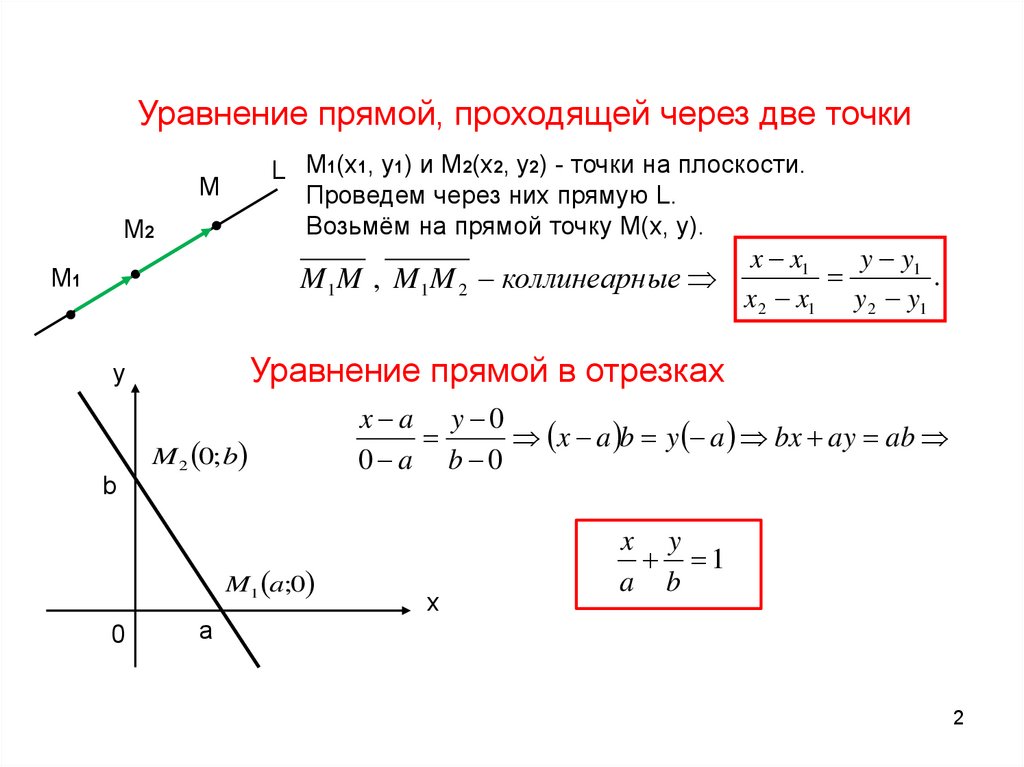
Уравнение прямой, проходящей через две точкиL М1(x1, y1) и M2(x2, y2) - точки на плоскости.
Проведем через них прямую L.
Возьмём на прямой точку M(x, y).
M
M2
M 1M , M 1M 2 коллинеарн ые
M1
x x1
y y1
.
x2 x1 y 2 y1
Уравнение прямой в отрезках
y
M 2 0; b
x a y 0
x a b y a bx ay ab
0 a b 0
b
M1 a;0
0
а
x
x y
1
a b
2
3.
Каноническое уравнение прямойa
М0
Прямая L однозначно может быть задана
М
L
точкой М(x0, y0) и вектором а m ; n ,
Возьмём на прямой точку M(x, y).
M 0 M , а коллинеарные
x x0 y y 0
.
m
n
3
4.
Параметрические уравнения прямойx x0 y y0
t
m
n
x x0 mt,
y y0 nt.
Уравнение прямой, заданной точкой и вектором нормали
L
n
M0
M
Задана точка М0(x0, y0) и вектор нормали n A; B .
М(x, y) – произвольная точка на прямой L.
M0M n n M0M 0
A( x x0 ) B( y y0 ) 0.
4
5.
Общее уравнение прямойA( x x0 ) B( y y0 ) 0
Ax Ax0 By By 0 0,
Ax By ( Ax0 By 0 ) 0,
Ax By C 0.
Уравнение прямой, заданной точкой
и угловым коэффициентом
y
М
y
М0
y0
Из M 0 MA tg
A
0
Задана точка М0(x0, y0) и
угловой коэффициент k tg .
М(x, y) – произвольная точка на прямой L.
L
x
x0
x
y y0
,
x x0
y y0 k ( x x0 ).
5
6.
Уравнение прямой с угловым коэффициентомy y0 k ( x x0 )
y y0 kx kx0 ,
y kx ( y0 kx0 ),
y kx b
Расстояние от точки до прямой
М0
d
Задана точка М0(x0, y0) и
прямая
Ax By C 0.
Расстояние от точки до прямой
вычисляется по формуле:
d
Ax0 By 0 C
A2 B 2
6
7.
78. Угол между прямыми
89.
910. Кривые второго порядка Окружность
yОкружность – множество точек плоскости
равноудаленных от данной точки плоскости,
называемой центром окружности.
С(x0; y0) – центр окружности,
R – радиус,
М(x; y) – произвольная точка окружности.
M
y0
C R
0
x0
x
CM R ( x x0 ) 2 ( y y0 ) 2
( x x0 ) 2 ( y y0 ) 2 R 2
Если центр окружности совпадает с началом координат,
уравнение примет вид
2
2
x y R2.
10
11.
Эллипсy
b
0
-a
с
-с
x
a
-b
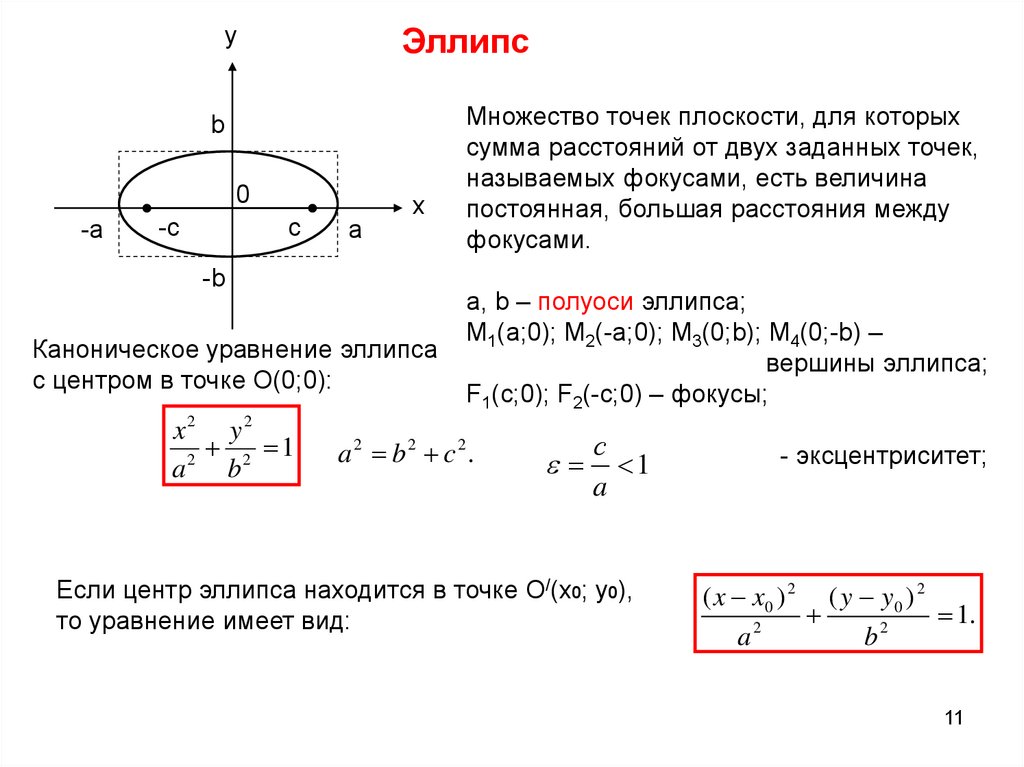
Каноническое уравнение эллипса
с центром в точке О(0;0):
x2 y2
1
a 2 b2
Множество точек плоскости, для которых
сумма расстояний от двух заданных точек,
называемых фокусами, есть величина
постоянная, большая расстояния между
фокусами.
а, b – полуоси эллипса;
М1(а;0); М2(-а;0); М3(0;b); М4(0;-b) –
вершины эллипса;
F1(c;0); F2(-c;0) – фокусы;
a2 b2 c2.
с
1
a
Если центр эллипса находится в точке О/(x0; y0),
то уравнение имеет вид:
- эксцентриситет;
( x x0 ) 2 ( y y 0 ) 2
1.
2
2
a
b
11
12.
Гиперболаy
b
y x
a
y
b
x
a
b
a
0
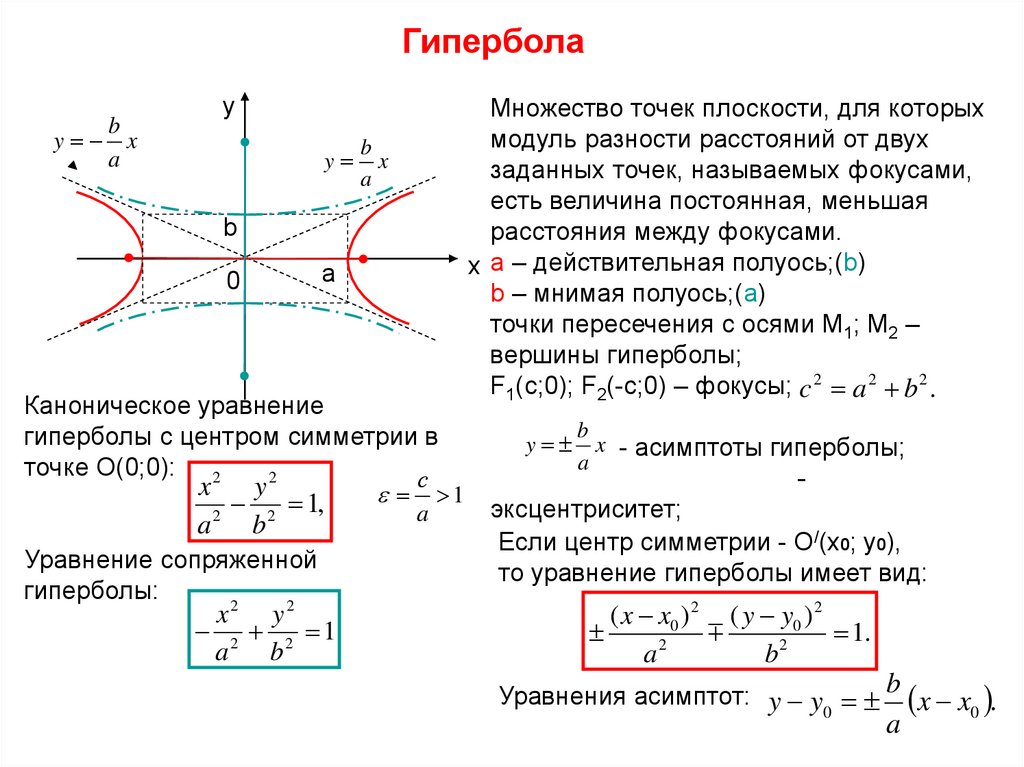
Каноническое уравнение
гиперболы с центром симметрии в
точке О(0;0): 2
с
x
y2
1
1,
a2
b2
Уравнение сопряженной
гиперболы:
x2 y2
2 2 1
a
b
a
Множество точек плоскости, для которых
модуль разности расстояний от двух
заданных точек, называемых фокусами,
есть величина постоянная, меньшая
расстояния между фокусами.
x а – действительная полуось;(b)
b – мнимая полуось;(a)
точки пересечения с осями М1; М2 –
вершины гиперболы;
F1(c;0); F2(-c;0) – фокусы; c 2 a 2 b 2 .
y
b
x - асимптоты гиперболы;
a
-
эксцентриситет;
Если центр симметрии - О/(x0; y0),
то уравнение гиперболы имеет вид:
( x x0 ) 2 ( y y0 ) 2
1.
2
2
a
b
Уравнения асимптот: y y0 b x x0 .
a
13.
ПараболаМножество точек плоскости, каждая из
которых находится на одинаковом
расстоянии от заданной точки, называемой
фокусом и прямой, называемой
директрисой.
y
p – параметр;
О(0;0) – вершина;
-p/2
0
p/2
x
F(p/2;0) – фокус;
y
p - уравнение директрисы.
2
Уравнение параболы:
y 2 2 px
13
14.
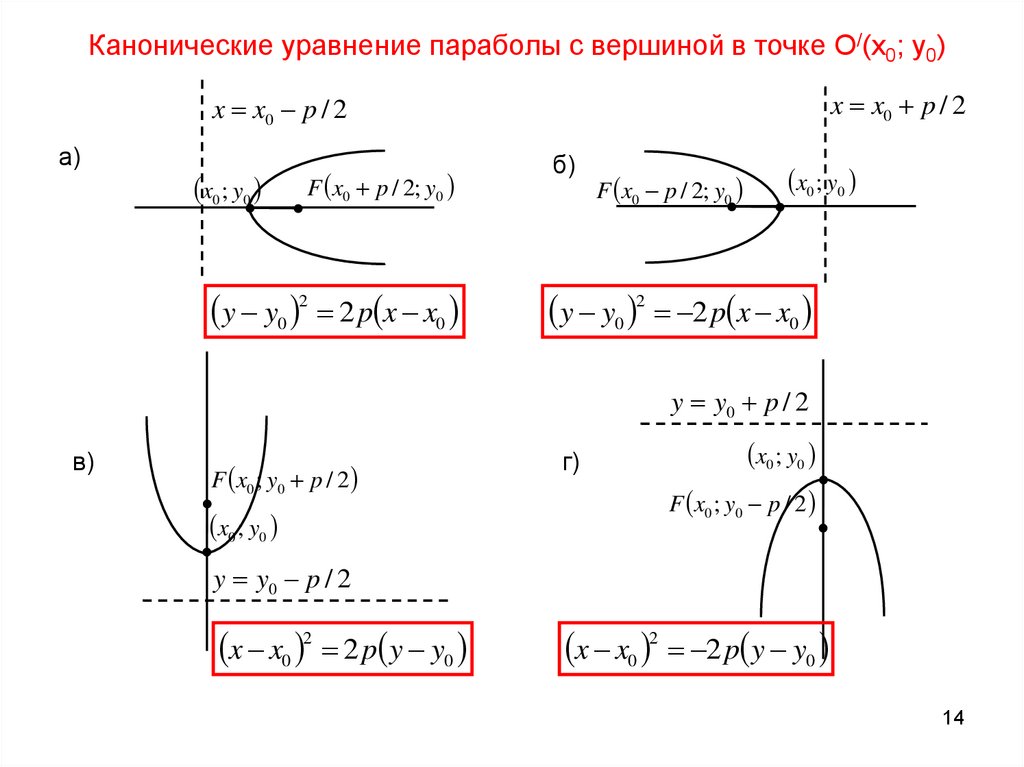
Канонические уравнение параболы с вершиной в точке О/(x0; y0)x x0 p / 2
x x0 p / 2
а)
x0 ; y0
F x0 p / 2; y0
y y0 2 2 p x x0
б)
F x0 p / 2; y0
x0 ; y0
y y0 2 2 p x x0
y y0 p / 2
в)
F x0 ; y0 p / 2
x0 ; y0
г)
x0 ; y0
F x0 ; y0 p / 2
y y0 p / 2
x x0 2 2 p y y0
x x0 2 2 p y y0
14
15.
Если уравнение кривой второго порядка записано в видеAx2 By 2 Cx Dy E 0
,
то при
A=B
кривая является окружностью;
А∙B>0
кривая является эллипсом;
А∙B<0
кривая является гиперболой;
А=0 и B≠0
кривая является параболой;
А≠0 и B=0
кривая является параболой.
15
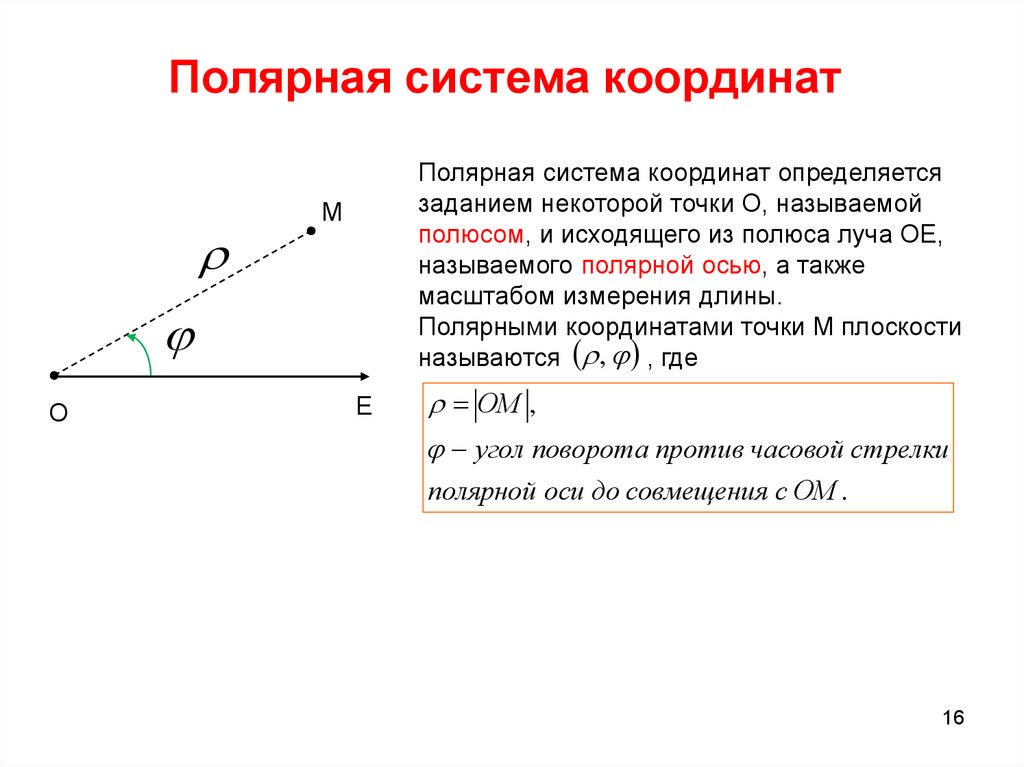
16. Полярная система координат
Полярная система координат определяетсязаданием некоторой точки О, называемой
полюсом, и исходящего из полюса луча ОЕ,
называемого полярной осью, а также
масштабом измерения длины.
Полярными координатами точки M плоскости
называются , , где
M
О
Е
ОМ ,
угол поворота против часовой стрелки
полярной оси до совмещения с ОМ .
16
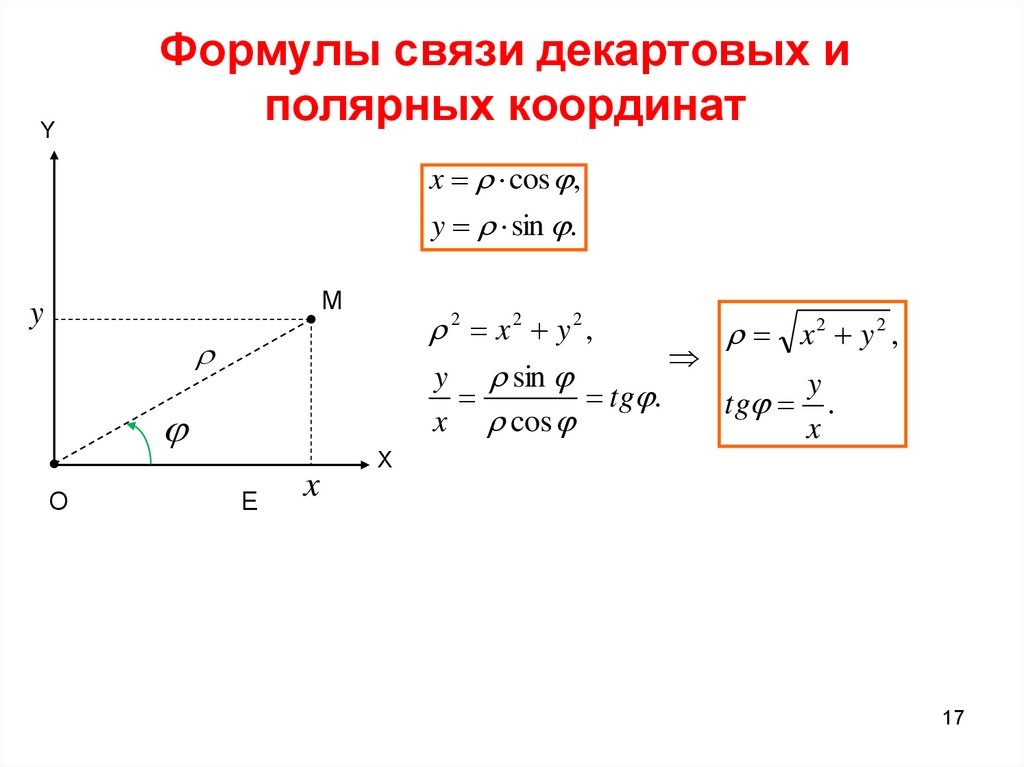
17. Формулы связи декартовых и полярных координат
YФормулы связи декартовых и
полярных координат
x cos ,
y sin .
M
y
2 x2 y2 ,
x2 y2 ,
y sin
y
tg .
tg .
x cos
x
О
Е
x
Х
17
18.
Задача. Кривая задана уравнением 2 cosв полярной системе координат. Построить кривую в
декартовой системе координат.
x2 y2 ;
x cos cos
x;
2 cos x 2 y 2 2
x
x2 y2
x2 y2 2x
x 2 y 2 2 x 0;
A B 1 имеем урвнение окружности, приведем уравнение
к каноническому виду и выполним построение.
18
19.
x 2 y 2 2 x 0 x x0 y y0 R 22
x
x
2
2x y 2 0
2
2x 1 y2 1
x 1 y 0
2
2
2
12
y
центр окружности 1;0
R=1
R 1
0
1
x
19













 mathematics
mathematics








