Показательные уравнения: типы и методы решения

1.

у=ах , a > 0, a 1, x R
Показательные
уравнения:
типы и методы
решения.
У
У
у=ах
0<a<1
1
1
0
a>1
Х
0
Х

2.

Концентрация
внимания
Выпишите в каждом ряду
лишнее (по смыслу
составления ряда) число
3
19
9
27
кратные 3
15
20
21
25
кратные 5
1
3
5
10
простые
5
12
22
56
чётные
11
37
24
51
нечётные
7
84
3
5
однозначны 19; 21; 10; 5; 24; 84; 9; 224.
е
24
35
78
9
двузначные
144
квадраты
121
169 224
Верным должен быть
следующий ряд чисел:
Концентрация внимания равна N.
N = (число верно указанных чисел) x 0,125 x 100%

3.

Пусть a>0, a≠1, b R
ax=b
– простейшее показательное уравнение
Пример:
x
1
2 8, 81, 5 x 3 7 , 6 x 10
3
x

4.

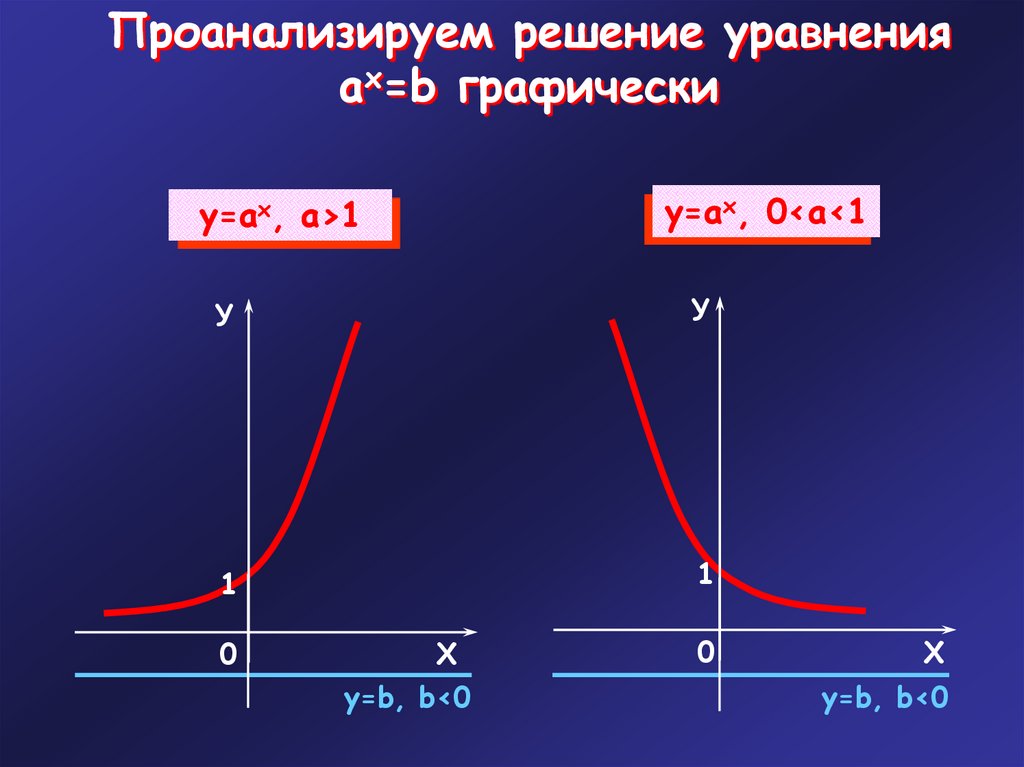
Проанализируем решение уравнения
ax=b графически
у=ах, 0<a<1
у=ах, a>1
У
У
1
1
0
Х
у=b, b<0
0
Х
у=b, b<0

5.

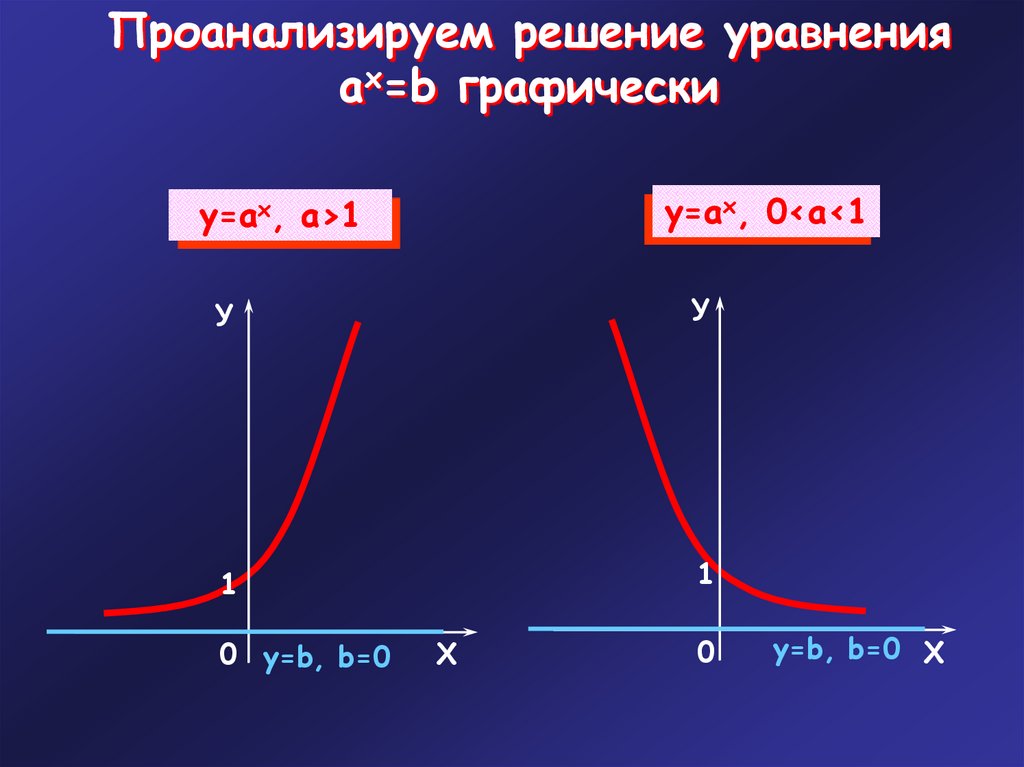
Проанализируем решение уравнения
ax=b графически
у=ах, 0<a<1
у=ах, a>1
У
У
1
1
0 у=b, b=0
Х
0
у=b, b=0 Х

6.

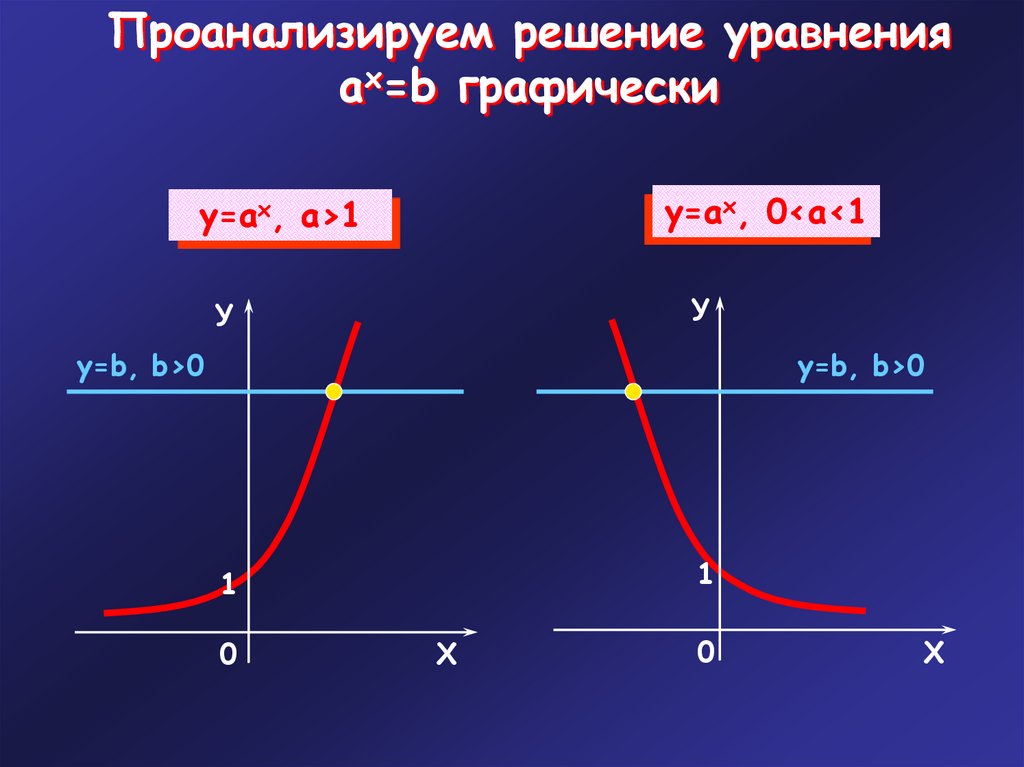
Проанализируем решение уравнения
ax=b графически
у=ах, 0<a<1
у=ах, a>1
У
У
у=b, b>0
у=b, b>0
1
1
0
Х
0
Х

7.

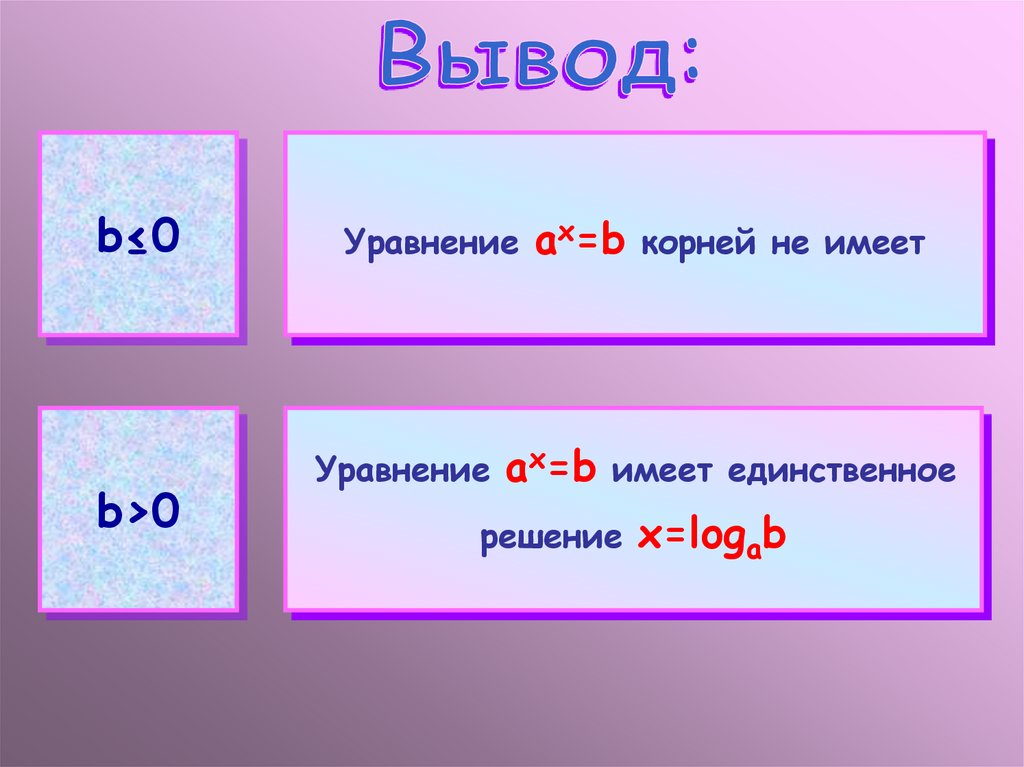
b≤0
b>0
Уравнение
Уравнение
ax=b
ax=b
корней не имеет
имеет единственное
решение
x=logab

8.

Пример:
1) 2 x 8,
x log 2 8,
8 0, уравнение имеет
единственное решение
x 3.
2) 3 х 5,
x log 3 5.
3) 5 25,
x
5 0, уравнение имеет
единственное решение
25 0, уравнение корней
не имеет.

9.

Замечание:
Во многих случаях решение показательных уравнений после
надлежащих преобразований сводится к решению простейших
показательных уравнений.
При решении показательных уравнений часто используется
следующая теорема:
«Уравнение
уравнению
a f(x) a g(x) , a 0 и a 1
f(x) g(x) ».
равносильно
В общем, виде справедлива теорема
a f(x) a g(x)
f(x) g(x) a 0 , a 1,
a 1.
«Уравнение
равносильно совокупности
».

10.

ТИП
ПРИМЕР
Решение
Простейшие показательные
уравнения.
9
9
x 2 4x 4,5
x 2 4x 4,5
3
2
3
3,
х 2 4х 4,5
3,
2(х 2 4х 4,5)
3
3,
2 х 2 4х 4,5 1,
х 2 4х 4,5 0,5,
2
х 4х 5 0,
х 5,
х 1.
ОТВЕТ:
-5 ; 1.

11.

ТИП
Показательные уравнения, сводящиеся к
уравнениям относительно функции
одного аргумента.
ПРИМЕР
212х 1 46х 1 84х 1 16 3х 1 1280
Решение
2 12х 1 4 6х 1 8 4х 1 16 3х 1 1280,
2 12х 1 (2 2 ) 6х 1 23 4х 1 24 3х 1 1280,
2 12х 1 2 12х 2 2 12х 3 2 12х 4 1280,
2 12х 4 23 22 2 1 1280,
2 12х 4 5 1280,
2 12х 4 256,
12х 4
8
2
2 ,
12х 4 8,
12х 12,
ОТВЕТ:
х 1.
1.

12.

ТИП
ПРИМЕР
Решение
Показательные уравнения,
сводящиеся к квадратным
уравнениям.
9
9
3
3
х 2 1
х 2 1
36 3
36 3
2(х 2 1)
2(х 2 1)
х2 3
х2 3
36 3
3 0
3 0,
х 2 1 2
2
36 3 3
3 4 3
х 2 1 2
Пусть t 3
х 2 1
x 2 1
t 2 4t 3 0,
3 0,
х 2 1
3 0,
3 0,
, t 0, тогда

13.

ТИП
Показательные уравнения,
сводящиеся к квадратным
уравнениям.
ПРИМЕР
t 3,
t 1,
t 0;
9
36 3
t 3,
t 3,
t
0,
t 1, t 1.
t 0;
Вернемся
к переменной Х
ОТВЕТ:
х 2 1
х2 3
3 0
.
3 x 1 3, x 2 1 1, x 2 2, x 2 ,
2
2
2
x 1
3
1; x 1 0; x 1; x 1.
2
x 2 ,
x 1.

14.

ТИП
Однородные показательные
уравнения первой и второй степени.
ПРИМЕР 1
2
Решение
2
2
3
х 2 1
3 3
х 2 1
х2 2
2
2
х 2 1
х 2 1
х 2 1
х2
2
х2
х 2 1
3
3
2
х 2 1
х 2 1
х2 2
2
х2 2
,
3 ,
х2
1 2 3 3 1 ,
3
9 3
х 2 1
х 2 1
4; 3
x 2 1
9 0, при х R

15.

ТИП
Однородные показательные
уравнения первой и второй степени.
ПРИМЕР 1
Решение
2
2
3
х 2 1
х 2 1
9
9
х 2 1
3
3
х 2 1
х 2 1
х 2 1
4
9
4
2
,
9
3 2
х 1
2
2
2
,
3
3
х 2 1 2,
х 2 3,
х 3.
ОТВЕТ:
х 3
3
,
х2
3
х 2 1
2
х2 2

16.

ТИП
Однородные показательные
уравнения первой и второй степени.
ПРИМЕР 2
3 4 2 9 5 6
х
х
х
Решение
3 4х 2 9х 5 6х ,
3 2 2 3 5 2 3 0,
2х
2х
х
3 2 2х 5 2 х 3х 2 32х
2x
0
;
3
0, при x R
2х
2х
2х
3
3
3

17.

ТИП
Однородные показательные
уравнения первой и второй степени.
ПРИМЕР 2
Решение
3 4х 2 9х 5 6х
2х
х
2
2
3 5 2 0.
3
3
3t 2 5t 2 0,
2
2 t 3 ,
2
t 3 ,
t ,
t
0,
3
t 1,
t 1.
t
1,
t 0;
t 0;
ОТВЕТ:
0;1
х
2
Пусть t , t 0, тогда
3
Вернёмся
к переменной x
2
2
,
3
3
x
2 1;
3
.
x
x 1,
x 0.

18.

ТИП
Показательные уравнения,
сводящиеся к рациональным
уравнениям.
ПРИМЕР 1
Решение
t 1,
t 5,
t 0;
5 х 51 х 6 0
5х 51 х 6 0,
5
х
х
Пусть
5
t , t 0, тогда
5 х 6 0.
5
5
t 6 0,
t
Вернёмся
t 2 6t 5 0,
t 1,
t 0,
t 5,
t 0;
к переменной x
t 1,
t 5.
5 x 1, x 0,
x
x 1.
5 5;
ОТВЕТ:
0 ; 1.

19.

ТИП
Показательные уравнения,
сводящиеся к рациональным
уравнениям.
1
5
ПРИМЕР 2
2 х
х
0.
3 1 3 3
Решение
1
5
х
2
0.
3 1 3 3
1
5
2
0,
t 1 t 3
х
х
Пусть 3 t , t 0, тогда
2 t 1 t 3 t 3 5 t 1
0,
t 1 t 3
t2 t 2
0,
t 1 t 3
t 1 t 2 0,
t 1 t 3
t 1 t 2 0,
t 1 t 3 0;
t 1,
t 2,
t 1 , t 3;
t 1,
t 2.

20.

ТИП
Показательные уравнения,
сводящиеся к рациональным
уравнениям.
1
5
ПРИМЕР 2
2 х
х
0.
3 1 3 3
Решение
t 1,
t 1,
t 0,
Т.к. t 0, то t 2,
t 2,
t 0;
t 0;
Вернёмся к переменной x
3x 2,
x log 3 2.
ОТВЕТ:
log 3 2
t 2.

21.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 1
2х 5х 7 х
Решение
2х 5х 7 х ,
х
х
х
2
5
7
х
х х , 7 0, при х R
х
7
7
7
х
х
2 5
1.
7 7

22.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 1
Решение
2 5 7
х
х
х
x
x
Введём функции f(x) 2 5 и g(x) 1 .
7 7
x
x
2
5
Функция f(x) убывает на R, как сумма
7 7
убывающих на R. Функция g(x) 1 постоянна на R.
Горизонтальная прямая g(x) 1 может пересечь график
x
x
2
5
функции f(x) не более чем в одной точке.
7 7
Следовательно, уравнение
2 х 5 х 7 х имеет не более
одного корня. Корнем уравнения является x=1.
Проверим это.
ОТВЕТ:
1
2 5
1, 1 1.
7 7

23.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 2
3
Решение
3х 2
х 2
9
х
9
.
х
Легко определить и проверить,
что х=3 - корень данного уравнения.
х 3,
3
3 2
9
,
3
3 3.
Покажем, что других корней уравнение
иметь не может.

24.

ТИП
ПРИМЕР 2
Решение
Показательные нестандартные
уравнения.
3
х 2
9
х
Справедливы следующие утверждения:
Если функция f(x) возрастает (убывает)
на множестве I, то уравнение
f(x) b
не может иметь на I более одного корня.
Если функция f(x)возрастает на I, а функция
g(x) убывает на I, то уравнение
f(x) g(x)
не может иметь на I более одного корня.

25.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 2
Решение
3
х 2
9
х
Введём функции f(x) 3 х 2 и g(x)
9
.
х
Показательная функция f(x) 3 х 2 ( а 3 , 3 1 , a 1 )
возрастает на R.
Функция g(x) 9 (обратная пропорциональность)
х
убывает на каждом из промежутков ;0 , 0; .
Таким образом, на ;0 и на 0; уравнение имеет
не более одного корня, т. е. х 3 - единственный корень
данного уравнения.
ОТВЕТ:
3

26.

ТИП
ПРИМЕР 3
Решение
Показательные нестандартные
уравнения.
х 3
х2 х
х 3
7х 5
Прежде всего, заметим, что функция y f(x) g(x)
не является показательной функцией.
Существуют две точки зрения, оценивающие область
определения данной функции.
f(x) 0
a) f(x) 0;
f(x) 0, если g(x) Z,
b)
f(x) 0, если g(x) 0.

27.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 3
Решение
х 3
х2 х
х 3
7х 5
Решим данное уравнение, придерживаясь второй
точки зрения.
Вначале проверим, какие из решений совокупности
х 3 0,
х 3 1,
х 3 1;
х 3,
х 2,
х 4;
являются корнями данного уравнения.
Проверка.
х 2
2 3 4 2 2 3 14 5 ,
1 6 1 9 ,
1 1.
Проверка показала, что x=2 не является корнем уравнения.

28.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 3
Решение
х 3
х2 х
х 3
7х 5
3 3 9 3 3 3 21 5 ,
х 3
012 016 ,
0 0.
Проверка показала, что x=3 является корнем
уравнения.
х 4
4 3 16 4 4 3 28 5 ,
120 123 ,
1 1.
Проверка показала, что x=4 является корнем
уравнения.

29.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 3
Решение
х 3
х2 х
х 3
7х 5
Теперь установим, какие из корней уравнения
х 2 х 7х 5 удовлетворяют исходному уравнению.
х 2 х 7х 5,
х 2 6х 5 0,
х 5,
х 1.
Проверка.
х 1
1 3 1 1 1 3 7 5
2 2 2 2 .
Проверка показала, что x=1 является корнем уравнения.

30.

ТИП
Показательные нестандартные
уравнения.
ПРИМЕР 3
Решение
х 3
х2 х
х 3
7х 5
х 5
5 3
25 5
5 3
35 5
,
2 2 .
30
30
Проверка показала, что х=5 является корнем
уравнения.
Замечание: если придерживаться первой точки
зрения, то корни х=1 и х=3 следует исключить.
ОТВЕТ:
5;4;3;1

31.

32.

Выполнил:
Бобров Р.С.