Решение комбинаторных задач

1.

РЕШЕНИЕ
КОМБИНАТОРНЫХ
ЗАДАЧ
Решение комбинаторных задач
1

2.

ПЕРЕСТАНОВКА
Задача 1
На полке стоят три книги. Сколькими способами
можно расставить эти книги на полке?
abc, acb
bac, bca
cab, cba
Pn = n!
Решение комбинаторных задач
2

3.

РАЗМЕЩЕНИЕ
Задача 2
Из 12 учащихся нужно отобрать по одному человеку для участия в
городских олимпиадах по математике, физике, истории
и
географии. Каждый из учащихся участвует только в одной
олимпиаде. Сколькими способами это можно сделать?
11880
Решение комбинаторных задач
3

4.

СОЧЕТАНИЕ
Задача 3
Из вазы с цветами, в которой стоят 10 красных роз и 5
белых , выбирают 2 красные розы и 1 белую. Сколькими
способами можно сделать такой выбор букета?
Решение
- выбор двух красных роз из 10
- выбор белой розы
225
Решение комбинаторных задач
4

5.

СОЧЕТАНИЕ
Решение комбинаторных задач
5

6.

ПЕРЕСТАНОВКИ, РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
Решение комбинаторных задач
6

7.

КОМБИНАТОРНЫЕ ЗАДАЧИ
• Правило суммы:
Если объект А выбран - m
способами, а объект В – n способами, то выбор «либо А,
либо В» - m+n способами.
• Правило произведения: Если объект А выбран
m способами, а после каждого из таких выборов объект
В выбран n – способами, то выбор «А и В» в указанном
порядке m*n
Решение комбинаторных задач
7

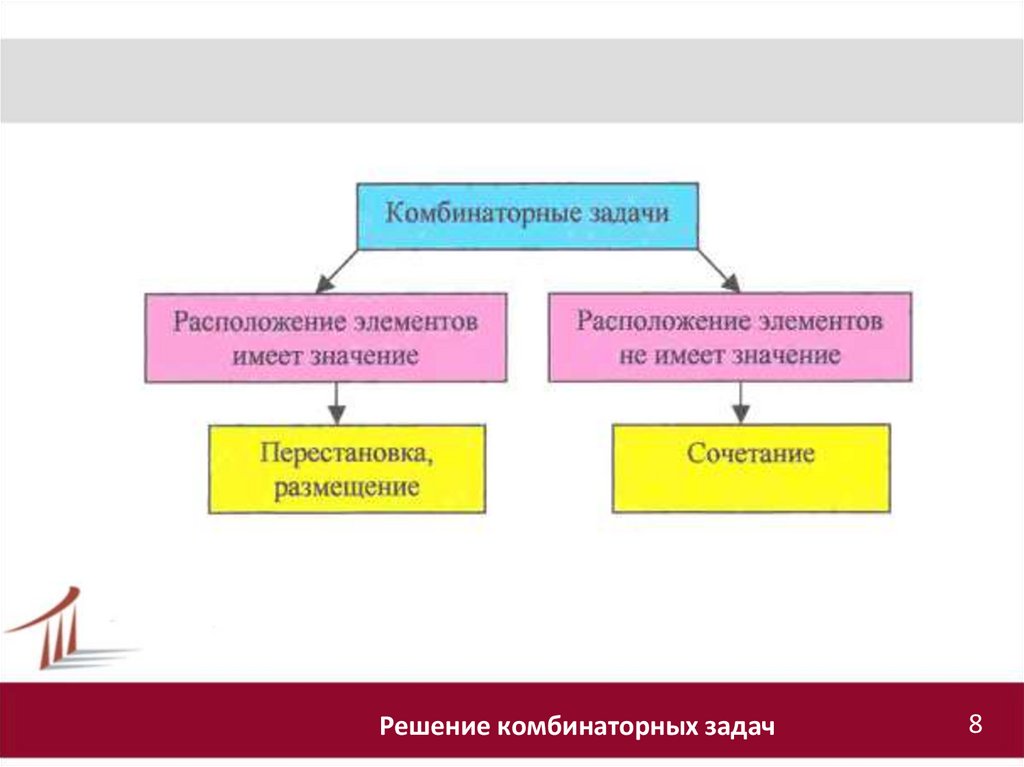
8.

Решение комбинаторных задач
8

9.

ЗАДАЧА 1
Сколько существует трехзначных
чисел, составленных из цифр 1,2,3,4,5,6
(без повторений), которые не кратны 3?
Решение комбинаторных задач
9

10.

РЕШЕНИЕ
1,2,3 1,3,5 2,3,4
Числа кратные 3: 1,2,6 1,5,6 2,4,6
Составим Р3 чисел , кратных 3
Всего троек 8
Всего трехзначных чисел кратных 3
3,4,5
4,5,6
Количество трехзначных чисел не кратных трем
Решение комбинаторных задач
10

11.

ЗАДАЧА 2
Из
спортсменов
А,Б,В,Г,Д
и
Е
выбирается пара для участия в
соревнованиях пар по теннису. Сколько
существует способов выбора этой пары?
Решение комбинаторных задач
11

12.

РЕШЕНИЕ
Каждая пара должна отличаться хотя
бы одним из учащихся. Таких групп
должно быть
Решение комбинаторных задач
12

13.

ЗАДАЧА 3
На плоскости отмечены 10 точек,
причем никакие 3 из них не лежат в
одной плоскости. Через каждые 2 из них
проведена прямая. Сколько проведено
прямых.
Решение комбинаторных задач
13

14.

РЕШЕНИЕ
Сочетание
Количество прямых равно
Решение комбинаторных задач
14

15.

ЗАДАЧА 4
Сколько
человек
участвовало
в
шахматном турнире, если известно, что
каждый участник сыграл с каждым из
остальных по одной партии, и всего было
сыграно 136 партий?
Решение комбинаторных задач
15

16.

РЕШЕНИЕ
n - количество участников
- количество сыгранных партий
Решение комбинаторных задач
16

17.

РЕШИТЬ УРАВНЕНИЕ
Решение
Решение комбинаторных задач
17

18.

РЕШИТЬ УРАВНЕНИЕ
Решение
Решение комбинаторных задач
18

19.

РЕШИТЬ УРАВНЕНИЕ
Решение
Решение комбинаторных задач
19

20.

РЕШИТЬ УРАВНЕНИЕ
Решение
Решение комбинаторных задач
20

21.

ДОКАЗАТЬ
ТОЖДЕСТВО
Решение
Решение комбинаторных задач
21

22.

РЕШИТЕ НЕРАВЕНСТВО
Решение
Решение комбинаторных задач
22

23.

СПАСИБО
ЗА ВНИМАНИЕ !!!
Решение комбинаторных задач
23