Матрица смежности

1.

Сколько существует различных путей из
города А в город D?
Задание 1
Таблицу заполнили.
Такую таблицу называют Матрица смежности
A
Заполним таблицу
признаками наличия дорог.
При наличии дороги между
пунктами на пересечении
соответствующей строки и
колонки поставим «+»
A
B
C
D
E
F
G
H
B
+
C
D
+
E
+
F
G
+
H
+
+
+
+
+
+
+
+
+
+

2.

Сколько существует различных путей из
города А в город D?
Задание 1
Второй этап.
Определение количества путей.
Построчно будем заполнять
диагональные серые клетки
(это вершины графа)
количеством ведущих туда
путей.
Примем, что в пункт А
ведет один путь.
Не важно как, но мы туда
каким-то путём попали?
Запишем, что в А ведет
единственная дорога.
A
B
C
D
E
F
G
H
A
1
B
+
C
D
+
E
+
+
F
G
+
H
+
+
+
+
+
+
+
+
+

3.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
1. Для узла В
В узел В ведёт единственная
дорога из узла А. Копируем из А
значение «1» (то есть
количество дорог, ведущих в А).
Это значит, что в В попасть
можно тоже единственным
путём через А.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
E
+
+
F
G
+
H
+
+
+
+
+
+
+
+
+

4.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
2. Для узла G
В узел G тоже ведёт
единственная дорога из узла А.
В колонке G крестик стоит
только в строке А. Это значит,
что в G попасть можно
единственным путём через
узел А.
Копируем из А значение «1».
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
E
+
+
F
G
+
H
+
+
+
+
+
+
+
1
+
+

5.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
3. Для узла С
Мы не можем определить
количество путей в узел С, так
как неизвестно количество
путей в узел Е.
Определим эту величину для Е.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
E
+
+
F
G
+
H
+
+
?
+
+
+
+
+
1
+
+

6.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
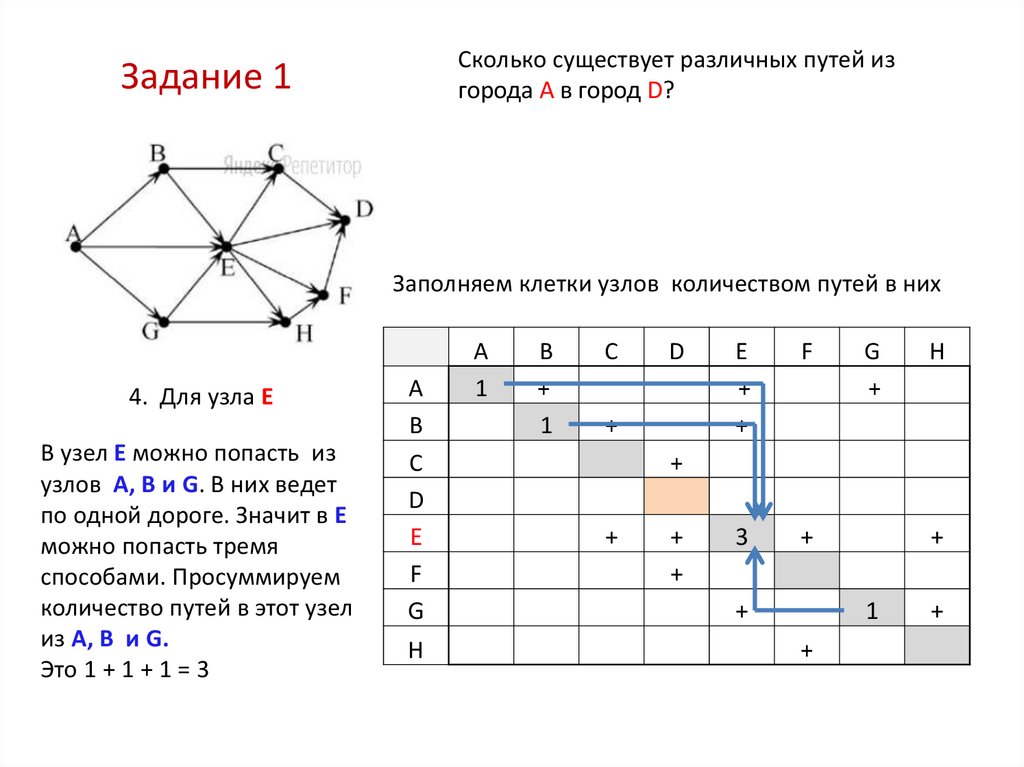
4. Для узла E
В узел Е можно попасть из
узлов А, В и G. В них ведет
по одной дороге. Значит в Е
можно попасть тремя
способами. Просуммируем
количество путей в этот узел
из А, В и G.
Это 1 + 1 + 1 = 3
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
E
+
+
F
3
+
G
+
H
+
+
+
+
+
+
1
+
+

7.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
5. Для узла С
В колонке С видим, что
крестики стоят в строках В и Е.
Значит в С можно попасть
двумя способами: из Е и из В.
Суммирует количество путей,
которыми можно попасть в
эти пункты.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
4
+
+
+
+
E
+
+
F
3
+
+
G
+
+
1
+
H
+

8.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
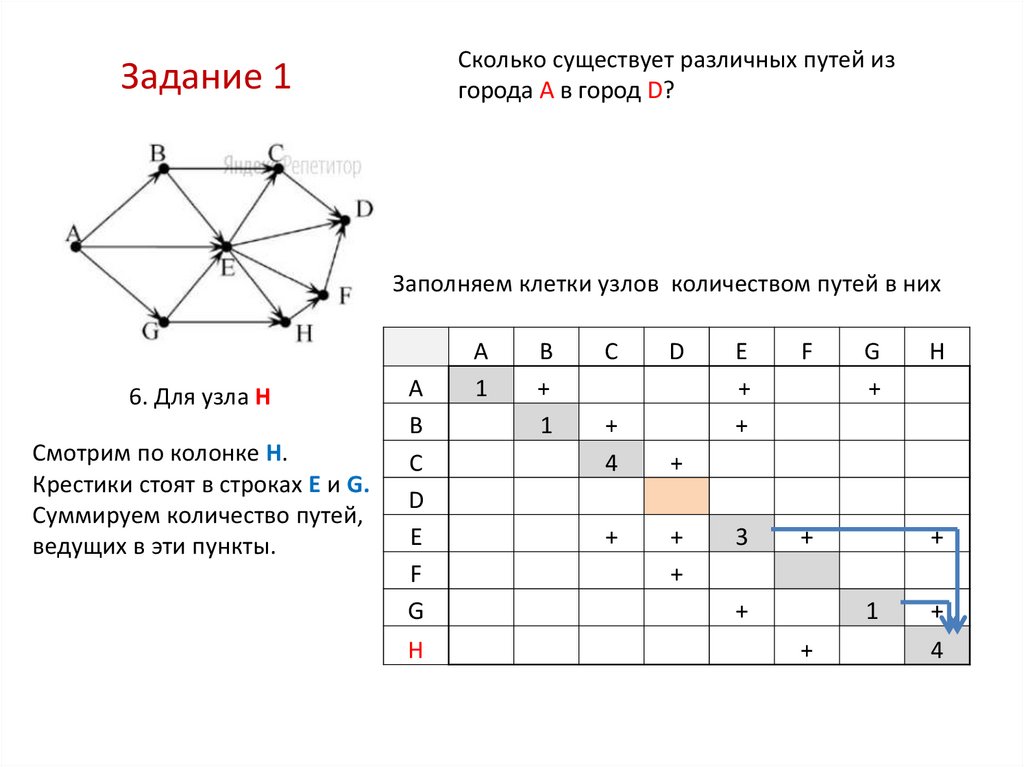
6. Для узла H
Смотрим по колонке Н.
Крестики стоят в строках Е и G.
Суммируем количество путей,
ведущих в эти пункты.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
4
+
+
+
+
E
+
+
F
3
+
+
G
+
+
1
+
H
+
4

9.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
7. Для узла F
Попасть в F можно только
из H и Е. Заполним
диагональную клетку F
суммой путей в узлы H и Е.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
D
+
4
+
+
+
+
E
+
+
F
3
+
7
+
G
+
+
1
+
H
+
4

10.

Сколько существует различных путей из
города А в город D?
Задание 1
Заполняем клетки узлов количеством путей в них
8. Для узла D
В пункт D можно попасть:
из С (куда ведут 4 пути),
из F (куда ведут 7 путей),
и из Е (куда ведут 3 пути).
Итого:
из А в D ведёт 14 путей.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
+
4
+
D
+
14
+
+
E
+
+
F
3
+
7
+
G
+
+
1
+
H
+
4

11.

Сколько существует различных путей из
города А в город D?
Задание 1
Из А в D ведёт 14 путей.
A
B
C
D
E
F
G
H
A
1
B
+
1
C
+
4
+
D
+
14
+
+
E
+
+
F
3
+
7
+
G
+
+
1
+
H
+
4

12.

Задание 1а
Сколько существует различных путей из города А в город D?
Второе решение: преобразуем граф во взвешенный, отмечая
количество путей в каждый узел.

13.

Сколько существует различных путей из города А в город D?
Второе решение: преобразуем граф во взвешенный, отмечая
количество путей в каждый узел.
Задание 1а
4
1
14
3
1
7
1
4

14.

Задание 2
Сколько существует различных путей из
города А в город К.
.
Отметим крестиками (+)
существующие дороги
А
Б
В
Г
Д
Е
Ж
К
А
1
Б
В
Г
Д
Е
Ж
К

15.

Задание 2
Сколько существует различных путей из
города А в город К.
.
Отметим крестиками (+)
существующие дороги
Построчно будем заполнять
диагональные клетки
количеством ведущих туда
дорог.
А
Б
В
Г
Д
Е
Ж
К
А
1
Б
+
1
В
+
+
2
Г
+
Д
+
Е
Ж
+
+
2
+
1
К
+
+
+
3
1
+
+
8

16.

Задание 2
Сколько существует различных путей из
города А в город К.
.
А
Б
В
Г
Д
Е
Ж
К
А
1
Б
+
1
В
+
+
2
Г
+
Д
+
Е
Ж
+
+
2
+
1
К
+
+
+
3
1
+
+
8

17.

1
Задание 3
Какая из компаний
обеспечивает минимальную
стоимость перевозок из А в В?
A
B
C
D
E
А
B
3
1
1
4
A
B
C
D
E
3
1
B
D
1
E
1
2
2
2
А
C
3
4
3
C
3
4
4
2 2
D
1
E
2
2
А
A
B
C
D
E
B
3 4
1
4 2
C
3
4
2
D
1
E
4
2
2

18.

А
1
A
B
C
D
E
3
1
1
B
7
4
C
3
4
D
1
Какая из компаний
обеспечивает минимальную
стоимость перевозок из А в В?
E
1
2
3
С
4
2
B
7
Начнем с первой компании
А
1
D
1
E
2
2
C
E
4
B
7
2
E
Первая компания обеспечит минимальную стоимость перевозки равную 7

19.

А
2
A
B
C
D
E
3
1
B
7
4
C
3
4
D
1
Какая из компаний
обеспечивает минимальную
стоимость перевозок из А в В?
E
2
2
3
С
4
2 2
B
7
А
1
D
2
E
2
B
7
Что по второй компании?
Вторая компания обеспечит минимальную стоимость перевозки тоже равную 7

20.

А
3
A
B
C
D
E
B
6
3 4
1
4 2
C
3
4
D
1
Какая из компаний
обеспечивает минимальную
стоимость перевозок из А в В?
E
4
2
2
3
4
B
7
E
2
E
2
B
7
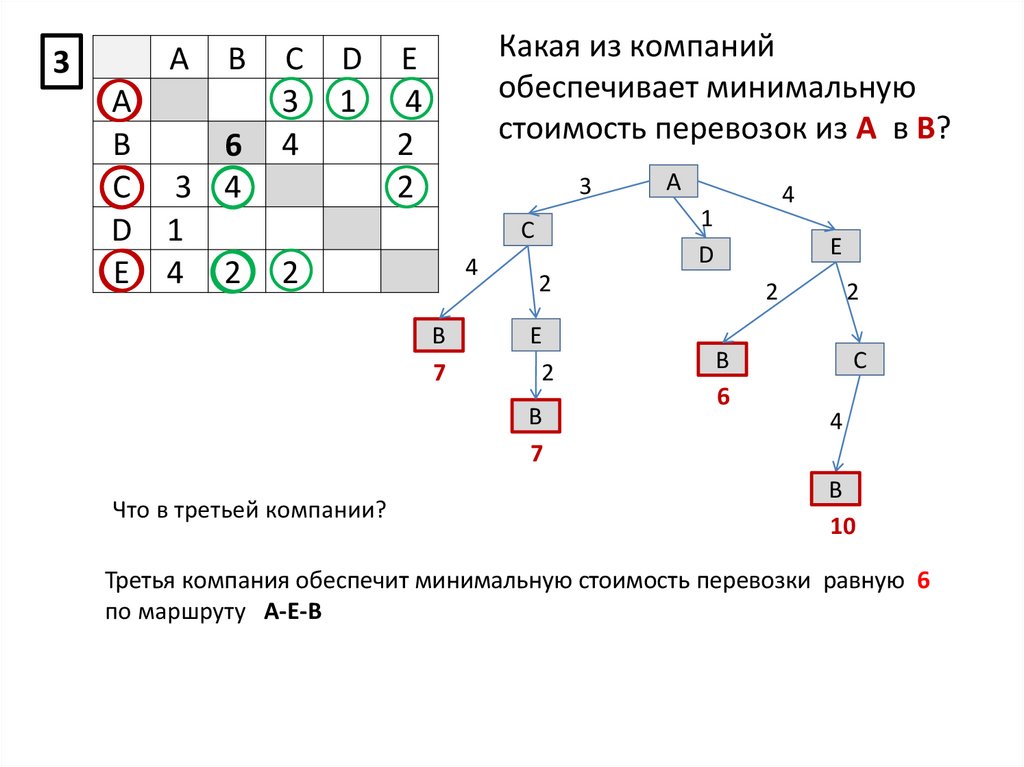
Что в третьей компании?
4
1
D
С
2
А
2
B
6
2
C
4
B
10
Третья компания обеспечит минимальную стоимость перевозки равную 6
по маршруту А-Е-В

21.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
B
3
C
5
1
1
D
F
15
4
4
6
Из пункта А в пункт F есть прямая
дорога протяженностью 15
Посмотрим другие пути, может они
короче?
2
2
15
E
1
6
1
15
?
Будем записывать в диагональные
серые клетки таблицы (вершины
графа) текущие найденные
кратчайшее расстояние до этих узлов.
Далее используем эти данные для
вычисления пути в другие узлы.

22.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
B
3
36
C
5
1
1
D
F
15
4
6
1
15
?
2
2
15
E
4
6
1
Из А в узел В можно попасть через С.
Длина пути будет 6 (0 + 5 + 1 = 6)
Однако видно, что через В путь
короче. Здесь длина пути будет 3.
(0 + 3 = 3)
Занесём найденное кратчайшее
расстояние. Заменим 6 на 3.

23.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
B
3
3
1
C
5
1
E
F
15
20
4
4
6
1
6
1
15
?
2
2
15
D
Будем в диагональные серые клетки
таблицы (вершины графа) записывать
кратчайшее расстояние до них.
Определим кратчайший путь из А
до узла С
В пункт С ведет три пути.
Из А (0 + 5 =5), из В (3 + 1 =4).
Это видно по длине пути в эти
пункты из узловых (серых) клеток
таблицы и длины пути из них до С.
Третий путь из D.
Оценим кратчайший путь в D из А,
минуя С.
Это через Е: 4 + 1 + 15 = 20
Или через F: 6 + 15 = 21
Проставим в узел D наименьшее
значение - число 20.

24.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
B
3
3
1
C
5
1
D
4
2
20
4
6
2
15
E
F
15
4
6
1
15
?
1
Вернемся к пункту С.
Туда ведет три пути:
Из А (0 + 5 = 5),
Из В (3 + 1 = 4) и
из D (20 + 2 = 22).
Проставим в узел С кратчайшее
расстояние через узел В, равное 4.

25.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
15
B
3
3
1
C
5
1
4
2
D
2
20
4
6
E
4
1
F
15
6
1
15
?
Скорректируем длину пути в узел D.
Видно, что из С в D кратчайший путь
длиной 4 + 2 = 6. Это меньше 20.

26.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
15
B
3
3
1
C
5
1
4
2
D
2
6
4
6
E
4
1
F
15
6
1
15
?
Скорректируем длину пути в узел D.
Видно, что из С в D кратчайший путь
длиной 4 + 2 = 6. Это меньше 20.
Заменим кратчайший путь до узла В
на меньшее значение.

27.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
15
B
3
3
1
C
5
1
4
2
D
2
6
4
6
E
F
15
Определим длину пути в узел Е.
В этот узел можно попасть из D и F.
Путь из D в Е длиной 10 (6 + 4 = 10)
4
10
1
6
1
15
?
Путь из F в Е длиной 16 (15 + 1 = 16)
Внесём меньшее значение.

28.

Определите длину кратчайшего пути между пунктами
A и F. Передвигаться можно только по дорогам,
протяжённость которых указана в таблице.
Задание 4
A
B
C
D
E
F
А
0
3
5
15
B
3
3
1
C
5
1
4
2
D
2
6
4
6
E
4
10
1
F
15
6
1
11
15
Выполняем последнее действие по
определению кратчайшего пути.
Видим, что путь через Е в F короче.
Он составляет 11 из Е
против 15 из А в пункт F
Заменим на меньшее значение.
Ответ: Кратчайший путь из A в F
равен 11.

29.

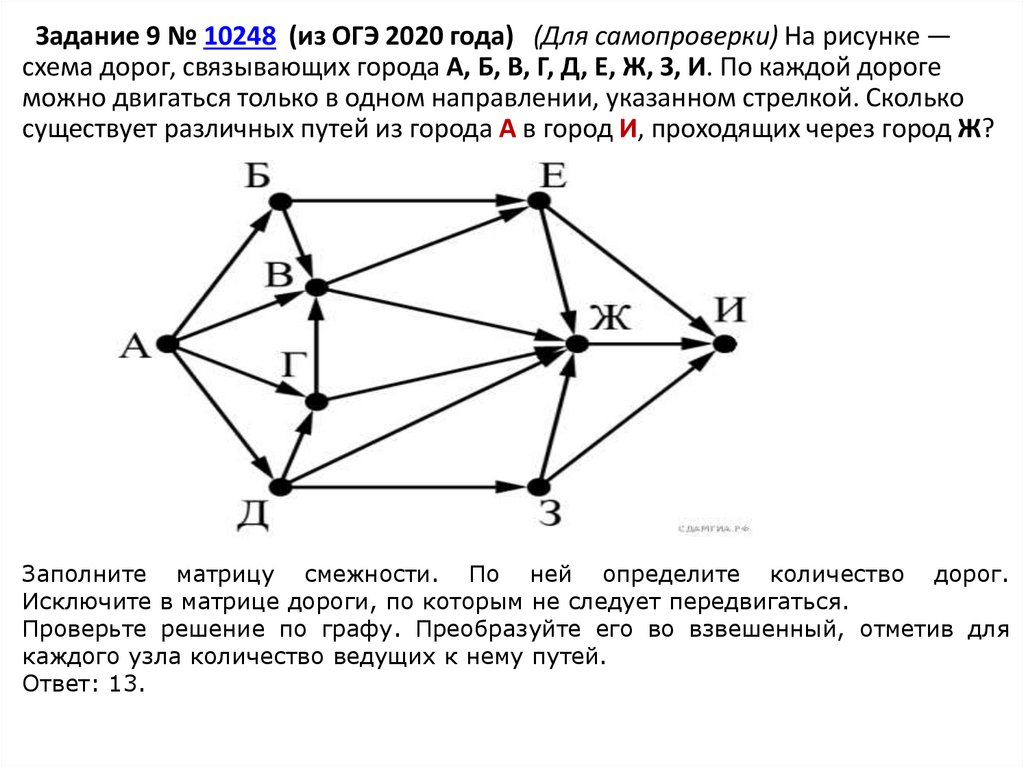
Задание 9 № 10248 (из ОГЭ 2020 года) (Для самопроверки) На рисунке —
схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге
можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город И, проходящих через город Ж?
Заполните матрицу смежности. По ней определите количество дорог.
Исключите в матрице дороги, по которым не следует передвигаться.
Проверьте решение по графу. Преобразуйте его во взвешенный, отметив для
каждого узла количество ведущих к нему путей.
Ответ: 13.

30.

Задание 4 № 63 (для самопроверки)
(из заданий ОГЭ на 2020 год)
Между населёнными пунктами А, В, С, D, Е построены дороги,
протяжённость которых (в километрах) приведена в таблице:
A
A
B
B
C
D
E
4
2
8
1
1
C
4
4
D
2
4
E
8
4
4
Определите длину кратчайшего пути между пунктами А и E.
Передвигаться можно только по дорогам, протяжённость которых
указана в таблице.
Ответ : 7.
Сверьте с полученным вами. Ещё можно проверить, нарисовав
по таблице граф и проставив там по узлам найденные
кратчайшие расстояния.

31.

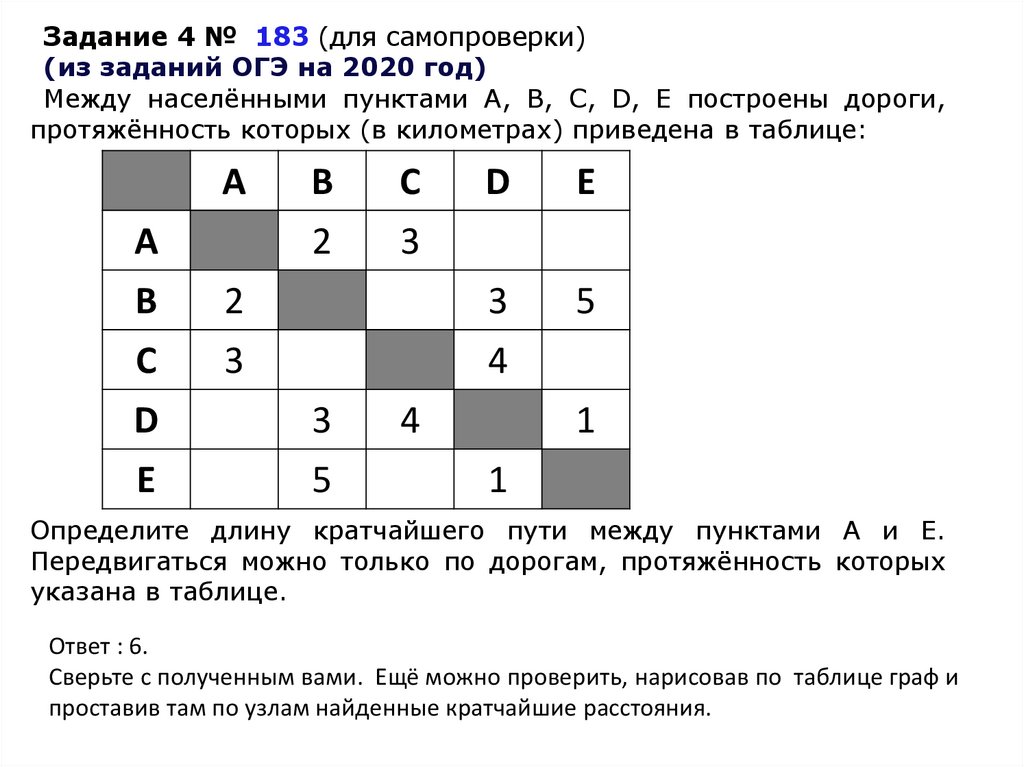
Задание 4 № 183 (для самопроверки)
(из заданий ОГЭ на 2020 год)
Между населёнными пунктами А, В, С, D, Е построены дороги,
протяжённость которых (в километрах) приведена в таблице:
A
A
B
C
D
E
B
2
C
3
2
3
3
5
D
E
3
4
5
4
1
1
Определите длину кратчайшего пути между пунктами А и E.
Передвигаться можно только по дорогам, протяжённость которых
указана в таблице.
Ответ : 6.
Сверьте с полученным вами. Ещё можно проверить, нарисовав по таблице граф и
проставив там по узлам найденные кратчайшие расстояния.