Представление и обработка информации в компьютере

1.

Представление и обработка
информации в компьютере

2.

Общие понятия кодирования
информации
Алфавит - конечный упорядоченный набор
знаков, используемых для передачи сообщений.
Слово - последовательность символов алфавита.
Код - правило отображения одного алфавита в
другой, а сама процедура - перекодировкой
сообщения (или системой кодирования).
Двоичный алфавит – {0, 1}.
Каждый символ двоичного алфавита называется
битом.
Последовательность из 0 и 1 называется
двоичным кодом.

3.

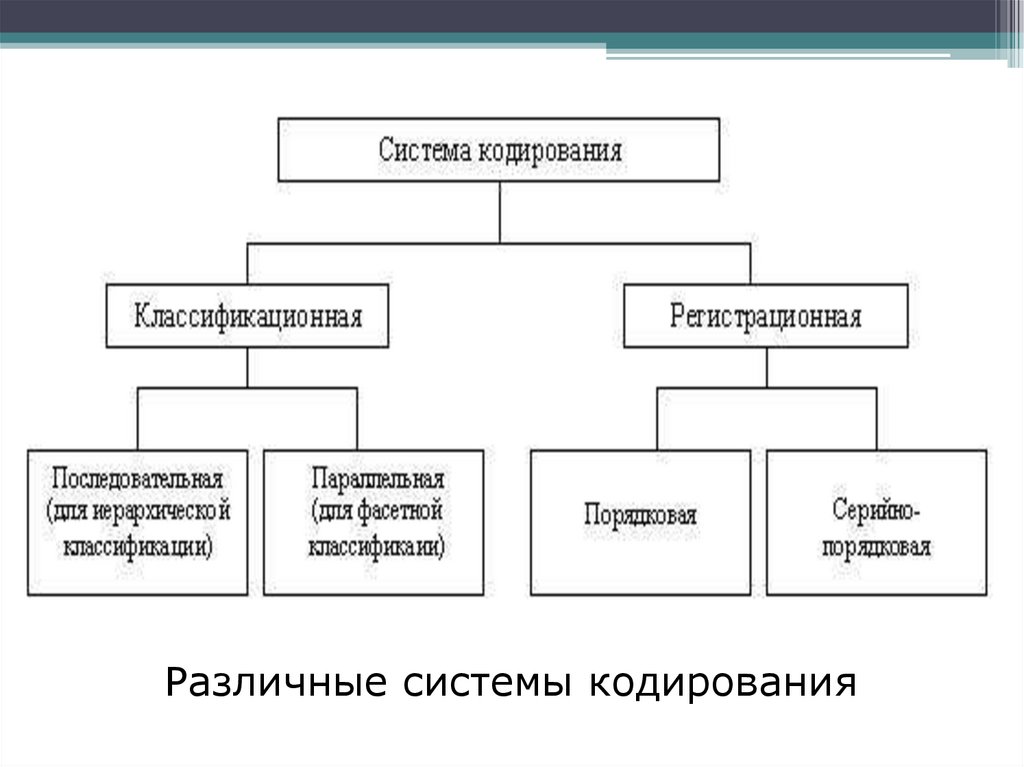
Различные системы кодирования

4.

Классификационное кодирование
• Классификационное кодирование применяется после
проведения классификации объектов. Различают
последовательное и параллельное кодирование.
• Последовательное кодирование используется для
иерархической классификационной структуры. Суть
метода заключается в следующем: сначала
записывается код старшей группировки 1-го уровня,
затем код группировки 2-го уровня, затем код
группировки 3-го уровня и т.д. В результате
получается кодовая комбинация, каждый разряд
которой содержит информацию о специфике
выделенной группы на каждом уровне
иерархической структуры. Последовательная система
кодирования обладает теми же достоинствами и
недостатками, что и иерархическая система
классификации.

5.

Пример 1. Проведем кодирование информации, классифицированной
с помощью иерархической схемы .
Количество кодовых группировок будет определяться глубиной
классификации и равно 4, Прежде чем начать кодирование,
необходимо определиться с алфавитом, т.е. какие будут
использоваться символы. Для большей наглядности выберем
десятичную систему счисления -10 арабских цифр. Анализ схемы на
рисунке показывает, что длина кода определяется 4 десятичными
разрядами, а кодирование группировки на каждом уровне можно
делать путем последовательной нумерации слева направо.

6.

В общем виде код можно записать как ХХХХ, где Х - значение
десятичного разряда.
Рассмотрим структуру кода, начиная со старшего разряда:
1-й (старший) разряд выделен для классификационного признака
"название факультета" и имеет следующие значения: 1 коммерческий; 2 - информационные системы; 3 - для следующего
названия факультета и т.д.;
2-й разряд выделен для классификационного признака "возраст" и
имеет следующие значения: 1 - до 20 лет; 2 - от 20 до 30 лет; 3 свыше 30 лет;
3-й разряд выделен для классификационного признака "пол" и
имеет следующие значения: 1 - мужчины; 2 - женщины;
4-й разряд выделен для классификационного признака "наличие
детей у женщин" и имеет следующие значения; 1 - есть дети; 2 нет детей, 0 - для мужчин, так как подобной информации не
требуется.
Принятая система кодирования позволяет легко расшифровать
любой код группировки, например:
1310 - студенты коммерческого факультета, свыше 30 лет
мужчины;
2221 - студенты факультета информационных систем, от 20 до 30
лет, женщины имеющие детей.

7.

Параллельное кодирование
используется для фасетной системы классификации. Суть метода
заключается в следующем: все фасеты кодируются независимо
друг от друга; для значений каждого фасета выделяется
определенное количество разрядов кода. Параллельная система
кодирования обладает теми же достоинствами и недостатками,
что и фасетная система классификации.
Пример 2. Проведем кодирование информации,
классифицированной с помощью фасетной схемы .
Количество кодовых группировок определяется количеством
фасетов и равно 4. Выберем десятичную систему счисления в
качестве алфавита кодировки, что позволит для значений
фасетов выделить один разряд и иметь длину кода, равную 4. В
отличие от последовательного кодирования для иерархической
системы классификации в данном метоле не имеет значения
порядок кодировки фасетов. В общем виде код можно записать
как ХХХХ, где Х - значение десятичного разряда. Рассмотрим
структуру кода, начиная со старшего разряда:

8.

1-й (старший) разряд выделен для фасета "кол" и имеет
следующие значения: 1 - мужчины; 2 - женщины;
2-й разряд выделен для фасета "наличие детей у женщин" и имеет
следующие значения: 1 - есть дети; 2 - нет детей; 0 - для мужчин,
так как подобной информации не требуется;
3-й разряд выделен для фасета "возраст" и имеет следующие
значения: 1 - до 20 лет; 2 - от 20 до 30 лет; 3 - свыше 30 лет;
4-й разряд выделен для фасета "название факультета" и имеет
следующие значения 1 - радиотехнический, 2 машиностроительный, 3 - коммерческий; 4 - информационные
системы; 5 - математический и т.д.
Принятая система кодирования позволяет легко расшифровать
любой кол группировки, например:
2135 - женщины в возрасте свыше 30 лет, имеющие детей и
являющиеся студентами математического факультета;
1021 - мужчины возраста от 20 до 30 лет, являющиеся студентами
радиотехнического факультета.

9.

Регистрационное кодирование
Регистрационное кодирование используется для однозначной
идентификации объектов и не требует предварительной
классификации объектов. Различают порядковую и серийнопорядковую систему.
Порядковая система кодирования предполагает
последовательную нумерацию объектов числами натурального
ряда. Этот порядок может быть случайным или определяться
после предварительного упорядочения объектов, например по
алфавиту. Этот метод применяется в том случае, когда
количество объектов невелико, например кодирование
названий факультетов университета, кодирование студентов в
учебной группе.
Серийно-порядковая система кодирования предусматривает
предварительное выделение групп объектов, которые
составляют серию, а затем в каждой серии производится
порядковая нумерация объектов. Каждая серия также будет
иметь порядковую нумерацию. По своей сути серийнопорядковая система является смешанной: классифицирующей и
идентифицирующей. Применяется тогда, когда количество
групп невелико.

10.

Пример 3.
Все студенты одного факультета разбиваются на
учебные группы (в данной терминологии - серии), для
которых используется порядковая нумерация. Внутри
каждой группы производится упорядочение фамилий
студентов по алфавиту и каждому студенту
присваивается номер.

11.

Классификация
информации в организации

12.

Виды информации,
обрабатываемой в компьютере
Числовая
Символьная
Графическая
Звуковая

13.

Формы представления числовой
информации в компьютере
1.
2.
3.
4.
Вопросы:
Позиционные системы счисления.
Перевод чисел из одной системы счисления в
другую.
Формы представления чисел в ЭВМ.
Специальное кодирование. Прямой, обратный
и дополнительный коды.

14.

Системой
счисления
называют
совокупность приемов построения,
обозначения и наименования чисел.
Система счисления характеризуется:
набором символов (цифр): a0, a1, a2, …,a n - 1} –
для записи чисел, т.е. конечный алфавит;
основанием системы «q»;
способом записи (изображения) чисел;
способом чтения (наименования) чисел.

15.

Каждой цифре в записи числа
сопоставляется
определенное
количество, которое называют количественным
эквивалентом
ЦИФРЫ (КЭ).
Количественным эквивалентом
ЧИСЛА называется значение
числа в десятичной системе
счисления.

16.

СИСТЕМЫ СЧИСЛЕНИЯ
• Позиционные системы счисления – это системы , в
которых КЭ любой
цифры зависит от её
местоположения (позиции) в записи числа.
Пример: А10= 373; / З / = 300, / 7 / = 70, / 3 / = 3
• Непозиционными системами счисления называют
системы, в которых КЭ любой цифры не зависит
от её места в записи числа.
Пример: A /pcc/ = XIX; / X / = 10, / I / = 1, / X / = 10
A /pcc/ = CLXXII ; / C/=100, /L/=50, /X/=10 / I / =1

17.

Характеристики позиционных
систем
• При n разрядов целой части и m разрядов в
дробной:
A = a n – 1a n – 2 … a 2 a 1 a 0 , a –1 a – 2 …a – m
где а i – цифра i – го разряда числа;
i – номер разряда.
Позиции имеют номера и называются
разрядами числа.
Количество разрядов для представления чисел
в конкретной ЭВМ ограничено и определяется
разрядной сеткой.

18.

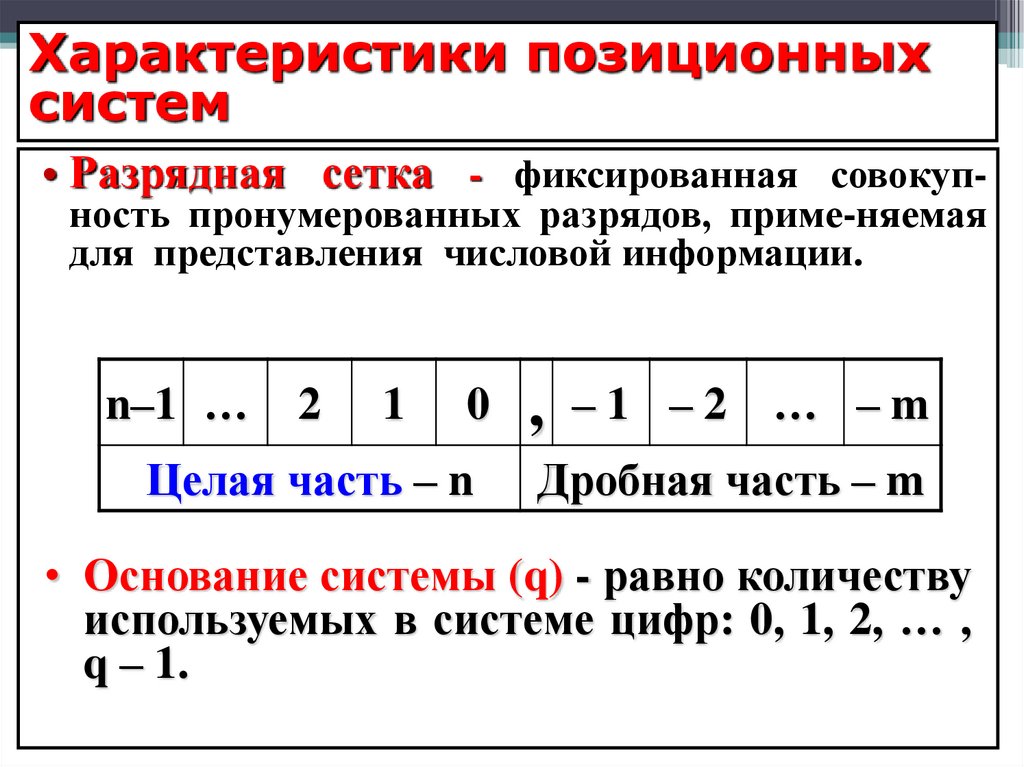
Характеристики позиционных
систем
• Разрядная сетка - фиксированная совокупность пронумерованных разрядов, приме-няемая
для представления числовой информации.
n–1 …
2
1
0
Целая часть – n
,
–1 –2
… –m
Дробная часть – m
• Основание системы (q) - равно количеству
используемых в системе цифр: 0, 1, 2, … ,
q – 1.

19.

Характеристики
позиционных систем
• Вес разряда В i = q i , где i – номер разряда.
Например: Для разрядов в десятичной
системе имеем следующие
веса:
В 0 = 10 0 – единицы,
В 1 = 10 1 – десятки,
В 2 = 10 2 – сотни и т.д.
• Количественный эквивалент цифры (a i):
ai=Вi×ai

20.

Разложение числа по степеням
основания
A(q) = a n – 1 × q n – 1 +…+ a 1× q1 + a 0 × q0 +
+ a –1 × q – 1 + a – m × q – m
где а i – цифра i – го разряда; i – номер разряда; q
– основание системы счисления.
Пример:
А (10) = 628,74
А(10) = 6 × 102 + 2 × 101 + 8 × 100 + 7× 10- 1 +4 × 10 -2

21.

Свойства позиционных систем
• Максимальное число: Amax = qn – q - m
1
…
1
1
1
Целая часть – n
,
1
1
…
1
Дробная часть – m
• Минимальное число: Amin = q -m
• Количество чисел: N = q n + m
• Число разрядов, необходимое для
представления N различных чисел:
k = ] log q N [

22.

Двоичная система счисления
• Двоичная система счисления имеет
основание q = 2 и алфавит, состоящий
из двух цифр 0 и 1.
• Вес разряда вычисляется как Bi = 2 i ,
где i – номер разряда.
• Веса разрядов для n = 5, m = -5
i
5
4
3 2 1 0 -1 -2 -3
-4
-5
1/ 1/ 1/
Bi 32 16 8 4 2 1
2 4 8
1/
16
1/
32

23.

Двоичная система счисления
Достоинства:
совместимость со значением логических функций;
надежность физического представления двоичных
цифр;
наиболее экономичная по затратам оборудования;
простотой реализации операции над числами.
Недостатки:
необходимость и трудоемкость перевода из
10-ой в 2 –ую СС;
трудность восприятия человеком.

24.

Восьмеричная система счисления
Восьмеричная система счисления
имеет основание q = 8 и использует
для представления чисел цифры:
0, 1, 2, 3, 4, 5, 6 и 7.
Веса разрядов восьмеричной
системы:
i
3
2
1
0
-1
-2
-3
Bi 512 64
8
1
1/8 1/64 1/512

25.

Шестнадцатеричная система счисления
• Основание q = 16;
• Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A, B, C, D, E , F.
Веса разрядов шестнадцатеричной
системы:
i
3
2
1
0
Bi 4096 256 16
1
-1
-2
-3
1/16 1/256 1/4096

26.

26
Примеры СС
СС
Десятичная
Двоичная
Восьмеричная
Алфавит
0,1,2…9
0,1
0,1,2,3,
4,5,6,7
Основание
10
2
8
Шестнадцатеричная
0,1,2…9,
A,B,C,D,
E,F
16

27.

Методы перевода чисел из одной
системы счисления в другую
1. Метод непосредственного
замещения.
2. Метод последовательного
деления (умножения) на
основание новой системы
счисления.
3. Поразрядный метод перевода.

28.

Метод непосредственного замещения
Пример 1. Дано:А(2) = 1011,01
Найти: А (10) = ?
1 шаг: А(2)= 1×1011 + 0×1010 + 1×1001 +
+ 1×1000 + 0×10 – 01 + 1×10 – 10
2 шаг: А(10) = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 +
+1 × 2 0 + 0 × 2 – 1 + 1×2 – 2 =
= 8 + 0 + 2 + 1 + 0 +1/4 = 11 1/4

29.

Метод непосредственного замещения
Пример 2.
Дано: А(10) = 22
Найти: А(2) = ?
1 шаг: А(10) = 2∙× 10 1 + 2∙× 10 0 ;
2 шаг: А(2)=10 × 1010 01 + 10 × 10100 =
10100 + 10 = 10110

30.

Метод последовательного деления
Перевод целых чисел
1. Последовательно, сначала исходное
число, затем получающиеся частные
делить на основание новой системы
(действия производить в старой системе).
2. Деление продолжать до получения
частного, меньшего основания новой
системы.
3. Последнее частное и остатки от
деления в каждом шаге записать в
порядке, обратном их получения.

31.

Метод последовательного деления
_157 2
156 78 2
1 78 39 2
0 38 19 2
1 18 9 2
1 8 4
1 4
0
А(10)=157; А(2)=?
2
2 2
2 1
0
а7 а6 а5 а4 а3 а2 а1 а0
ОТВЕТ:
A(2)=10011101

32.

Метод последовательного деления
Перевод дробных чисел
1. Сначала исходное число, затем дробные части, получающиеся в каждом шаге,
произведения умножить на основание
новой системы.
2. Целые части, получившихся произведений, записать цифрами новой системы
счисления в порядке их получения.
3. Вычисления прекращаются, если
достигнута точность вычислений.
(получено значение разряда, вес
которого не больше веса младшего
разряда исходного числа).

33.

Метод последовательного
деления (умножения)
А(10)=0,789; А(2)=?
а1
а2
0, 789
2
1, 578
0, 578
2
1, 156
0, 156
2
0, 312
0, 624
2
1, 248
0, 496
2
0, 992
0, 984
2
1, 968
0, 312
2
0, 624
0, 248
2
0, 496
0, 992
2
1, 984
0, 968
2
1, 936
а3
а4
а5
а6
а7
а8
ОТВЕТ: А(2)= 0,1100100111
а9
а10

34.

Метод последовательного деления
(умножения)
Перевод смешанных дробей
1. Целую часть числа переводим
методом последовательного деления
на основание новой системы.
2.
Перевод дробной части числа
выполняется методом последовательного умножения на основание
новой системы.

35.

Поразрядный метод перевода
Возможен в случае, когда
основание одной системы (p)
является
целой
степенью
основания другой системы (q) :
p=q
k ,
где k – целое число.

36.

Поразрядный метод перевода
Для перевода двоичного числа в
восьмеричную (шестнадцатеричную)
систему достаточно разбить его
вправо и влево от запятой на триады
(тетрады) и заменить их цифрами
восьмеричной (шестнадцатеричной)
системы.
Если при разбиении крайние
группы окажутся неполными, их
следует заполнить нулями.

37.

Поразрядный метод перевода
Из восьмеричной
цатеричной) системы в
перевод выполняется
каждой восьмеричной
цатеричной) цифры
триадой (тетрадой).
(шестнаддвоичную
заменой
(шестнаддвоичной

38.

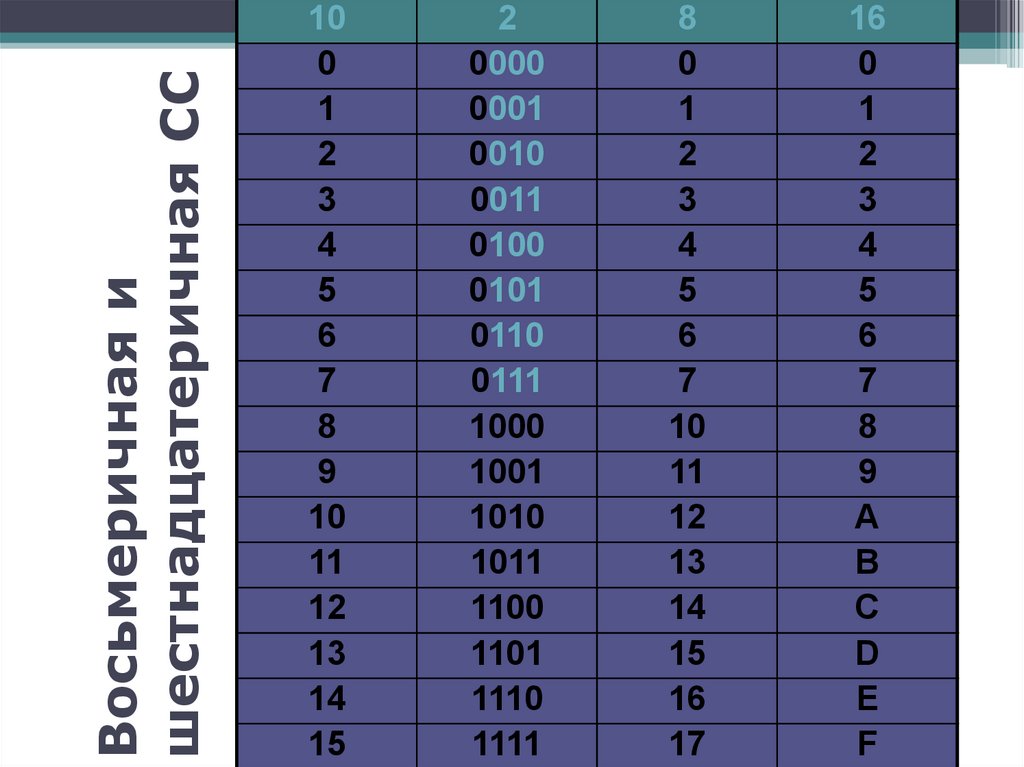
Восьмеричная и
шестнадцатеричная СС
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
8
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
38

39.

39
Быстрый перевод из 2-й в
8-ю и 16-ю СС
001001100111011000001
1
1
4
7
3
0
1
01001100111011000001
4
C
E
C
1

40.

• Разрядная сетка - фиксированная
совокупность
пронумерованных
разрядов,
применяемая
для
представления числа.
Зн n–1 …
1
0
Целая часть – n
,
–1 –2
… –m
Дробная часть – m
• Основание системы (q) - равно
количеству
используемых
в
системе цифр: 0, 1, 2, … , q – 1.

41.

Формы представления чисел
•естественная форма или форма
с фиксированной запятой;
•нормальная форма или с
плавающей запятой.

42.

Естественная форма
представления чисел
(с фиксированной запятой)
Целые числа:
Зн an-1 an-2 an-3 an-4 …….. a0

43.

Естественная форма
представления чисел
(с фиксированной запятой)
Дробные числа :
Зн, a-1
a-2
a-3 …...…….
a-m

44.

Естественная форма
представления чисел
(с фиксированной запятой)
Смешанная форма:
Зн an-1 an-2 …. a0
, a-1
a-2 a-3
.... a-m

45.

Нормальная форма
представлений чисел
Число
представленное
в
нормальной форме, записывается
в следующем виде:
А = ±Ма×q
±P
,
где m – мантисса числа;
q – основание системы
счисления;
p – порядок числа.

46.

Нормальная форма
представлений чисел
Число называется нормализованным,
если модуль мантиссы больше нуля и
меньше единицы:
0< |m|< 1
Пример:
N10 = 216,32
в нормализованном виде:
N10 = 0,21632 · 103
Числа в памяти ЭВМ обычно
хранятся в нормализованном виде.

47.

Нормальная форма представления
чисел с нормализованной мантиссой
Знак
Мантисса
,
мантиссы
числа
Знак
порядка
Порядок
числа
ЗнМ , М-1 М-2 … М- R ЗнП ПL-1 ПL- 2 .... П0
где
R – разрядность мантиссы,
L – разрядность порядка

48.

Особенности и ограничения при
представлении двоичных чисел в ЭВМ
1. Для знака в сетке выделяется
специальный знаковый разряд:
для «+» 0
для «-» 1
2. Вычитание чисел заменяется алгебраическим суммированием:
A – B = A + (-B)
3. При сложении чисел обработка всех
разрядов (в т. ч. и знаковых) осуществляется
по
единым
формальным
правилам.

49.

Взаимосвязь
прямого кода(ПК),
обратного кода(ОК),
дополнительного кода(ДК)
и правила их получения

50.

ПРЯМОЙ КОД
Прямой код [X]пк числа Х образуется
добавлением к Х, взятому без знака, одного
знакового разряда слева.
X при X ≥ 0; знаковый = 0
[X]ПК=
1+|X| при X< 0; знаковый = 1
Пример. А = - 0,1011
В = + 0,0101
Тогда: [A]ПК = 1, 1011
[B]ПК = 0, 0101

51.

Правила получения ОК
ОК положительных чисел равен ПК и
для дробных чисел совпадает с самим
числом.
• Для получения ОК отрицательных
чисел
необходимо проинвертировать
все разряды числа, представленного в
ПК, за
исключением
знакового (в
знаковом разряде оставить 1).
Пример:
[A] ПК = 1,1011
[A]ОК = 1, 0100
[B] ПК = 0,1011
[B] ОК = 0,1011

52.

Правила получения ДК
ДК положительных чисел равен
прямому коду.
• Для получения ДК
отрицательных чисел необходимо
проинвертировать все разряды
числа, представленного в ПК, за
исключением знакового, и добавить
единицу в младший разряд (в
знаковом разряде оставить 1).

53.

Восьмеричная и
шестнадцатеричная СС
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
8
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F

54.

Быстрый перевод из 2-й в
8-ю и 16-ю СС
001001100111011000001
1
1
4
7
3
0
1
01001100111011000001
4
C
E
C
1

55.

Формы представления
чисел
естественная форма
или форма с фиксированной запятой
+00721,35500; +00000,00328;
-10301,20260
нормальная форма
или форма с плавающей запятой
+0,721355х103; +0,328х10-2;
-0,103012026х105

56.

В языке программирования Turbo Pascal используются, например,
такие целые типы данных:
Тип данных Размер памяти Количество чисел
Диапазон
Byte
1 байт
28 = 256
0 ..255
ShortInt
1 байт
28 = 256
-128 .. 127
Word
2 байта
216 = 65 536
0 .. 65 535
Integer
2 байта
216 = 65 536
-32 768 .. 32 767
Пояснения к таблице. Типы ShortInt и Integer используются для записи
целых со знаком, т.е. старший бит хранит знак числа; типы Byte и Word
используются для записи целых без знака (неотрицательных); 1 байт = 8
бит; используя n бит можно записать 2n различных чисел (доказывается
по индукции). Покажем, что максимальное число, которое можно
представить, используя n бит равно (2
n – 1).

57.

Для правильной интерпретации содержимого памяти нужно знать,
какой тип данных в ней храниться, т.к. по «внешнему виду» отличить
один тип от другого нельзя. Пусть, например, 1 байт памяти содержит
следующие данные: 1001 1101. Если это число типа Byte, то оно равно
27+24+23+22+20= 128+16+8+4+1=15710. Если это целое число со знаком
типа ShortInt, то для его определения надо инвертировать код: 0110
0010, затем прибавить 1: получим 0110 0011, т.е. 26+25+21+20=
64+32+2+1 = 9910, значит, данный байт содержит число - 99.

58.

Система представления чисел
с плавающей точкой
F(b, t, L, U)
Такая система используется для записи вещественных чисел в
современных ЭВМ. Здесь b – основание системы, t – количество разрядов
мантиссы, L , U – пределы изменений значений показателей порядка
чисел в этой системе. Пример числа, записанного в виде числа с
плавающей точкой: 0.31562781*105; здесь 0.31562781 – мантисса числа,
5 – его порядок. Это число в «обычной», позиционной записи выглядит
как
31562.781. Такой способ представления чисел позволяет компактно
записывать числа из широкого диапазона значений, например:
0.4671*10-15, или 0.8965*1012.

59.

Кодирование символов
1 символ = 1 байт
Американский стандартный код
обмена информацией
American Standard Code for
Information Interchange
ASCII

60.

Таблица ASCII- кодов

61.

Другие кодировки
CP866 (DOS-альтернативная)
CP1251 (RFC1489) (Windows-1251)
KOI-8R (ISO-IR-111; ГОСТ 19768-74)
Macintosh Cyrillic
ISO-8859
UNICODE (1 символ-2 байта)

62.

Кодирование изображения
Пиксел – маленькая цветная "точка"
pixel – Picture Element,
(элемент картинки)
Разрешение – характеристика
устройства вывода, показывающая
плотность расположения пикселов
dpi – Dot Per Inch (точек на дюйм)

63.

Два вида компьютерной
графики
Растровая – изображение строится из
точек (PhotoShop)
Векторная графика - изображение
строится не из точек, а из графических
примитивов: простейших
геометрических фигур (линий,
прямоугольников, окружностей, дуг и
пр.). В этом случае кодируется не сам
рисунок, а правила его построения.
(CorelDraw, AutoCad)

64.

Сравнительная характеристика
Растровая
Векторная
Построение
Из пикселей (точек)
Из графических
примитивов
По пикселям
Редактирование
Каждый объект в
отдельности
Качество изображения
Возможны полутоновые Всегда существует четкая
переходы
граница между объектами
(искусственный вид)
Изображение близко к
художественному

65.

Сравнительная характеристика
Растровая
Векторная
Масштабированиe
Портит изображение
Без потери качества
Объем занимаемой памяти
Много занимает места
Существенно меньше
Применение
Художественная
графика
Чертежи, схемы,
эмблемы

66.

Информационный объём растрового
графического изображения
Расчёт информационного объёма растрового графического изображения (количества
информации, содержащейся в графическом изображении) основан на подсчёте
количества пикселей в этом изображении и на определении глубины цвета
(информационного веса одного пикселя).
Итак, для расчёта информационного объёма растрового графического изображения
используется формула V=K*i, где V – это информационный объём растрового
графического изображения, измеряющийся в байтах, килобайтах, мегабайтах; K –
количество пикселей (точек) в изображении, определяющееся разрешающей
способностью носителя информации (экрана монитора, сканера, принтера); i – глубина
цвета, которая измеряется в битах на один пиксель.
Глубина цвета задаётся количеством битов, используемым для кодирования цвета
точки.
Глубина цвета связана с количеством отображаемых цветов формулой
N=2i, где N – это количество цветов в палитре, i – глубина цвета в битах на один пиксель.

67.

Рассмотрим примеры задач.
1) Видеопамять компьютера имеет объем 512Кб, размер графической сетки 640Х200, в палитре 16 цв
Дано:
K=640´200=128000 пикселей;
N=16 цветов;
Vвп=512 Кб
Решение:
Используем формулы
V=K*i;
N=2i;
m= Vвп/V, где m – это количество страниц экрана
16=24 ; i=4 бита/пиксель;
K=640*200=128000пикселей
V=128000*4=512000бит=64000байт=62,5Кб на один экран
M=512/62,5=8 страниц
Ответ: 8 полных страниц экрана можно одновременно хранить в видеопамяти компьютера.
2) В результате преобразования растрового графического изображения количество цветов
уменьшилось с 256 до 16. Как при этом изменится объем видеопамяти, занимаемой изображением?
Дано:
N1=256 цветов;
N2=16 цветов;

68.

3) Сканируется цветное изображение стандартного размера А4 (21*29,7 см).
Разрешающая способность сканера 1200dpi и глубина цвета 24 бита. Какой
информационный объём будет иметь полученный графический файл?
Дано:
i=24 бита на пиксель;
S= 21см*29,7 см
D=1200dpi (точек на один дюйм)
Решение:
Используем формулы
V=K*i;
1дюйм=2,54 см
S=(21/2,54)*(29,7/2,54)=8,3дюймов*11,7дюймов
K=1200*8,3*1200*11,7=139210118 пикселей
V=139210118*24=3341042842бита=417630355байт=407842Кб=398Мб
Ответ: объём сканированного графического изображения равен 398 Мегабайт

69.

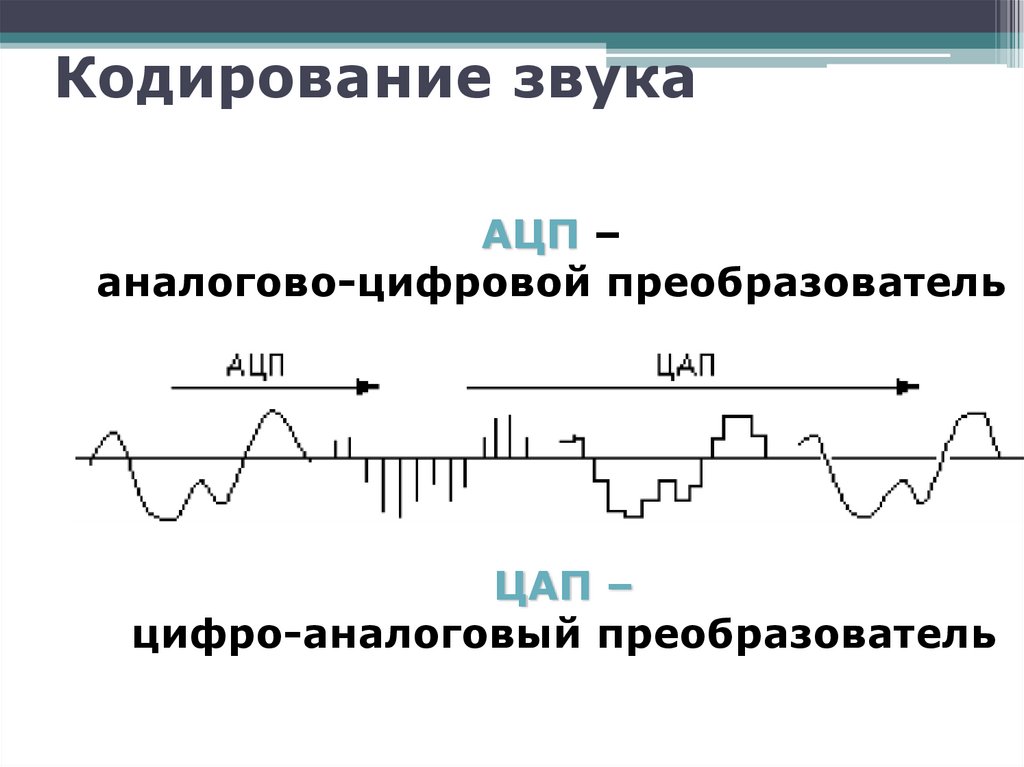
Кодирование звука
АЦП –
аналогово-цифровой преобразователь
ЦАП –
цифро-аналоговый преобразователь

70.

Звук представляет собой звуковую волну с непрерывно меняющейся
амплитудой и частотой.
Чем больше амплитуда сигнала, тем он громче для человека, чем
больше частота сигнала, тем выше тон.
Оцифровка звука - превращение в последовательность электрических
импульсов (двоичных нулей и единиц).
В процессе кодирования непрерывного звукового сигнала производится
его временная дискретизация. Непрерывная звуковая волна
разбивается на отдельные маленькие временные участки, причем для
каждого такого участка устанавливается определенная величина
амплитуды.
Таким образом, непрерывная зависимость амплитуды сигнала от
времени A(t) заменяется на дискретную последовательность уровней
громкости. На графике это выглядит как замена гладкой кривой на
последовательность "ступенек".

71.

Каждой "ступеньке" присваивается значение уровня громкости звука, его код (1, 2,
3 и так далее). Уровни громкости звука можно рассматривать как набор возможных
состояний, соответственно, чем большее количество уровней громкости будет
выделено в процессе кодирования, тем больше объем данных, и тем более
качественным будет звучание.
Разрядность звуковой карты (R) - это количество распознаваемых дискретных
уровней сигналов.
Количество различных уровней сигнала (состояний при данном кодировании) можно
рассчитать по формуле: N=2I, где I - глубина звука.
8, 16-битные звуковые карты обеспечивают 256, 65536 уровней сигнала.
Очевидно, что 16-битные звуковые карты точнее кодируют и воспроизводят звук, чем
8-битные.
Частота дискретизации (η) - это количество измерений уровня сигнала в единицу
времени.
Чем большее количество измерений производится за 1 секунду (чем больше частота
дискретизации), тем точнее процедура двоичного кодирования.
Одно измерение в секунду соответствует частоте 1 Гц (Герц).
1000 измерений в секунду - 1 кГц.
Частота, с которой происходит выборка сигналов, может принимать значения от 5,5
кГц до 48 кГц.

72.

Качество двоичного кодирования звука определяется
глубиной кодирования и частотой дискретизации.
Качество звука в дискретной форме может быть очень плохим (при 8 битах и
5,5 кГц) и очень высоким (при 16 битах и выше 40 кГц), так же как
радиотрансляция и аудио CD.
Формула для расчета объема цифрового моноаудиофайла
(для стереофайла объем увеличиваем в 2 раза)
V = R · t ·η,
где V - информационный объем аудиофайла,
R - разрядность звуковой карты,
t - время звучания аудиофайла,
η - частота дискретизации
Пример.
Оценить объем звуковых данных.
Длительность звучания 10с,
частота дискретизации 22,05 кГц,
разрядность - 8 бит.
Все перемножаем.

73.

Кодирование звука
MIDI
(Musical Instrument Digital Interface цифровой интерфейс для
музыкальных инструментов) –
стандарт, определяющий систему
кодов нотной записи, а также
физические характеристики линий
передачи, протоколы связи и пр.