Электрофизические свойства проводниковых материалов

1. Электрофизические свойства проводниковых материалов

• План лекции:
• 1. Физическая природа электропроводности
металлов
• 2. Зависимость электропроводности металлов от
температуры
• 3. Влияние примесей и дефектов структуры на
удельную проводимость металлов
• 4. Электрические свойства металлических сплавов
• 5. Сопротивление проводников на высоких частотах

2. Физическая природа электропроводности металлов

• В основе классической электронной теории металлов лежит
представление об электронном газе, состоящем из свободных
электронов. Электронный газ считается идеальным газом, т. е.
движение электронов подчиняется законам классической
статистики Максвелла-Больцмана.
• При однократной ионизации атомов число свободных электронов
равно числу атомов:
• n= (d / A) N0
• где d – плотность металла; А – атомная масса; N0 – число
Авогадро.
• Электроны в металле находятся в состоянии теплового
хаотического движения, их средняя кинетическая энергия:
• (m0ū2) / 2 = (3 kT) / 2
• где m0 - масса электрона, ū – средняя скорость теплового
движения, k-постоянная Больцмана. При T = 300 K ū ≈ 105 м/с.

3.

• При приложении внешнего электрического поля к металлу
происходит упорядочение движения электронов и увеличение
их скорости на некоторую величину ̅v , т. е. возникает
электрический ток. Плотность тока (A/м2):
• J = e n ̅v,
• где ̅v – скорость направленного движения электрона (скорость
дрейфа).
2
• В медном проводнике при j = 106 a/м ̅v ≈ 10–4 м/с, т. е. ̅v << ū.
• Электроны при движении сталкиваются с узлами
кристаллической решетки. Между столкновениями они
двигаются с ускорением, которое придает им электрическое
поле:
• а = (e E) / m0 ,
• где m0 – масса электрона; E – напряженность электрического
поля.
• Расстояние, которое проходит электрон между столкновениями
с узлами решетки, называется длиной свободного пробега ¯ɭ

4.

• К концу свободного пробега дрейфовая скорость
электрона ̅v = max, после столкновения с узлом
кристаллической решетки скорость электрона
уменьшается до нуля, а кинетическая энергия
электрона передается кристаллической решетке.
• Отсюда: ̅v = vmax / 2 или:
• ̅v = (еЕ / 2m0)Ʈ0 ,
• где Ʈ0 – время свободного пробега электрона.
• Т.к. ̅v << ū, то при расчете Ʈ0 увеличение скорости за
счет дрейфа можно не учитывать:
• Ʈ0 = ¯ɭ / ū ,
• где ¯ɭ средняя длина свободного пробега электрона.

5.

• Подстановка полученных соотношений в формулу для
плотности тока приводит к следующему результату:
• J = [(e2n¯ɭ ) / (2 m0 ū)] ͯ Е = Ɣ ͯ Е,
• т.е. плотность тока пропорциональна напряженности
электрического поля, а это есть аналитическое выражение
закона Ома.
• При рассмотрении действия электрического поля на всю
совокупность свободных электронов пришли к выводу, что
средняя дрейфовая скорость электронов оказывается в двое
больше, поэтому выражение для удельной проводимости
принимает вид:
• Ɣ = (e2n¯ɭ ) / ( m0 ū)

6.

• Концентрация свободных электронов в чистых
металлах различается незначительно.
• Проводимость определяется в основном длиной
свободного пробега l, которая зависит от вида и
строения металла – химической природы атомов и
типа кристаллической решетки.
• Кристаллическая решетка металлов может быть
искажена под действием таких видов обработки, как:
• - пластическая деформация (кручение, вытяжение,
наклеп) увеличивает сопротивление на несколько
процентов;
• -термическая закалка приводит к уменьшению
длины свободного пробега и увеличению удельного
сопротивление металлов.
• В свою очередь, процесс рекристаллизации (отжига)
уменьшает сопротивление до исходного уровня.

7.

• Представления о свободных электронах
позволяют
легко
прийти
к
экспериментальному
закону
Видемана–
Франца, устанавливающему связь между
проводимостью
и
теплопроводностью
металла.
• Электроны в металле переносят не только
электрический заряд, но и выравнивают в
нем температуру, обеспечивая высокую
теплопроводность.
• Благодаря высокой концентрации свободных
электронов, электронная теплопроводность
преобладает над другими механизмами
переноса теплоты:

8.

• т.е. отношение коэффициента теплопроводности к
удельной проводимости металла при данной
температуре есть величина постоянная, не
зависящая от природы проводника.
• Отсюда, в частности, следует, что хорошие
проводники электрического тока являются и
хорошими проводниками теплоты.
• Константа L0 получила название числа Лоренца.

9. Зависимость электропроводности металлов от температуры

• Электрон при столкновении с атомом передает
кинетическую энергию кристаллической решетке и
теряет скорость. Это явление носит название
рассеяния на узлах кристаллической решетки, или
тепловое рассеяние.
• В чистых металлах единственной причиной,
ограничивающей
длину
свободного
пробега
электронов, являются тепловые колебания атомов в
узлах кристаллической решетки.
• С ростом температуры амплитуда тепловых
колебаний атомов увеличивается, что приводит к
увеличению рассеяния электронов и повышает
электрическое сопротивление металла:

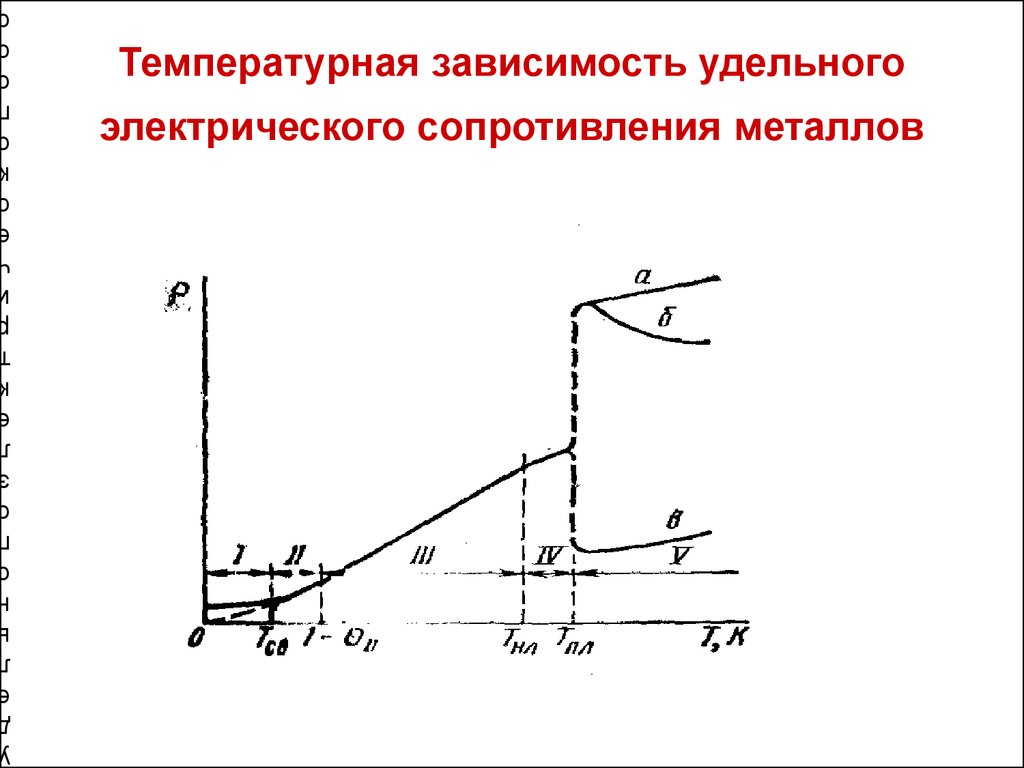
10. Температурная зависимость удельного электрического сопротивления металлов

г
г

11.

На кривой температурной зависимости электрического
сопротивления металлов можно выделить несколько
участков:
• I. 1) - ρ стремится к 0 вблизи 0К для металлов с совершенной
структурой;
2) – ρ ≠ 0 вблизи 0К для металлов с несовершенной
структурой;
3) – ρ снижается до 0 выше 0К для сверхпроводников.
• II. Температурный интервал в котором ρ ≈ Т5 (4-6) ;
Тд- температура Дебая, при которой ρ ≈ Т1. для большинства
металлов Тд = (400 – 450)К.
(Температура Дебая определяет max частоту тепловых колебаний, которые
могут возбуждаться в кристалле и зависит от сил связи между узлами
решетки. При Т > Тд удельное сопротивление металлов изменяется
линейно с изменением температуры).
III. Линейная зависимость ρ от температуры практически до
Тпл кроме ферромагнитных металлов.
IV. Отступление от линейной зависимости у ряда металлов.
V. При температуре плавления ρ повышается в 1,5 – 2 раза у
большинства металлов.

12. Температурная зависимость удельного электрического сопротивления металлов. Правило Маттиссена

• Причинами рассеяния электронных волн в металле являются не
только тепловые колебания узлов кристаллической решетки,
но и статические дефекты структуры.
• Рассеяние на статических дефектах структуры не зависит от
температуры.
• Поэтому по мере приближения температуры к абсолютному
нулю сопротивление реальных металлов стремится к
некоторому постоянному значению, называемому остаточным
сопротивлением.
• Согласно эмпирически установленному правилу Маттиссена,
удельное сопротивление реальных металлов представляет
собой сумму двух составляющих:
• ρ = ρт + ρост

13.

• т. е. полное сопротивление металла есть сумма
сопротивления, обусловленного рассеянием электронов на
тепловых колебаниях узлов кристаллической решетки, и
остаточного сопротивления, обусловленного рассеянием
электронов на статических дефектах структуры.
• Исключение из этого правила составляют сверхпроводящие
металлы, в которых сопротивление исчезает ниже некоторой
критической температуры.
• Наиболее существенный вклад в остаточное сопротивление
вносит рассеяние на примесях, которые всегда присутствуют в
реальном проводнике либо в виде загрязнения, либо в виде
легирующего (т.е. преднамеренно вводимого) элемента.
• Следует заметить, что любая примесная добавка приводит к
повышению ρ, даже если она обладает повышенной
проводимостью по сравнению с основным металлом.

14. Правило Маттиссена для сплавов

• Распределение атомов примеси по узлам кристаллической
решетки или в междуузлиях приводит к сильному рассеянию
электронов на примесях.
• Полное удельное электросопротивление металла со
статическими дефектами (примесями) определяется правилом
Матиссена
• ρспл = ρт + ρост
• При этом величина ρост значительно больше ρт и практически
не зависит от температуры Т, поэтому температурная
зависимость удельного сопротивления сплава ρ = f(Т)
характеризуется более слабым изменением, чем у чистого
металла.
• Температурный коэффициент удельного сопротивления αρт
сплава, в отличии от αρт чистого металла, определяется
только относительным изменением тепловой составляющей
удельного сопротивления Δ ρт / ρ, обусловленной рассеянием
электронов на тепловых колебаниях решетки, происходящим
при изменении температуры ΔТ, и выражается соотношением
• α ρт = (Δ ρт / ρ) ͯ (1/ Δ Т)

15. Электрические свойства металлических сплавов

• Металлическим сплавом называется материал,
полученный сплавлением двух или более металлов
или металлов с неметаллами, и обладающий
металлическими свойствами.
• Компоненты сплава- вещества, которые образуют
сплав.
• Фаза - однородная часть сплава, характеризующаяся
определенным составом, строением и отделенная от
других частей сплава поверхностью раздела.
• Структура - форма размер и характер взаимного
расположения фаз в металлах и сплавах.

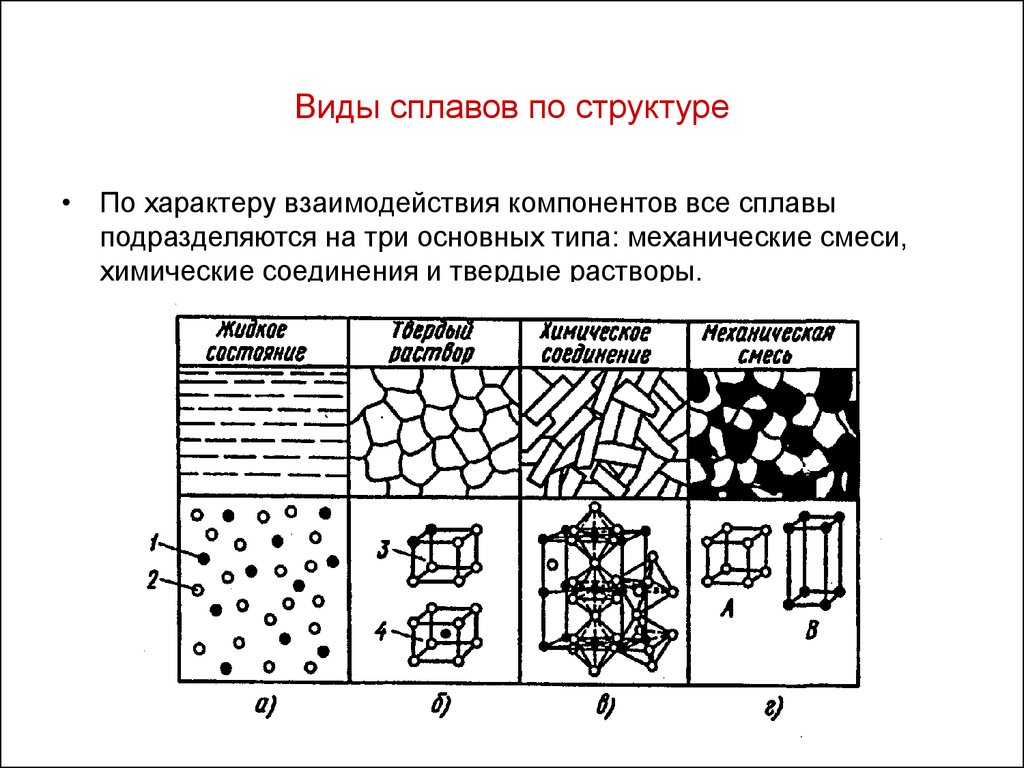
16. Виды сплавов по структуре

• По характеру взаимодействия компонентов все сплавы
подразделяются на три основных типа: механические смеси,
химические соединения и твердые растворы.

17. Твердый раствор

• При образовании твердого раствора атомы одного
компонента растворяются в кристаллической
решетке другого, он имеет однородную структуру и
одну кристаллическую решетку.
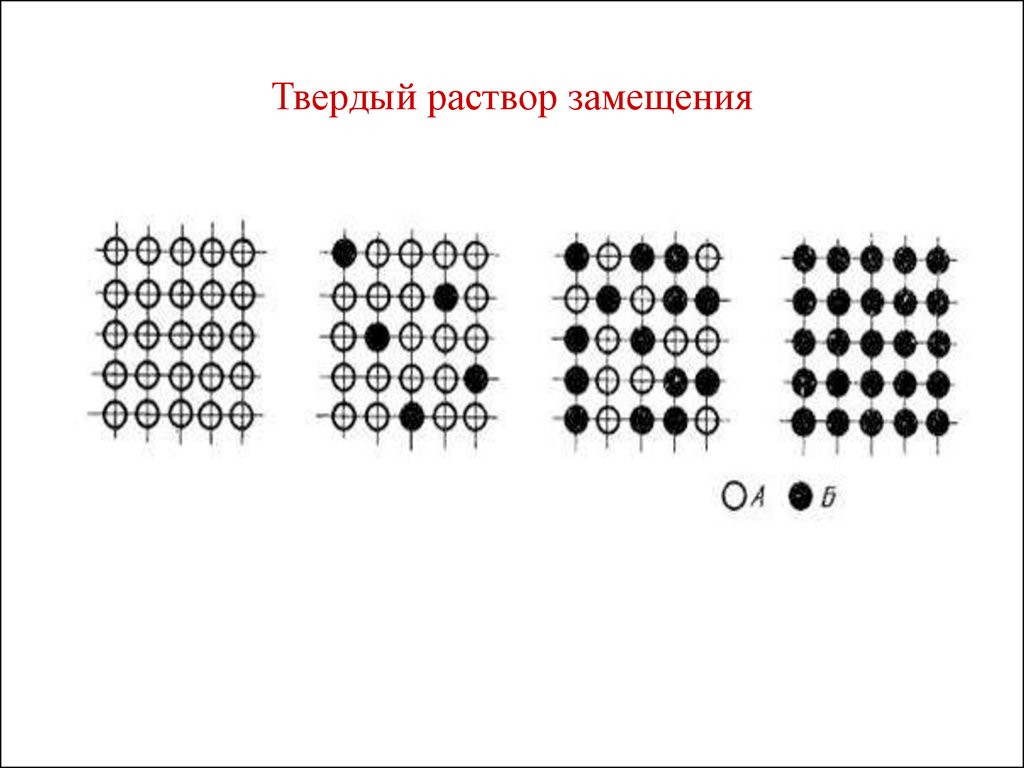
• Твердые растворы замещения образуются в
результате замещения атомов в узлах
кристаллической решетки одного компонента
атомами второго, могут быть с неограниченной
(диапазон концентраций) и ограниченной (строгая
процентная концентрация) растворимостью.
• Твердые растворы внедрения образуются, когда
атомы растворенного компонента внедряются в
кристаллическую решетку компонента –
растворителя между ее узлами.

18. Твердый раствор замещения

19.

• Химическое соединение образуется когда компоненты сплава
А и В вступают в химическое взаимодействие. При этом состав
сплава соответствует его химической формуле AmBn
• .
• Химическое соединение имеет свою кристаллическую решетку,
которая отличается от кристаллических решеток компонентов.
Химические соединения имеют однородную структуру,
состоящую из одинаковых по составу и свойствам зерен.
• Механическая смесь двух компонентов А и В образуется, если
они не способны к химическому взаимодействию или взаимному
растворению. Каждый компонент при этом кристаллизуется в
свою кристаллическую решетку.
• Структура механических смесей неоднородная, состоящая из
отдельных зерен компонента А и компонента В.
• Свойства механических смесей зависят от количественного
соотношения компонентов: чем больше в сплаве данного
компонента, тем ближе к его свойствам свойства смеси.

20. Сопротивление проводников на высоких частотах

• При высоких частотах переменного электрического тока
наблюдается неравномерное распределение электрического
тока по сечению проводника.
• Максимальная плотность тока находится на поверхности, затем
она уменьшается вглубь проводника. Это явление получило
название поверхностного эффекта, или скин-эффекта.
Объясняется это действием на проводник своего же магнитного
поля.
• Изменение магнитного потока ведет к появлению ЭДС самоиндукции, которая имеет направление, противоположное току в
проводнике, и тормозит его изменение согласно закону Ленца.
• Так как потокосцепление максимально в центре проводника,
здесь же максимум ЭДС самоиндукции, что и приводит к
ослаблению тока в его центральных частях.

21.

С увеличением частоты тока «вытеснение» его к поверхности
увеличивается. Можно рассчитать плотность тока на глубине z по
уравнению
• jz = J0 exp (-z/Δ) ,
где J0 – плотность тока на поверхности;
Δ – глубина проникновения поля в проводник (скин-слой),
• Δ=√2/ (γ µ ω),
где Ɣ –удельная проводимость; µ-магнитная проницаемость;
ω-частота.
Увеличение магнитной проницаемости и удельной проводимости
материала усиливает скин-эффект.
При высоких частотах j во всех сечениях, кроме небольшого
поверхностного слоя, практически равно нулю. В связи с этим R
провода на переменном токе больше R провода на постоянном токе.
Коэффициент увеличения сопротивления материала при скинэффекте может быть рассчитан по формуле
• КR = d / 4 Δ,
где d – диаметр провода. Формула справедлива при Δ << d.
КR может достигать 1000 (сталь) и более.

22.

Для медного провода:
При частоте
50 Гц Δ = 9,34 мм;
10 кГц Δ = 0,66 мм ;
1 МГц Δ = 0,066 мм ;
10 МГц Δ = 0,021 мм.
Для борьбы со скин-эффектом применяют проводники
различного сечения: плоские (в виде лент), трубчатые (полые
внутри), наносят на поверхность проводника слой металла с
более низким удельным сопротивлением.
• Так, в ВЧ аппаратуре используют посеребрённые медные
контуры, в высоковольтных линиях электропередач применяют
провод в медной либо алюминиевой оболочке со стальным
сердечником.
• Также с целью подавления скин-эффекта используют систему
из нескольких переплетённых и изолированных проводов —
литцендрат.
• В СВЧ оборудовании применяют колебательные контуры особой
формы: объёмные резонаторы и специфические линии
передач —волноводы.