Similar presentations:
Запросы для поисковых систем с использованием логических выражений
1.
Информатика и ИКТЗапросы для поисковых систем с
использованием логических
выражений
2.
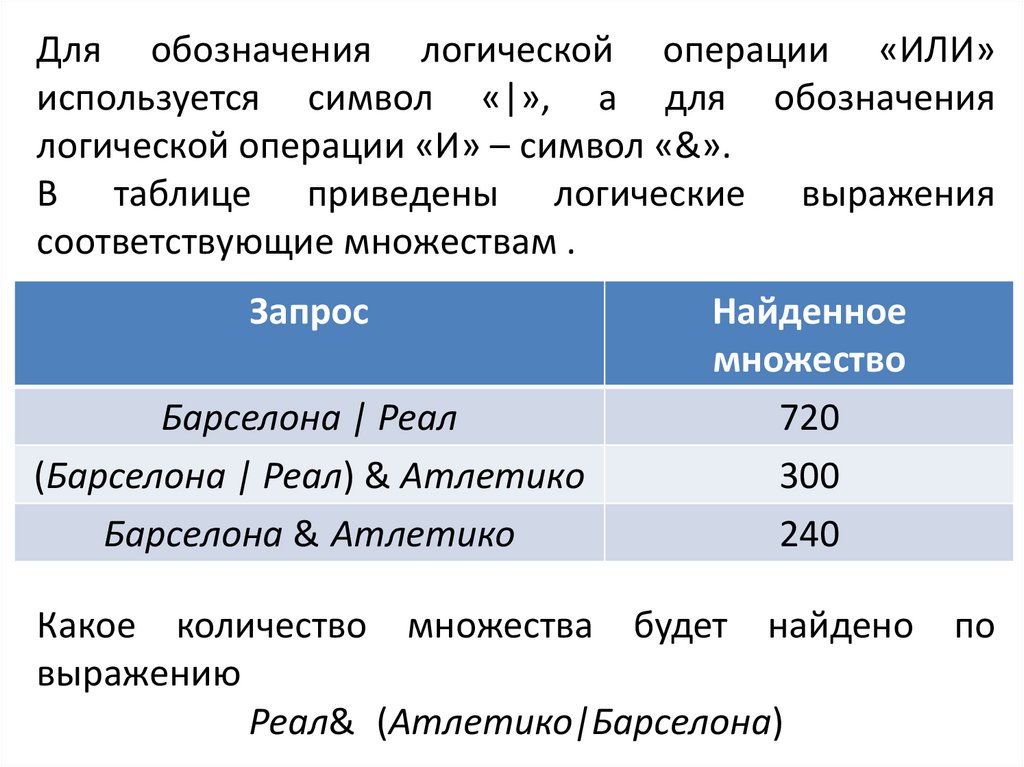
Для обозначения логической операции «ИЛИ»используется символ «|», а для обозначения
логической операции «И» – символ «&».
В таблице приведены логические выражения
соответствующие множествам .
Запрос
Барселона | Реал
(Барселона | Реал) & Атлетико
Барселона & Атлетико
Найденное
множество
720
300
240
Какое количество множества будет найдено по
выражению
Реал& (Атлетико|Барселона)
3.
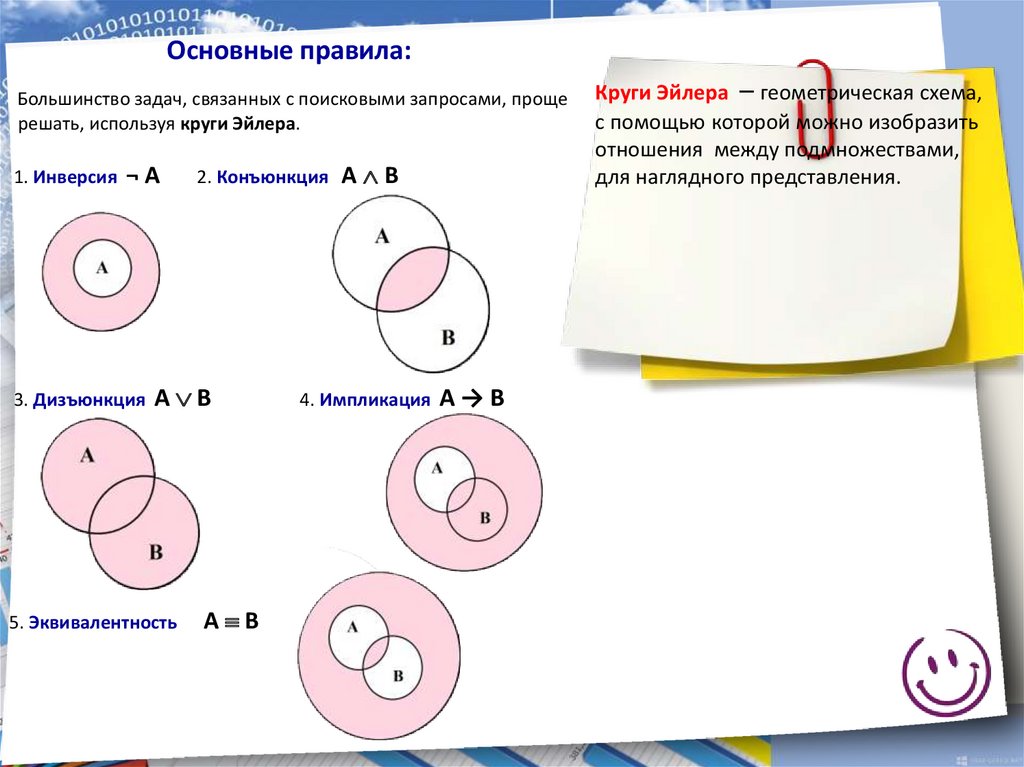
Основные правила:Большинство задач, связанных с поисковыми запросами, проще
решать, используя круги Эйлера.
1. Инверсия
¬A
3. Дизъюнкция
2. Конъюнкция
A B
5. Эквивалентность
A B
A B
4. Импликация
A→B
Круги Эйлера – геометрическая схема,
с помощью которой можно изобразить
отношения между подмножествами,
для наглядного представления.
4.
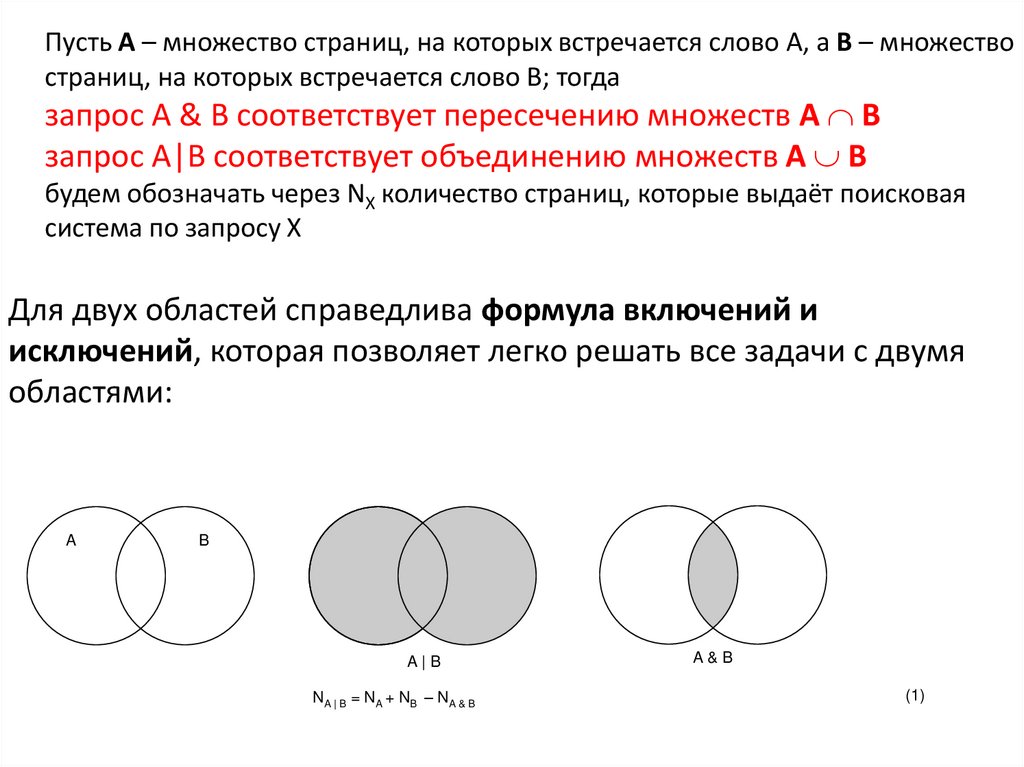
Пусть A – множество страниц, на которых встречается слово A, а B – множествостраниц, на которых встречается слово B; тогда
запрос A & B соответствует пересечению множеств A B
запрос A|B соответствует объединению множеств A B
будем обозначать через NX количество страниц, которые выдаёт поисковая
система по запросу X
Для двух областей справедлива формула включений и
исключений, которая позволяет легко решать все задачи с двумя
областями:
A
B
A|B
NA | B = NA + NB – NA & B
A&B
(1)
5.
Задача1 на два множестваВ таблице приведены запросы и количество страниц, которые нашел поисковый
сервер по этим запросам в некотором сегменте Интернета:
Количество страниц
Запрос
(тыс.)
торты | пироги
12000
торты & пироги
6500
пироги
7700
Сколько страниц (в тысячах) будет найдено по запросу
торты
6.
Запишем условие задачи в наших обозначенияхКоличество страниц
(тыс.)
Запрос
Дано:
N1+ N2 +N3 =12000
торты | пироги
12000
торты & пироги
6500
N2 =6500
пироги
7700
N2 +N3 = 7700
Торты
Пироги
Найти: N1+ N2
Решение:
N1
N2
N3
N3 =7700 – 6500=1200
N1+ N2 = 12000 – 1200 = 10800
7.
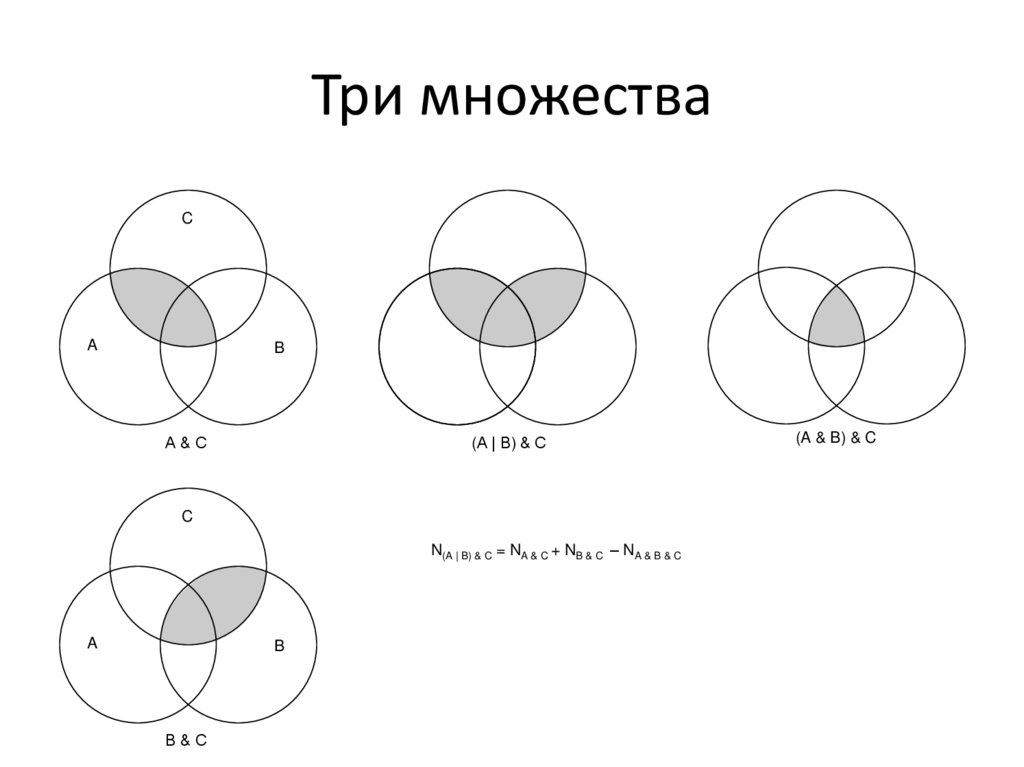
Три множестваC
A
B
A&С
(A | B) & С
C
N(A | B) & C = NA & C + NB & C – NA & B & C
A
B
B&С
(A & B) & C
8.
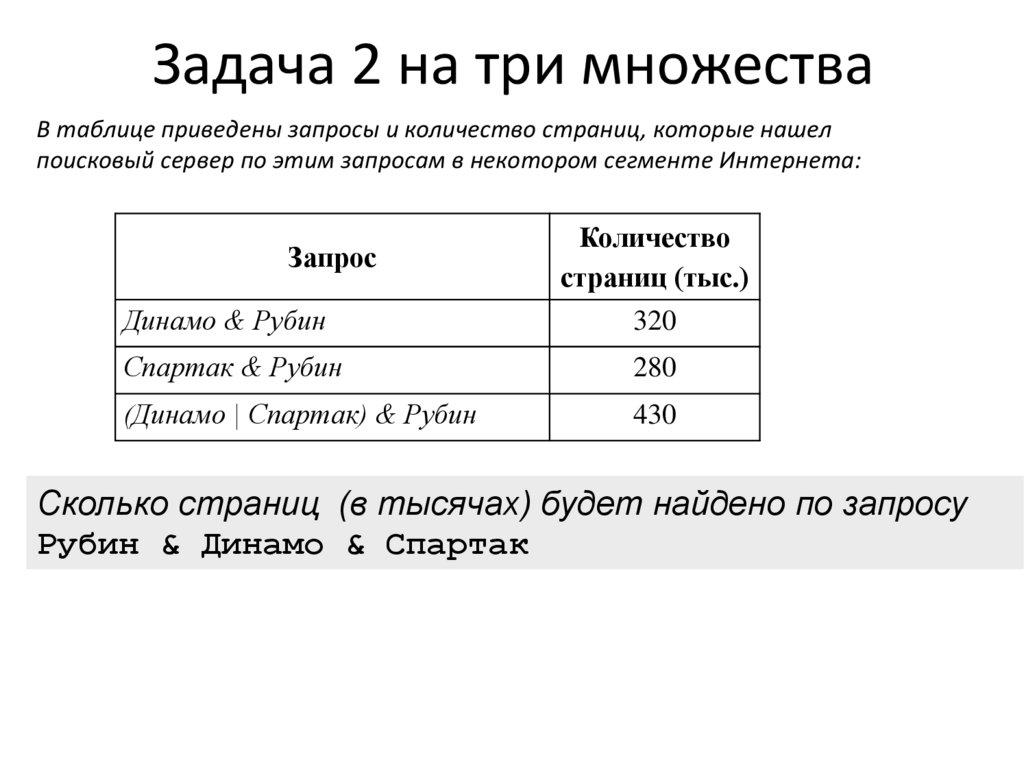
Задача 2 на три множестваВ таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте Интернета:
Запрос
Количество
страниц (тыс.)
Динамо & Рубин
320
Спартак & Рубин
280
(Динамо | Спартак) & Рубин
430
Сколько страниц (в тысячах) будет найдено по запросу
Рубин & Динамо & Спартак
9.
Запишем условие задачи в наших обозначенияхКоличество
страниц (тыс.)
Запрос
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) &
Рубин
Д
Р
N1
N2
N5
N4
N7
С
N3
N6
320
280
430
Дано:
N2 + N4 = 320
N4 + N6 = 280
N2+ N4 +N6 = 430
Найти: N4
Решение:
N6 = 430 – 320 = 110
N4 = 280 – 110 = 170
10.
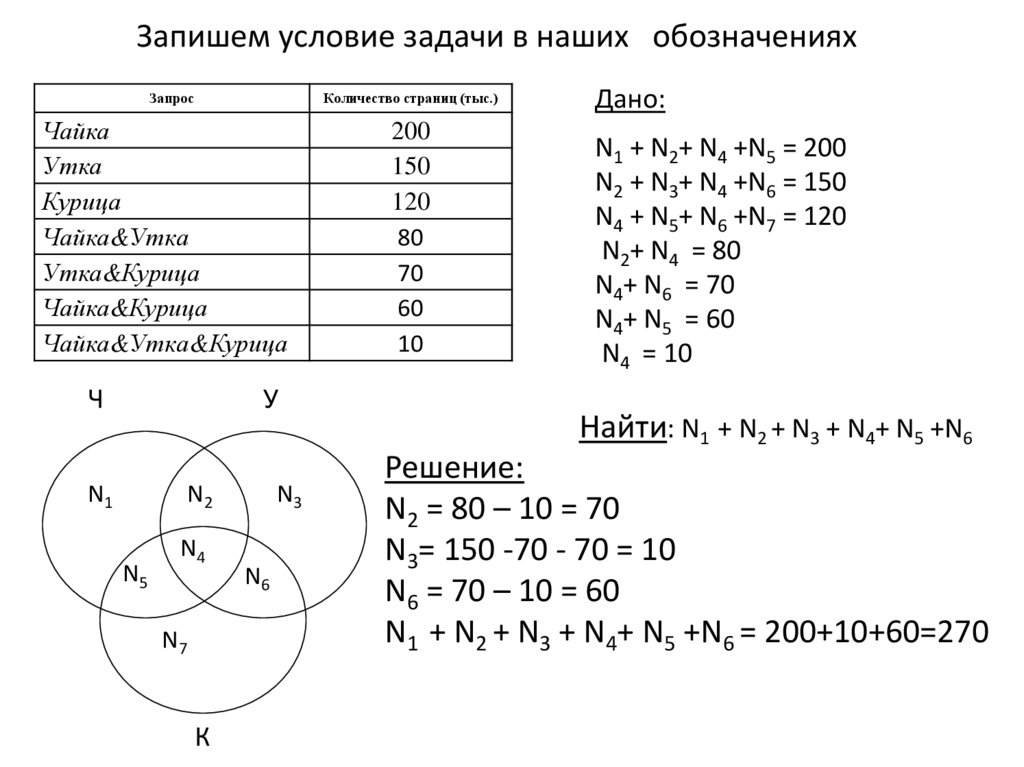
Запишем условие задачи в наших обозначенияхЗапрос
Количество страниц (тыс.)
Чайка
Утка
Курица
Чайка&Утка
Утка&Курица
Чайка&Курица
Чайка&Утка&Курица
Ч
У
N1
N2
N5
N4
N7
К
N3
N6
200
150
120
80
70
60
10
Дано:
N1 + N2+ N4 +N5 = 200
N2 + N3+ N4 +N6 = 150
N4 + N5+ N6 +N7 = 120
N2+ N4 = 80
N4+ N6 = 70
N4+ N5 = 60
N4 = 10
Найти: N1 + N2 + N3 + N4+ N5 +N6
Решение:
N2 = 80 – 10 = 70
N3= 150 -70 - 70 = 10
N6 = 70 – 10 = 60
N1 + N2 + N3 + N4+ N5 +N6 = 200+10+60=270
11.
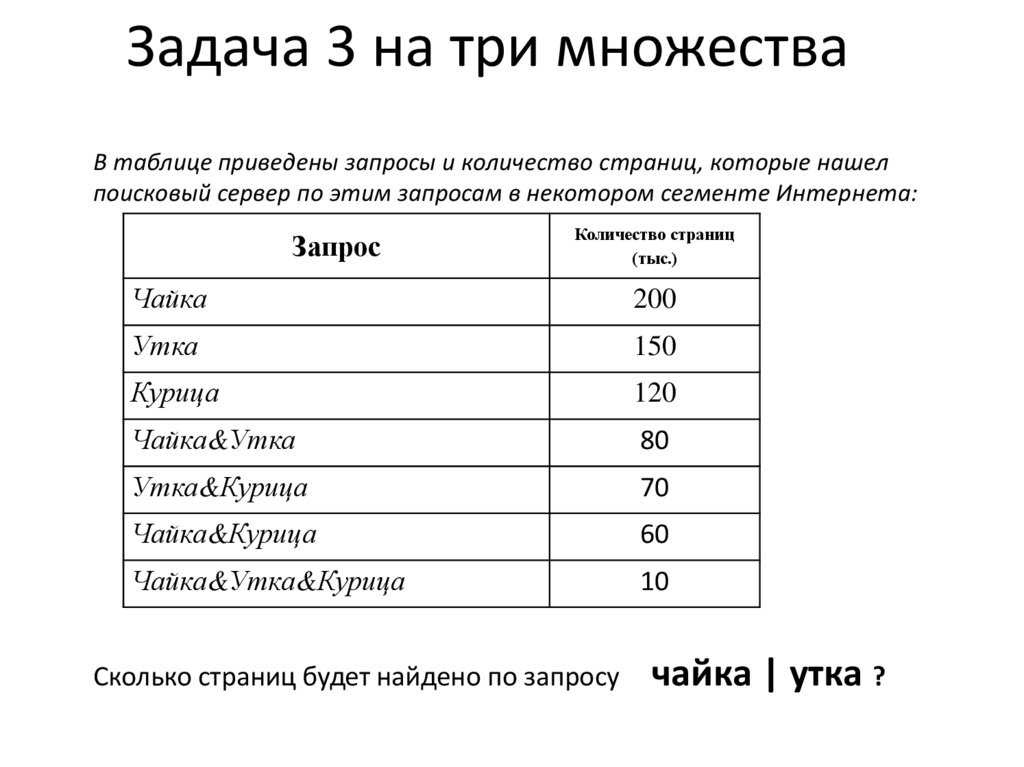
Задача 3 на три множестваВ таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте Интернета:
Запрос
Количество страниц
(тыс.)
Чайка
200
Утка
150
Курица
120
Чайка&Утка
80
Утка&Курица
70
Чайка&Курица
60
Чайка&Утка&Курица
10
Сколько страниц будет найдено по запросу
чайка | утка ?
12.
Задача 4 c пустым множествомВ таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте
Интернета:
Запрос
Количество страниц (тыс.)
Карандаш
300
Линейка
200
Ручка
280
Ручка&Линейка
80
Ручка&Карандаш
70
Линейка&Карандаш
0
Сколько страниц будет найдено по запросу
линейка | ручка | карандаш ?
13.
Запишем условие задачи в наших обозначениях, учитывая, чтомножества линейка и карандаш не пересекаются.
Запрос
Количество страниц (тыс.)
Карандаш
300
Линейка
200
Ручка
280
Ручка&Линейка
80
Ручка&Карандаш
70
Линейка&Карандаш
0
К
N1
Р
N2
N3
Л
N4
N5
Дано:
N1 + N2 = 300
N4 + N5 = 200
N2 + N3+ N4 = 280
N4 = 80
N2 = 70
Найти: N1 + N2 + N3 + N4+ N5
Решение:
N1 = 300 – 70 = 230
N5= 200 -80 = 120
N1 + N2 + N3 + N4+ N5 =
230+280+120=630
14.
Задача 5 c пустым неявным множествомВ таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте Интернета:
Запрос
Количество страниц
(тыс.)
Конверт
100
Книга
200
Журнал
400
Конверт | Книга
300
Конверт&Журнал
50
Журнал&Книга
60
Сколько страниц будет найдено по запросу:
Внимание!
Запросы: Конверт=100, Книга =
200, а запрос Конверт | Книга =
300. Это говорит о том, что
множества Конверт и Книга
не пересекаются, а значит
решение будет как в примере 4.
конверт | книга | журнал?
15.
Запишем условие задачи в наших обозначениях, учитывая,что множества Конверт и Книга не пересекаются.
Запрос
Количество страниц
(тыс.)
Конверт
Книга
Журнал
Конверт | Книга
Конверт&Журнал
Журнал&Книга
100
200
400
300
50
60
Конверт
N1
Журнал
N2
N3
N4
Книга
N5
Дано:
N1 + N2 = 100
N4 + N5 = 200
N2 + N3+ N4 = 400
N4 = 60
N2 = 50
Найти: N1 + N2 + N3 + N4+ N5
Решение:
N1 = 100 – 50 = 50
N5= 200 - 60 = 140
N1 + N2 + N3 + N4+ N5 = 50 +
400+140 = 590
16.
Задача 6 c четырьмя множествамиВ таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте Интернета:
Запрос
Количество
страниц
(тыс.)
Ростов & (Орёл & Курск | Белгород)
370
Ростов & Белгород
204
Ростов & Орёл & Курск & Белгород
68
Сколько страниц (в тысячах) будет найдено по запросу
Ростов & Орёл & Курск
17.
Заметим, что во всех четырёх запросах есть «сомножитель»«Ростов &», поэтому эта задача равносильна такой:
Запрос
Количество
страниц
(тыс.)
Орёл & Курск | Белгород
370
Белгород
204
Орёл & Курск & Белгород
68
Сколько страниц (в тысячах) будет найдено по запросу
Орёл & Курск
Поэтому решаем как пример 2 или пример 3.
18.
Запишем условие задачи в наших обозначенияхКоличество
страниц (тыс.)
Запрос
Орёл & Курск | Белгород
370
Белгород
Орёл & Курск & Белгород
204
68
О
К
N1
N2
N5
N4
N7
Б
N3
N6
Дано:
N2 + N4+ N5 +N6 + N7 = 370
N4 + N5+ N6 +N7 = 204
N4 = 68
Найти: N2 + N4
Решение:
N2 = 370 – 204 = 166
N2 + N4 = 166 + 68 = 234
19.
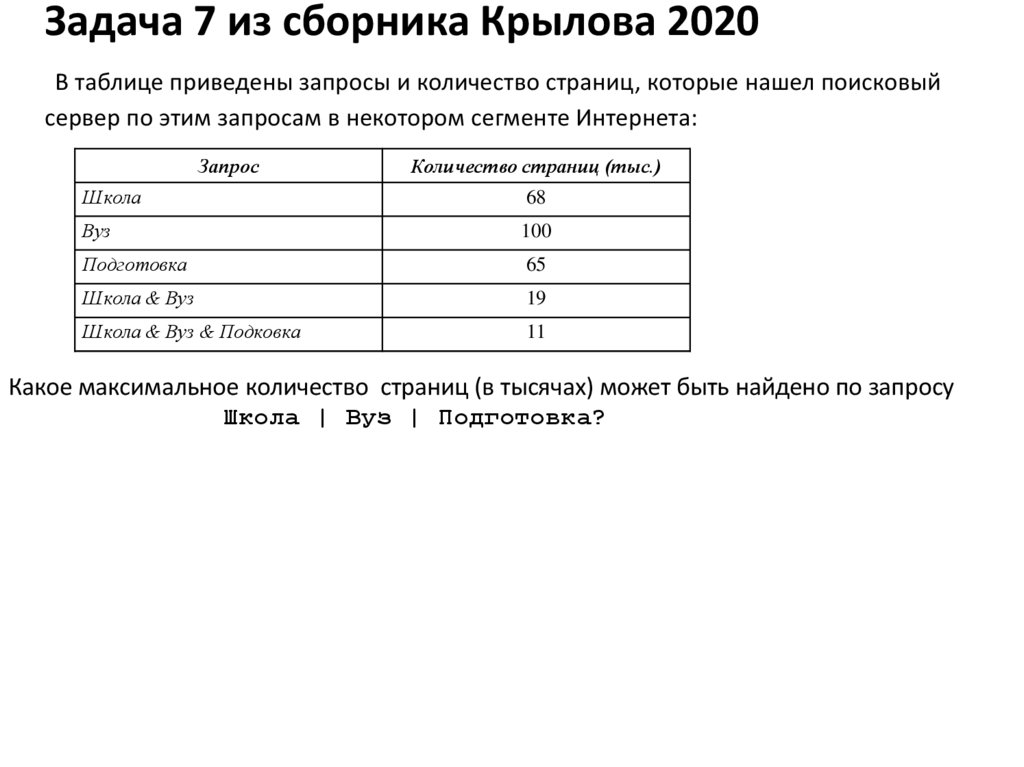
Задача 7 из сборника Крылова 2020В таблице приведены запросы и количество страниц, которые нашел поисковый
сервер по этим запросам в некотором сегменте Интернета:
Запрос
Количество страниц (тыс.)
Школа
68
Вуз
100
Подготовка
65
Школа & Вуз
19
Школа & Вуз & Подковка
11
Какое максимальное количество страниц (в тысячах) может быть найдено по запросу
Школа | Вуз | Подготовка?
20.
Запишем условие задачи в наших обозначенияхКоличество
страниц
(тыс.)
Запрос
Школа
68
Вуз
100
Подготовка
65
Школа & Вуз
19
Школа & Вуз & Подковка
11
Дано:
N1 + N2+ N4 +N5 = 68
N2 + N3+ N4 +N6 = 100
N4 + N5+ N6 +N7 = 65
N2 + N4= 19
N4 = 11
Найти: N1 +N2 + N3 + N4 + N5+ N6 +N7
В
Ш
N1
N2
N5
N4
N7
П
N3
N6
Решение:
N2 = 19 – 11 = 8
N1 + N5 = 68 - 19 = 49
N3 + N6 = 100 - 19 = 81
N1 +N2 + N3 + N4 +N5+N6=19+49+81=149
Оценим N7 из 3 уравнения. Пусть N5=0
N6=0. N7=65-11=54. тогда
N1 +N2 + N3 + N4 + N5+ N6 +N7=149+54=203
21.
ИсточникиВсе решения, составлены автором.
http://kpolyakov – сайт Полякова Ю. К.
http://www.fipi.ru – федеральный институт
педагогических изменений
http://metodist.lbz.ru/authors/informatika/3/ методические разработки Босовой Л.Л. на
официальном сайте издательства Бином













 informatics
informatics








