Similar presentations:
Система счисления
1.
2. Система счисления – это совокупность приемов и правил для обозначения и именования чисел. Знаки, используемые при записи чисел, называютс
Система счисления –это
совокупность приемов и правил для
обозначения и именования чисел.
Знаки, используемые при записи чисел,
называются цифрами.
Системы счисления
позиционные
непозиционные
3. Непозиционная система счисления – это система счисления, в которой количественные значения символов, используемых для записи чисел, не за
Непозиционная системасчисления –
это система счисления,
в которой количественные значения
символов, используемых для записи чисел,
не зависят от их положения.
4. Арифметика каменного века
Единичная (унарная)система счисления
10 - 11 тыс. лет до н. э.
любое число образуется путем
повторения одного знака,
символизирующего единицу.
5. Древнегреческая нумерация
В V веке до н.э. появилась алфавитная нумерация.Пример:
500 30 2
2 500 30
500 2 30
6. Славянская кириллическая нумерация
Пример:7. Египетская нумерация
110000
10
100
100000
1000
1000000
10000000
Пример:
= 90
5000 лет тому назад
8.
Римская система счисленияПримером непозиционной
системы счисления, которая
сохранилась до наших дней,
может служить система
счисления, применявшаяся
более двух с половиной тысяч
лет назад в Древнем Риме.
9. Римская система счисления
Пример:DC-XV=DLXXXV
Чтобы записать число, римляне использовали не
только сложение, но и вычитание.
10.
Ясачные грамотыВ старину на Руси среди простого народа широко
применялись системы счисления, отдаленно
напоминающих римскую. С их помощью сборщики
податей заполняли квитанцию об уплате подати –
ясака и делали записи в податной тетради.
- тысяча рублей,
- сто рублей,
- десять рублей,
- один рубль,
- десять копеек,
- копейка.
А чтобы не было
никаких прибавлений,
все знаки очерчивали
кругом прямыми
линиями.
Пример,1232 рубля 24
копейки изображались так:
11.
Позиционные системысчисления
Система счисления называется
позиционной, если
количественные значения
символов, используемых для
записи чисел, зависят от их
положения (места, позиции) в
записи числа
12.
Потребовалось много тысячелетий, чтобы людинаучились называть и записывать числа так, как это
делаем мы с вами. Начало этому было положено в
Древнем Египте и Вавилоне. Получив название
арабской, эта система распространилась по всей
Европе и быстро вытеснила остальные системы.
В данной системе счисления
используется десять различных
знаков (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
13.
Широкое распространения в первой трети XX векаимели элементы двенадцатеричной системы
счисления. Число 12 имеет больше делителей, чем
10 – поэтому в двенадцатеричной системе
производить расчеты удобнее, чем в десятичной. И
только возможность счета по пальцам рук склонила
чашу весов на сторону числа 10. Тем не менее,
дюжина вошла прочно в нашу жизнь: карандашей и
фломастеров в наборе 6, 12 или 24; чайные и
столовые сервизы бывают на 6 или на 12 персон;
комплект носовых платков – 12 штук.
А вот шведский король Карл XII увлекался
восьмеричной системой, считал ее более удобной
и намеревался ввести ее как
общегосударственную. Только неожиданная
смерть короля помешала осуществлению столь
необычного намерения.
14. Позиционные системы счисления
• Основная характеристика позиционной ССоснование – количество цифр,
используемое для представления чисел
• Основанием может быть любое
натуральное число.
Обозначение:
10112, 2810, 1038, ...
15. Позиционные системы счисления
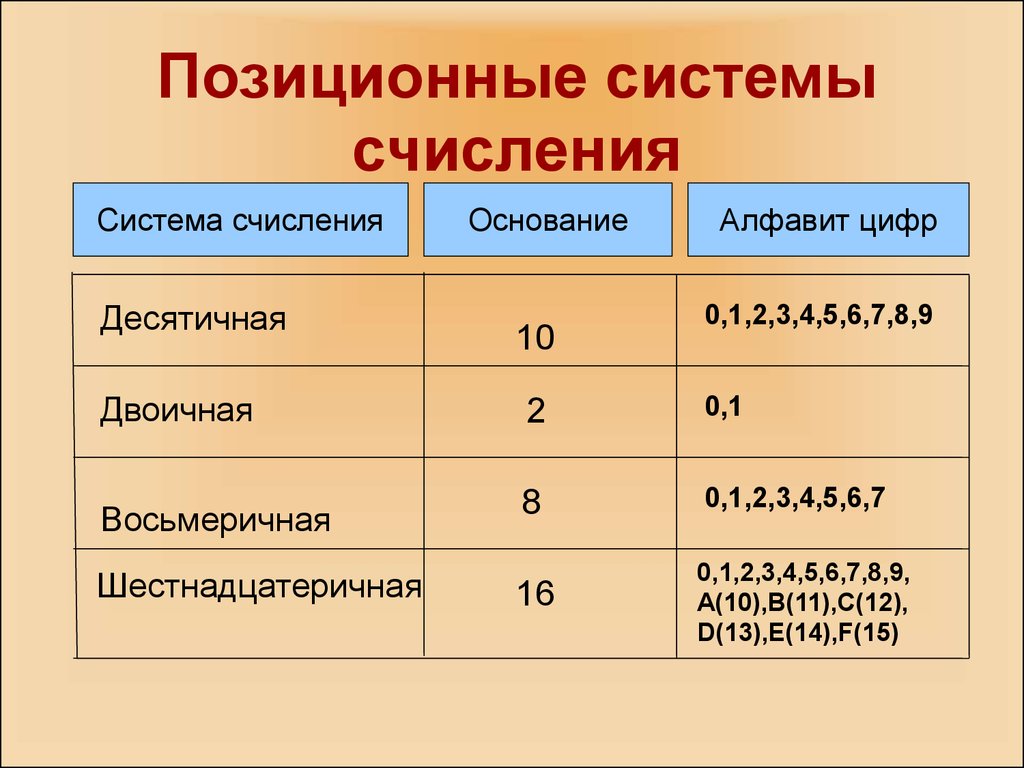
Система счисленияДесятичная
Основание
10
Алфавит цифр
0,1,2,3,4,5,6,7,8,9
Двоичная
2
0,1
Восьмеричная
8
0,1,2,3,4,5,6,7
16
0,1,2,3,4,5,6,7,8,9,
А(10),В(11),С(12),
D(13),Е(14),F(15)
Шестнадцатеричная
16.
Перевод целых чисел издесятичной системы счисления
Алгоритм перевода:
1. Последовательно выполнять деление
данного числа и получаемых неполных
частных на основание новой системы
счисления (т.е. на р) до тех пор, пока получим
неполное частное, меньше делителя;
2. Полученные остатки, являющиеся цифрами
числа в новой системе счисления, привести в
соответствие с алфавитом новой системы
счисления;
Пример: 1710
Х2
17 2
1
8
0
2
4
0
3. Составить число в новой системе
счисления, записывая его, начиная с
последнего частного и все полученные
остатки в обратном порядке.
2
2
0
Ответ: 1710
2
1
100012
17. Сложение 0+0=0 0+1=1 1+0=1 1+1=10
Арифметика с двоичнымичислами
1. Сложение
0+0=0
0+1=1
1+0=1
1+1=10
2. Вычитание
0-0=0
0-1=11
1-0=1
1-1=0
3. Умножение
0•0=0
1•0=0
0•1=0
1•1=1
















 informatics
informatics








