Методы минимизации функции многих переменных. Лекция 10

1. Методы минимизации функции многих переменных

2. Классификация методов

3. Покоординатные методы

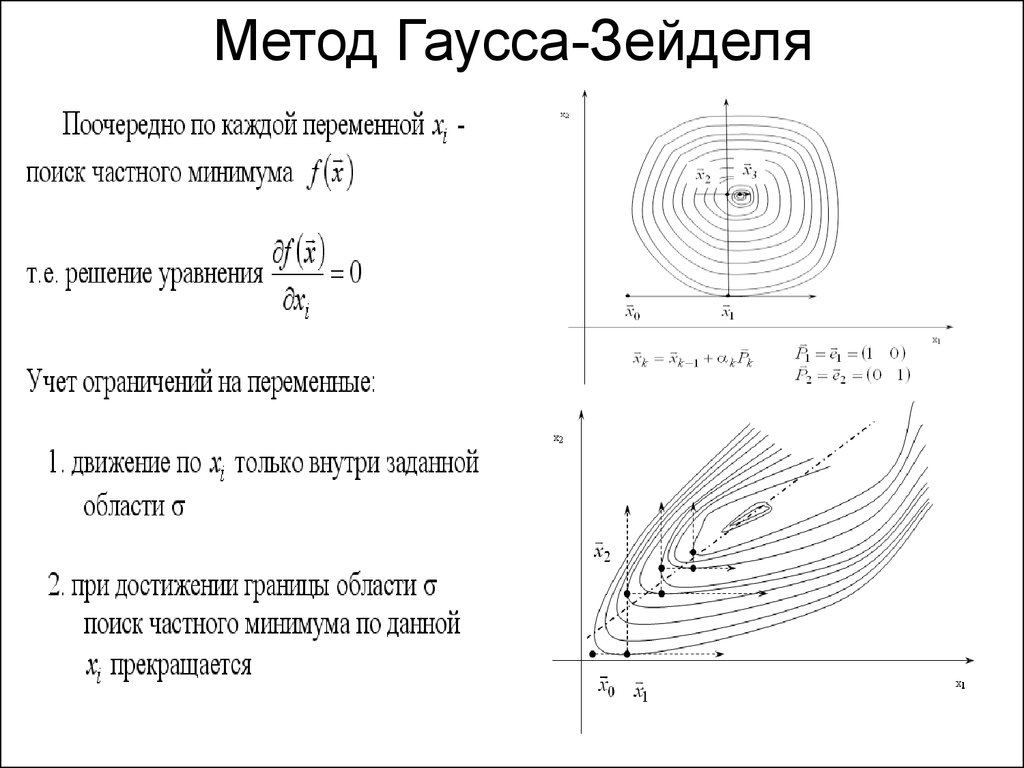
4. Метод Гаусса-Зейделя

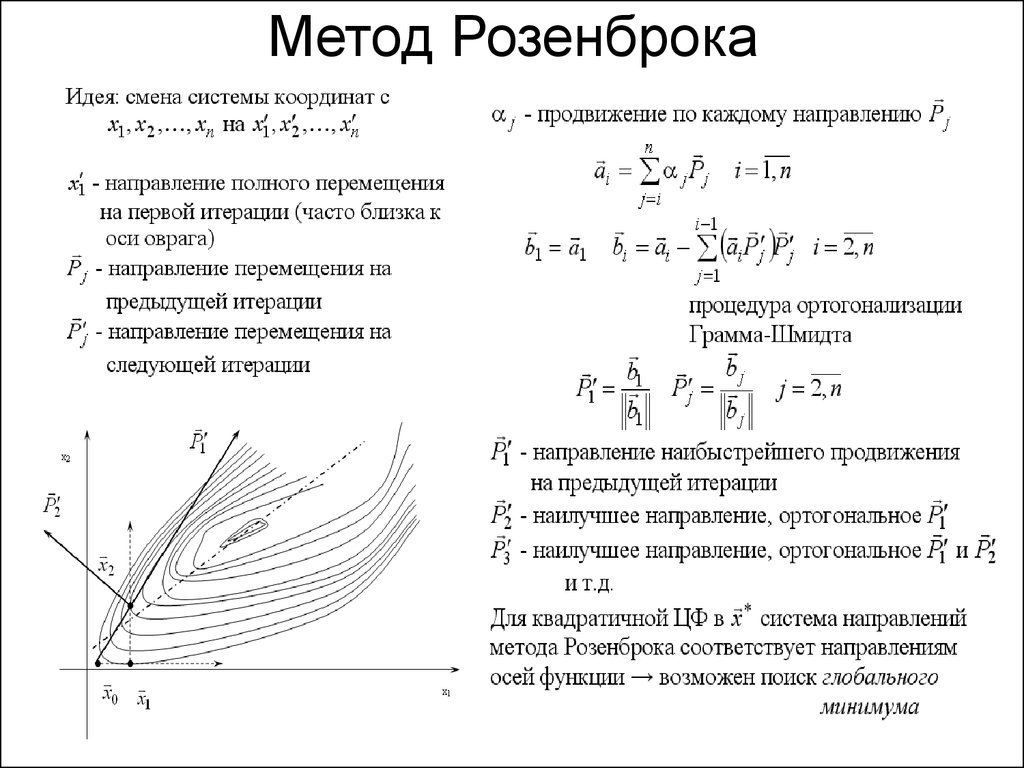
5. Метод Розенброка

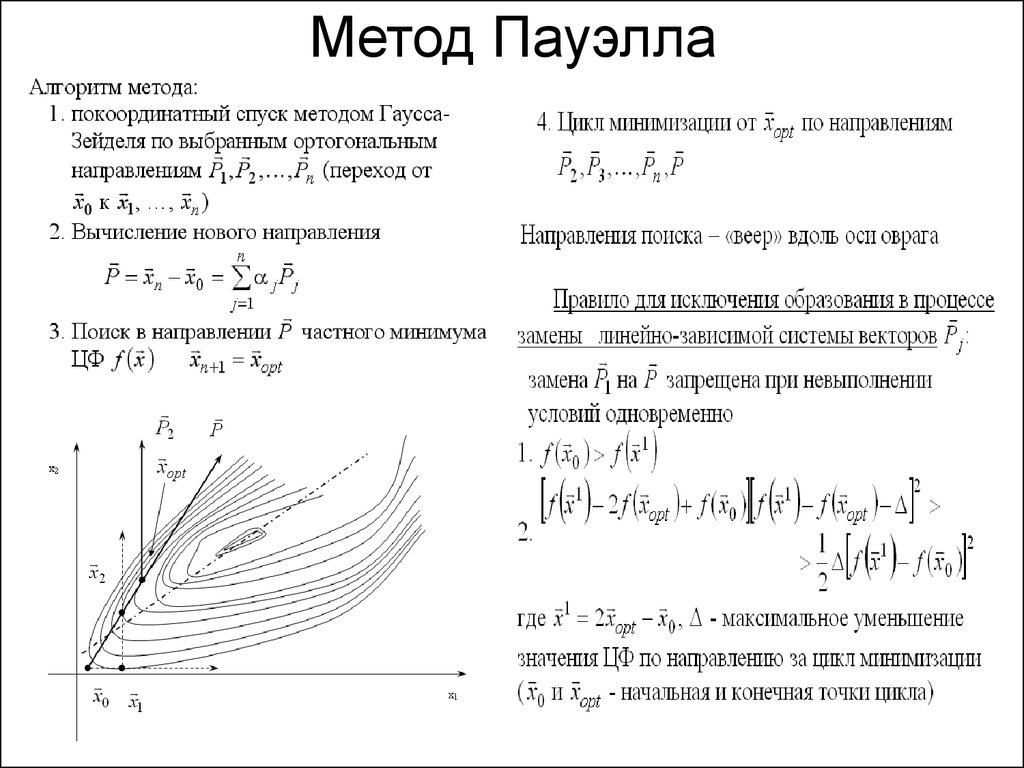
6. Метод Пауэлла

7. Симплексный метод Нельдера-Мида

8. Симплексный метод Нельдера-Мида

9. Симплексный метод Нельдера-Мида

10. Градиентные методы

• Идея: выбор
«наилучшего»
направления спуска
• Градиент –
направление
наискорейшего
возрастания ЦФ
• Антиградиент –
«наилучшее»
направление к точке
минимума
• Градиентные
методы
• 1. Метод
наискорейшего
спуска
• 2. Метод
сопряженных
градиентов
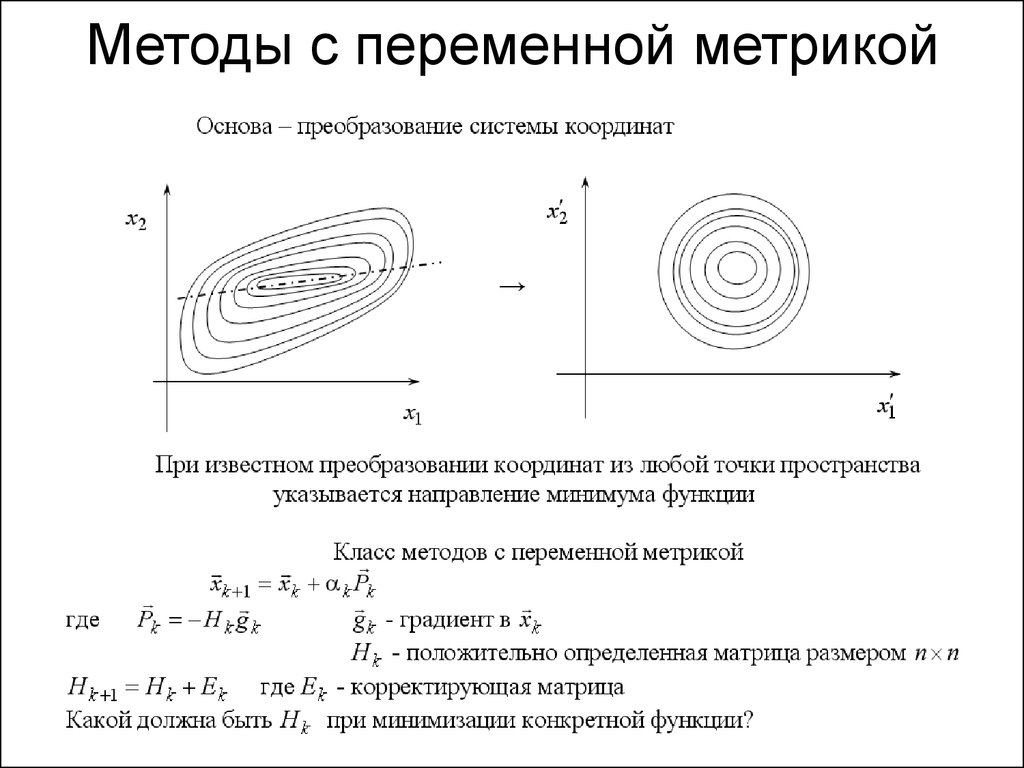
• 3. Семейство
методов с
переменной
метрикой
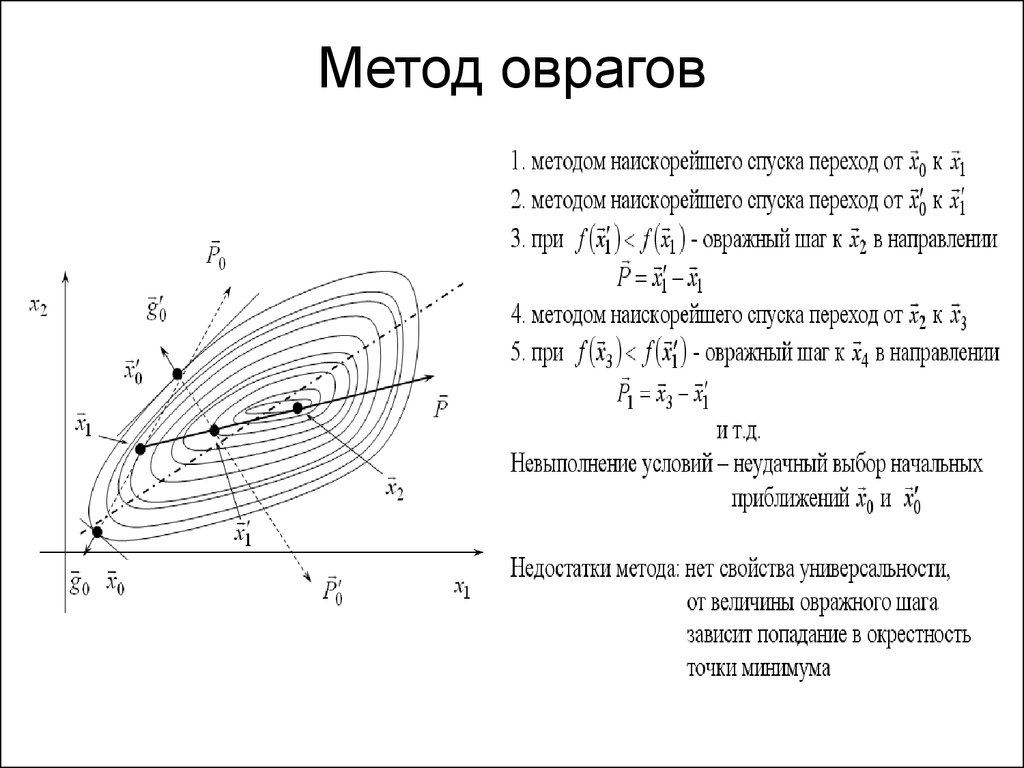
• 4. Метод оврагов

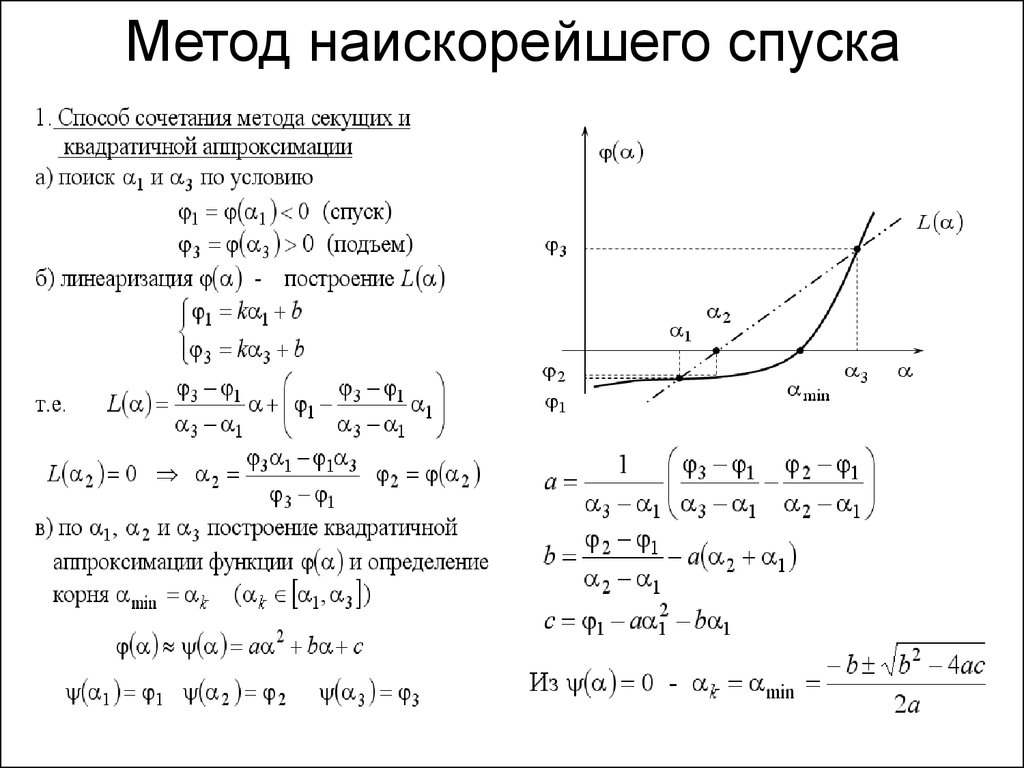
11. Метод наискорейшего спуска

12. Метод наискорейшего спуска

13. Метод наискорейшего спуска

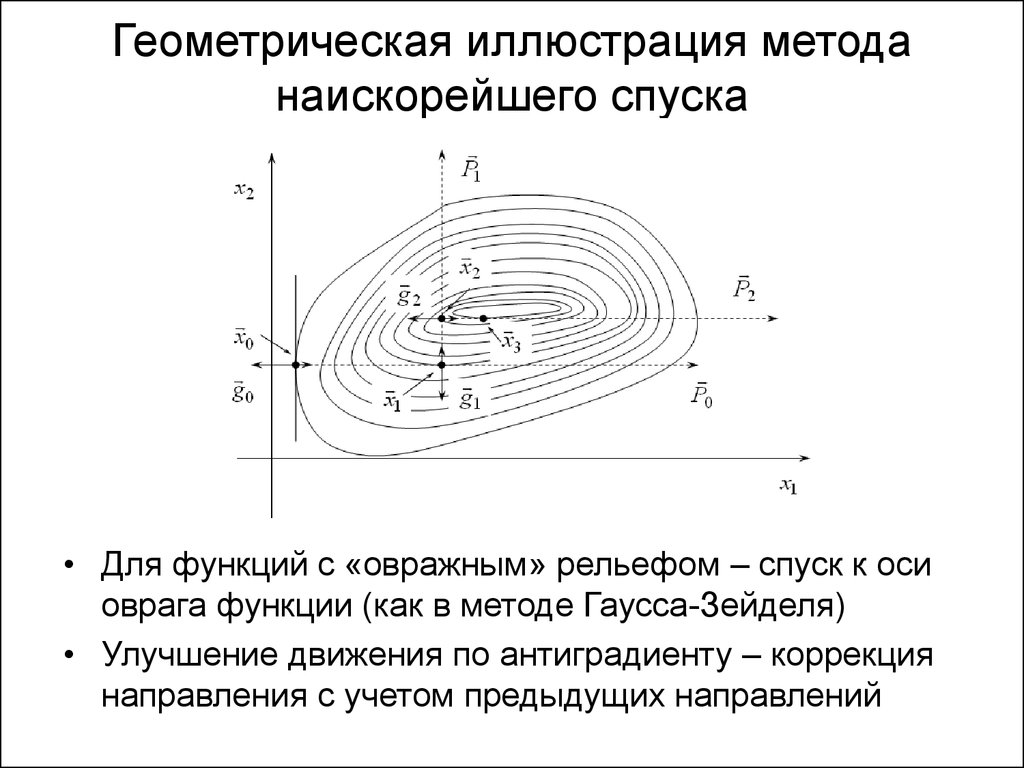
14. Геометрическая иллюстрация метода наискорейшего спуска

• Для функций с «овражным» рельефом – спуск к оси
оврага функции (как в методе Гаусса-Зейделя)
• Улучшение движения по антиградиенту – коррекция
направления с учетом предыдущих направлений

15. Метод сопряженных градиентов

16. Методы с переменной метрикой

17. Методы с переменной метрикой

18. Методы с переменной метрикой

19. Методы с переменной метрикой

20. Метод оврагов

21. Методы второго порядка

22. Сравнение методов