Соединения конденсаторов

1.

Решение задач
«Соединения конденсаторов»
10 класс
Смирнова С.Г.
учитель физики
МОУ «Луховский лицей»

2.

3.

4.

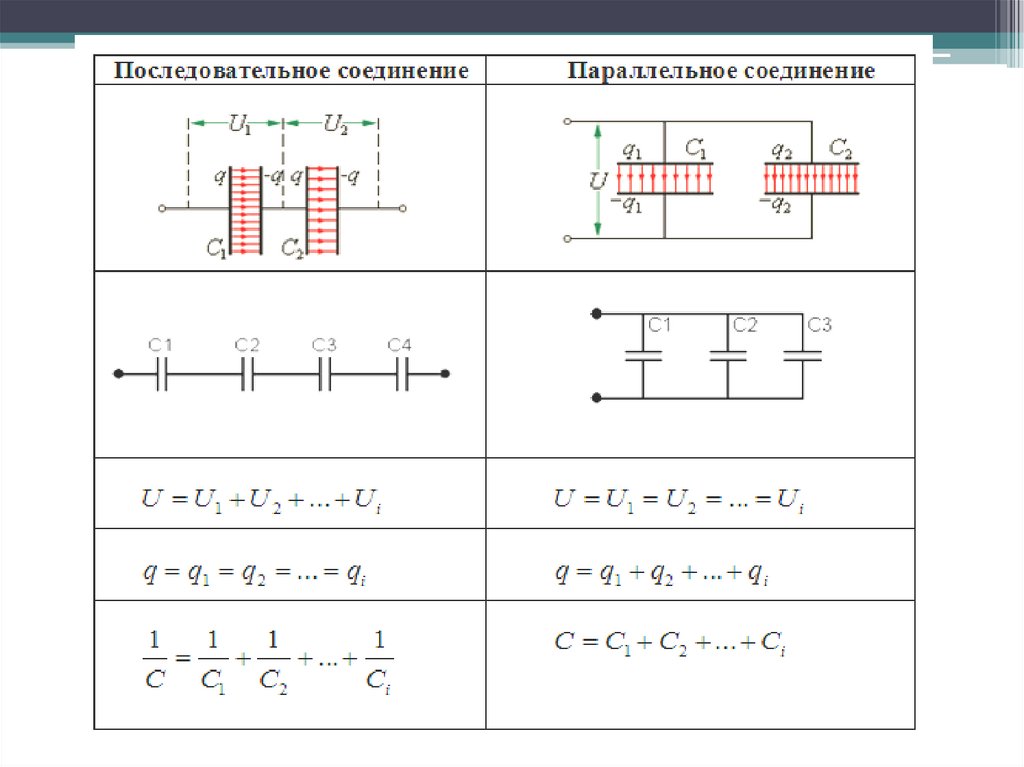
Примеры решения задач
Соединение конденсаторов
Алгоритм решения задач
1) Делаем рисунок.
2) Определяем последовательно и параллельно соединенные
конденсаторы. Напоминаем, что признаком последовательного
соединения является равенство заряда, а параллельного одинаковая
разность потенциалов.
3) Если соединения неочевидны, то находим точки схемы, потенциалы
которых равны.
4) Соединяем эти точки или не учитываем наличие конденсатора,
присоединенного к этим точкам, т.к. он не накапливает электрический
заряд.
5) Рисуем эквивалентную схему, которую используем для расчета Сэкв.

5.

Задача 1. Четыре конденсатора электроемкостями С1 = 1 мкФ,
С2 = 1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано
на рисунке. К точкам А и В подводится напряжение U = 140 В.
Найдите заряд и напряжение на каждом из конденсаторов.
Решение.
С2,3 С2 С3
1
1
1
1
Cэкв С1 С2,3 С4
q1 q2,3 q4 CэквU
1
Cэкв
Сэкв
1
1
1 1
7 1
6
6
6
6
1
10
1
3
10
2
10
Ф
4
10
Ф
4 / 7 10 6 Ф
q1 q2,3 q4
4 / 5 10 6 140 Кл
8 10 5 Кл

6.

q1 8 10 5
U1
В 80 В
6
C1 1 10
q4 8 10 5
q4 8 10 Кл, U 4
В = 40 В
6
C4 2 10
5
U 2 U3
q2,3
C2,3
8 10 5
В = 20В
6
4 10
q2 C2U 2 1 10 6 20Кл 2 10 5 Кл
q3 C3U 3 3 10 6 20 Кл 6 10 5 Кл

7.

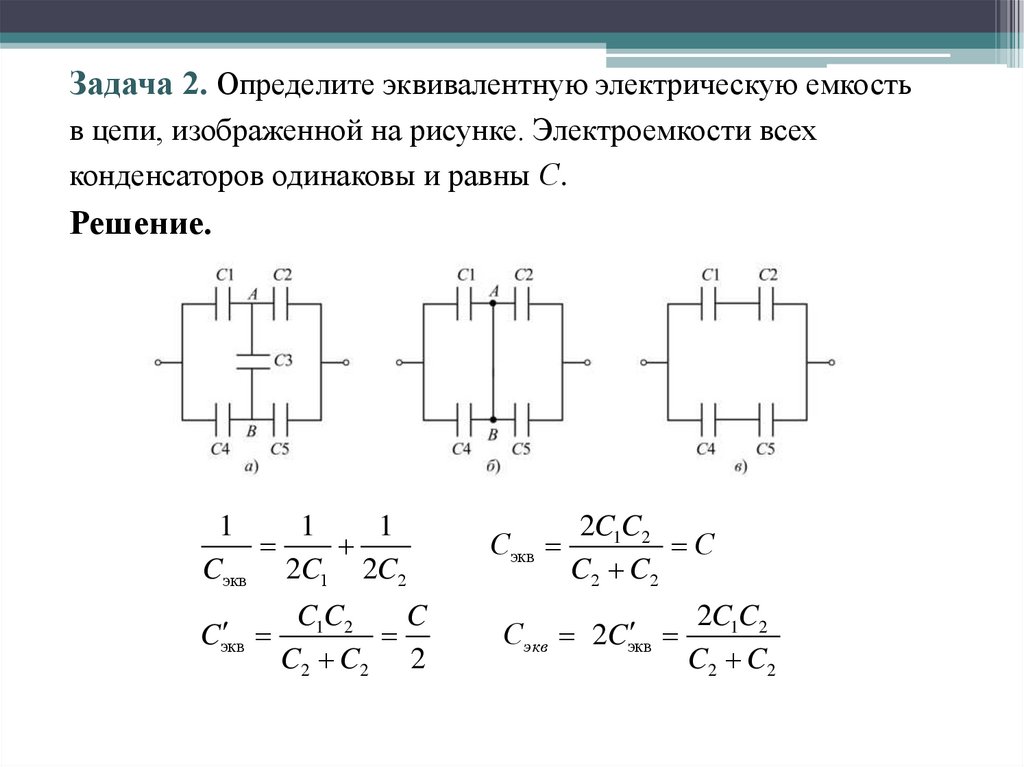
Задача 2. Определите эквивалентную электрическую емкость
в цепи, изображенной на рисунке. Электроемкости всех
конденсаторов одинаковы и равны С.
Решение.
1
1
1
Cэкв 2C1 2C2
Cэкв
C1C2
C
C2 C2 2
Сэкв
Сэкв
2C1C2
C
C2 C2
2Cэкв
2C1C2
C2 C2

8.

Задача 3. Определите электроемкость системы конденсаторов,
изображенной на рисунке, если разность потенциалов подводится
к точкам а) A, D; б) В, D.
Решение.
а) B = E
С С
Сэкв1 С 2С
2 2
б) А = E
Сэкв2 = 2С

9.

Задача 4. Определите емкость системы, изображенной на
рисунке, если C1 = С2 = С3 = С4 = С5 = С6 = С7 = С.
Решение.
С6,7 2 С
1
C5,6,7
1
1
1
1
3
2
С5,6,7 С
C6,7 C 2С С 2С
3
С4 – С7 :
С
5
С4,5,6,7 2 С С
3
3
Сэкв 13 / 21 С

10.

Задача 5. Конденсатор электроемкостью С1 = 1 мкФ,
заряженный до разности потенциалов U1 = 100 В и отключенный
от источника, соединили параллельно с конденсатором
электроемкостью С2 = 3 мкФ, заряженным до разности
потенциалов U2 = 60 В. Определите заряд каждого
из конденсаторов и разность потенциалов между обкладками
после их соединения, если
1) соединяются обкладки, имеющие одноименные заряды;
2) соединяются обкладки, имеющие разноименные заряды.
Решение.
1) Сэкв С1 С2 , q q1 q2 C1U1 C2U 2
С1U1 C2U 2
q
U 0
70 В
Cэкв
Cэкв
q1 С1U '0 7 10 5 Кл
q2 С2U '0 21 10 5 Кл

11.

q q1 – q2 C1U1 – C2U 2
U 0
C1U1 C2U 2
C1 C2
20В
5
q1 С1U 0 2 10 Кл
5
q2 C2U 0 6 10 Кл

12.

Задача 6. Энергия плоского воздушного конденсатора
W1 = 2 10-7 Дж. Определите энергию конденсатора после
заполнения его диэлектриком с диэлектрической
проницаемостью = 2, если:
1) конденсатор отключен от источника питания;
2) конденсатор подключен к источнику питания.
Решение.
q02
1) W2
2C2
ε 0 εS
0 S
C2 =
C1 C1
d
d
q02
W
W2
10 7 Дж
2 C1
C2U 02
2) W2
С2 С1
2
C1U 02
W2
W1 4 10 7 Дж
2

13.

Задача 7. Пластины плоского конденсатора подключены
к источнику U = 2 В. Определите изменение емкости и энергии
электрического поля конденсатора, если конденсатор
наполовину заполнен диэлектриком с диэлектрической
проницаемостью = 2. Расстояние между пластинами d = 1 см,
площадь пластин S = 50 см2.
Решение.
ε0 S ε0 S
εε S
C1 =
=
C2 = 0
d
2d
2d
ε S
C = C1 +C2 = 0 ( ε + 1 )
2d
S
S S
С С – С0 0 1 0 0 1 2, 21 10 12 Ф
2d
d
2d
CU 2 C0U 2 ΔCU 2
W =
2
2
2
2
0 S 1 U
W
8,85 10 12 Дж
2d
2
2

14.

Задача 8. В плоский воздушный конденсатор вставляется металлическая
пластина толщиной d0. Заряд на обкладках конденсатора q. Конденсатор
отключен от источника. Расстояние между пластинами d, площадь
пластин S. Определите изменение электроемкости конденсатора и энергии
его электрического поля, если конденсатор не подключен к источнику.
Решение.
0 S
0 S
C1
, С2
l1
l2
l
l
l l
1
1
1
1 2 1 2
Cэкв С1 С2 ε 0 S ε 0 S
ε0 S
l1 l2 d – d 0 , Cэкв
С Сэкв – С0
0 S
d d0
ε0 S
ε S
ε 0 Sd 0
0
0
d d0
d
d d0 d
q2
q2
q 2 d d0
d q 2 d0
W
0
2Cэкв 2C0 2 0 S
0 S 2 0 S

15.

Задача 9. Определите изменение заряда проводящей сферы
радиуса 10 см, первоначально заряженной до потенциала 104 В,
если с течением времени она частично потеряла заряд и ее энергия
уменьшилась на 1,5 10-4 Дж.
Решение.
C 2
Wэ
С 4πε 0 εr
2
C
ΔWэ = Wэ2 – Wэ1 = ( φ 22 – φ12 )
2
2 Wэ
Wэ
2
12
φ12
C
2πε 0 εr
Wэ
2
q C ( 2 1 ) 4 0 r
1 1 1, 67 10 8 Кл
2πε 0 r