Similar presentations:
Программирование в MathCAD
1. Программирование в MathCAD
ПРОГРАММИРОВАНИЕMATHCAD
В
2.
Программирование в MathCADбезмодульное
программирование
модульное
программирование
реализуется записью
соответствующих конструкций
непосредственно в
математических областях
документа MathCAD.
Используется для сравнительно
простых алгоритмов
реализуется в виде отдельных
независимых алгоритмов
вычисления, представляющих
собой отдельные программные
модули (подпрограммы функции (П-Ф))
3.
Безмодульное программированиев MathCAD
Программирование линейных алгоритмов
Особенность: строго последовательное выполнение всех операций
алгоритма без пропусков и повторений вычислений.
Составить программу для вычисления корней квадратного уравнения
b 5
a 2
c 8
2
d b 4 a c
x1
b d
2 a
x1 1.25 1.561i
Проверка найденных корней:
2
a x1 b x1 c 0
x2
b d
2 a
x2 1.25 1.561i
2
a x2 b x2 c 0
4.
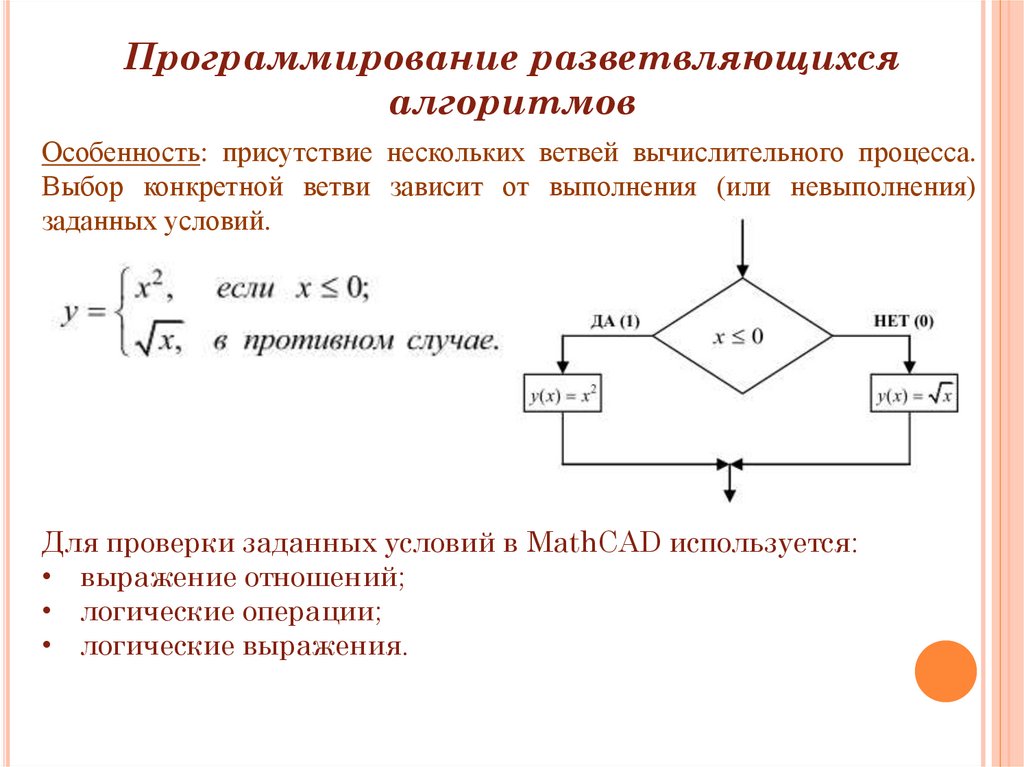
Программирование разветвляющихсяалгоритмов
Особенность: присутствие нескольких ветвей вычислительного процесса.
Выбор конкретной ветви зависит от выполнения (или невыполнения)
заданных условий.
Для проверки заданных условий в MathCAD используется:
• выражение отношений;
• логические операции;
• логические выражения.
5.
Программирование разветвляющихсяалгоритмов
Выражением отношений (или просто отношением)
называется конструкция вида:
<выр.1> <операция отношения> <выр.2>
где <выр.1>, <выр.2> – произвольные арифметические выражения,
<операция отношения> – любая из следующих операций:
<│≤│>│≥│=│≠
6.
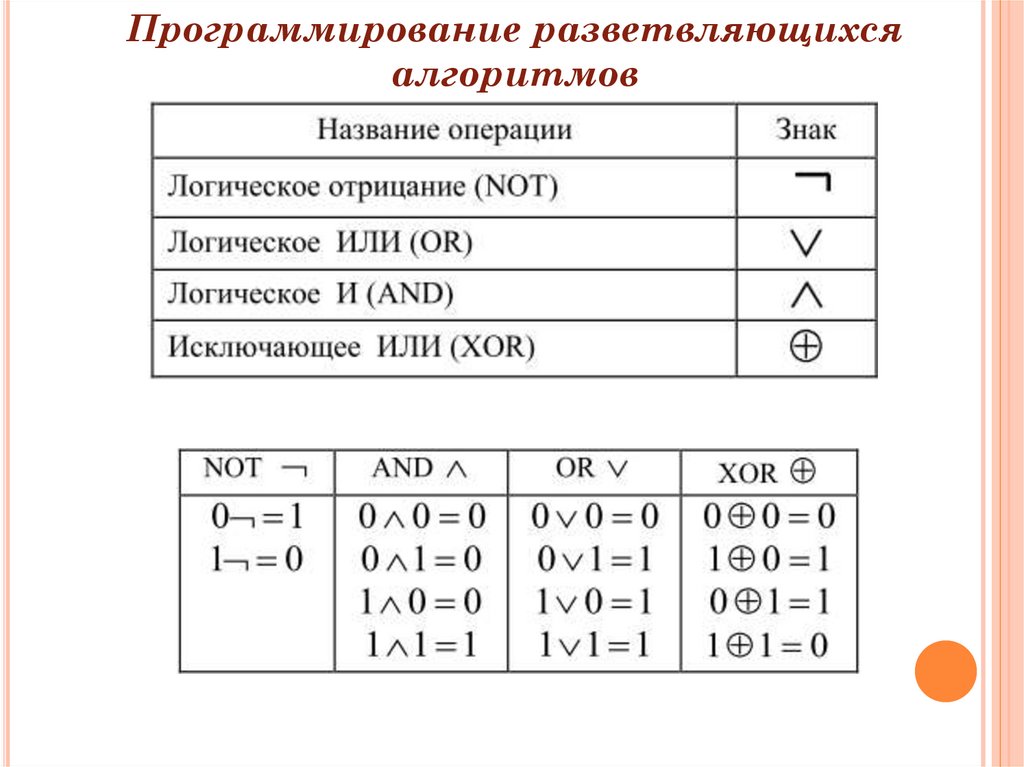
Программирование разветвляющихсяалгоритмов
7.
Программирование разветвляющихсяалгоритмов
Логическое выражение – конструкция, состоящая из
выражений отношений, логических операций и круглых скобок.
Принимает значения: 1 или 0.
Вычисляется слева направо с учетом приоритета входящих в
выражение операций:
• круглые скобки;
• логическая операция И (AND);
• логические операции ИЛИ (OR) и исключающая ИЛИ (XOR);
• выражения отношений.
x 0.2
y 0.8
( 0.5 x 0.5) ( 1 y 1) 1
f ( x y) ( 0.5 x 0.5) ( 1 y 1)
f ( 1 0.3) 0
8.
Условная функция ifif (<логическое выражение>, <выр. 1>, <выр. 2>)
где имя функции if вводится с клавиатуры.
y( x) if x 0 ln( x) e
y( 3) 0.05
x
y( 2.71) 0.997
9.
Вложенная условная функция if1
1 3 1 4
y( x) if x 1 x if x 0 x x
2
3
4
y( 2) 0.707
y( 0.5) 0.265
y( 2) 0.297
10.
Запрограммировать алгоритм, вычисляющий величину x, последующему правилу: если x < 2, то значение x оставить без
изменения, в противном случае величину x увеличить на 2.
y( x) if ( x 2 x 2 x)
y( 6) 8
y( 1) 1
11.
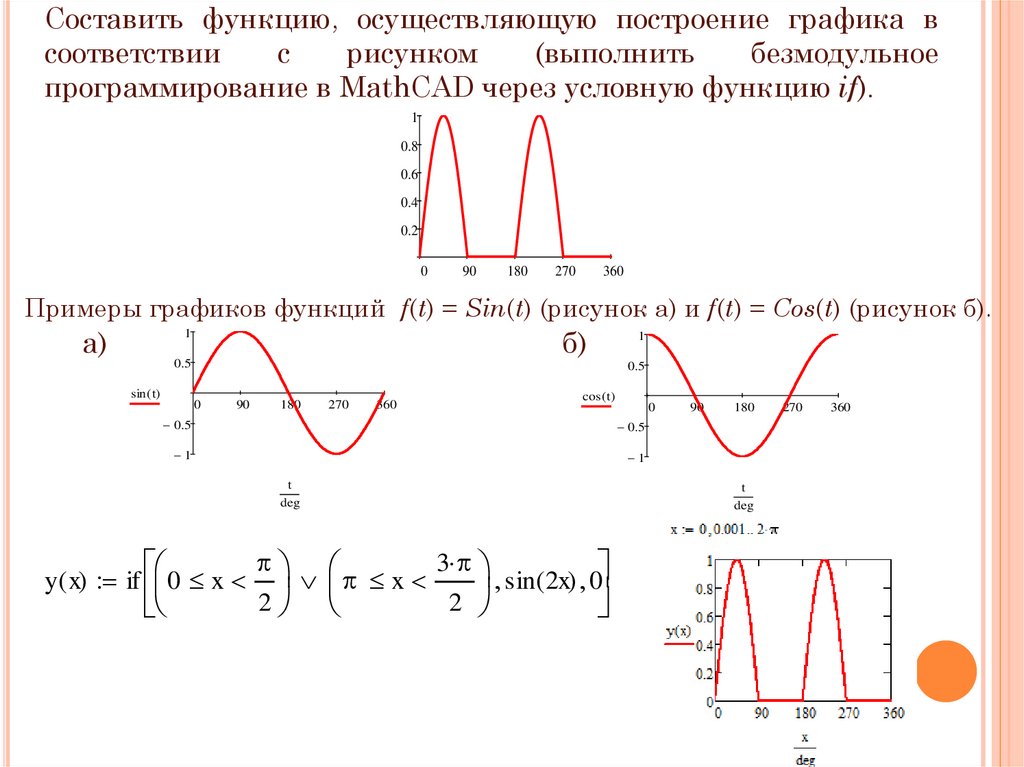
Составить функцию, осуществляющую построение графика всоответствии
с
рисунком
(выполнить
безмодульное
программирование в MathCAD через условную функцию if).
1
0.8
0.6
0.4
0.2
0
90
180
270
360
Примеры графиков функций f(t) = Sin(t) (рисунок а) и f(t) = Cos(t) (рисунок б).
а)
б)
1
0.5
sin ( t)
1
0.5
0
90
180
270
cos ( t)
360
0
0.5
0.5
1
1
t
deg
y( x) if 0 x
2
90
180
t
deg
x
3
sin( 2x) 0
2
270
360
12.
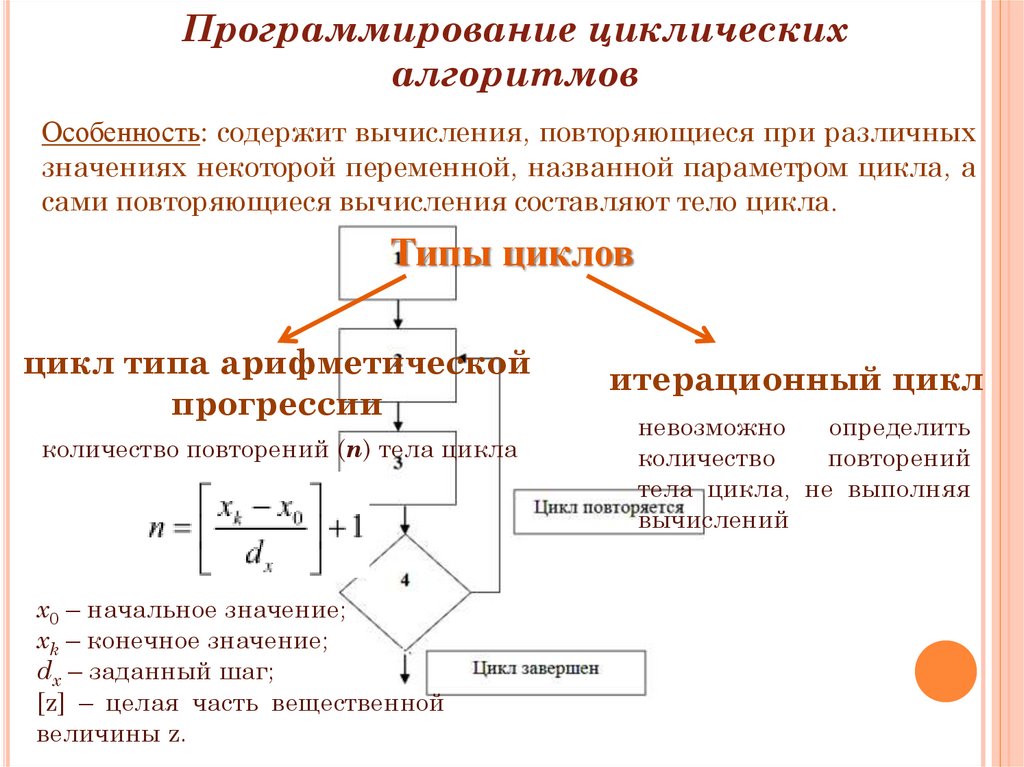
Программирование циклическихалгоритмов
Особенность: содержит вычисления, повторяющиеся при различных
значениях некоторой переменной, названной параметром цикла, а
сами повторяющиеся вычисления составляют тело цикла.
Типы циклов
цикл типа арифметической
прогрессии
количество повторений (n) тела цикла
x0 – начальное значение;
xk – конечное значение;
dx – заданный шаг;
[z] – целая часть вещественной
величины z.
итерационный цикл
невозможно
определить
количество
повторений
тела цикла, не выполняя
вычислений
13.
Цикл типа арифметической прогрессииВычислить значения функции
и построить график этой функции для всех x, изменяющихся в интервале
[–0.5, 2.5] с шагом ∆x = 0.1; a, b – заданные вещественные числа.
a 2
y( x)
ln x
2
a b
b 4
x 0.5 0.4 2.5
2
0.5
0
y ( x)
0.5
1
1.5
2
1
0
1
x
2
3
14.
y ( x)0.5
1
Цикл типа арифметической прогрессии
Сформировать матрицу (двумерный массив) В1.5
по следующему
правилу:
2
1
0
ORIGIN 1
n 3
m 6
i 1 n
j 1 m
1
Bi j
i j 1
0.333 0.25 0.2 0.167 0.143 0.125
B 0.25
0.2 0.167 0.143 0.125 0.111
0.2 0.167 0.143 0.125 0.111 0.1
1
x
2
15.
Итерационный циклРешить методом Ньютона
1.2. Решение методом Ньютона
2
f ( x) 5 sin( x) 4 x 5.8
n 100
100
i 1 n
df ( x)
d
4
10
f ( x)
dx
x0 3
df ( x) ( 5 cos ( 3) 24 )
10 5
0
5
10
100 приближения по формуле Ньютона
Вычисление первого
f ( t)
200
f x0
300
x1 1.981
x1 x0
df x0
400
f xi
xi 1 until xi xi 1 xi
df
x
t
i
T
определение числа итераций за которые итерационны
x ( 3 1.9811938 1.6833021 1.6429796 1.6421985 1.6421982 )
Определение
числа итераций,
заитераций
которые итерационный
процесс
определение
числа
итераций
которыеитерационный
итерационный
определение
числа
зазакоторые
п
сошелся:
j last ( x)
j 5











 programming
programming








