Дискретная математика

1.

Дискретная математика
2020\2021 учебный год
весенний семестр
Учебные группы: 589-1, 589-2, 589-3
1

2.

Дискретная математика - часть математики,
которая зародилась в глубокой древности.
Главной её спецификой является
дискретность,
( антипод непрерывности).
2

3.

Дискретность (от лат. discretus - разделённый,
прерывистый) , прерывность; противопоставляется
непрерывности. Например, дискретное изменение
какой-либо величины во времени - это изменение,
происходящее
через
определённые
промежутки
времени (скачками) ; система целых чисел (в
противоположность системе действительных чисел)
является дискретной (см. Непрерывная функция) .
В физике и химии дискретность означает зернистость
строения материи, её атомистичность.
3

4. Цели и задачи дисциплины

Разделы дискретной математики
4

5.

В широком смысле дискретная
математика включает в себя такие
сложившиеся разделы математики, как
теория чисел,
алгебра,
математическая логика
и ряд разделов, которые наиболее
интенсивно стали развиваться в середине
20-го века в связи с внедрением ЭВМ
(например, «теория графов»).
5

6.

Математическая логика
Математическая кибернетика
Теория функциональных систем
Общая алгебра
Комбинаторика (отдельные разделы)*
Комбинаторная логика
Сортировки
Теория графов
Машинная арифметика
Теория алгоритмов
Теория игр
… … … …?
6

7.

Теория автоматов
Теория множеств (отдельные разделы)
Теория чисел (отдельные разделы)
Теория формальных грамматик
Теория булевых функций
Логическое программирование
Функциональное программирование
Булева алгебра
Комбинационная логика
Асинхронная логика
Математическая лингвистика
Теория искусственного интеллекта
Теория расписаний
7

8. Обобщая определение и роль дискретной математики можно сказать :

ЛК1
с.2
8

9.

Дискретная математика совокупность математических
дисциплин, изучающих свойства
абстрактных дискретных
объектов, т.е. свойства
математических моделей объектов,
процессов, зависимостей,
существующих в реальном мире,
которыми оперируют в различных
областях знаний.
9

10.

Дисциплины направлений подготовки
бакалавров на кафедре КСУП ФВС, в
которых используются
методы и задачи дискретной математики.
10

11.

230100.62
Сети и телекоммуникации
Дискретная математика
11

12.

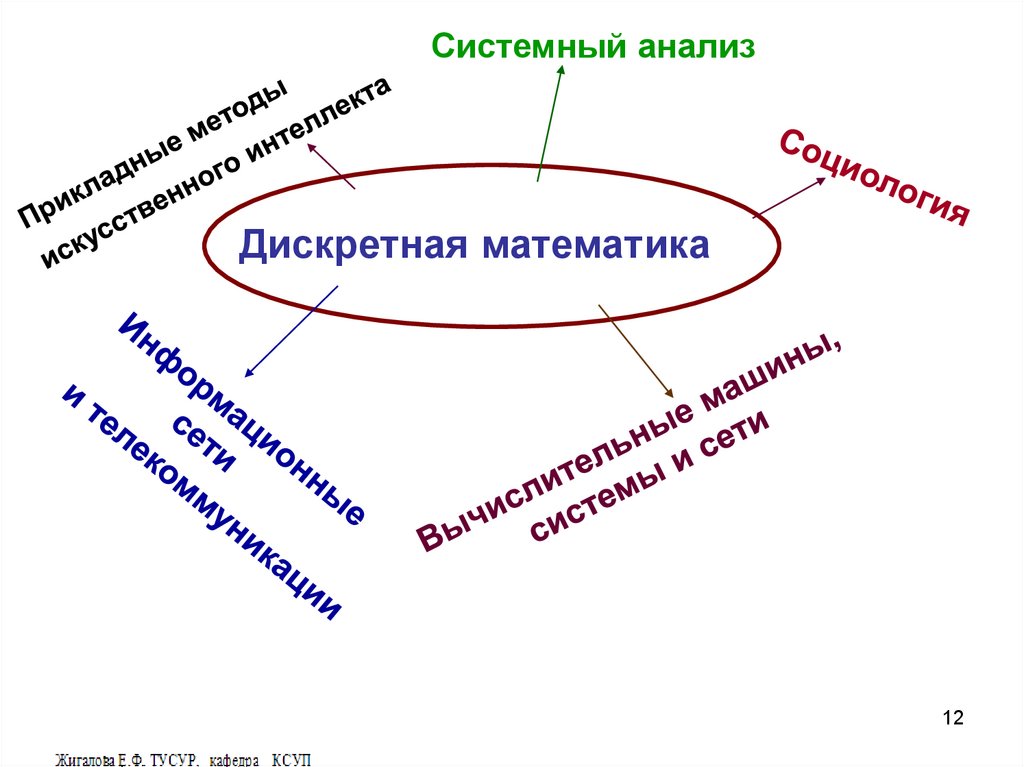
220400.62
Системный анализ
Дискретная математика
12

13.

Разделы дискретной математики, для
изучения в весеннем семестре
13

14.

I.
Теория множеств
II. Теория графов.
III. Переключательные функции
IV. Комбинатрика
14

15.

Дискретная математика сегодня
является не только фундаментом
математической кибернетики, но и
важным звеном математического
образования.
Главная задача курса - это
обучение методам и мышлению,
характерным для дискретной
математики.
15

16.

Лабораторные занятия
16

17. Методические указания к выполнению лабораторных работ

В ходе выполнения лабораторной работы
необходимо изучить теоретический материал по
данной теме, изложенный в учебном пособии и
лекциях.
Для своего варианта (выдается
преподавателем) выполнить индивидуальное
задание по каждой теме лабораторной работы.
Оформить отчет по выполненной лабораторной
работе.
Сдать отчет преподавателю и защитить
результаты выполненной работы.
17

18. Требования к оформлению отчетов по лабораторным работам

1. Отчет оформлять в текстовом редакторе WORD с
обязательным приложением титульного листа,
оформленным в соответствии с требованиями ГОС-а.
• На титульном листе необходимо указать:
— № лабораторной работы,
— № варианта индивидуального задания;
— название темы данной лабораторной работы;
— Ф.И.О. студента, выполнившего данную работу;
— № группы;
— дата сдачи отчёта.
18

19. Оценка качества защиты лабораторных работ в рейтинговых единицах

19

20.

Рейтинг отчётов по лабораторным работам
Точность
определе
-ний
Чёткость
содержательной
постанов
ки задачи
Чёткость
формальной
постанов
ки задачи
Знание
метода,
алгоритма
решения
задачи
Оформле
-ние
Отчёта
( по
требован
иям)
Умение
интерпре
-тировать
данные
Умение
анализировать
полученные
результаты
Творческая
активность
Своевреме
нность
сдачи
отчёта
1
2
3
4
5
6
7
8
9
4
4
5
2-5
3
4
5
8
2
max ∑ = 25 + 9 + 6 = 40 [БАЛЛОВ]
Оценки:
«отлично» — 34- 40
«хорошо» — 30 - 33
«удовлетворительно» — 25 - 29
«неудовлетворительно» < 25
20

21. Дополнительная информация к рейтингу

• Допуск к зачёту/экзамену студент получает
при условии выполнения всех лабораторных и контрольных
работ.
• Получение зачёта «автоматом» :
при условии выполнения всех лабораторных и контрольных
работ с оценкой «хорошо» или «отлично» в срок.
• Если нет допуска к зачёту, то :
для допуска необходимо выполнить все виды учебных
работ по данной дисциплине и написать реферат по какойлибо теме (названной преподавателем) из рабочей
программы.
21

22.

Учебно-методическая литература
22

23.

Основная
1. Хаггарти,Род. Дискретная математика для программистов. Пер. С
английского: Учебное пособие для вузов. – 2-е изд.,доп.:-М.:Техносфера,
2005. –393с. 33 экз.
УДК 519.1
2.
Макоха, А.Н. Дискретная математика. Учебное пособие для вузов. –
М.:Физматлит,2005, 368с. 30экз.
УДК 519.1(075.8)
3.
Шапорев,С.Д. математическая логика. Курс лекций и практических
занятий. Учебное пособие для вузов. БХВ – Петербург, 2005.-410с. 59 экз.
УДК 510.6(075.8)
4.
Новиков, Ф. А. Дискретная математика для программистов : Учебное
пособие для вузов / Ф. А. Новиков. - 2-е изд. - СПб. ; М. ; Нижний
Новгород : Питер, 2007. - 363[5] с. : ил. - (Учебник для вузов). [80 экз.]
23

24. Дополнительная литература

1. Галкина,В.Н. Дискретная математика:комбинаторная
оптимизация на графах. –М.:Гелиос АРВ,2003, -232 с.
УДК 519.1(075.8)
2. Нефедов В. Н., Осипова В. А.
Курс дискретной математики. М.,1992.
3. Пападимитру Х., Стайглиц К. Комбинаторная
оптимизация.Алгоритмы и сложность.
М.: Мир,1985, 510 с.
4. Жигалова Е.Ф. Дискретная математика . Учебное
методическое пособие для выполнения лабораторных работ.
Томск, изд-во ТУСУР, 2012, 132 с.
24

25. Благодарю за внимание.

25