Анализ надежности сети логико-вероятностными методами

1. Сети связи

LOGO
Тема № 1:
“ Add your company slogan ”
Анализ и синтез
современных сетей связи по
показателям структурной
устойчивости
Занятие № 8:
Анализ надежности сети логиковероятностными методами
Вид занятия: групповое

2. Цели занятия

2
1. Изучение сущности логиковероятностных методов (ПК-11, ПСК-3.2).
2. Изучение логико-вероятностных
методов (ПК-16).
3. Совершенствование инженерного
мышления (ПСК-3.2).
4. Воспитание чувства ответственности за
качественное обеспечение связи (ОК-4).

3. Межпредметные связи

Основа
Применение
Основы построения
инфокоммуникационных
систем и сетей
Теория телетрафика
Средства и комплексы сетей
связи
Сети связи и системы
коммутации
Сигнализация в сетях связи
3
Сети
связи
Дипломное
проектирование
Учебнопроизводственная
практика

4. Литература

4
1. Рябинин И. А. Логико-вероятностные
методы исследования надежности
структурно-сложных систем / И. А. Рябинин,
Г. Н. Черкесов. – М. : Радио и связь, 1981. –
264 с.
2. Половко А. М. Основы теории
надежности / А. М. Половко, С. В. Гуров. –
2-е изд., перераб. и доп. – СПб. : БХВПетербург, 2006. – 704 с.

5. Учебные вопросы

1
Сущность логико-вероятностных методов
2
Логико-вероятностные методы
5

6. Сущность логико-вероятностных методов

1
Сущность логико-вероятностных
методов
6
Логико-вероятностный
метод
• позволяет формализовать определение и смысл благоприятных гипотез
Состояние каждого i-го
элемента сети связи
• кодируется нулем и единицей.
• исправное состояние i-го элемента сети (графа)
• исправное состояние i-го элемента сети (графа)
1. С помощью функций алгебры логики записывается условие связности сети связи через
работоспособность (состояние) ее элементов. Полученная функция связности сети является двоичной
функцией двоичных аргументов.
2. Полученная функция алгебры логики преобразуется таким образом, чтобы в ней содержались члены,
соответствующие благоприятным гипотезам связности сети.
3. Переход от функции алгебры логики к вероятностной осуществляется по следующим правилам:
•,
(1)
•,
(2)
• операции логического умножения и сложения заменяются операциями арифметического умножения и
сложения.
4. Полученное выражение и есть вероятность связности исследуемой сети связи.

7. Сущность логико-вероятностных методов

1
Сущность логико-вероятностных
методов
Представление функций алгебры логики
табличная форма
в строку (традиционно)
логические матрицы.
Правило формирования логической матрицы
Первоначально функция алгебры логики записывается в строку, определяется
набор конъюнкций функций , составляющих исходную функцию
В матричной форме она представляется в виде строки, элементами
•.
которой являются функции ,
В свою очередь каждая функция представляется в форме дизъюнкций
•.
функций , т. е.
(4)
В матричной форме каждая функция алгебры логики представляется в
виде столбца, элементами которой являются функции , т. е.
•.
(6)
Тогда матричная форма исходной функции алгебры логики имеет вид
•.
(7)
Далее для каждой функции
определяется набор вложенных
конъюнкций и записывается матричная
форма функции алгебры логики
•.
• .(3)
(5)
(8)
Процедура продолжается до тех пор, пока каждая из функций не будет равна какойлибо булевой переменной, т. е. когда
• .
7

8. Сущность логико-вероятностных методов

1
Сущность логико-вероятностных
методов
Функция связности сети связи
Для двухполюсных сетей связи
функцию связности
Для многополюсных –
8
• функция алгебры логики , связывающая состояние элементов
с состоянием сети, данная функция и выражает условия
связности сети.
• можно записать с помощью набора кратчайших путей и
минимальных сечений графа сети
• с помощью набора минимальных остовых деревьев и
минимальных сечений графа сети.
Кратчайший путь
сети
• представляет собой такую конъюнкцию ее элементов (узлов и линий), ни одну из
компонент которой нельзя изъять, не нарушив связность сети:
•,
(9)
• где пробегает все множество номеров, соответствующих данному -му пути.
Минимальное
остовое дерево
• является конъюнкцией его элементов :
•,
(10)
• где пробегает все множество номеров, соответствующих данному -му остовому
дереву.
Минимальное
сечение как
многополюсной,
так и
двухполюсной
сети
• представляет собой такую конъюнкцию из отрицаний ее элементов , ни одну из
компонент которой нельзя изъять, не нарушив условия связности сети:
•.
(11)
• где пробегает все множество номеров, соответствующих данному -му сечению.

9. Сущность логико-вероятностных методов

1
Сущность логико-вероятностных
методов
9
Условия связности двухполюсной сети:
– в виде дизъюнкции всех имеющихся кратчайших
путей
•,
(12)
– в виде конъюнкции отрицаний всех минимальных
сечений
•,
(13)
Условия связности многополюсной сети:
– в виде дизъюнкции всех имеющихся минимальных
остовых деревьев
•,
(14)
– в виде конъюнкции отрицаний всех минимальных
сечений
•,
(15)
Условия связности сети связи можно представить в виде условий работоспособности некоторой
эквивалентной (в смысле надежности) системы, структура которой представляет параллельное
соединение кратчайших путей или минимальных остовых деревьев, или другой эквивалентной
системы, структура которой представляет последовательное соединение отрицаний минимальных
сечений.

10. Сущность логико-вероятностных методов

1
Сущность логико-вероятностных
методов
Задача 1.
• Граф исследуемой сети связи приведен на рисунке. Определить
логическую матрицу связности данной сети в направлении 1–5 и в целом
при условии, что все узлы абсолютно надежны, а ребра ненадежны.
Дано: • .
Найти: • , .
Типовые
состояния
• Простых цепей в графе всего четыре , , , .
• Минимальных сечений в направлении связи 1–5 в графе всего семь , , , , , , .
Функция
связности
сети
•,
Логические
матрицы
•,
•,
10

11. Сущность логико-вероятностных методов

1
Логические матрицы
Типовые
состояния
Функция
связности
сети
• Остовов в графе одиннадцать
•,,,,,,,,,,.
• Сечений в графе одиннадцать
•,,,,,,,,,,.
•,
•.
•,
•,
11

12. Сущность логико-вероятностных методов

1
Правила преобразования логических функций.
Правила логических операций.
Упрощения
конъюнкций
•,
•,
•,
•.
(16)
(17)
(18)
(19)
Упрощения
дизъюнкций
•,
•,
•,
•.
(20)
(21)
(22)
(23)
12
Сочетательный
(или
ассоциативный)
закон:
•,
•,
(24)
(25)
Переместительный
(или
коммутативный)
закон:
•,
•,
(26)
(27)
Правила, выражающие связь между операциями логического умножения и сложения, взятыми
совместно.
Распределительный (или
дистрибутивный) закон
конъюнкции относительно
дизъюнкции:
•,
(28)
Распределительный закон
дизъюнкции относительно
конъюнкции:
•,
(29)

13. Сущность логико-вероятностных методов

1
Закон
двойственности
или
закон
инверсий
Сущность логико-вероятностных
методов
Правила
де
Моргана
•,
•,
•,
•.
Вспомогательные соотношения
Поглощение
•,
(34). (35)
Склеивание
•,
(36)
Поглощение
отрицания
•,
•.
(37)
(38)
Обобщенное
склеивание
•,
(39)
• .(40)
13

14. Выводы

1
Выводы
14
1. Логико-вероятностный метод анализа надежности позволяет формализовать определение и
смысл благоприятных гипотез.
2. Для представления логических уравнений в виде логических матриц конъюнкции
обозначаются расположением логических символов в строке, а дизъюнкции – их
расположением в столбце.
3. Условия связности сети связи можно представить в виде условий работоспособности
некоторой эквивалентной (в смысле надежности) системы, структура которой представляет
параллельное соединение кратчайших путей или минимальных остовых деревьев, или другой
эквивалентной системы, структура которой представляет последовательное соединение
отрицаний минимальных сечений.

15. Логико-вероятностные методы

2
Метод разрезания
• позволяет получить функцию алгебры логики, подставляя в которую вместо логических
переменных вероятности безотказной работы (вероятности отказа) элементов можно
найти вероятность связности сети.
Алгоритм разрезания основан теореме разложения функции алгебры логики
•.
(41)
Принцип упрощения
• если аргумент , функции является совместной двоичной переменной, то, преобразуя
(41), мы переходим к дизъюнкции двух несовместных высказываний, причем в первое
высказывание аргумент входит своим утверждением, а во второе – отрицанием .
Функции и отличаются от функции тем, что в них везде вместо аргумента поставлены
соответственно 1 и 0 (в соответствии с этим выбраны и индексы функций и ).
15

16. Логико-вероятностные методы

2
Логико-вероятностные методы
16
Алгоритм разрезания
1. Подсчитаем число вхождений каждой переменной в
уравнение функции :
•.
(42)
2. Среди чисел находим максимальное и соответствующую
переменную полагаем равной сначала 0, затем 1 и для каждого
случая отдельно выписываем результат подстановки
соответствующей константы в :
•,
•.
(43)
(44)
3. Преобразуем и с помощью правил алгебры логики.
4. После применения указанных преобразований и упрощения функций и может оказаться, что любая
из них либо превращается в константу, либо принимает такой вид, при котором каждая из оставшихся
переменных будет входить в выражение не более одного раза или при котором хотя бы одна из
переменных входит в выражение функции более одного раза.
5. Если имеет место третий случай, то для
соответствующей функции опять вычислим - для
всех оставшихся в явном виде переменных и
опять произведем разрезание функции по
переменной, соответствующей максимуму .
• если разрезанию подвергалась функция
•,
(45)
•.
(46)
• если разрезанию подвергалась функция
•,
(47)
•.
(48)
К полученной таким образом системе функций применим преобразования логических функций, а затем
выполним действия, указанные в пп. 4 и 5 до тех пор, пока на очередном шаге не окажется, что ни для
одной функции не имеет места третий случай, указанный в п. 4.

17. Логико-вероятностные методы

2
Логико-вероятностные методы
Задача 2.
• Граф исследуемой сети связи приведен на рисунке. Все узлы сети
являются абсолютно надежными, а вероятность исправности любой линий
связи равна 0,9. Определить надежность сети связи в целом и в
направлении 1–5 методом разрезания.
Дано: • .
Найти: • , .
Функция связности, полученная на основе сечений
•.
17

18. Логико-вероятностные методы

2
Логико-вероятностные методы
18

19. Логико-вероятностные методы

2
Логико-вероятностные методы
Вeроятность
связности
• ).
19

20. Логико-вероятностные методы

2
Логико-вероятностные методы
Функция
связности,
полученная
на основе
остовых
деревьев
•.
20

21. Логико-вероятностные методы

2
Логико-вероятностные методы
21

22. Логико-вероятностные методы

2
Логико-вероятностные методы
=
Вeроятность
связности
22

23. Логико-вероятностные методы

2
Логико-вероятностные методы
Метод
ортогонализации
23
• основан на преобразовании произвольной функции алгебры логики в
ортогональную дизъюнктивную нормальную форму.
Утверждение 1.
• Отрицание элементарной конъюнкции ранга эквивалентно дизъюнкции ,
члены которой попарно ортогональны.
•.
(49)
Утверждение 2.
• Булева функция, представленная в дизъюнктивной нормальной форме в виде ,
эквивалентна функции .
•.
(50)

24. Логико-вероятностные методы

2
Логико-вероятностные методы
24
Алгоритм преобразования логической функции к ортогональной дизъюнктивной нормальной форме:
1. Преобразуем сначала логическую функцию к дизъюнктивной нормальной форме.
2. Произведем нумерацию членов дизъюнктивной нормальной формы от 1 до , причем членам низшего
ранга присвоим меньшие номера.
3. Определим ортогональную дизъюнктивную нормальную форму логической функции с помощью
преобразований (49) или (50).
Для уменьшения количества операций в конъюнкциях целесообразно выполнить следующие
упрощения:
• – приравнять нулю те члены дизъюнктивной нормальной формы , , которые ортогональны члену ,
• – приравнять нулю те элементарные конъюнкции отрицаний , , которые ортогональны .
4. Преобразовав условия работоспособности системы к ортогональной дизъюнктивной нормальной
форме, можно приступить к вычислению вероятности безотказной работы системы.

25. Логико-вероятностные методы

2
Логико-вероятностные методы
Задача 3.
• Граф исследуемой сети связи приведен на рисунке 1. Все узлы сети
являются абсолютно надежными, а вероятность исправности любой линий
связи равна 0,9. Определить надежность сети связи в целом и в
направлении 1–5 методом ортогонализации.
•,.
Дано:
Найти:
•,.
Функция связности,
полученная на
основе простых
цепей
•.
Члены функции
•.
Отрицания
конъюнкций
•,
25

26. Логико-вероятностные методы

2
Логико-вероятностные методы
,
26

27. Логико-вероятностные методы

2
Логико-вероятностные методы
,
27

28. Логико-вероятностные методы

2
Логико-вероятностные методы
Ортогональная
дизъюнктивная
форма
Вероятность
связности
28

29. Логико-вероятностные методы

2
Функция
Члены отрицания функции связности
связности,
•.
полученная на
основе сечений
Отрицание
Члены отрицания функции связности
функции
связности
Члены функции связности
•.
•.
•.
Члены функции связности
•.
•.
29

30. Логико-вероятностные методы

2
Логико-вероятностные методы
30

31. Логико-вероятностные методы

2
Логико-вероятностные методы
31

32. Логико-вероятностные методы

2
Логико-вероятностные методы
32

33. Логико-вероятностные методы

2
Логико-вероятностные методы
33

34. Логико-вероятностные методы

2
`
Логико-вероятностные методы
34

35. Логико-вероятностные методы

2
Логико-вероятностные методы
Ортогональная дизъюнктивная форма
•.
Вероятность связности
• ((
35

36. Логико-вероятностные методы

2
Логико-вероятностные методы
36
Схемно-логический
метод
• основан на обобщенной теореме разложения произвольной функции
алгебры логики по любым аргументам и использовании логической схемы (в
литературе используется термин релейно-контактная схема), являющейся
наглядной графической моделью условий связности исследуемой сети
связи.
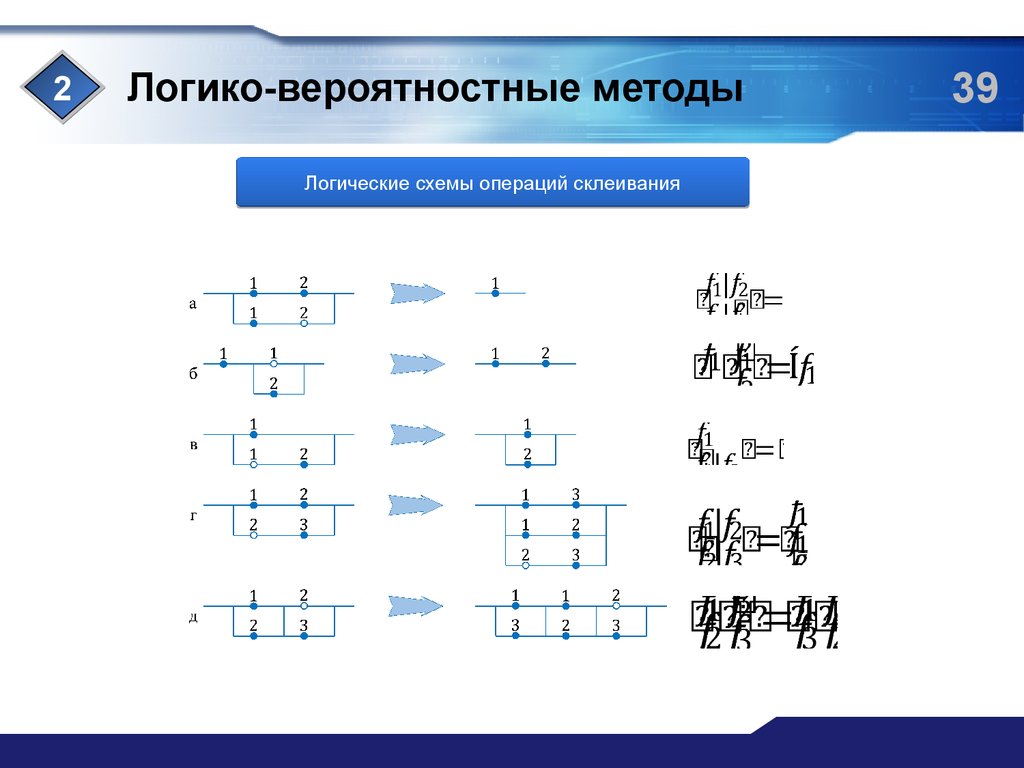
На логической схеме
каждый элемент сети
связи
• изображается кружком, а связи между ними, заменяют логические операции
конъюнкции и дизъюнкции. При таком изображении логическая схема всегда
получается в виде последовательно-параллельных цепей (а не мостиковых
структур) с многими повторяющимися кружками.
Логическая схема
• дает наглядное представление о комбинации "выгодных" переменных, по
которым следует делать разложение функции алгебры логики, и о наиболее
целесообразной последовательности преобразований, которая приводит
схему к простейшему виду.
Элементы сети связи
на логических схемах
изображаются
кружками,
• причем закрашенный кружок идентифицирует соответствующую логическую
переменную, а незакрашенный – ее отрицание.

37. Логико-вероятностные методы

2
Логико-вероятностные методы
Логические схемы упрощения конъюнкций
37
Логические схемы упрощения дизъюнкций
Логические схемы переместительного
(коммутативного) закона
Логические схемы сочетательного (ассоциативного) закона

38. Логико-вероятностные методы

2
Логико-вероятностные методы
Логические схемы распределительных
(дистрибутивных) законов
Логические схемы операций поглощения
38

39. Логико-вероятностные методы

2
Логико-вероятностные методы
Логические схемы операций склеивания
39

40. Логико-вероятностные методы

2
Логико-вероятностные методы
40
Алгоритм схемно-логического метода
1. По условиям связности сети связи, записанным в дизъюнктивной нормальной форме, изображается
логическая схема.
2. Выбирается для вынесения в последовательную цепь такую комбинацию элементов, которая
обеспечивает размыкание всех или большей части параллельных цепей логической схемы. После
вынесения группы из элементов логическая схема распадается на параллельных схем.
3. В каждой из полученных параллельных схем производятся преобразования, вытекающие из теоремы
разложения: закрашенные кружки, одинаковые с вынесенными элементами, преобразуются замыкание
цепи, а незакрашенные кружки – в размыкания цепи.
4. В схемах, полученных в результате преобразований, удаляются все разомкнутые цепи и заменяются
все группы элементов, оказавшиеся короткозамкнутыми проводом (линией). Кроме того, элементы,
имеющиеся во всех параллельных цепях, выносятся в общую последовательную цепь, а цепи,
поглощаемые другими параллельными им цепями, удаляются.
5. Изучается каждая из последовательных схем: если схема постоянно разомкнута, то она из
дальнейшего рассмотрения исключается; если схема постоянно замкнута, то она дальнейшим
преобразованиям не подвергается; если схема бесповторная, то на этом процесс ее преобразования
также заканчивается. Бесповторная функция, соответствующая данной схеме, записывается в
конъюнктивной форме. В случае небесповторных схем осуществляется возврат к п. 2 и производятся
дальнейшие преобразования в соответствии с пп. 2–5.
6. По полученным в результате преобразований схемам записывается функция алгебры логики.
7. От функции алгебры логики осуществляется переход к вероятностной функции и по ней вычисляется
вероятность связности сети связи как вероятность равенства функция алгебры логики единице.

41. Логико-вероятностные методы

2
Логико-вероятностные методы
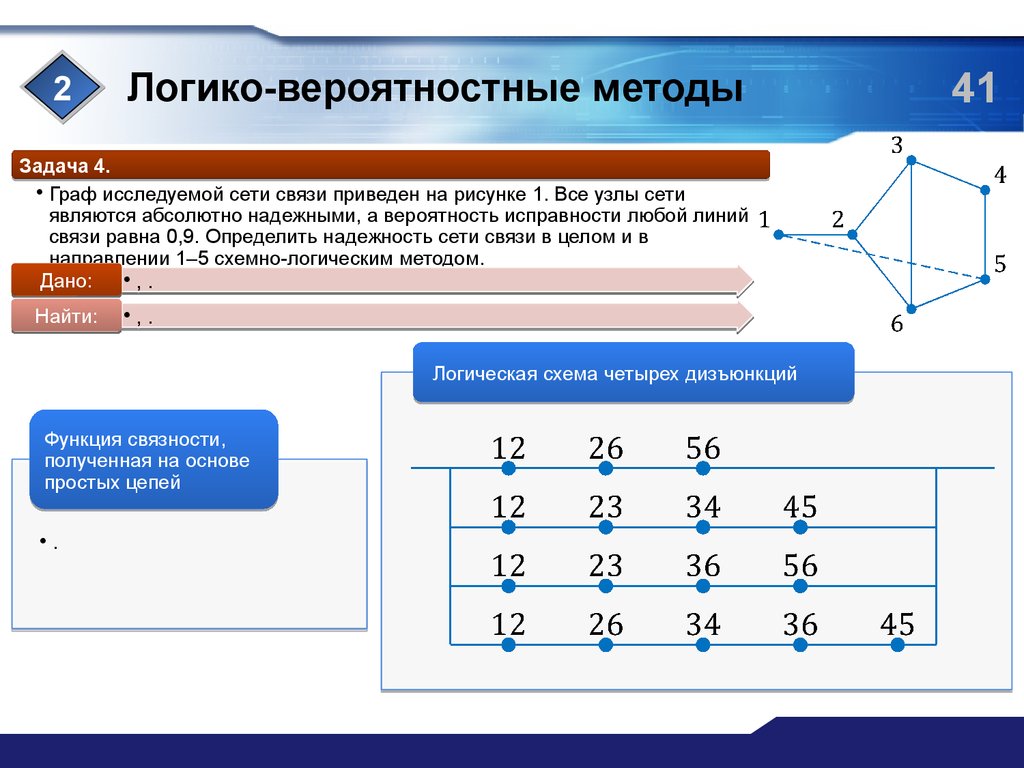
Задача 4.
• Граф исследуемой сети связи приведен на рисунке 1. Все узлы сети
являются абсолютно надежными, а вероятность исправности любой линий
связи равна 0,9. Определить надежность сети связи в целом и в
направлении 1–5 схемно-логическим методом.
•,.
Дано:
Найти:
•,.
Логическая схема четырех дизъюнкций
Функция связности,
полученная на основе
простых цепей
•.
41

42. Логико-вероятностные методы

2
Логико-вероятностные методы
Применение дистрибутивного
закона конъюнкции
относительно дизъюнкции по
ребру 12.
Использование
дистрибутивного закона
конъюнкции относительно
дизъюнкции по ребрам 23 и 26.
Разложим логическую
схему относительно
ребра 56
Упростим полученные
конъюнкции и
дизъюнкции
42

43. Логико-вероятностные методы

2
Логико-вероятностные методы
43
Используем дистрибутивный закон
конъюнкции относительно дизъюнкции по
ребрам 34 и 45.
Разложим логическую схему сначала
относительно ребра 23
Упростим полученные конъюнкции и
дизъюнкции.

44. Логико-вероятностные методы

2
Логико-вероятностные методы
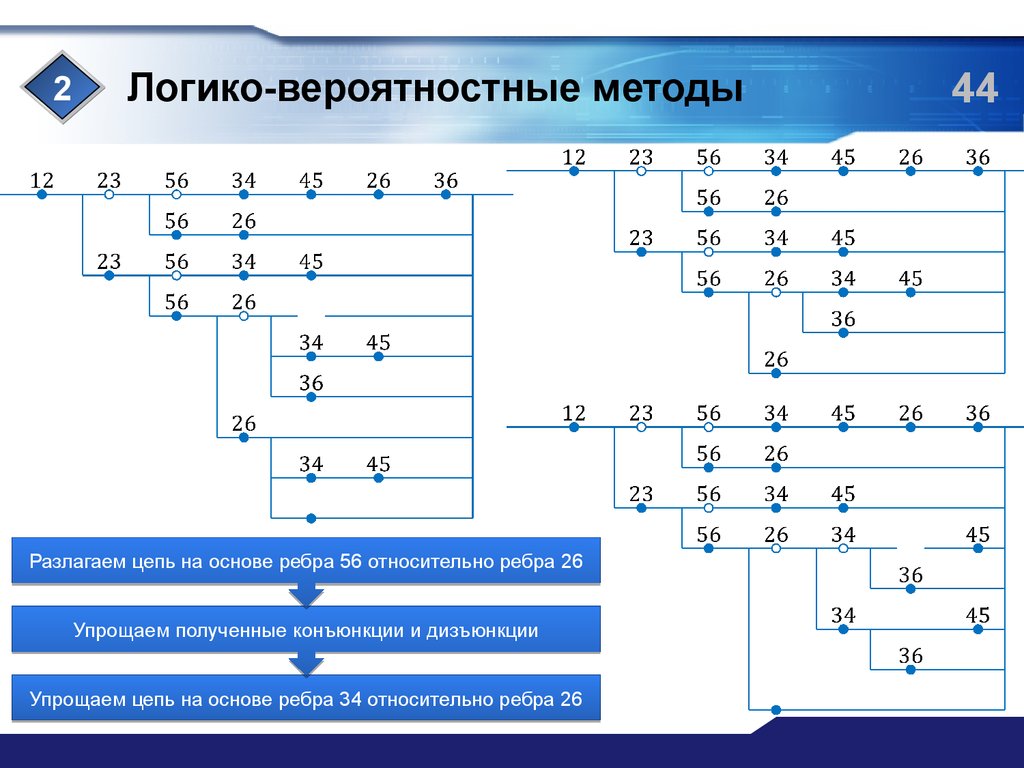
Разлагаем цепь на основе ребра 56 относительно ребра 26
Упрощаем полученные конъюнкции и дизъюнкции
Упрощаем цепь на основе ребра 34 относительно ребра 26
44

45. Логико-вероятностные методы

2
Логико-вероятностные методы
45
Упрощаем полученные конъюнкции и дизъюнкции
Упрощаем цепь на основе ребра 34 относительно
ребра 36
Упрощаем полученные конъюнкции и дизъюнкции

46. Логико-вероятностные методы

2
Задача 4.
• Граф исследуемой сети связи приведен на рисунке 1. Все узлы сети
являются абсолютно надежными, а вероятность исправности любой линий
связи равна 0,9. Определить надежность сети связи в целом и в
направлении 1–5 схемно-логическим методом.
•,.
Дано:
Найти:
•,.
Функция связности, полученная на основе сечений
•.
Логическая схема одиннадцати конъюнкций
46

47. Логико-вероятностные методы

2
Логико-вероятностные методы
47
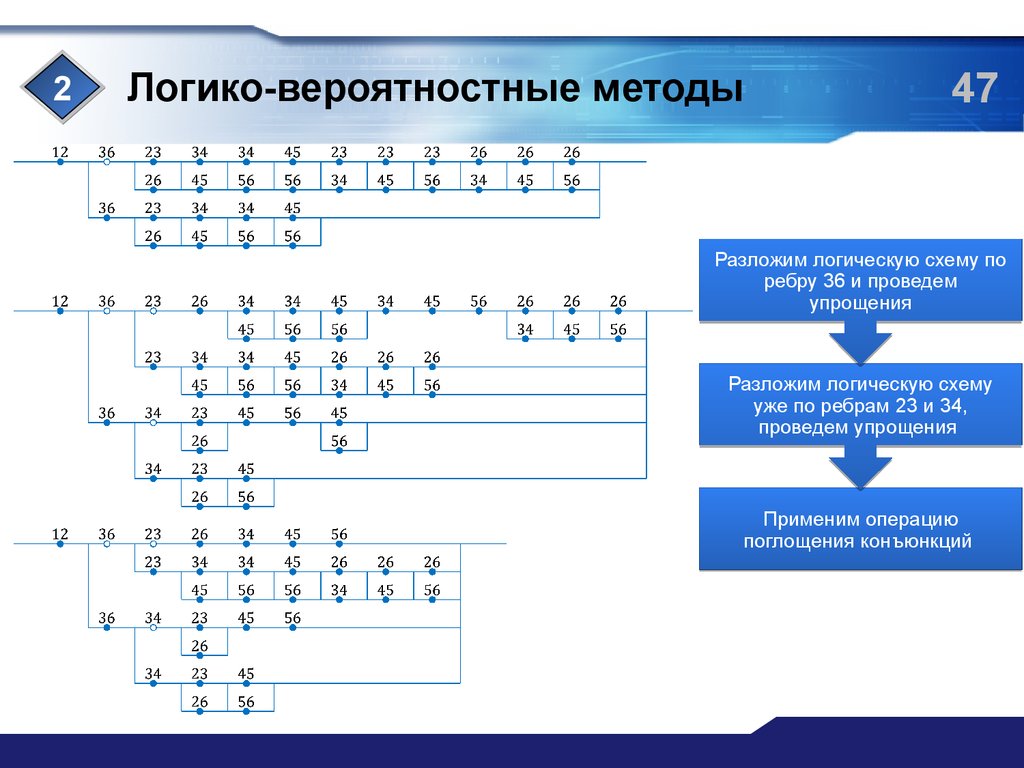
Разложим логическую схему по
ребру 36 и проведем
упрощения
Разложим логическую схему
уже по ребрам 23 и 34,
проведем упрощения
Применим операцию
поглощения конъюнкций

48. Логико-вероятностные методы

2
Логико-вероятностные методы
48
Разложим логическую схему по
ребрам 26 и 23 и проведем
упрощения
Применим операцию
поглощения конъюнкций

49. Логико-вероятностные методы

2
Логико-вероятностные методы
Разложим логическую схему по
ребрам 34 и 45, проведем
упрощения
Разложим логическую схему по
ребру по ребру 45
49

50. Выводы

2
Выводы
50
1. Метод разрезания позволяет получить функцию алгебры логики,
подставляя в которую вместо логических переменных вероятности
безотказной работы (вероятности отказа) элементов можно найти
вероятность связности сети.
2. В некоторых случаях переход от повторной функции алгебры логики к
вероятностной форме удобнее реализовать (например, с помощью
процессоров) не по формуле полной вероятности, а с помощью теоремы
сложения вероятностей несовместных событий.
3. Использование схемно-логического метода преобразования функции
алгебры логики для расчета надежности сетей позволяет найти вероятность
связности значительно быстрее, чем применение вышеизложенных
методов.

51. Литература

51
1. Рябинин И. А. Логико-вероятностные
методы исследования надежности
структурно-сложных систем / И. А. Рябинин,
Г. Н. Черкесов. – М. : Радио и связь, 1981. –
264 с.
2. Половко А. М. Основы теории
надежности / А. М. Половко, С. В. Гуров. –
2-е изд., перераб. и доп. – СПб. : БХВПетербург, 2006. – 704 с.

52. Сети связи

LOGO
Тема № 1:
“ Add your company slogan ”
Анализ и синтез
современных сетей связи по
показателям структурной
устойчивости
Занятие № 8:
Анализ надежности сети логиковероятностными методами
Вид занятия: групповое

53. Цели занятия

53
1. Изучение сущности логиковероятностных методов (ПК-11, ПСК-3.2).
2. Изучение логико-вероятностных
методов (ПК-16).
3. Совершенствование инженерного
мышления (ПСК-3.2).
4. Воспитание чувства ответственности за
качественное обеспечение связи (ОК-4).